惯用坐标表示基本事件
2018-06-01郑瑞
郑 瑞
(江苏省灌南县第二中学 222500)
在学习必修三《概率》一章中,求古典概型和几何概型的概率很重要的一步是列举基本事件与寻找区域D、d,但在具体列举基本事件与寻找区域D、d时,很多同学颇感头痛,稍有疏忽,就给个“小”教训.如何刻画基本事件呢?坐标法表示基本事件,苏教版必修三中并没有详细展开.很多同学做这方面题目时依然使用初中的一些方法,比如树状图、列表等,这些方法虽然可以,但是不宜于描述与书写,没有与函数等联系起来,做高中题目就要多使用高中的方法.孰能生巧,习惯用用坐标表示基本事件这样才有利于后续概率知识的展开.下面举例说明它的应用.
例1 一只口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出2只球.
(1)共有多少基本事件?
(2)摸出的2只球都是白球的概率是多少?
解(1)分别记白球1,2,3号,黑球为4,5号,从中摸出2只球,有如下基本事件[摸到1,2号球用(1,2)表示]:
(1,2)(1,3)(1,4)(1,5)
(2,3)(2,4)(2,5)
(3,4)(3,5)
(4,5)
因此,共有10个基本事件.

例2 一只口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出2只球.
每次摸1个球,连续摸两次.
(1)共有多少基本事件?
(2)摸出的两只球都是白球的概率是多少?
解(1)分别记白球1,2,3号,黑球为4,5号,从中摸出2只球,每次摸1个球,连续摸两次.有如下基本事件[摸到1,2号球用(1,2)表示]:
(1,2)(1,3)(1,4)(1,5)
(2, 1)(2,3)(2,4)(2,5)
(3, 1)(3,2)(3,4)(3,5)
(4,1)(4,2)(4,3)(4,5)
(5,1)(5,2)(5,3)(5,4)
因此,共有20个基本事件.
(2)记摸到2只白球的事件为事件A,
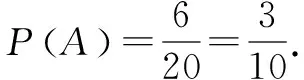
例3 一只口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出2只球.
每次摸1个球,摸后放回,连续摸两次.
(1)共有多少基本事件?
(2)摸出的两只球都是白球的概率是多少?
解(1)分别记白球1,2,3号,黑球为4,5号,从中摸出2只球,每次摸1个球,摸后放回,连续摸两次.有如下基本事件[摸到1,2号球用(1,2)表示]:
(1,1)(1,2)(1,3)(1,4)(1,5)
(2, 1)(2, 2)(2,3)(2,4)(2,5)
(3, 1)(3,2)(3,3)(3,4)(3,5)
(4,1)(4,2)(4,3)(4,4)(4,5)
(5,1)(5,2)(5,3)(5,4)(5,5)
因此,共有25个基本事件.
(2)记摸到2只白球的事件为事件A,
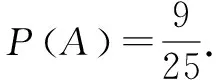
小结在用坐标列举古典概型的基本事件时,要注意有无顺序,有无放回.没有顺序时,(x,y)与(y,x)表示同一个基本事件,例1中(1,2)与(2, 1)是同一个基本事件,因此只写了前一个;有顺序时,(x,y)与(y,x)表示两个不同的基本事件,例2中(1,2)与(2, 1)是两个不同基本事件,因此两个都要列举;没有放回时,无(x,x)这个“基本事件”,例1与例2中都没有形如(1,1)这样的“基本事件”;有放回时,有(x,x)这个基本事件,例3中有形如(1,1)这样的基本事件5个.用坐标列举时要做到不重复、不遗漏.
例4 某厂生产的10件产品中,有8件合格品,2件不合格品,合格品与不合格品在外观上没有区别.从这10件产品中任意抽检2件,计算:(1)共有多少基本事件;(2)2件都是合格品的概率.
解(1)记8件合格品为1,2,3,…,7,8,记2件不合格品为9,10.从这10件产品中任意抽检2件,如下基本事件:
(1,2)(1,3)…(1,9)(1,10)
(2, 1)(2,3)…(2,10)
⋮
(8,9)(8,10)
(9,10)
因此,共有1+2+3+…+9=45个基本事件.
(2)记抽检2件都是合格品的事件为事件A,

小结对于基本事件数目较多,可用省略号表示类似的基本事件.
例5 甲、乙二人约定在0点到 5 点之间在某地会面,先到者等一个小时后即离去,设二人在这段时间内的各时刻到达是等可能的,且二人互不影响.求二人能会面的概率.
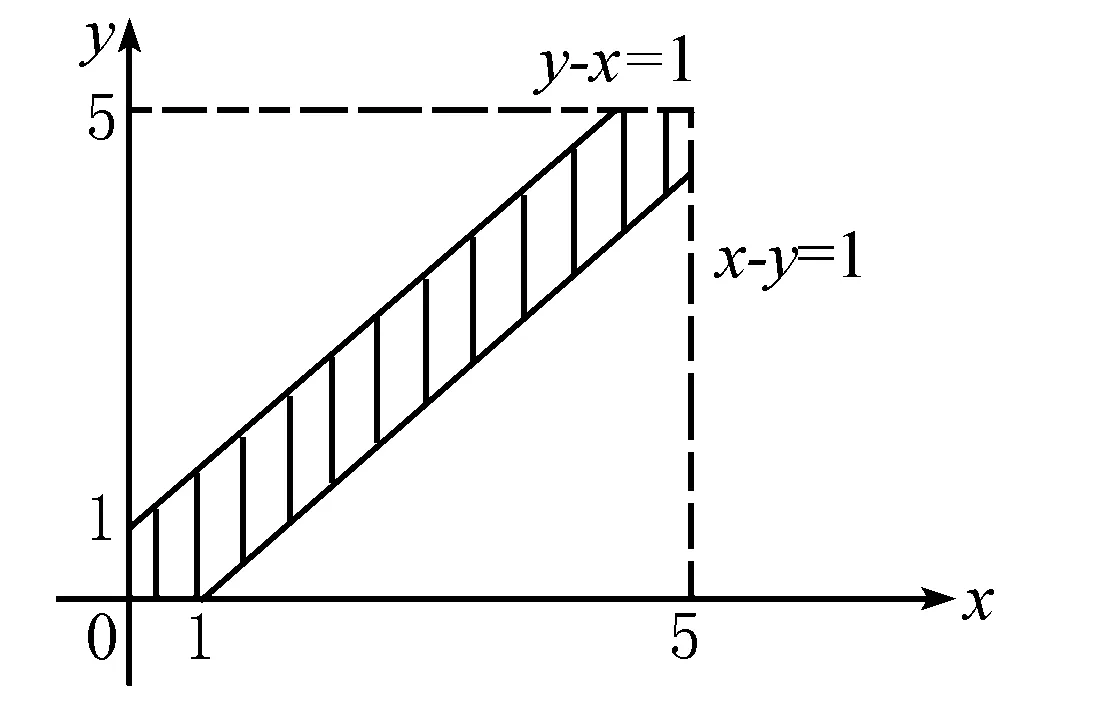

小结对于此类问题,关键是建立数学模型,建立适当的坐标系,找到所需的线性约束条件,从而转化为面积型几何概型问题.
与概率计算密切相关的“计数问题”要到选修模块的系列2中学习,许多同学没有机会学到,无法用排列组合的方法来研究相关概率问题.习惯用坐标表示基本事件,就显得更重要,这样就与解析几何、函数与方程等同学们熟悉的内容结合起来,容易接受掌握.坐标法尤其适用选两个的情况,选三个或三个以上时就不大方便了.
参考文献:
[1]于志华.几何概型中概率的计算[J].中国教育与教学,2007(3):5.
[2]尤承业.解析几何[M].北京:北京大学出版社,2004.
