伪码信号辅助的CEI载波时延模糊度解算*
2018-05-29
(航天工程大学 光电装备系,北京 101416)
1 引 言
连线干涉测量(Connected Elements Interferometry,CEI)系统[1]通过相距几百米到上百公里的两测站间使用光纤传递时标和频标,能够极大地消除地面甚长基线干涉测量(Very Long Baseline Interferometry,VLBI)网站有关的误差项,如时钟同步误差、信号传播延迟和仪器误差等,从而获得高精度的方向信息,具有基线短、布站灵活、测角精度高、实时性好等优点。相位模糊度解算是CEI测量的难点之一[2],而且基线越长,模糊度解算越困难。干涉测量中常用的解模糊方法主要有ΔDOR法[3]、相位参考法[4]、频率综合法[5]以及地球自转综合法[6],其中ΔDOR法和频率综合法应用较为广泛。ΔDOR法通过解算DOR信号的群时延而非载波时延实现测量,由于受信道带宽的限制,测量精度有限[7]。频率综合法利用多个频率信号的群时延辅助解算载波时延模糊度[8-9],对群时延精度要求较高,而且利用信号形式较多。地球自转综合法利用相对目标的有效基线长度随着地球自转而发生变化,使单一基线可等效为长度、方向均不同的一组基线,从而实现载波差分相位解模糊,但是该方法需要较长的观测时间,对系统设备的相位抖动性能和信道误差的影响提出了较高要求,鲁棒性较差。总的来说,先验模型的精度决定了解模糊的能力和方法,而这主要取决于轨道预报的精度,在无轨道预报或轨道预报精度不高时,解算能力低甚至难以进行正确的解算。伪码测距是利用伪随机序列的自相关性获取接收伪码与伪本地码的偏移量来计算信号传输时延,进而得到目标与测站间距离的测距方式[10-11]。在深空伪码测距应用中,码长1 023,码速率5 Mchip/s,载噪比50 dBHz,可以实现精度1 m以内的测距,对应的时延测量精度为3 ns。通过提高伪码周期可以增大无模糊距离[12],而提高码速率、减小码片宽度可以提高测量分辨率,进一步提高测距精度。
伪码的捕获和跟踪是伪码测距精度的主要决定因素,提高捕获概率、效率及跟踪精度是伪码测距所需解决的主要问题[13-15]。结合CEI基线较短的特点,针对具有伪码测距能力的测站,本文提出了一种利用伪码测距信号辅助的CEI高精度时延解模糊方法,通过距离约束,设计合理的伪码测距信号参数,计算两测站接收测距伪码信号的相对偏移量作为高精度时延预报值。仿真证明,所提方法在低信噪比下具有宽带群时延的解模糊能力,在信噪比较高时,具有S频段载波时延的解模糊能力。
2 CEI时延解算及整周模糊度分析
设频率为f的信号到达两测站的时延差为Δτ,则有
2πfΔτ=2πN0+φ。
(1)
式中:φ∈[-π,π]为相关相位的观测值;当Δτ>1/f时,N0≥1,此时便产生了相位模糊。因此,想要得到准确的时延差,必须解出相位模糊度N0。
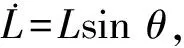
(2)
则要求
(3)
当λ≈13 cm时,δR≤46.8/sinθ;当λ≈3 cm时,δR≤10.8/sinθ。为了确保不会产生相位模糊,在S和X频段,δR的最大值分别为46.8和10.8。若考虑其他误差因素的影响,对δR的要求会更高。地球同步轨道(Geosynchronous Earth Orbit,GEO)卫星中导航星的初始轨道精度一般在100 m左右,而中继卫星的初始轨道精度约为1 km[2]。因此,对于基线长度50 km以上的CEI测量系统,在现有轨道预报精度下获取的时延预报值,无论是S频段还是X频段都会产生相位整周模糊。
3 基于伪码测距信号辅助的CEI载波相位时延解模糊方案
3.1 不同长度基线无模糊条件
假设目标到两测站符合远场测量条件,入射波束为平行光,其模型如图1所示。其中,ΔD表示信号到两测站的距离差,根据直角三角形的特点,满足ΔD
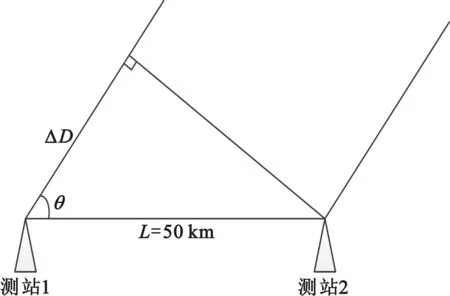
图1 CEI模型图Fig.1 Model of CEI
伪码周期由码长和码片宽度决定:
Tc=N·tc=N/Rc。
(4)
式中:N代表伪码长度,Rc代表伪码速率。因此,只要满足N/Rc>L/C就能够保证接收伪码无周期模糊。 在基线长度一定的条件下,为了提高伪码周期,可以提高码长或者降低码速率,但是随着码速率的降低,码片宽度增大,测量精度便会随之降低,因此,采用高码速率的长码是较理想的实现方式。
本文以基线长度L=50 km为例进行讨论,则Δτ=ΔD/C≈0.000 167 s。
长码往往伴随着长的捕获时间。在深空伪码测距中,为了快速捕获,一般采用复合码。长度分别为m、n的两个伪码序列可以复合出长度为m·n的复合码,捕获时间为tm+tn,而同等长度的单码捕获时间为tm·tn,复合码在保持了自相关性的同时大大缩短了捕获时间。
3.2 基于伪码测距信号辅助的CEI高精度时延解算
图2是两测站接收的伪码信号可能处于不同伪码周期的位置示意图。图2(a)表示两站接收的伪码信号处于相邻周期,由于Δτ

图2 两测站接收伪码位置示意图
Fig.2 Position diagram of the received PN codes
伪码捕获的主要功能是使接收伪码与本地伪码粗对齐,成功捕获后误差在一个码片宽度范围内,而伪码跟踪则是获取接收伪码相对于本地伪码不足一个码片的偏移量,是决定测距精度的根本环节。伪码跟踪一般采用基带相关同步跟踪回路和包络相关同步跟踪回路,其最主要的区别是基带相关同步跟踪回路的接收信号在扩频码同步跟踪之前已经被解调,而包络相关同步跟踪回路的输入信号是接收的扩频信号。基带相关同步跟踪回路存在的主要问题是低信噪比条件下,在未对扩频信号解扩的条件下完成解调是十分困难的,同时,它忽略了信息信号的存在。因此,本文采用包络相关的同步跟踪环路[15]对伪码进行跟踪。
热噪声引起的环路跟踪误差为[14]
(5)
式中:σDLL为码跟踪环路的均方根误差(单位:chip),BL为环路等效带宽(单位:Hz),TI为相关积分时间,C/N0为信号载噪比,d为相关间隔。
捕获跟踪过程完成后,便可以计算得到一个时延初值。多次仿真实验证明,在信噪比较高时其精度可以满足S频段无模糊相位时延要求,但是在信噪比较低时,不满足要求。此时,引入群时延来辅助相位时延的求解[8]。相时延和群时延是针对信号形式和时延求解条件的差异而采用的不同求解方法,其特点如表1所示。

表1 载波时延和群时延特点Tab.1 Characteristic of carrier delay and group delay
表1中,φ表示载波相位,fRF表示射频载波频率,f1、f2分别为群时延计算带宽的起始频率,φ1、φ2分别为f1、f2频点的相位,σφ为相位提取误差。
总的实现过程如图3所示。依据初始时延的估计精度,采用逐步求解相位模糊的方法,先计算宽带群时延再依次求解S频段甚至X频段无模糊载波相位时延。
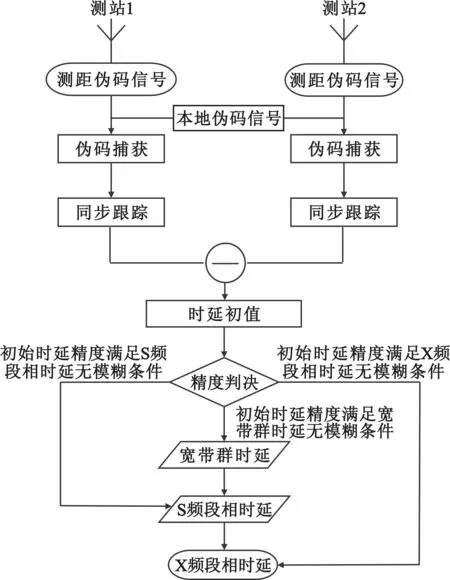
图3 基于测距伪码信号辅助的CEI 载波时延提取流程图Fig.3 Flow chart of CEI carrier delay extraction aided by PN code ranging signals
4 仿真实验
4.1 仿真条件
设基线长50 km,结合复合码的产生原则和时延测量精度要求,选用长度分别为127和63的m序列产生长度为8 001的复合码,伪码速率设置为Rc=20.002 5 Mchip/s,码片宽度tc=1/Rc≈50 ns,码周期Tc=N/Rc=8 001/(20.002 5×106)=4×10-4s>2Δτ,对应最大无模糊距离为120 km;信息速率为2.5 kbit/s,中频频率320 MHz,中频采样率0.800 1 GHz;信噪比范围为-30~15 dB。设信号到达两测站的时间位于同一码片周期,到达测站1的不足一个整周期位置为第532.345码片,到达测站2的不足一个整周期位置为第114.728码片,则信号到达两测站的时延差为
(532.345-114.728)×49.993 75=20 878.239 893 75 ns 。
(6)
4.2 伪码捕获、跟踪
假设多普勒频率已完全补偿,信噪比是伪码捕获性能的主要影响因素,信噪比越高则捕获概率越高,为了验证算法有效性,本文只在最低信噪比条件下对伪码进行捕获,捕获方法为传统滑动相关法。信噪比为-30 dB时,两测站伪码捕获结果如图4所示。
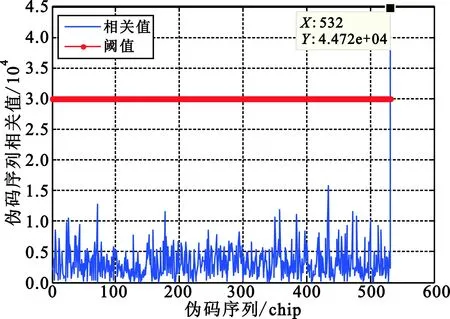
(a)测站1伪码捕获结果
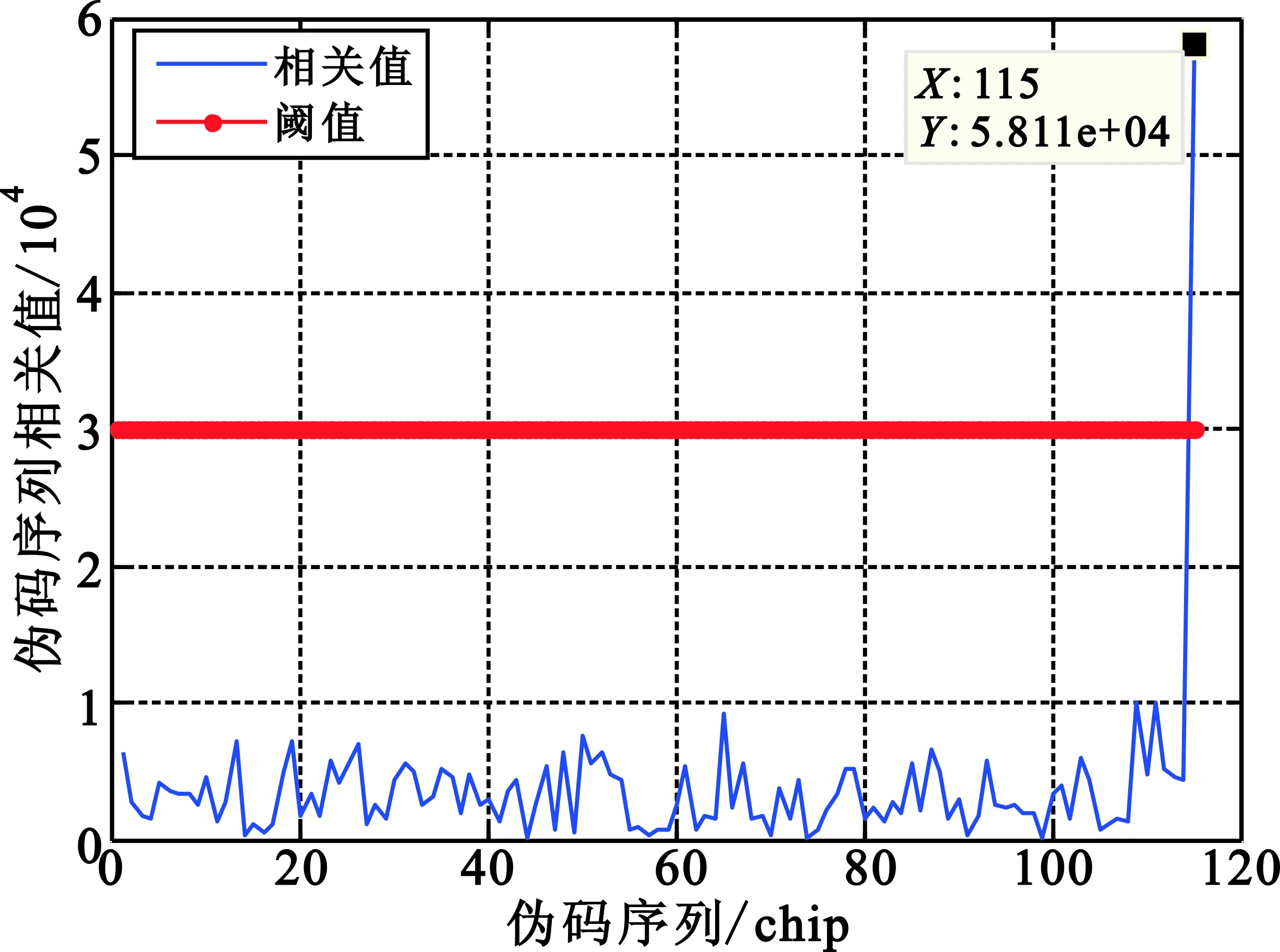
(b)测站2伪码捕获结果图4 两测站伪码捕获结果Fig.4 PN code capture results of two stations
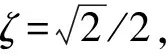
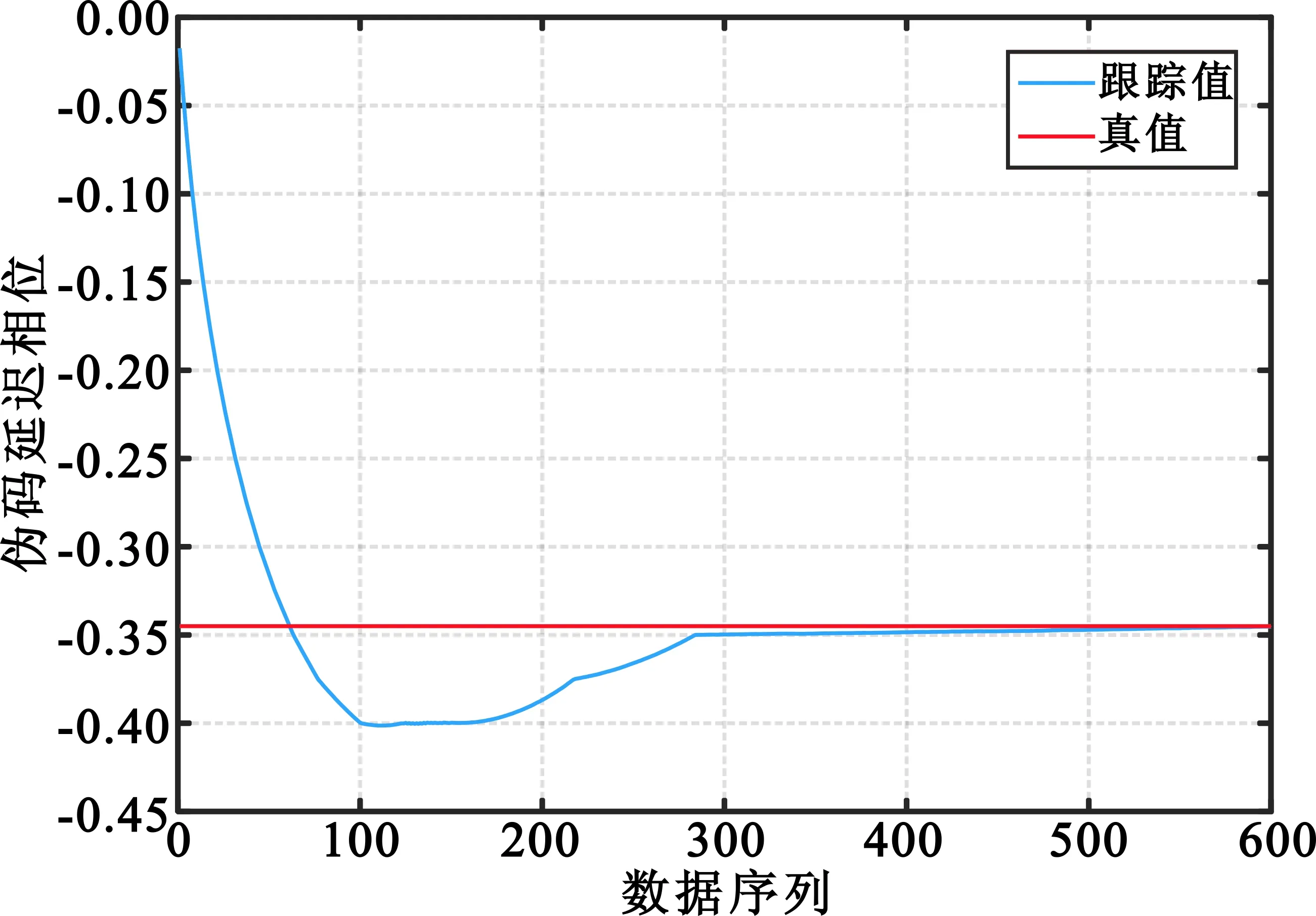
(a)测站1伪码跟踪结果
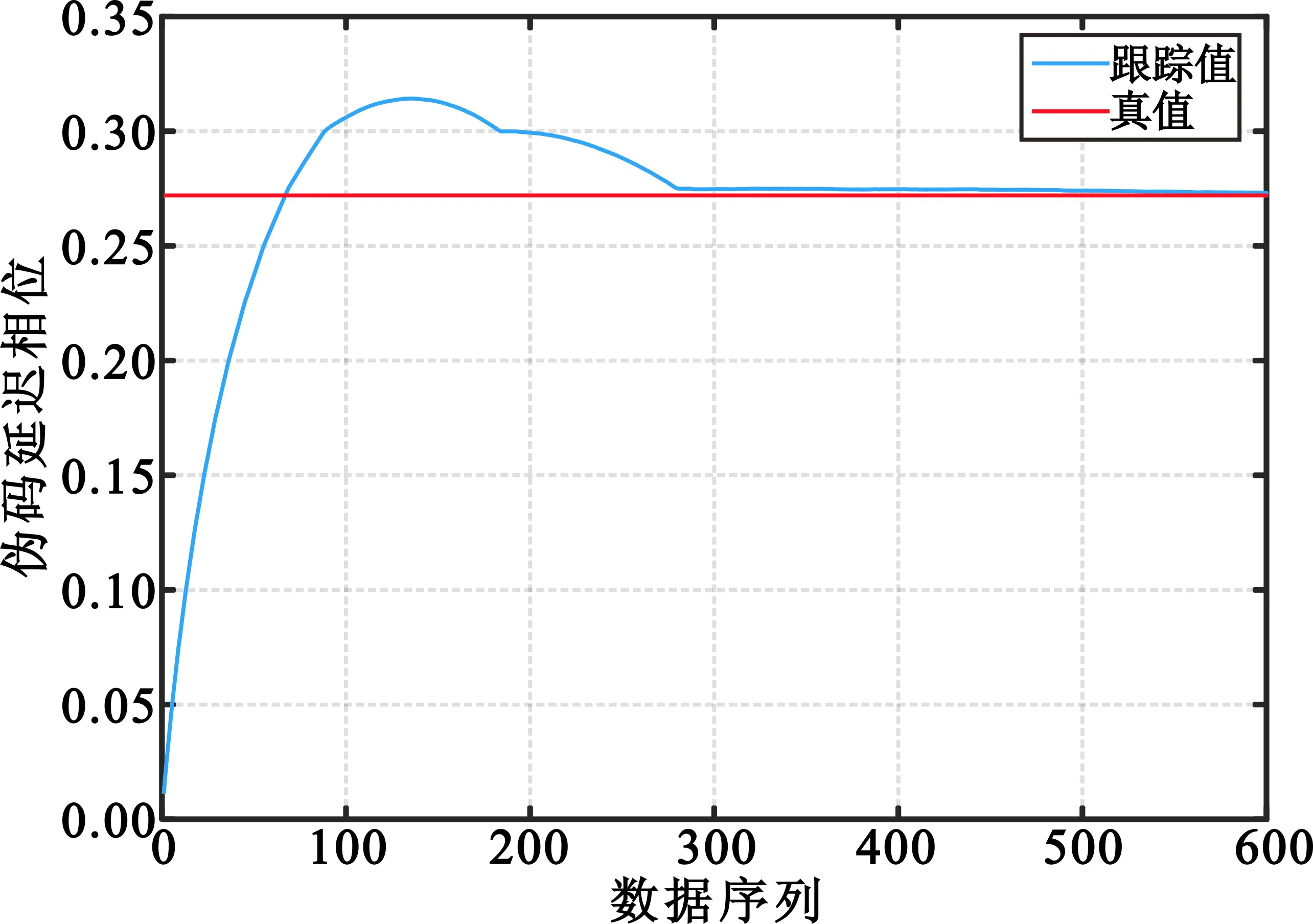
(b)测站2伪码跟踪结果图5 信噪比为0 dB时两测站伪码跟踪结果Fig.5 PN code tracking results of two stations when SNR=0 dB
对不同信噪比条件下跟踪结果进行误差分析,通过1 000次蒙特卡洛实验,在跟踪环路达到稳态后,得到测站1跟踪结果的均方根误差如图6所示。

图6 不同信噪比下的跟踪误差Fig.6 Tracking errors in different signal-to-noise ratio
由于噪声的影响,误差具有波动性,在此引入概率论中的3σ准则[8],其表达式为
P{|x-α|≤3σ}≈99.7% 。
(7)
式中:x表示统计量,α表示真值,σ表示均方根误差。因此,为了确保能够正确解出载波相位模糊度,必须满足
(8)
σT表示两站在同步跟踪环节的总误差。由公式(5)可知,在其他参数保持一致时跟踪精度主要由信噪比决定,由于两站距离较近,在接收设备相同时,可近似认为接收信号的信噪比相等,因此两站跟踪过程中所产生的误差相等。此时,类似于表1中的群时延误差,有
(9)
结合公式(8),对单站的跟踪误差σDLL要求为
(10)
以航天测控中S频段为例,载波频率fRF=2.2 GHz,本文中Rc=20.002 5 MHz,计算得到σDLL<0.001 1。由图8可以看出,在信噪比大于等于0 dB时,可以满足S频段计算无模糊载波相位时延的要求;而信噪比小于0 dB时,虽然不满足计算无模糊载波相位时延的要求,但是可以满足宽带群时延无相位模糊。群时延解相位模糊对单站跟踪误差σDLL要求为
(11)
Bgroup为群时延的计算带宽。在信噪比为-30 dB时,σDLL≈0.016,代入式(8)和式(9)中有Bgroup<147 MHz。在传统干涉测量中,为了提高测量精度,通常需要提高测量信号带宽,一般采用逐级解模糊的方法,先计算较窄带群时延再依次解宽带群时延的相位模糊,需要多次处理,而本文方法可直接实现最大带宽为147 MHz的无模糊群时延计算。
4.3 性能分析
取跟踪过程稳定后的平均值为小数码元偏移量,结合捕获结果得到初始时延值,与真实值之差的绝对值作为误差。在-30 dB和0 dB两个典型的信噪比下各重复计算1 000次,结果如图7所示。图7中极限误差代表能正确解出频率为2.2 GHz的载波相位时延和带宽为147 MHz的宽带群时延的最大误差,分别为0.075 8 ns和1.133 8 ns。1 000次重复实验后统计得到,在信噪比为0 dB时,误差满足解载波相位模糊的概率为99.88%;在信噪比为-30 dB时,误差满足解载波相位模糊的概率为99.91%,验证了理论和仿真分析的正确性。
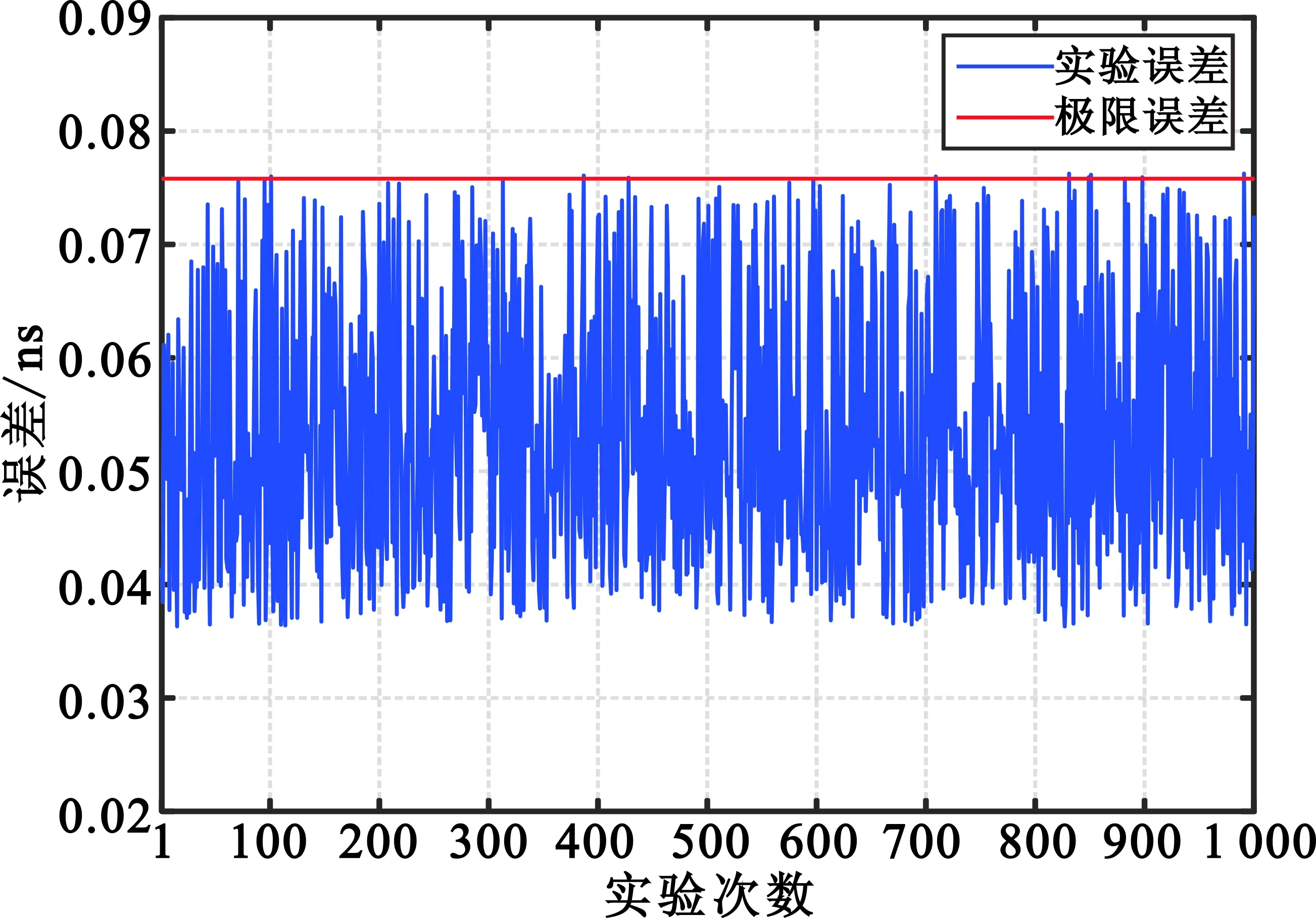
(b)信噪比为0 dB条件下时延估计误差图7 1 000次实验误差统计Fig.7 Error statistics of 1 000 experiments
5 结束语
本文分析了CEI载波相位模糊的产生条件,提出了一种利用伪码测距信号辅助解模糊的方法。明确了不同基线以及不同频段下解模糊对伪码参数选择的限制条件,设计了利用伪码测距信号辅助解模糊的实现流程。以50 km基线长度为例,仿真结果表明,信噪比较高时可以满足S频段载波相位解模糊的需求,信噪比较低时不具备直接解载波相位模糊能力但是可以解宽带群时延的相位模糊。
在深空伪码测距中,往往通过增大码长来提高无模糊距离,一般其码长都远远大于本文中所采用的8 001,在伪码速率相同的情况下,都可以满足本文设置条件。
本文提出的算法建立在具有伪码测距能力的前提下,而且对伪码速率有较高的要求,对于不具备此条件的测站需要研究其他的载波相位解模糊方法。
:
[1] EDWARDS C D.Goldstone intracomplex connected element interferometry[R]//TDA Progress Report 42-101.Washington DC:NASA,1990:1-12.
[2] 李晓杰,杜兰,黄金.基于CEI定轨中整周模糊度问题处理方法的研究[J].空间科学学报,2011,31(5):659-665.
LI Xiaojie,DU Lan,HUANG Jin.Research on ambiguity solution in CEI-based orbit determination[J].Chinese Journal of Space Science,2011,31(5):659-665.(in Chinese)
[3] 韩松涛,陈略,任天鹏,等.中国深空网首次ΔDOR联合测轨试验分析[J].飞行器测控学报,2014,33(3):258-261.
HAN Songtao,CHEN Lue,REN Tianpeng,et al.Analysis of the first multi-agency joint ΔDOR tracking of China's deep space network[J].Journal of Spacecraft TT&C Technology,2014,33(3):258-261.(in Chinese)
[4] MARTIN T,ANTREASIAN P G,BORDER J,et al.Use of very long baseline array interferometric data for spacecraft navigation [R]//ISTS 2006-d-50.Washington DC:NASA,2006:1-6.
[5] BAGRI D S.A proposed frequency synthesis approach to accurately measure the angular position of a spacecraft [R]// IPN Progress Report 42-163.Washington DC:NASA,2005:1-7.
[6] 刘庆会,史弦,菊池冬彦,等.上海和乌鲁木齐射电望远镜的超高精度同波束VLBI观测[J].中国科学G辑,2009,39(10):1410-1418.
LIU Qinghui,SHI Xian,FUYUHIKO K,et al.High-accuracy same-beam VLBI observations using Shanghai and Urumqi Telescopes[J].Science China Series G,2009,39(10):1410-1418.(in Chinese)
[7] 吴伟仁,王广利,节德刚,等.基于ΔDOR信号的高精度VLBI技术[J].中国科学:信息科学,2013,43(2):185-196.
WU Weiren,WANG Guangli,JIE Degang,et al.High-accuracy VLBI technique using ΔDOR signals[J].Scientia Sinica Informatiois,2013,43(2):185-196.(in Chinese)
[8] 路伟涛,洪家财,杨文革.基于宽带相关处理的连线干涉测量[J].装备学院学报,2014,25(2):76-81.
LU Weitao,HONG Jiacai,YANG Wenge.Connected elements interferometry based on wideband correlation processing[J].Journal of Equipment Academy,2014,25(2):76-81.(in Chinese)
[9] 任天鹏,唐歌实,刘景勇,等.基于CEI的高精度相位干涉测量试验[J].遥测遥控,2015,36(6):8-11.
REN Tianpeng,TANG Geshi,LIU Jingyong,et al.CEI-based high-precision phase interferometry tests[J].Journal of Telemetry,Tracking and Command,2015,36(6):8-11.(in Chinese)
[10] VENOSA E,ALAKIJA C,HARRIS F,et al.How to implement deep-space regenerative pseudo-noise(PN) ranging transceivers[C]//Proceedings of 2016 IEEE Aerospace Conference.Big Sky,Montana,USA:IEEE,2016:1-10.
[11] HASKINS C B,DUVEN D J,DEBOY C C,et al.First deep-space flight demonstration of Regenerative pseudo-noise ranging[C]//Proceedings of 2012 Aerospace Conference.Big Sky,Montana,USA:IEEE,2012:1-6.
[12] CONG B,MAO N,TAO X.A comparative study of ranging techniques in deep space applications[C]//Proceedings of 8th International Conference on Advanced Infocomm Technology(ICAIT 2015).Hangzhou:ICAIT,2015:1-6.
[13] 刘晓明,张鹤,吴皓威,等.高动态环境下长码扩频信号快捕算法[J].电子与信息学报,2016,38(6):1398-1404.
LIU Xiaoming,ZHANG He,WU Haowei,et al.Rapid DSSS signal acquisition algorithm under high dynamic environment[J].Journal of Electronics & Information Technology,2016,38(6):1398-1404.(in Chinese)
[14] WANG P,WANG Y Q,WU S L.A modified code tracking loop based on dual structure[J].Science China Information Sciences,2015,58(8):1-9.
[15] WANG S S,ZHU Z B,FU G.Tracking technology on phase of PN code in spread spectrum communication[C]//Proceedings of 3rd International Conference on Materials Engineering,Manufacturing Technology and Control.Taiyuan:IEEE,2016:546-549.
