一种对流层散射通信斜延迟估计方法*

，

(空军工程大学 防空反导学院，西安 710051)

1 引 言

当无线电波在对流层中传播时，除沿途遭受折射外，还被对流层散射体再次辐射，这种通信方式即对流层散射通信。对流层散射可以做超视距传播，使其在微波视距传输不可用时发挥作用。但由于对流层作用，电波在其中传输速度不等于真空中传播速度，同时传播路径也发生弯曲，产生延迟效应，因此需要估计对流层延迟[1]。

常见的对流层延迟改正模型包括天顶延迟(Zenith Troposphere Delay,ZTD)改正模型和斜延迟(Slant Propagation Delay,SPD)改正模型[2-8]。虽然这些映射函数在GPS导航定位以及卫星通信中应用广泛，所计算的对流层斜延迟也比较准确[9]，但是在对流层散射通信中直接应用存在两个问题：一是对流层散射通信中天线波束仰角一般都小于5°，映射函数方法在仰角小于5°的情况下误差成几何倍数增长；二是对流层散射通信中电波信号在对流层内散射延迟比穿透延迟要小[10]。

文献[11]在获取完整大气结构参数后以基于探空数据的射线描迹法计算的对流层延迟作为真值，分析比较了所提方法的准确性。文献[12]提出了改进的射线描迹法并采用无人机校飞外场数据，验证了“神舟”系列飞船的对流层折射修正。可见只要获取完整大气结构参数后，射线描迹法能够精确计算电波传播轨迹和对流层斜延迟。获取气象参数的是计算对流层延迟的关键，目前主要有探空气球探测和模型计算两种方法。探空气球探测存在实时性差、费时费力等缺点，除非要求特别高的场合。借鉴这一思路，本文提出一种基于射线描迹法的对流层散射通信延迟计算方法，利用全球压力和温度2(Global Pressure and Temperature 2，GPT2)模型计算射线描迹中不同分层的气象数据[13]，与文献[11-12]中的方法相比，摆脱了对探空数据的依赖。最后对北京(BJFS)、昆明(KUNM)和拉萨(LHAS)三站进行计算分析，结果表明，所提方法能够很好地进行对流层通信延迟估计，在不同仰角与时间下的结果与实际相符，为对流层散射通信计算分析提供了一种新的思路。

2 理论模型

计算对流层斜延迟需要获取测站的准确气象数据(气压P、温度T、水汽压e)[14]，为解决实时获取气象数据的难题，引入GPT2模型。GPT系列模型是Boehm 等人构建的全球气象数据模型，经历了GPT、GPT2模型的改进。GPT2包含GPT2基本模型和GPT2W模型，该系列模型使用简单方便，只需要输入测站的经纬高坐标和年积日就能输出任一点的气象数据。GPT2相对于GPT增加入了半年周期项、加权气温均值和水汽压下降速率，并同时分别估计每个格网点上平均周期、年周期和半年周期的气温递减率，整体精度提高了40%[7]，故本文选用GPT2气象模型。

2.1 GPT2模型

GPT2模型是基于欧洲(ERA)中尺度全球10年(2001～2010)月均气象参数剖面(包括气温、气压、湿度和重力势)，其输出参数是气压、温度、温度下降梯度、水汽压和VMF1映射函数的系数，并能以1°或者5°的经度和纬度分辨率提供显示[15]。每个格网点的输出参数通过120个月值产生，公式中的均值A0、年化值(A1,B1)和半年值(A2,B2)通过最小二乘法进行估计。每个参数r(t)可通过下式计算：

(1)

式中：doy是简化儒略日；A0、A1、A2、B1和B2的值保存在ASCII文件中，可在http://ggosatm.hg.tuwien.ac.at/DELAY/SOURCE/GPT2w/gpt2_1wA.grd中下载。

GPT2模型的输入参数是测试点的经度、纬度、海拔高度及简化儒略日。通过模型选择与测试点最相近的4个格网点，然后通过公式(1)计算每个格网点的输出参数。通过内插和外推计算4个格网点在测试点海拔高度的参数值，然后内插得到测试点的高度值。气压、温度和水汽压的改正可以通过下式计算得到[16]：

(2)

式中：T0和P0分别是格网点的温度和气压；T和P分别是格网点由于高度增加dh的温度和气压；dT是温度下降梯度；Q是湿度；e是水汽压；gm是重力，gm=9.806 65 m/s2；dMtr是空气的摩尔质量，dMtr=28.965×10-3kg/mol；Rg是气体常量，Rg=8.314 3 J/K/mol。

最后步骤是双线性内插格网点与测试点的输出参数。

2.2 射线描迹法

电波在地球大气中传播会产生折射现象，必须对电波折射误差进行修正。常用的方法包括地面折射率回归预报法[17]和射线描迹法[14]。由于射线描迹法是通过对大气数据分层积分计算，由于其在每个分层内能无限逼近实际折射情况，故其改正精度更高。如图1所示，Pi是大气分层离散点，Si是大气分层离散点的折射率。

图1 射线描迹法示意图Fig.1 Diagram of ray tracing

测试点天线高度为h0，假设测试点位置为地球表面A处，地球地心位置为O，电磁波上目标点为B，地心张角为φ，在测试点处的视在仰角和视在距离分别为θ0和Re，真实仰角和真实距离分别为α0和R0，其关系结构图如图2所示。

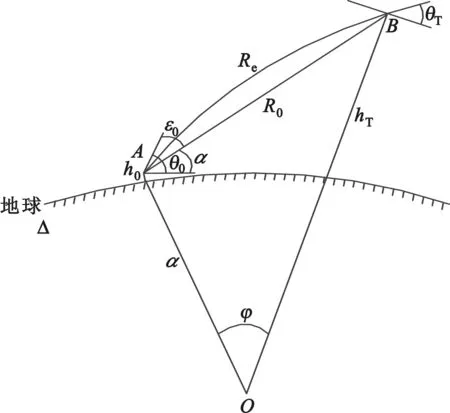
图2 电磁波传播轨迹示意图Fig.2 Diagram of electromagnetic wave propagation tracing

由于对流层折射造成的斜延迟ΔR为

(3)

式中：S为电磁波传播路径；N为大气折射率，n为大气折射指数，N=(n-1)×106；θ为电磁波传播仰角；h0为测点的海拔；hT为目标点的高度。

根据Snell定理可得

(4)

式中：h为高度的积分变量，n0为测点处的折射指数，θ为测点出的电磁波仰角，a为地球的平均半径。

由式(3)和式(4)可以计算出

(5)

地心张角为

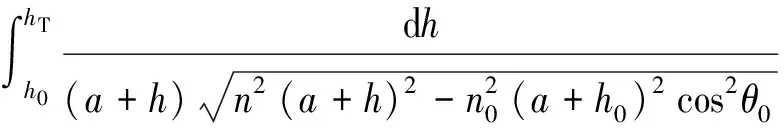
(6)

根据正弦定理可得真实仰角为

(7)

根据正弦定理可得真实距离

(8)

于是可计算

(9)

不同于卫星双向时间比对中电磁波信号穿透对流层，在对流层散射通信中电磁散射发生在对流层内，因此要计算出发生对流层散射的高度，即图3中BE的高度hT。从A点作AF⊥OB交OB于点F。

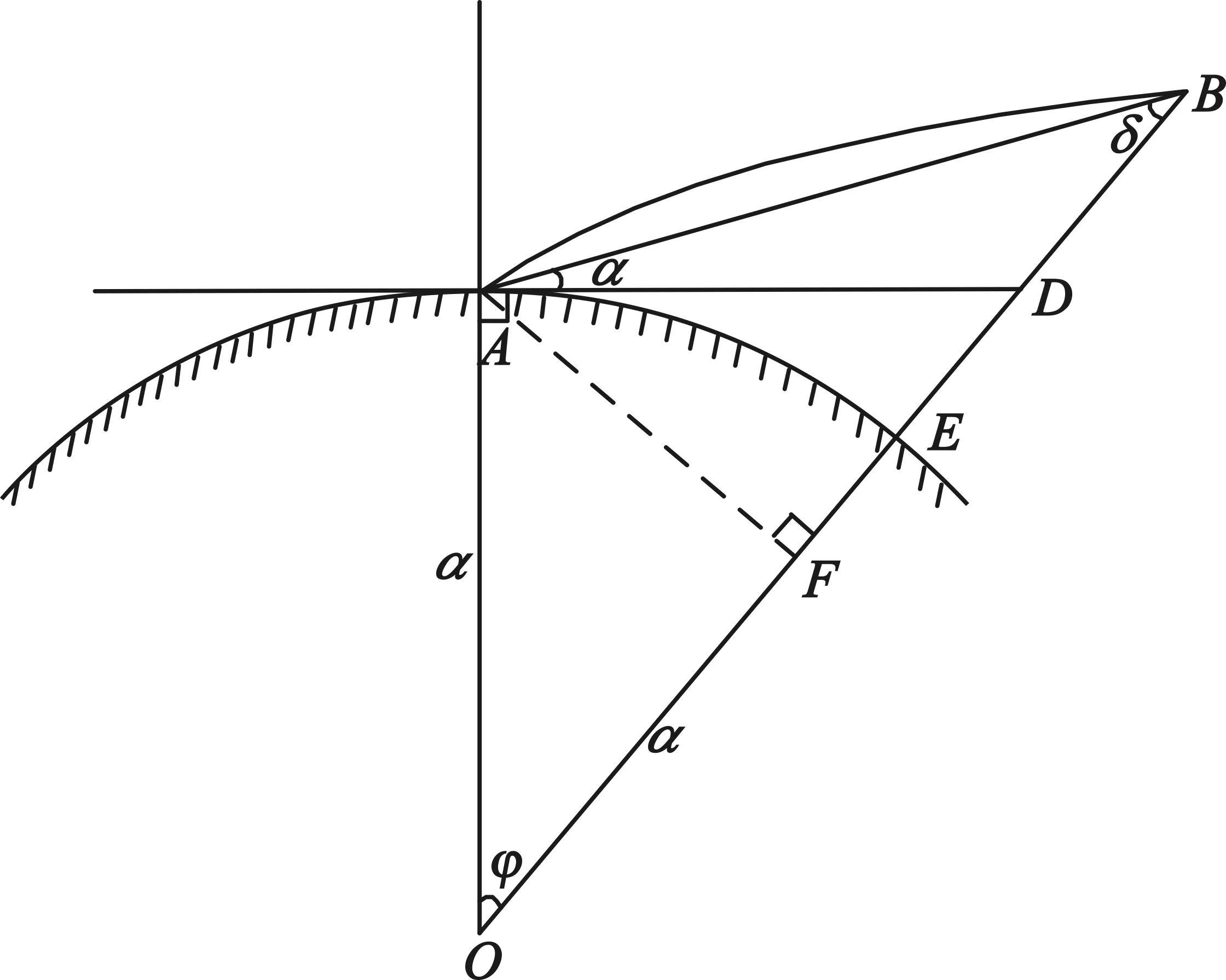
图3 射线描迹法辅助图Fig.3 Diagram of the ray trace in the atmosphere

在ΔOAB中，

α+φ+δ+π/2=π，

(10)

δ=π/2-α-φ。

(11)

在ΔOAF中，

AF=OA·sinφ=a·sinφ，

(12)

OF=OA·cosφ=a·cosφ。

(13)

在ΔAFB中，

FB=AF/tanδ=a·sinφ/tanδ，

(14)

OB=OF+FB=a·cosφ+a·sinφ/tanδ。

(15)

因此，当次对流层散射通信的大气顶层高为

hT=EB=OB-OE=a·cosφ+a·sinφ/tanδ-a=

a·cosφ+a·sinφ/tan(π/2-α-φ)-a。

(16)

式中：φ=L/R。

2.3 计算流程

Step1 输入测试点的经度、纬度、大地高和简化儒略日，系统计算与之最相近的4个格网点坐标，根据式(1)计算每个格网点气象数据。

Step2 利用公式(2)将Step 1计算的气象数据归算到测试点的高度。

Step3 对Step 2计算的4个格网点的气象数据进行双线性内插，得到测试点的气象数据。

Step4 按照高度计算每个层的气象数据，并按照Hopfield模型计算对应层的大气折射率。

Step5 根据计算的每层气象数据利用射线描迹法计算特定入射角和特定时间的对流层斜延迟。

Step6 计算多角度和时间维度下的对流层通信延迟。

3 算例与分析

3.1 站点选取与数据设置

根据对流层延迟统计信息，对流层延迟与测量站处的纬度和海拔高度密切相关，因此选取不同纬度和海拔高度的测量站进行分析比较。本文所选测量站站均位于中国境内，分别选取高纬度低海拔的BJFS站、低纬度中高海拔的KUNM站和低纬度高海拔的LHAS站进行分析比较，3个测站的具体信息见表1。

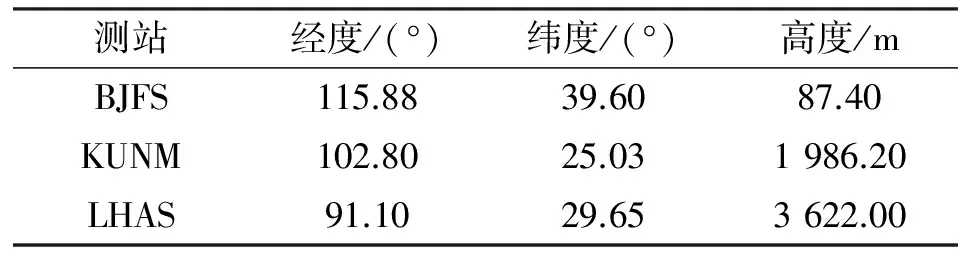
表1 所选测站信息Tab.1 Information of selected stations

为验证算法的有效性，首先计算对流层天顶延迟并进行比较分析，即将α设为0°时的对流层延迟。选取上述3个测站作为测试对象，利用所提方法，计算2012年各站的对流层天顶延迟。比对数据选为IGS提供的实测数据。将计算的对流层天顶延迟与实测值进行对比，可以得到3个测站的误差(bias)如图4所示。对每个测站的全年误差数据计算年平均误差(Mean Error,ME)和年绝对值误差(Mean Absolute Error,MAE)，结果见表2。

(a)BJFS站计算结果

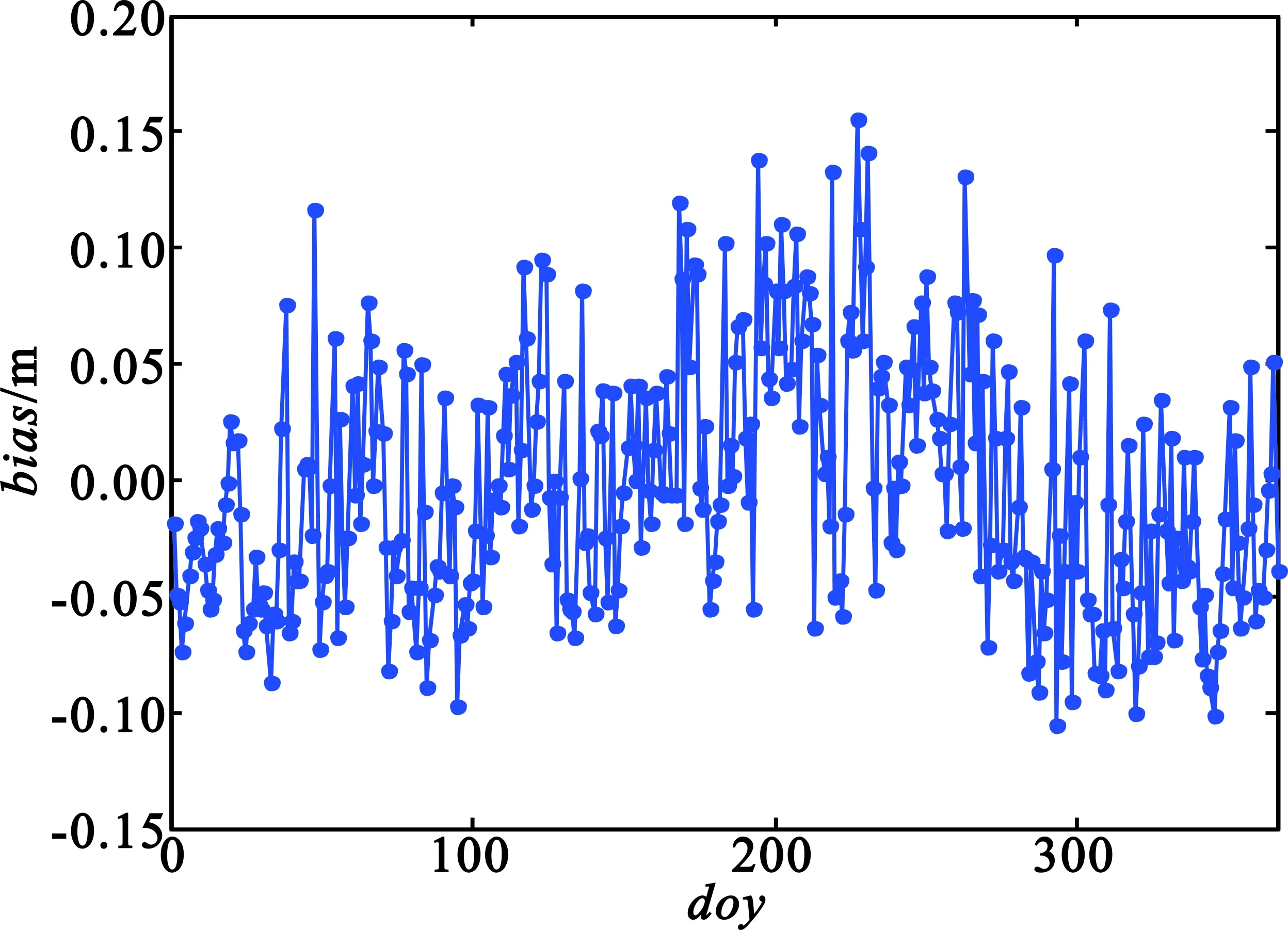
(b)KUNM站计算结果

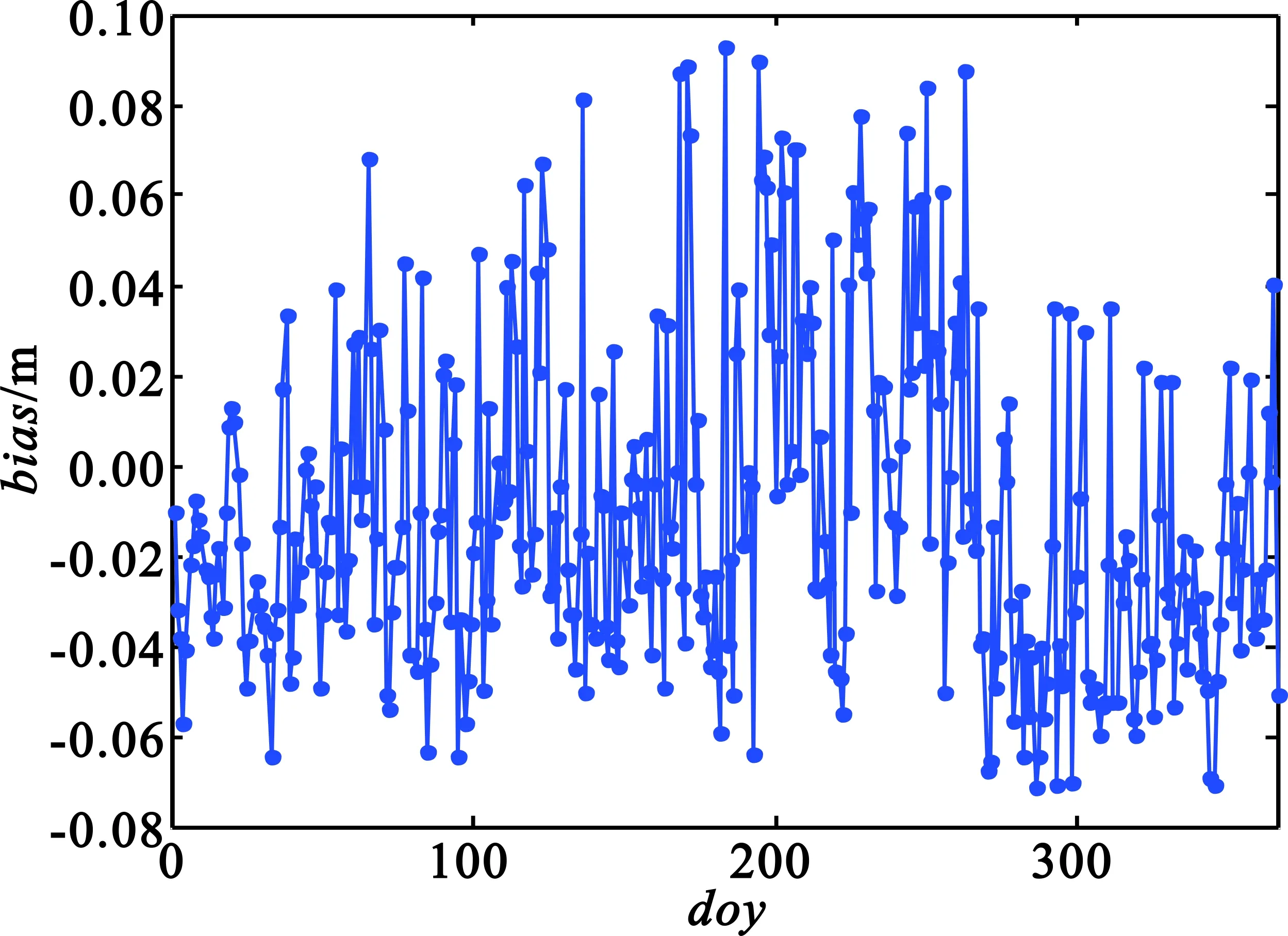
(c)LHAS站计算结果图4 各个测站天顶延迟偏差Fig.4 The bias of ZTD

表2 各个测站的计算结果Tab.2 The calculation of three stations

由图4和表2可知，3个测站的年均天顶延迟误差均在15 mm以内，考虑到计算年均天顶误差时存在正负抵消，计算其年均天顶延迟误差绝对值也在45 mm以内，能够满足精度要求。其中BJFS与KUNM站的误差值相差不大，LHAS站的误差值最小。然后进行对流层通信延迟计算分析,采用2010年1月1日至2010年12月31日1年的GPT2数据进行计算，每个仰角下时间采样周期为τ=6 h，因此每个测站每个仰角下共有1 460个数据。考虑到对流层散射通信在实际应用中天线仰角均为低仰角，一般为0°～5°，因此主要进行0°～5°仰角下的对流层通信延迟分析。每个时间下仰角的分辨率为ω=0.01°，因此每个时间下共有500个数据。每个测站一年的所有数据个数为1 460×700=730 000。

3.2 结果分析与比较

站点选择与数据分辨率设置完毕后，将纬度、高程和简化儒略日输入GPT2模型，算出气象数据后依据射线描迹法求出不同情况下的对流层通信延迟信息，结果如图5所示。

(a)BJFS站

(b)KUNM站

(c)LHAS站图5 对流层通信延迟计算结果图Fig.5 Calculation results of tropospheric delay

由图5可以看出：

(1)3个站的对流层通信延迟量均未超出12 m，按照电磁波的传输速度，可得最大时间延迟为40 ns;

(2)对比KUNM和LHAS站，两者纬度相差不大，不同的高度造成两者对流层延迟差异，且高度大的LHAS站延迟量较小，这与对流层分布特征相吻合;

(3)3个站均呈现出季节波动特性，夏季对流层延迟大，冬季对流层延迟小，这与我国夏季高温多雨，冬季寒冷干燥的气候特征相吻合;

(4)3个站均呈现出仰角越小，对流层延迟越大的特征，最大量均出现在0°仰角下。

为分别比较不同时刻和仰角下对流层通信延迟量的情况，以BJFS站为例进行分析，对上一步计算的对流层延迟量分别按照不同时刻和不同角度进行再次作图，结果如图6和图7所示。

图7 不同仰角下对流层延迟量Fig.7 Tropospheric delay at different elevation angle

通过分析图6和图7可以得出以下结论：

(1)不同时刻下对流层延迟量差别较大，从第100天(约4月中旬)开始急剧增大，最大值出现于第200天(约7月中旬)，从第320天(约10月下旬)开始降到最低水平附近;

(2)随着仰角的减小，对流层延迟量开始变大，在1°仰角附近开始急剧增大，1°仰角以上时延迟量为2 m以下，在0°仰角时达到最大值8 m。

4 结 论

本文提出了一种不依赖探空数据的对流层散射通信延迟理论计算方法，首先利用GPT2模型计算气象数据，再采用精确的射线描迹法对对流层散射通信延迟进行分层积分求和，最后选取了3个典型测站进行了算例分析，结果表明我国地区对流层散射通信延迟量最大达40 ns，且呈现出夏季大、冬季小且随着仰角减小而增大的分布特征。本文计算结果为研究我国对流层延迟分布与对流层散射通信信道特性提供了参考，为研究在不进行信道测量的情况下计算单次对流层散射通信中对流层延迟量提供了一种新思路。

：

[1] 张明高. 对流层散射传播[M].北京:电子工业出版社,2004.

[2] YAOY B,HU Y F,YU C,et al.An improved global zenith tropospheric delay model GZTD2 considering diurnal variations[J].Nonlinear Processes in Geophysics,2016,23(3):127-136.

[3] YAO Y B,ZHANG B,XU C Q,et al.A global empirical model for estimating zenith tropospheric delay[J].Science China Earth Science,2016,59(1):1-11.

[4] SILES G A,RIERA J M,GARCA-DEL-PINO P. An application of IGS zenith tropospheric delay data to propagation studies:validation of radiometric atmospheric attenuation[J].IEEE Transactions on Antennas and Propagation,2015,64(1):262-270.

[5] CHEN Q M,SONG S L,ZHU W Y. An analysis of the accuracy of zenith tropospheric zenith delay calculated from ECMWF/NCEP data over Asia[J].Chinese Journal of Geophysics,2012,55(3):275-283.

[6] SCHINDELEGGER M,PAIN G,WEBER R. Development of an improved empirical model for slant delays in the troposphere(GPT2w)[J].GPS Solutions,2015,19(3):433-441.

[7] LAGLER K,SCHINDELEGGER M,BOHM J,et al.GPT2:empirical slant delay model for radio space geodetic techniques[J].Geophysical Research Letters,2013,40(6):1069-1073.

[8] KROSZCZYNSKI K. Angular distributions of discrete mesoscale mapping functions[J].Acta Geophysica,2015,63(4):1126-1149.

[9] KALITA J Z,RZEPECKA Z,KRZAN G. Evaluation of the possibility of using the predicted tropospheric delays in real time gnss positioning[J].Artificial Satellites,2014,49(4):179-189.

[10] 朱庆林,吴振森,赵振维,等. 单台地基卫星导航接收机测量对流斜延迟[J].电波科学学报,2010,25(1):37-41.

ZHU Qinglin,WU Zhensen,ZHAO Zhenwei,et al.Tropospheric slant delay measured by singular ground-based satellite navigation receiver[J].Chinese Journal of Radio Science,2010,25(1):37-41.(in Chinese)

[11] MÖLLER G,WEBER R,BÖHM J. Improved troposphere blind models based on numerical weather data[J].Navigation,2014,61(3):203-211.

[12] 饶爱水,李清梅,胡健,等. 箭载GPS定位临近地面卫星对流延迟改正模型[J].中国惯性技术学报,2015,23(5):670-673.

RAO Aishui,LI Qinghai,HU Jian,et al.Tropospheric delay correction model of near ground satellite position using on-board GPS[J].Journal of Chinese Inertial Technology,2015,23(5):670-673.(in Chinese)

[13] SCHULER T.The TropGrid2 standard tropospheric correction model[J].GPS Solutions,2014,18(1):123-131.

[14] 陈西宏,吴文溢,刘赞. 基于改进射线描迹法的对流层斜延迟估计[J].电子与信息学报,2016(38):2468-2474.

CHEN Xihong,WU Wenyi,LIU Zan. Estimation of tropospheric slant delay based on improved ray tracing method[J].Journal of Electronics & Information Technology,2014,18(1):123-131.(in Chinese)

[15] BOEHM J,HEINKELMANN R,SCHUH H. A global model of pressure and temperature for geodetic applications[J].Journal of Geodesy,2007,81(10):679-683.

[16] WANG M,LI B. Evaluation of empirical tropospheric models using satellite-tracking tropospheric wet delays with water vapor radiometer at Tongji,China[J].Sensors,2016,16(2):186-195.

[17] 梁月吉,任超,杨秀发,等. 结合双树复小波和广义回归神经网络的钟差预报方法研究[J].测绘通报,2016(1):6-10.

LIANG Yueji,REN Chao,YANG Xiufa,et al.Prediction of satellite clock bias based on dual-tree complex wavelet transform and GRNN[J].Bulletin of Surveying and Mapping,2016(1):6-10.(in Chinese)