一种短突发航空超短波调制解调算法及实现*

(中国西南电子技术研究所，成都610036)

1 引 言

在超短波航空通信中，发射端和接收端相对运动会导致接收信号发生多普勒频率扩展，接收端地面或者附近建筑物等对接收信号的多径反射会引起信号时域展宽，这是传输信道变化引起的主要干扰。通信过程中由于异常电磁频谱发射导致的突发干扰也是影响通信质量的主要因素。对于多径反射引起的时域干扰问题，在地面接收天线高度相比通信距离小很多时，直射波与反射波近似为同时到达，时域扩展导致的码间干扰可以忽略。多普勒频移常用自动锁相环路技术来跟踪频率变化，或者采用频率估计方法完成对信号的特征提取，达到克服多普勒频移的目的。对于突发干扰，通常采用纠错编码来克服。另外，根据文献[1]，超短波频段视距通信的信道衰落变化平缓，当通信信号持续时间小于信道衰落变化时间时，信道近似为恒参信道，因此采用短帧突发通信方式可以一定程度上克服信道衰落和突发干扰的影响。

本文首先分析了超短波航空通信信道特性，定义了适合突发通信的短帧格式，提出了适合信道特性的编码调制算法，给出了工作原理和实现过程，最后分析了编码调制算法的误码率性能和试验结果。

2 超短波航空信道特性分析

飞机对地面目标的信号传播路径不仅仅是直射路径，还有多径反射。这样，地面接收的信号包含了大量的平面波，其幅度、相位以及相对飞机运动方向的到达角度都是随机的。这些波形在地面天线周围叠加和干涉，形成了一个衰落变化的场强[2]。

当发射信号为一个单位幅度的连续波时，传输系数代表了接收信号的幅度和相位。发射波可表示为

cos 2πft=Re{exp(j2πft)}=Re{h(f,t)exp(j2πft)} 。

(1)

式中：Re表示取实部；h(f,t)是复传输系数，是发射波形的时间t和频率f的函数，衰落用h(f,t)随时间t变化的幅度来表示，h(f,t)的相位随时间变化称为随机调频，h(f,t)的幅度和相位随频率变化称为信道频率选择性衰落和相位畸变。

对一个给定的发射频率f，接收信号包含了具有不同多普勒频移的许多平面波，这将在发射频率周围造成功率谱扩展。h(f,t)的功率谱可以用含有多普勒频移的接收信号的场强来表示。

假如发射一个频率为fc的单音未调制信号，除了高斯白噪声外，接收信号通常还包含以下两个分量：一是直射分量，功率为Ps，频率为fc+fD,其中fD为直射分量的多普勒频移，这个分量表示为(2Ps)1/2cos2π(fc+fD)t；二是因多径反射而产生的漫反射分量。功率为Pd，接收信号的漫反射分量包含有k个波形，可以表示为

(2)

式中：αk(t)是第k条传播路径上接收信号的衰减因子，τk(t)是第k条传播路径相对镜面分量的传播延时，fk=(v/λ)cosθk是第k条传播路径的多普勒频移，其传播路径与飞行方向的夹角为θk。漫反射分量的总的功率Pd是所有单个波的功率的和。因此，式(2)可以写成以下形式：

(3)

式中：φk为在0～2π间均匀分布的随机相位。利用三角变换，式(3)可以表示成两个正交分量：

d(t)=x(t)cos(2πfct)-y(t)sin(2πfct) 。

(4)

式中：

在一个给定的时间t，x(t)和y(t)是k个独立的零均值随机变量的和。利用中心极限理论，x和y可以近似为两个具有相等方差的零均值高斯随机变量:

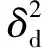
(5)

因此，可以得出结论:衰落为莱斯分布，莱斯因子Ps/Pd可变，它依赖于飞机的高度和地面反射系数。

在实际应用中，多数用在开阔地带的空地数据传输，通信距离较远，反射波与直射波到达时间差可以忽略，因此多径影响可以不考虑,而在此信道中，多普勒频移和突发脉冲干扰是通信质量恶化的主要原因。多普勒频移通过对前导载波信号的捕获和跟踪达到同步进行克服。传统的纠错编码，如BCH码、卷积码，纠突发错误的效果并不好。在分组码中，有一类非二进制BCH码——RS码，它由码符号组成，纠错以符号为单位进行，这样一次可纠多个突发错误，因此RS码非常适合纠突发错误[3]。而在各种调制技术中，相位调制更适合于莱斯衰落信道[4]。因此，多相调制和RS码相结合[5]，将可以获得较好的误码性能。

3 算法设计与实现

3.1 帧格式设计

信号帧格式的定义与采用的调制解调技术是息息相关的，因此有必要对采用的信号格式进行说明。本文采用的信号帧格式中，每个短帧为一个处理周期。其中：载波前导序列为连续整周期的未调制载波信号；载波前导序列后，紧跟着的是帧同步序列，帧同步序列提供数据帧的起始位置，建立码元同步，同时为后续的数据解调提供相位基准；帧同步序列后就是数据帧序列，包含信息码和纠错检验码。

3.2 载波同步

在同步传输信息的调制系统中，当采用同步接收或相干检测时，接收端需提供一个与发射端调制载波同频同相的本地载波，即接收端需要实现与发端信号的载波同步，包括载波频率、幅度和相位的同步。在本系统中，需要从一个记录不完全且较短时间的前导同步序列中估计出载波信号的频谱。解决这种问题的技术可以归结为两类：一类是基于某种形式的参数估计，比如基于反馈闭环的频谱估算算法[6]，有很高的分辨率和适应性,但是需要长时间的持续跟踪和闭环计算，不适合短突发通信方式；一类谱估计算法是基于傅里叶变换(Fast Fourier Transform,FFT)的[7],这种算法有容易实现和速度相对较快的优点，但需要克服估计结果不很精确的缺点，同时本身还有周期性的假设，会因为数据的周期性和FFT的周期性不匹配，因边缘效应而恶化。文献[8]提出的数字FFT结合频域插值的方法克服了基于FFT频谱估计的缺点，同时其快速计算特性可以实现对短突发载波前导序列的快速精确估计，达到载波同步。

通过对未调制载波的N个采样数据进行快速傅里叶变换，可以得到其频域值S(K),K为数字频率，K=0,1,…,N-1。使模值|S(K)|最大的K记为Kmax，其最大模值为|S(Kmax)|，信号实际数字频率f位于Kmax±1/2范围内。

(6)

初始相位

φ(f,Kmax)=arg[S(Kmax)]+π(f-Kmax),

(7)

信号幅度

(8)

通过得到的频率、初始相位和幅度生成本地载波，就可以实现载波同步。

3.3 位同步

由于采用突发信息格式，而对于突发信息结构(相对于周期重发信号格式)的同步传输的系统中，采用了同步帧头只发一次的帧同步结构，要求构造的帧同步码具有以下特性[9-10]：

(1)非循环自相关函数值达到最小，即在帧同步运算覆盖区内(见图1)，有很强的抗伪同步性能;

(2)具有最佳的相位识别能力，即具有尖锐的自相关函数特性，能快速准确识别;

(3)从传输效率考虑，码长应尽可能短，但是应具有较强的抗传输差错能力。

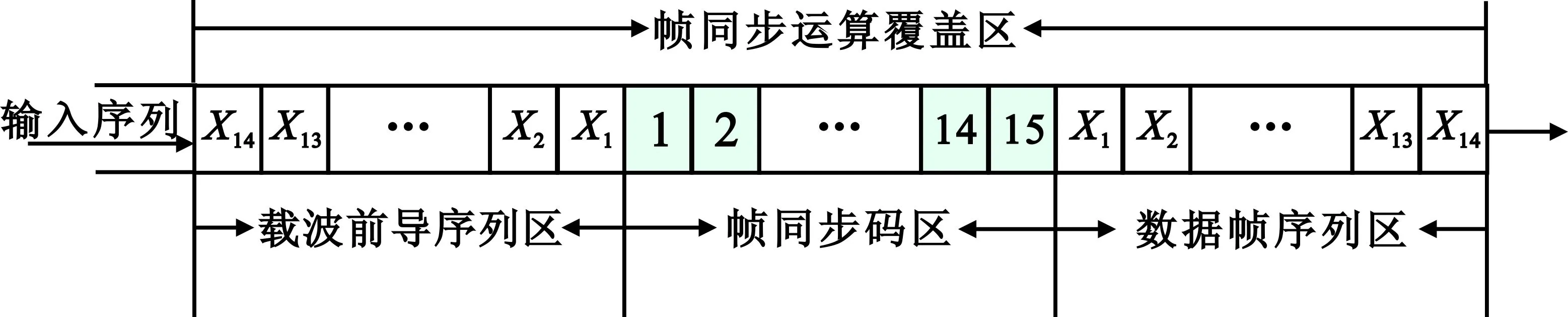
图1 帧同步过程中码的分布图Fig.1 Code distribution of the frame synchronization process

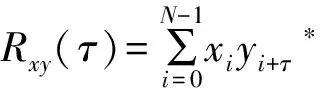
这里采用一种以伪同步概率最低为准则的最佳同步码,其定义如下：在给定的误码率及帧同步码识别器所允许的错误数目(即检测门限)条件下，用计算机搜索计算出长度为l的各种码型在覆盖区内出现的假同步概率，其中假同步概率最小的那一种码型，就是长度为l的最佳同步码。本文采用码长为15的同步码。

帧同步过程是对采样信号与本地已知信号的共轭相关的过程,如下式所示：

(9)

式中：Y*是相关码元的共轭序列，X是输入信号序列，随着新的采样数据的加入，相关窗随之移动，进行滑动相关运算。其相关过程示意图见图2。

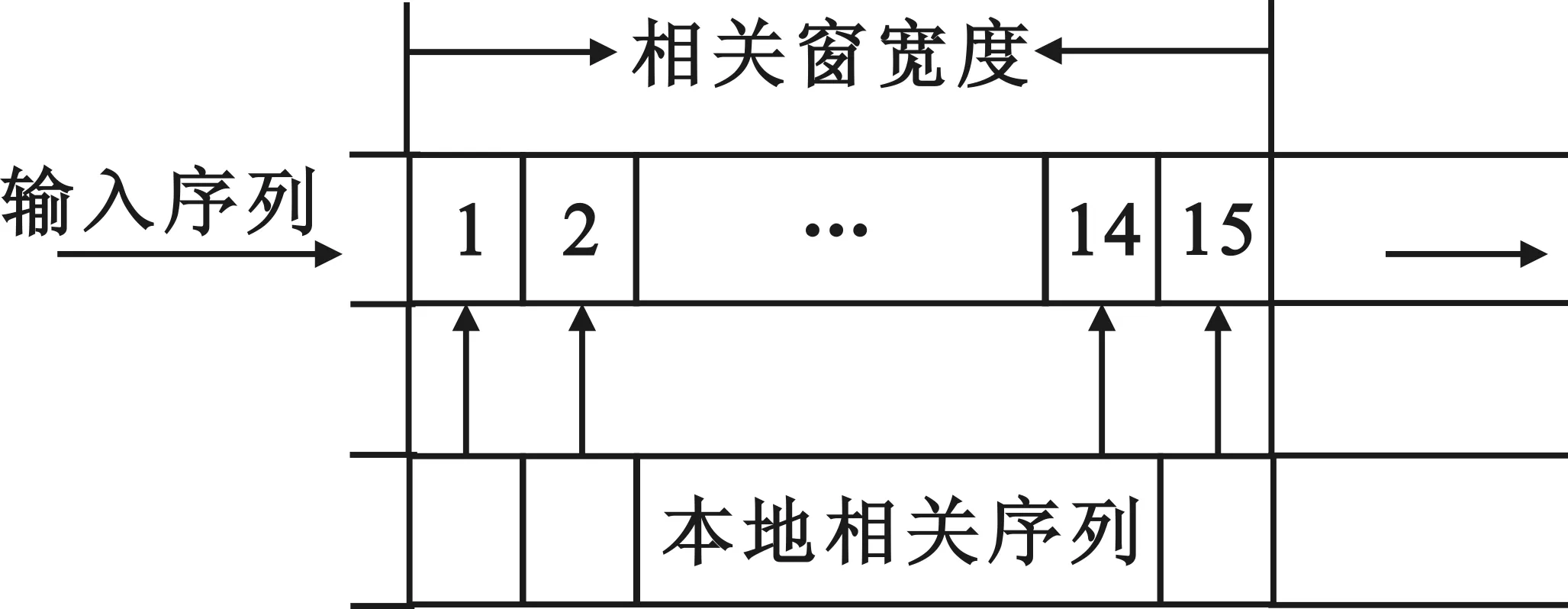
图2 帧同步相关示意图Fig.2 Diagram of the frame synchronization correlation

在帧同步捕获过程中，进行滑动相关，每新增一个采样点做一次相关运算，当相关峰超过预定的值，则认为有信号出现，其中最大的峰值所对应的样点就是最佳同步点，下一个采样点就是信息数据的起始位置。

3.4 编码调制

二进制数据流进入差分编码器，分成3个独立的二进制比特流。D8PSK差分编码器实现框图见图3，其中，T表示一个码元间隔。

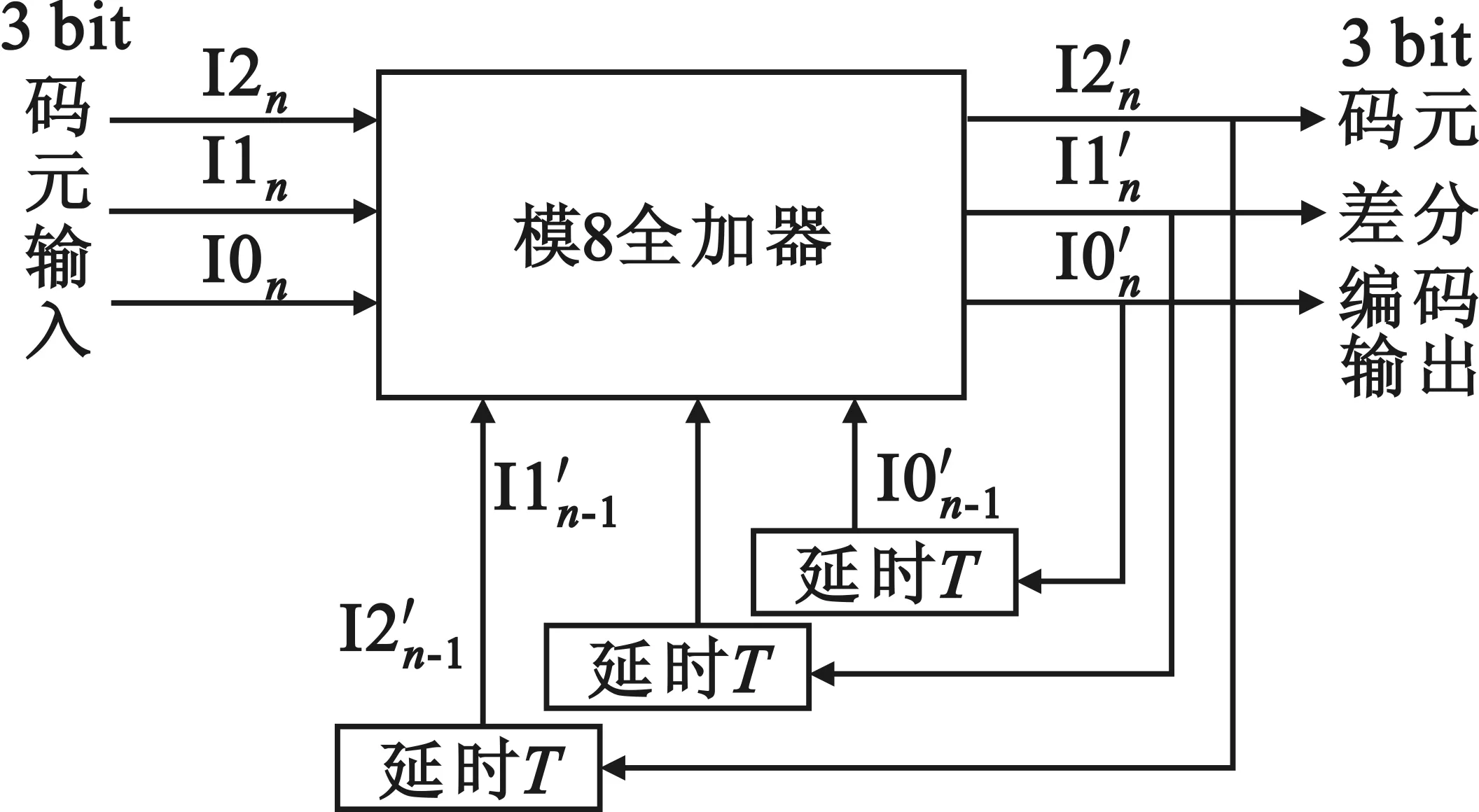
图3 D8PSK差分编码器Fig.3 The differential encoder of D8PSK

其差分编码关系如式(10)所示：

(I2′I1′I0′)=(I2I1I0) /(1-D)模8 。

(10)

式中：( )表示一个8进制码元序列，1-D表示一阶二进制多项式。

D8PSK差分解码器见图4,其差分译码关系如式(11)所示：

(I2I1I0)=((1-D)(I2′I1′I0′))模8 。

(11)

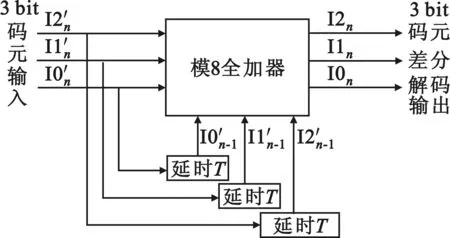
图4 D8PSK差分解码器Fig.4 The differential decoder of D8PSK

二进制数据流进入差分编码器，转换成差分码，经过差分编码以后，进行8PSK调相。当前符号的绝对相位等于φk，为了保证因为相邻相位错误导致的符号错误只有一个比特，通常要对符号进行Gray编码。发射的信号就是R(ej(2πft+φ(t))),R表示升余弦滤波。

对于矩形包络的8PSK调制信号，可以表示如下[11]：

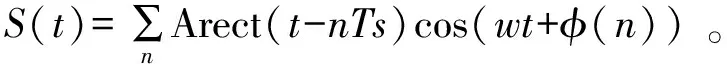
(12)

式中：A为矩形包络单位周期内的能量，φ(n)={2πi/8},i=0,1,…,7,假设初相位为零。

展开式(12)可以得到

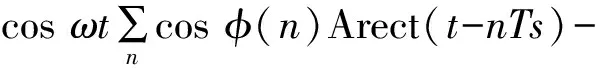
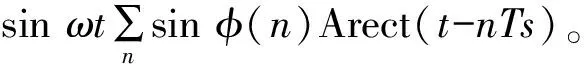
(13)

因此，从式(13)可以看出，D8PSK调制信号可以看成是两个正交载波进行多电平双边带调制后的两路MASK信号的叠加。这样，可以将式(13)写成

S(t)=I(t)cosωt-Q(t)sinωt。

(14)

其中：

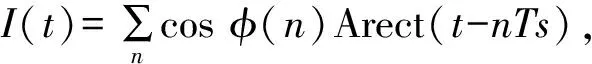
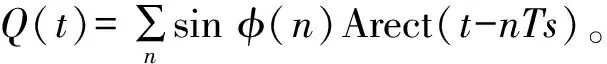
D8PSK数字调制的功能框图如图5所示，其解调过程见图6，经过正交解调后，再进行差分译码。

图5 D8PSK调制功能框图Fig.5 Diagram of the D8PSK modulation

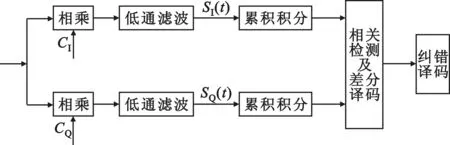
图6 D8PSK解调功能框图Fig.6 Diagram of the D8PSK demodulation

如图6所示，利用两个正交载波cI和cQ进行解调：

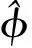
经过相乘、低通滤波后，得到解调后同相分量sI(t)和正交分量sQ(t)：

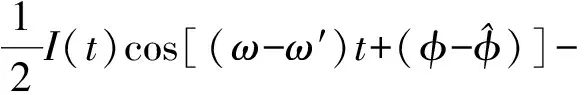
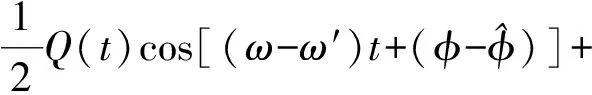
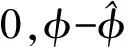
(15)

(16)

从式(15)和式(16)可以得到两路正交的相位信息，根据编码相位图就可解出8进制差分码元信息，再经过差分译码，就得到了需要的绝对码元，然后送到译码器进行纠错译码。

4 性能分析及试验结果

输入信号经过D8PSK解调后进行RS译码，其示意图见图7。

图7 D8PSK解调与RS译码
Fig.7 Diagram of the D8PSK demodulation and RS decoding

根据短帧格式设计，RS纠错码选用GF(28)RS(72，62)码，可以纠至多5个8 bit码元的随机错误，其帧错误概率如式(17)所示：

(17)

其8 bit码元错误概率

Psym=1-(1-pb)8。

式中：pb表示比特错误概率。

因此可以得到帧错误概率Pfe与输入比特错误概率pb的关系如式(18)所示:

(18)

理论分析表明，GF(28)RS(72，62)码在输入误比特率(Bit Error Rate,BER)Pb为10-3时，可以达到10-5的误帧率，见图8。

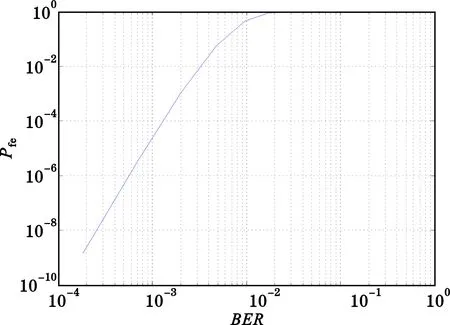
图8 GF(28) 上的RS(72，62)码的帧纠错性能Fig.8 The frame error correction performance of the RS(72,62) in GF(28)

根据D8PSK相干解调的理论分析结论，其在高斯白噪声下的误符号概率可近似表示为[12-13]

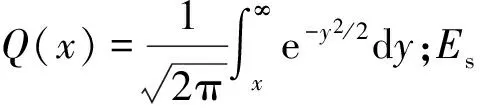
解调时，其最可能的相位判决错误出现在相位相邻区域，由于进行了Gray编码，保证因此导致的bit错误只有一位。此时，其误符号概率和误比特概率有以下近似关系：

pb≈Ps/lbM。

(19)

式中：pb表示误比特概率，M=8。

将式(19)代入式(18)可以得出帧错误概率Pfe与输入信号Es/n0的关系如下：

(20)

其中：

每个符号包括3 bit数据，因此Eb/n0与Es/n0相比差4.7 dB左右，可以容易得到帧错误概率Pfe与输入信号Eb/n0的关系曲线，其理论分析和试验数据曲线见图9。从数据曲线可以看出，本文RS-D8PSK编码调制系统在输入Eb/n0为13～14 dB(Es/n0为17～19 dB)时，其误码性能可以达到10-5，因此在实际设计中一般要求输入Eb/n0不低于14 dB。

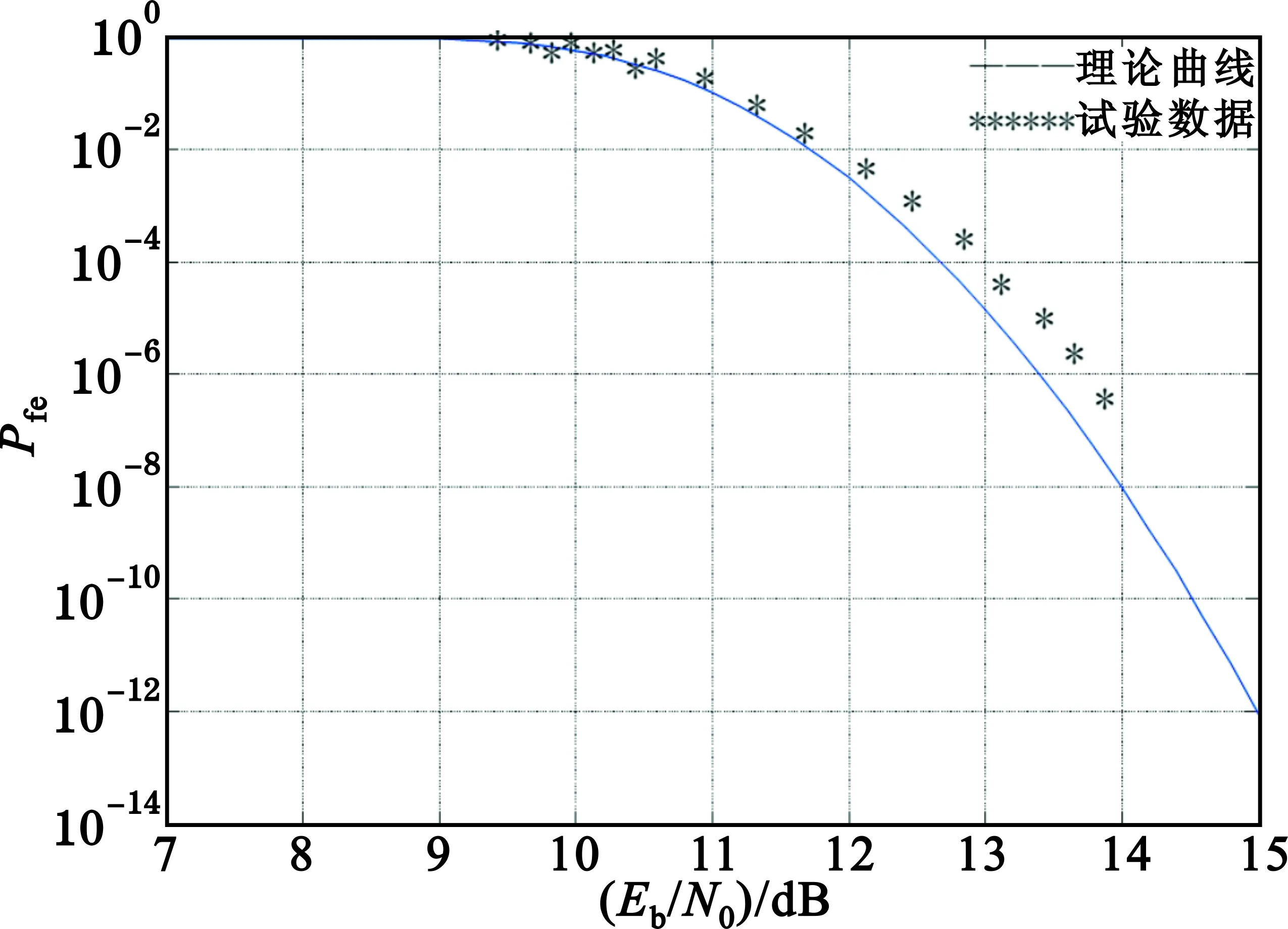
图9 D8PSK调制和RS码相结合的误码性能曲线Fig.9 The frame error rate of the D8PSK modulation plus RS(72,62) coding

5 结 论

本文针对实际工程对超短波航空通信的实际需求，提出并实现了一种适合超短波航空通信的调制解调器；根据超短波航空通信信道的特点，采用短突发的通信方式，通过快速傅里叶变换和数字相关完成载波的快速提取和帧同步。由于短帧突发、每帧同步，该调制解调算法有效地克服了信道衰落和多普勒时变。通过多相调制与RS码相结合，实现了数据的调制解调和纠错编译码，较好地适应了超短波航空信道的衰落特性和突发干扰。本文提出的调制解调算法已在飞机通信系统中采用数字信号处理器实现，试验和工程应用表明，本文实现的调制解调器与理论性能基本一致，很好地满足了超短波航空信道的应用需求。

：

[1] 曹博,刘文评,沈笑云.航空无线信道建模与仿真[J].电光与控制,2015,22(5):93-96.

CAO Bo,LIU Wenping,SHEN Xiaoyun.Modeling and simulation of aviation wireless channel[J].Electronics Optics & Control,2015,22(5):93-96.(in Chinese)

[2] ELNOUBI S.A simplified stochastic model for the aeronautical mobile radio channel[C]//Proceedings of 1992 IEEE Vehicular Technology Conference.Denver，Colorado:IEEE,1992:960-963.

[3] 王新梅，肖国镇.纠错码-原理与方法[M].西安：西安电子科技大学出版社，2001.

[4] XIONG F Q.Digital modulation techniques[M].London:Artech House Telecommunications Library，2017.

[5] WILSON S G.Digital modulation and coding[M].Englewod Cliffs,New Jersey：Prentice Hall,Inc，1988.

[6] 姜波，王世练，温东.高速率8PSK信号的载波同步及实现[J].电路与系统学报,2009,14(4)：21-26.

JIANG Bo,WANG Shilian,WEN Dong.Carrier synchronization for high rate 8PSK signals and implementation[J].Journal of Circuits and Systems,2009,14(4)：21-26.(in Chinese)

[7] 王华奎.数字信号处理及应用[M].北京：高等教育出版社，2009.

[8] 贾平生.一种适用于多相相干解调的载波同步方法[J].电讯技术，2001，41(5):70-73.

JIA Pingsheng.A carrier-synchronization method applied to poly-phase coherent demodulation communication[J].Telecommunication Engineering，2001,41(5):70-73.(in Chinese)

[9] 杨义先.最佳信号理论与设计[M].北京：人民邮电出版社,1996.

[10] 张贤达，保铮.通信信号处理[M].北京：国防工业出版社，2000.

[11] 林静，曹力，夏大旺，等.民航地空数据链中D8PSK信号解调算法[J].信息技术，2015(1):34-38.

LIN Jing,CAO Li,XIA Dawang,et al.Research on the demodulation algorithm of D8PSK based on VDL M2[J].Information Technology,2015(1):34-38.(in Chinese)

[12] 柳雨晨，张晓磊，王拥军，等.D8PSK调制格式研究及其传输性能分析[J].红外与激光工程，2012,41(5):1271-1276.

LIU Yuchen,ZHANG Xiaolei,WANG Yongjun,et al.Research on D8PSK modulation formats and analysis of its transmission performance[J].Infrared and Laser Engineering,2012,41(5):1271-1276.(in Chinese)

[13] 曹志刚，钱亚生.现代通信原理[M].北京：清华大学出版社，2012.