利用改进PAST算法的直扩信号PN码盲估计*

盛世强**a,杨文革b,陈晓威

(航天工程大学a.研究生管理大队；b.光电装备系；c.研究生管理大队,北京101416)

1 引 言

直接序列扩频(Direct Sequence Spread Spectrum，DS-SS)技术因其良好的隐蔽性、抗干扰能力和码分多址特性而被广泛地应用于卫星导航系统、航天测控、JTIDS等军事和民用通信领域中。在通信对抗领域中，DS-SS信号的盲处理研究成为热点问题，其中最关键的是伪随机(Pseudo Noise,PN)码的盲估计问题[1]。

PN码盲估计方法目前主要包括基于特征分析估计方法[2]、基于特征多项式估计方法[3-4]和基于相关运算估计方法[5-6]。与其他两种方法相比，基于特征分析估计方法估计精度高，且不受PN码类型限制，是主要的PN码盲估计方法。

根据主特征向量提取方式的不同，基于特征分析估计方法可以分为矩阵分解法、PAST方法[7-8]和神经网络法[9-10]。矩阵分解法估计精度最高，但需要对数据进行批处理，计算复杂度高，且跟踪环境变化的能力不强，难以满足实时性处理的需要。针对该问题，神经网络法和投影逼近子空间(Projection Approximation Subspace Tracking,PAST)方法在牺牲一定精度前提下均可以实现主特征向量快速提取，且PAST方法几乎不受初值设定、训练样本等因素影响，稳定性更好且估计精度更高。但PAST方法存在以下两个问题：一是固定遗忘因子无法兼顾收敛速度和精度，且不能跟踪信噪比变化，从而影响估计精度；二是在迭代进行时，依赖人工判读而不能实现迭代是否收敛的自动判断，限制了其在实际中的应用。

针对上述问题，本文提出了一种基于改进PAST算法的DS-SS信号PN码盲估计方法。在传统PAST算法的基础上，利用遗忘因子与收敛速度和收敛精度的相关性，构造了一种基于跟踪误差的自适应遗忘因子，实现了收敛速度和收敛精度的同时优化；基于收敛精度和估计精度的统计特性，确定了预期最低误码率下的迭代收敛门限，从而自动判读是否收敛，及时停止迭代运算，有效降低了计算量，提高了算法的实际应用能力。

2 DS-SS信号模型

DS-SS信号是用待传输的信息码与高速率的PN码波形相乘来实现频谱扩展。为简化分析，本文假设背景噪声为理想高斯白噪声，则接收机输出的DS-SS信号为[11]

y(t)=s(t)+n(t) 。

(1)

式中：n(t)为零均值的高斯白噪声；s(t)为DS-SS基带信号，可以表示为

(2)

式中：{c(i)=±1,i=0,1,…,P-1}表示PN码，P为PN码长度；Tc表示码片宽度；T0=PTc表示PN码周期；A表示信号幅度；t0表示失步时间；p(t)表示发射机滤波器与信道响应、接收机滤波器的卷积，在理想信道中，p(t)为矩形函数(支撑区域为[0,Tc))；{dk=±1,k∈}表示信息码，是均值为0的均匀分布。

3 基于PAST算法的PN码盲估计

基于PAST算法的DS-SS信号PN码盲估计方法以信号的特征分析为理论基础，其本质上是随机信号条件下的高斯极大似然估计，即信息码元序列假定服从高斯分布条件下的极大似然估计[12]。

3.1 DS-SS信号特征结构分析

基于上述信号模型，假设按PN码码片速率采样，且失步时间t0≠0，DS-SS信号可以表示为数据向量x(k)：

x(k)=s(k)+n(k),
s(k)=dkc1+dk+1c2。

(3)

A=[x(1),x(2),…,x(M)] 。

(4)

得到相关矩阵R:

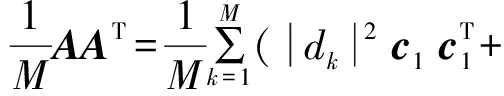
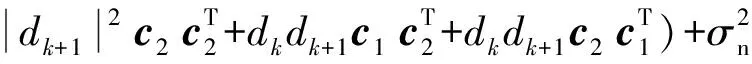
(5)

上式推导中，假设有用信号s(k)和噪声n(k)相互独立，信息码{dk|k=1,2,…}均值为0且不相关。

当M→时，得到

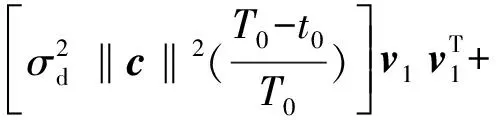
(6)

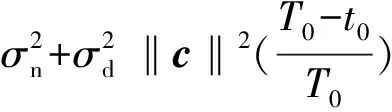
c=c1+c2=sgn(v1)+sgn(v2) 。

(7)

3.2 投影逼近子空间跟踪(PAST)算法

矩阵的特征值分解或奇异值分解需要对批量数据进行处理，跟踪环境变化的能力不强，难以满足实时性处理的需要。由德国学者 Yang Bin[13]提出的PAST算法能够通过迭代逼近的方式实现特征向量的快速提取，跟踪特征向量的实时变化。

在实际应用中，相关矩阵R可能随时间变化，从而特征值和特征向量也随时间变化。因此，基于递推最小二乘(Recursive Least Square,RLS)和自适应滤波理论的PAST算法被提出，其中，为获得更快收敛速度，在目标函数中加入遗忘因子β(0<β≤1)。文献[14]已有关于PAST算法的基本理论和具体推导过程，此处不再赘述。

在DS-SS信号PN码盲估计的研究中时，假设接收信号x已实现同步，则仅需跟踪到协方差矩阵的最大特征向量ω，则PAST算法具体步骤如下：

初始化d(0)和ω(0)，对t=1,2,…，计算

x1(t)=x(t),
y(t)=ωH(t-1)x1(t),
d(t)=βd(t-1)+|y(t)|2,
e(t)=x1(t)-ωH(t-1)y(t),
ω(t)=ω(t-1)+e(t)[y*(t)/d(t)] 。

4 PAST算法应用改进分析

3.2节从理论角度对于PAST算法在DS-SS信号PN码盲估计中的应用进行了可行性分析，但在实际应用中，还需要针对以下两个方面进行深入探讨和研究：

(1)遗忘因子β的大小影响迭代收敛的速度和精度，在实际应用时如何确定β的取值，从而在保证收敛精度的前提下尽可能加快收敛速度；

(2)在迭代过程中，如何自动判读是否收敛，及时停止迭代运算，即确定合适的迭代停止门限，从而有效降低计算量，并提高算法的实际应用能力。

本节将主要基于以上问题进行理论分析，对PAST算法作适应性改进。

4.1 收敛速度和收敛精度

遗忘因子β的大小影响迭代收敛的速度和精度。收敛速度由从开始到确定收敛所需要迭代运算的次数表示，收敛精度由收敛后相邻两次迭代运算结果之差表示，即Δω(t)=ω(t-1)-ω(t)。理论上，当迭代收敛时，Δω→0，但是Δω为一向量，不便于量化表示，根据Δω→0⟺‖Δω‖2→0，以‖Δω‖2衡量迭代是否收敛。实际中，因为无法严格满足正交性约束条件，所以‖Δω‖2最终收敛到取值区间[E‖Δω‖2±δ]，其中E‖Δω‖2为迭代收敛后‖Δω‖2的统计均值，δ为振荡半径，收敛精度越高，E‖Δω‖2越趋近于0值，波动程度越小，即δ越小。

基于3.1节分析，在采样样本无限长的理想化条件下，相关矩阵的主特征向量是原PN码归一化处理后的结果。因此，定义

R(t)=[ω(t-1)Hω(t)]1/2。

(8)

当迭代收敛时，R→1。但在实际中，随迭代进行，R呈现出与‖Δω‖2相似的曲线特性，围绕收敛统计均值ER>1上下波动，方差随ER减小而减小。

(9)

(10)

(11)

得到

(12)

(13)

(14)

(15)

所以，在迭代过程中，‖Δω‖2的变化是ω中所有变量数值变化累积的结果；对于变量R，因为ε极性随机变化，所以R的变化是所有变量数值变化极性中和后的结果，且

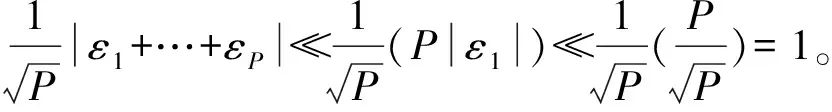
(16)

基于上述分析，迭代收敛后，R的走势比‖Δω‖2平缓，更适合作为衡量算法收敛精度的参数。

图1和图2分别是同一次迭代过程中‖Δω‖2和R的变化趋势，可以看出，在迭代大约相同次数以后(即图中标红区域)，R和‖Δω‖2均开始收敛，但相比之下，R的收敛曲线走向更加明确，收敛后变化更加平稳，方差更小。

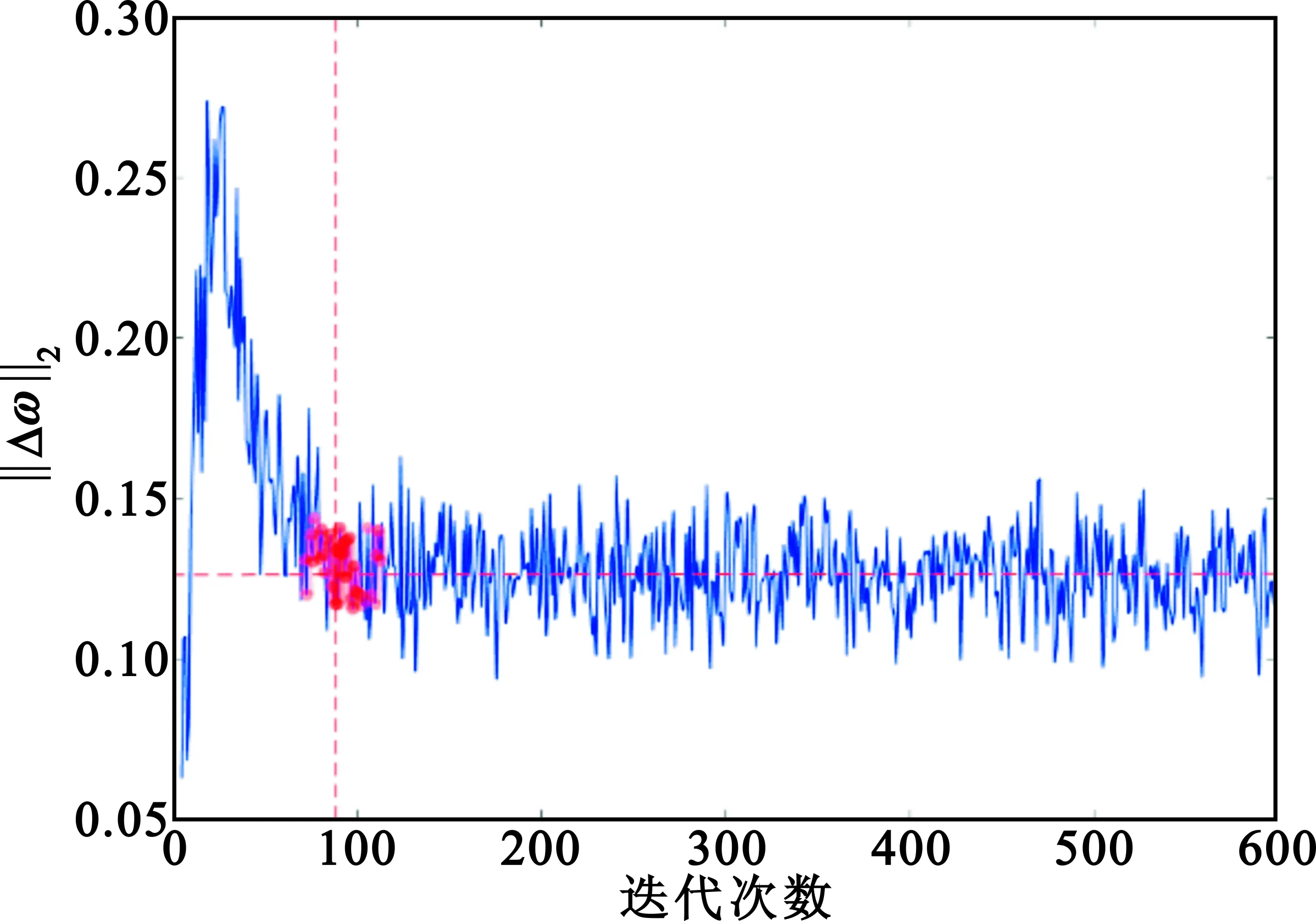
图1 ‖Δω‖2随迭代变化趋势Fig.1 ‖Δω‖2 changing with different iterations

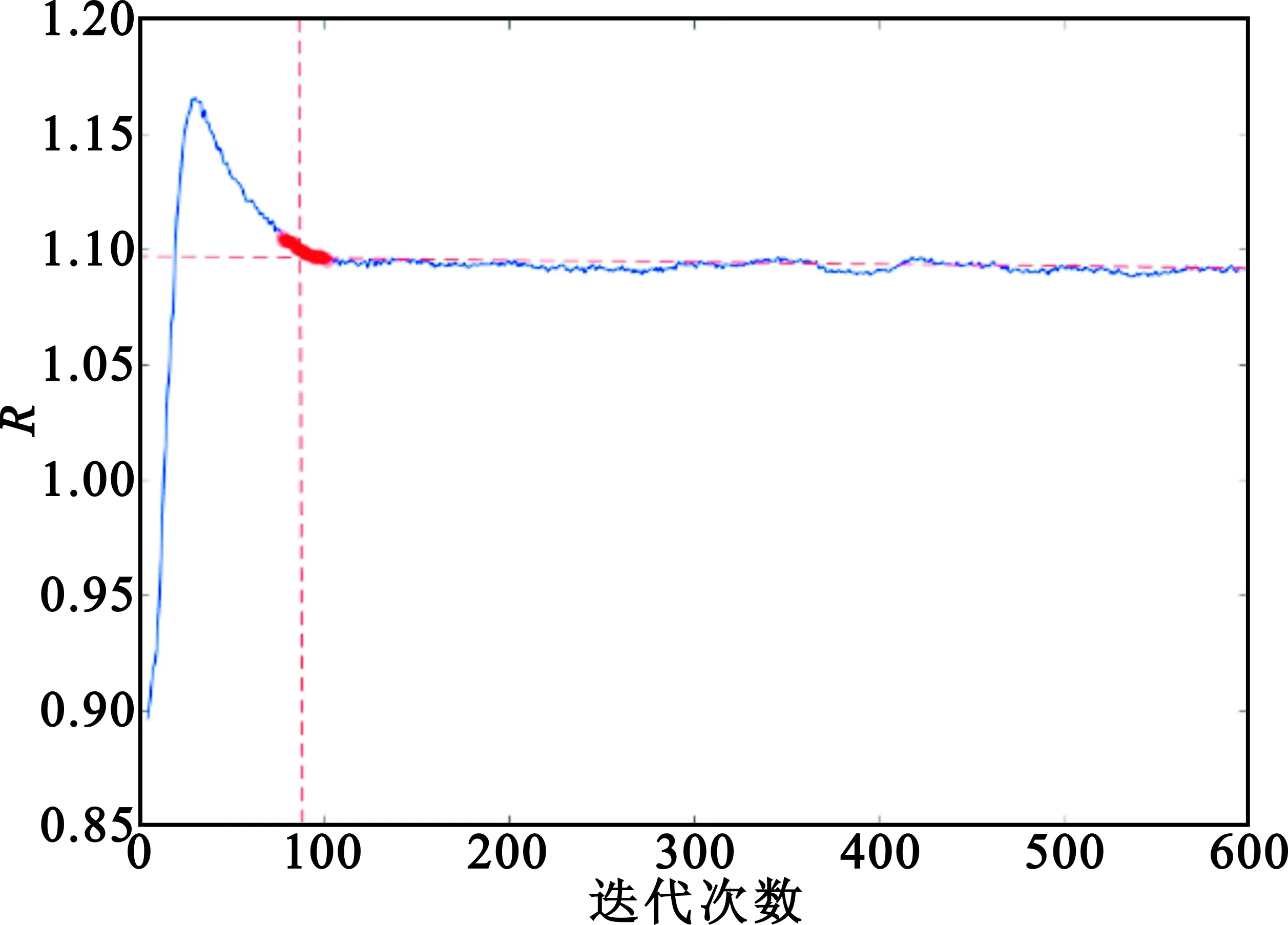
图2 R随迭代变化趋势Fig.2 R changing with different iterations

收敛精度和估计精度呈正相关，收敛精度越高，估计精度越高。估计精度通常由估计PN码的误码率(Bit Error Rate,BER)来衡量。

图3是误码率随迭代运算的变化趋势，对比图1和图2，可以看到，‖Δω‖2和R开始收敛后，误码率变化也趋于稳定，围绕某一定值作小范围波动，而不再呈明显下降趋势。因此，从估计精度的角度出发，选择R作为衡量迭代是否收敛的参数是正确的。

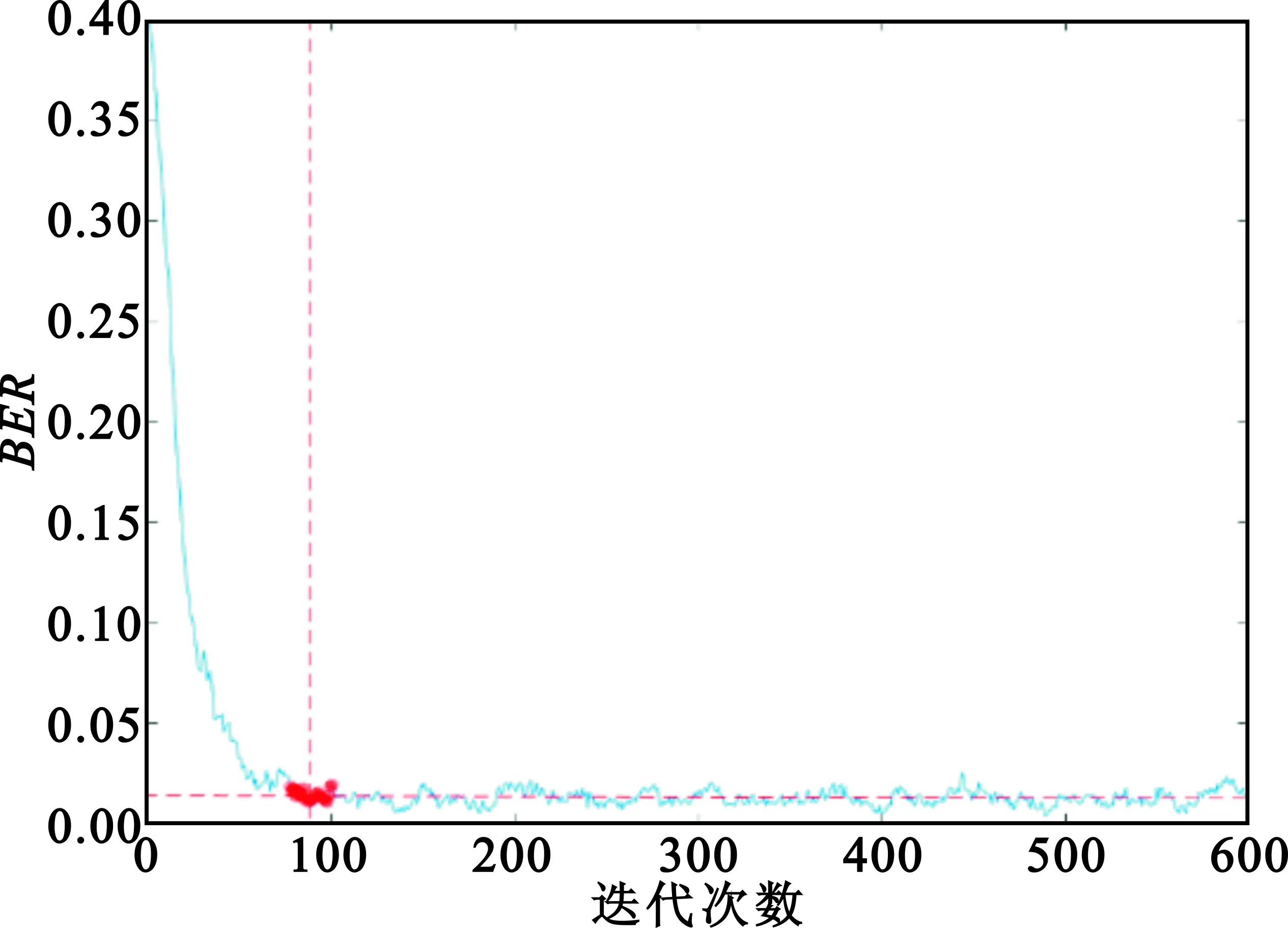
图3 BER随迭代变化趋势Fig.3 BER changing with different iterations

4.2 自适应遗忘因子

遗忘因子β是PAST算法迭代开始前人为设定的关键参数，β越小，收敛速度越快，但收敛精度越差；反之，β越大，收敛精度越高，但收敛速度越慢。图4是在相同的初始向量、接收信号和信噪比环境下，基于不同的遗忘因子(β分别等于0.8、0.9、0.95、0.99)R随迭代进行的变化趋势，标红区域表示迭代开始收敛。

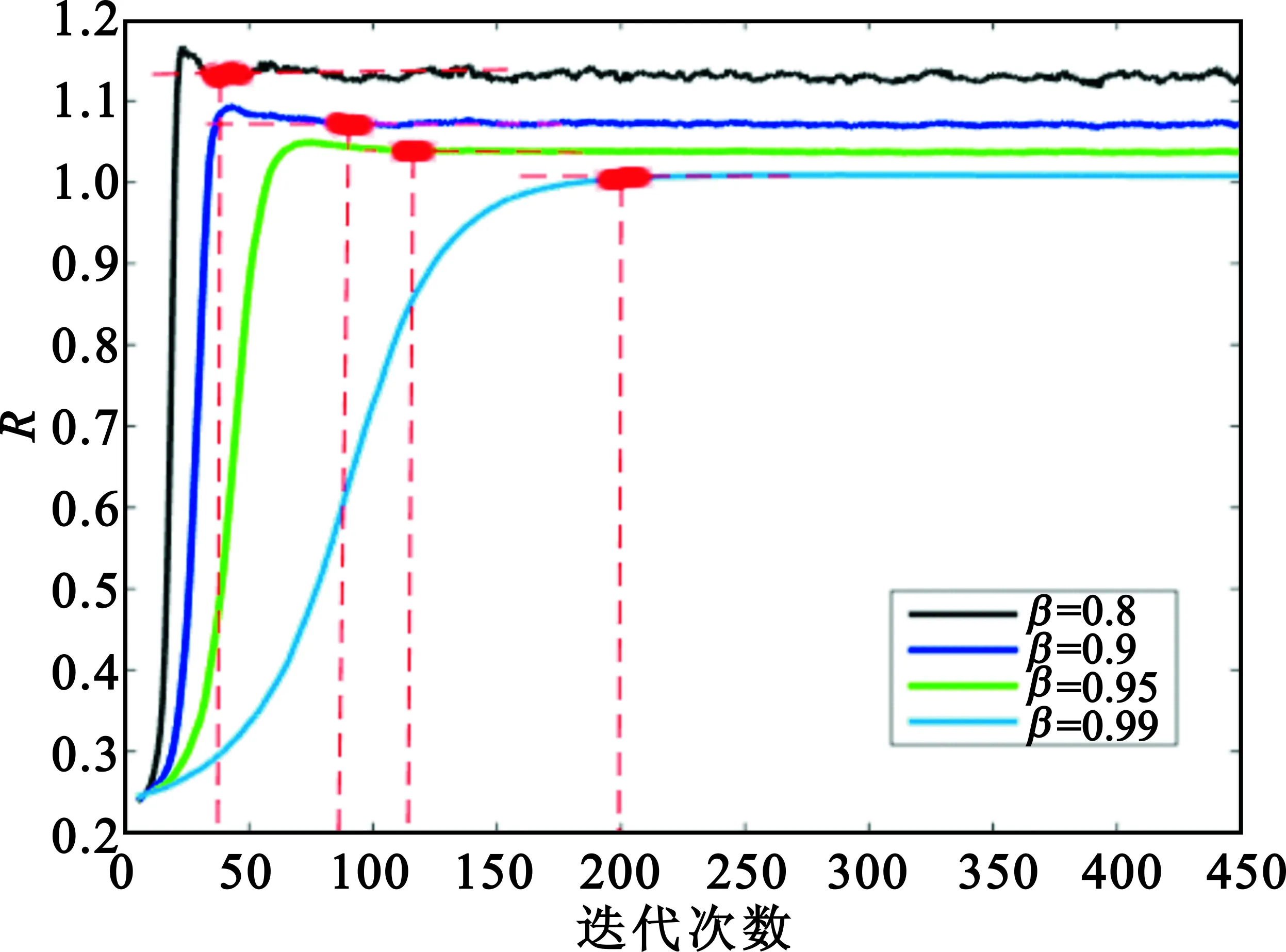
图4 不同遗忘因子下R随迭代变化趋势Fig.4 R changing with different iterations under different forgetting factor

可以看出，在不同遗忘因子下，R的曲线走势相差较大。随着β的增大，R取值收敛所需的迭代次数增大，收敛速度更快；但R的收敛值更趋向于1，且波动范围更小，收敛精度更高，表明收敛速度或收敛精度的提高是以牺牲另一方为代价，所以β取定值时，只能两者间折中处理。通常，在迭代开始时，向量跟踪误差较大，ω需要快速收敛，此时β取值较小；随着迭代进行，向量跟踪误差逐渐变小，ω需要较高的收敛精度，此时β取值较大。

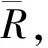
(17)

4.3 迭代停止门限

在缺乏具体应用背景的前提下，PASTd算法并没有设定迭代停止门限，意味着只能通过人工判读迭代是否收敛以及迭代次数，极大限制了算法在实际中的应用。结合DS-SS信号PN码盲估计的应用场景，在迭代过程中，需要实现自动判读是否收敛，及时停止迭代运算，即确定合适的迭代停止门限，从而有效降低计算量，并提高算法的实际应用能力。

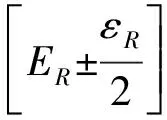
对于非合作接收方，无法后验参数估计精度，但是，基于R与误码率良好的相关性，可以根据预期最低误码率约束参数R收敛后的取值区间，将其作为判断是否收敛以及迭代停止的标准。随着迭代进行，实时计算R在一定迭代次数范围内的统计均值和极差，如果达到迭代收敛门限，则迭代停止；否则，迭代继续进行。

图5和图6分别为100次蒙特卡洛仿真后，估计PN码的误码率和εR随ER的变化情况。

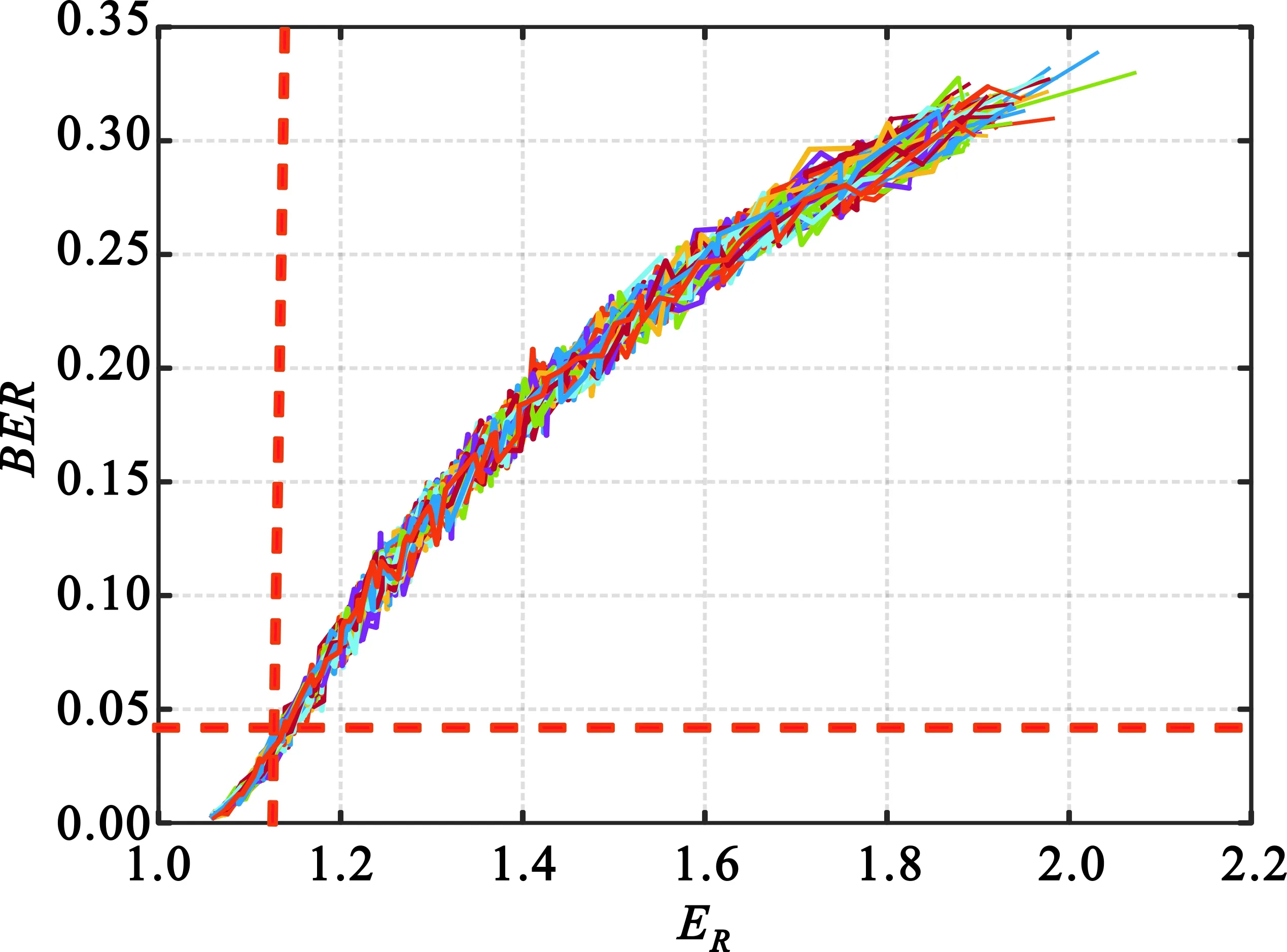
图5 BER随ER变化Fig.5 BER changing with different ER

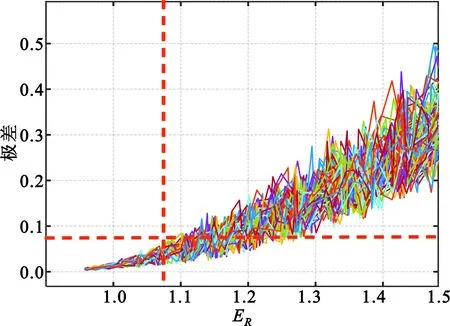
图6 极差随ER变化Fig.6 Range changing with different ER

可以看出，ER与误码率紧密相关，尤其在低误码率时，因此，根据预期最低误码率能够准确约束R收敛后的取值区间；εR虽然随ER变化波动较大，但在约束参数R收敛区间时，εR的作用主要是防止初期迭代时R变化剧烈但统计均值接近收敛，而导致迭代过早停止的情况，所以，对于εR与ER的相关性要求不高。

5 仿真实验与分析

5.1 基于自适应遗忘因子的PASTd算法性能分析

仿真对象：含噪基带DS-SS信号。

仿真参数：采样速率等于码速率，失步时间t0=0，PN码为1 023位的m码，信噪比-10 dB，固定遗忘因子β=0.95，自适应遗忘因子β′基础值μ=0.6。

图7显示了基于自适应遗忘因子和固定遗忘因子下R的迭代变化趋势，标黑区域表示迭代开始收敛。可以看出，相比于固定遗忘因子，基于自适应遗忘因子的PAST算法在达到更优的收敛精度和估计精度的情况下，达到收敛所需的迭代次数降低了接近一半，收敛速度大幅提高，实现了收敛速度和收敛精度的同时优化。

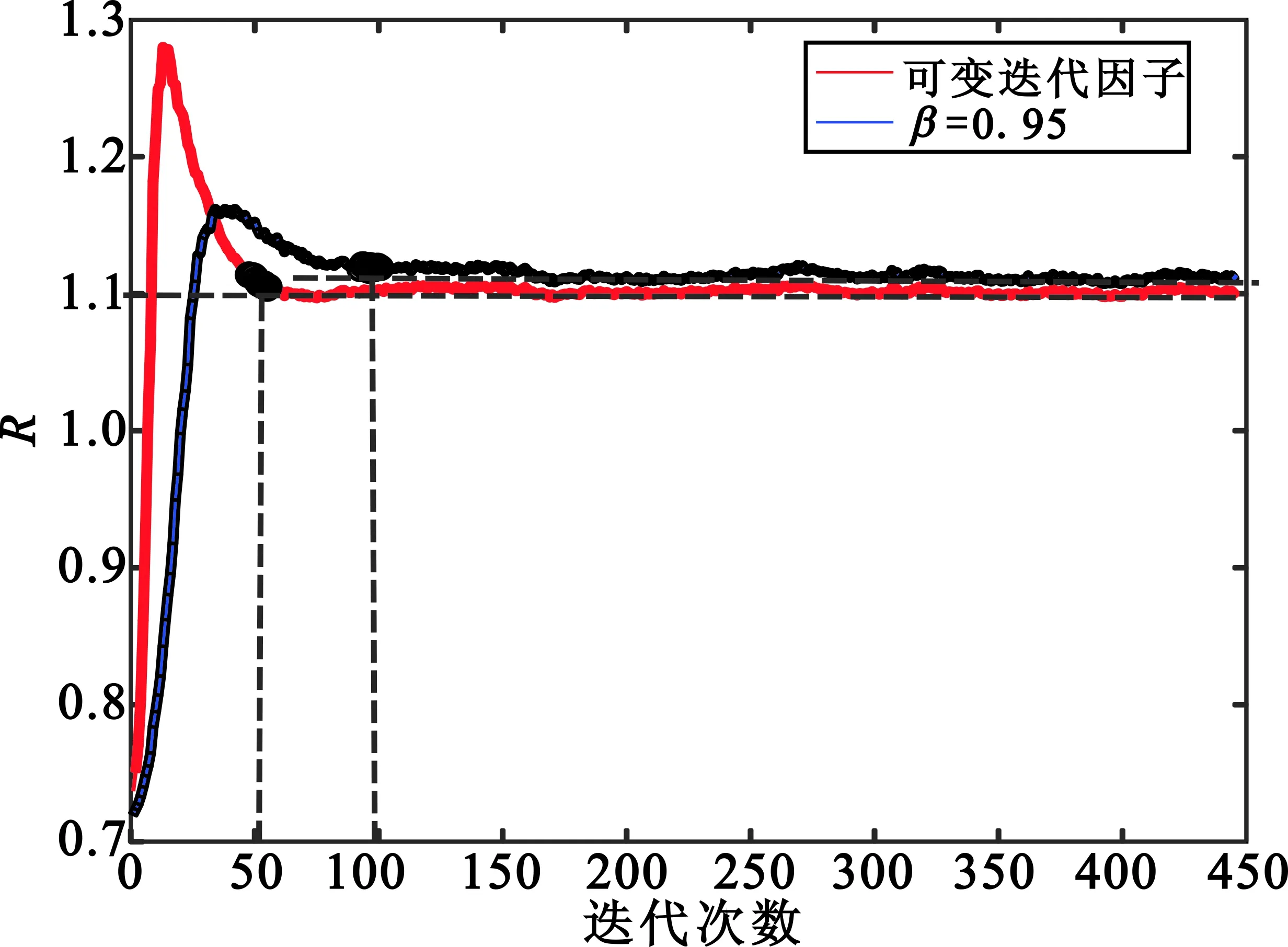
图7 R随迭代变化趋势Fig.7 R changing with different iterations

5.2 迭代停止门限可行性分析

仿真对象及参数参考5.1节，估计PN码的预期误码率不高于5%，取100次蒙特卡洛仿真的统计均值。

图8中蓝色曲线表示了基于4.3节中迭代停止门限的PAST算法在不同信噪比下估计得到的PN码误码率情况，红色曲线则表示了相同信噪比范围下经过500次迭代后(远大于收敛所需的迭代次数)的误码率情况。图9是对应信噪比下自动判别迭代停止时的迭代次数。

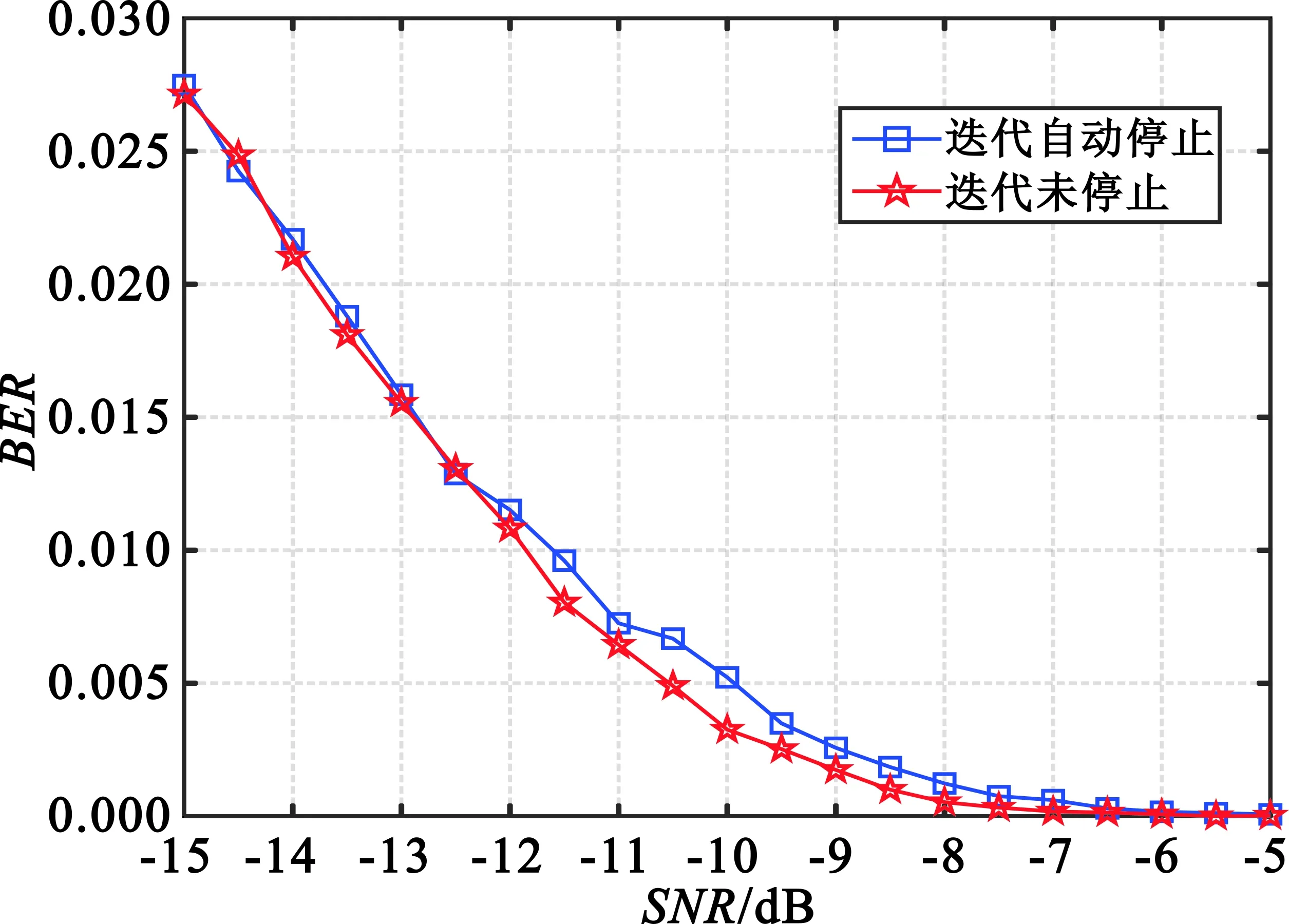
图8 不同信噪比下的BERFig.8 BER under different SNR

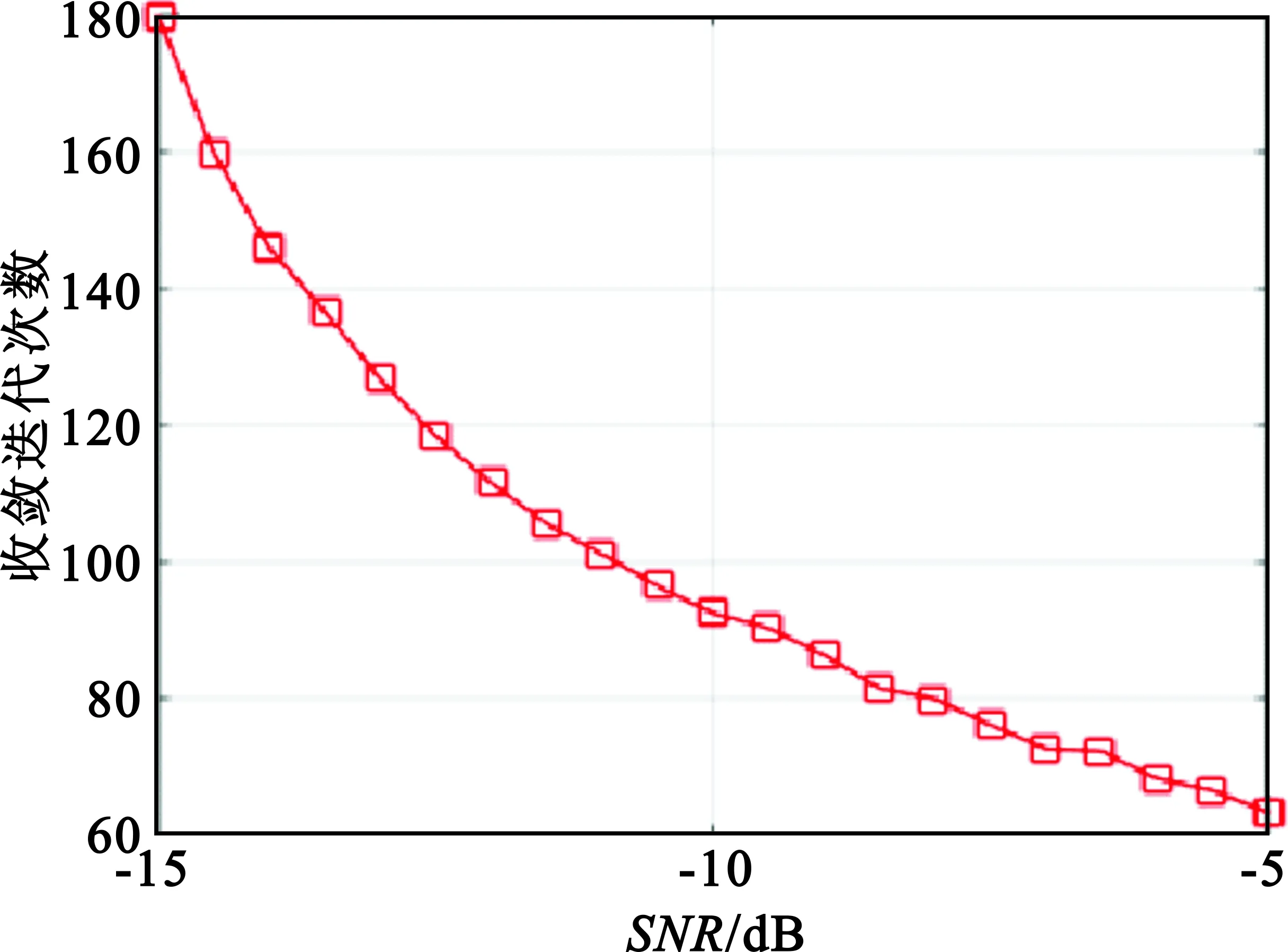
图9 不同信噪比下收敛所需的迭代次数Fig.9 The number of iterations under different SNR

可以看出，基于迭代停止门限自动判别迭代停止得到的估计结果的误码率表现和理想状态下(一定收敛)几乎相等，说明基于4.3节分析设定的迭代停止门限达到了预期目标，即在不牺牲估计精度的前提下实现了迭代收敛的自动判读，而图10中随机抽取的信噪比-10 dB下的仿真情况表明，基于门限对于是否收敛的判读精度甚至优于人工判读，几乎没有增加无谓的迭代次数，有效降低了计算量，提高了算法的实际应用能力。

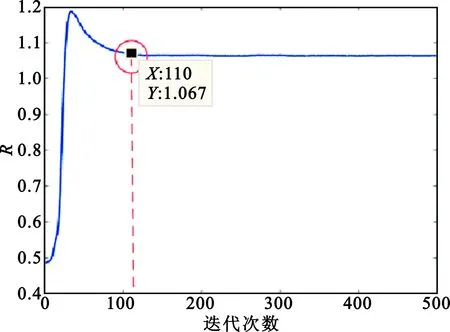
图10 -10 dB信噪比下R随迭代变化趋势Fig.10 R changing with different iterations when SNR=-10 dB

6 结束语

本文提出了一种基于改进的PAST算法实现DS-SS信号PN码盲估计的方法，一方面通过构造基于跟踪误差的自适应遗忘因子，与固定遗忘因子相比，实现了收敛速度和收敛精度的同时优化；另一方面基于收敛精度和估计精度的统计特性，确定了预期最低误码率下的迭代收敛门限，从而在不牺牲估计精度的前提下实现了迭代收敛的自动判读，能够及时停止迭代运算。本文对于传统基于PAST算法的PN码盲估计方法的改进提高了算法实时性数据处理的能力，并解决了算法依赖人工判断收敛的固有限制，但对于扩频比大于1的DS-SS信号，该类方法仍面临因极性模糊导致的PN码估计片段拼接错误的现象。同时，追求更低的信噪比容限也是下一步研究的热点问题。

：

[1] WARTY C,MATTIGIRI S,YU R,et al.Spreading codes for multiuser estimation in non coherent and non cooperative environments[C]//Proceedings of 2013 9th International Wireless Communications and Mobile Computing Conference(IWCMC).Sardinia,Italy:IEEE,2013:1252-1257.

[2] BUREL G,BOUDER C.Blind estimation of the pseudo-random sequence of a direct sequence spread spectrum signal[C]//Proceedings of 2000 Century Military Communications Conference.Los Angeles,USA:IEEE,2000:967-970.

[3] 赵知劲,顾骁炜,沈雷.非周期长码直扩信号的长扰码识别[J].电子与信息学报,2014,36(8):1792-1797.

ZHAO Zhijin,GU Xiaowei,SHEN Lei.An identification method of long pseudo-random code sequence in non-periodic direct sequence spread spectral signals[J].Journal of Electronics & Information Technology,2014,36(8):1792-1797.(in Chinese)

[4] GU X W,ZHAO Z J,SHEN L.Blind estimation of pseudo-random codes in periodic long code direct sequence spread spectrum signals[J].IET Communications,2016,10(11):1273-1281.

[5] 詹亚锋,曹志刚,马正新.DS-SS信号的扩频序列估计[J].电子与信息学报,2005,27(2):169-172.

ZHAN Yafeng,CAO Zhigang,MA Zhengxin.Spread spectrum sequence estimation for DSSS signals[J].Journal of Electronics & Information Technology,2005,27(2):169-172.(in Chinese)

[6] MEHBOOD S,JAMSHID A,FARHANG M.Two algorithms for spread-spectrum sequence estimation for DSSS signals in non-cooperative communication systems[C]//Proceedings of 2016 24th Iranian Conference on Electrical Engineering(ICEE).Okinawa,Japan:IEEE,2016:72-76.

[7] 张红波,吕明.基于子空间跟踪的扩频码盲估计算法[J].系统工程与电子技术,2006,28(10):1470-1472.

ZHANG Hongbo,LYU Ming.Blind estimation of PN spreading sequence based on subspace tracking[J].Journal of Systems Engineering and Electronics,2006,28(10):1470-1472.(in Chinese)

[8] MA C,ZHANG L M,WANG J X.Blind estimation of long code DS-SS signal based on subspace tracking[J].Applied Mechanics and Materials,2014,484:976-981.

[9] GUO L,LYU M,TANG B.Blind estimation of spreading sequence based on neural network by a novel information criterion[C]//Proceedings of 2008 International Conference on Computer and Electrical Engineering.Phuket,Thailand:IEEE,2008:78-81.

[10] 张天骐,赵军桃,江晓磊.基于多主分量神经网络的同步 DS-CDMA 伪码盲估计[J].系统工程与电子技术,2016,38(11):2638-2647.

ZHANG Tianqi,ZHAO Juntao,JIANG Xiaolei.PN code sequence blind estimation of synchronous DS-CDMA based on multi-principal component neural network[J].Journal of Systems Engineering and Electronics,2016,38(11):2638-2647.(in Chinese)

[11] 陆俊.非合作直扩通信信号检测与参数估计方法研究[D].长沙:国防科学技术大学,2011.

LU Jun.Detection and parameters estimation of direct sequence spread spectrum communication signals in non-cooperative context[D].Changsha:National University of Defense Technology,2011.(in Chinese)

[12] 张花国,李鑫,张建华,等.基于半定松弛的长码 DSSS 信号扩频波形估计[J].电子学报,2016,44(2):334-339.

ZHANG Huaguo,LI Xin,ZHANG Jianhua,et al.A semidefinite relaxation approach to spreading waveform estimation for long-code DSSS signals[J].Acta Electronica Sinica,2016,44(2):334-339.(in Chinese)

[13] YANG B.Projection approximation subspace tracking[J].IEEE Transactions on Signal Processing,1995,43(1):95-107.

[14] 张贤达.矩阵分析与应用[M].北京：清华大学出版社,2004:513-517.