受拉钢丝应力状态的磁记忆信号峰峰值判别技术
2018-05-29苏三庆高志刚
苏三庆,高志刚,王 威
(1.西安建筑科技大学 土木工程学院,陕西 西安710055;2. 西安科技大学 建筑与土木工程学院,陕西 西安710054)
钢丝绳作为一种挠性承载机构,由多根钢丝捻制而成,其承载的工作强度高,过载及变形能力强,自重轻,工作状态下噪声小,被广泛应用于煤矿,冶金,石油,建筑等领域[1],同时,钢丝绳在长期的工作情况下还面临磨损、断丝、锈蚀等损害情况,因此,钢丝绳的检测技术应运而生,在这些检测手段中又以电磁检测技术应用最为广泛[1-2],而传统的电磁检测技术以漏磁检测技术最为普遍,但不管是电磁还是非电磁检测技术,只能单纯的判断钢丝绳的损伤情况,却不能反映钢丝绳的承载受力状态,或者是应力应变状况.
磁记忆检测技术作为一种新兴的无损检测技术,在不破坏原有构件结构的基础上,以大地磁场作为励磁源,以磁滞伸缩原理为基础,不仅能够反映构件的损伤情况,而且也能反映构件在受荷条件下的承载及应力应变情况,现已在石油管道,压力容器等领域得到应用[3-6].而钢丝绳用材为低碳冷拔钢丝,因此,有必要针对钢丝绳的特殊材质,探索磁记忆检测技术在钢丝绳领域的应用与发展.
在外力作用下,铁磁体产生磁致伸缩性质的变形,从而引起磁畴壁的位移,这种位移必然引起磁畴的自发磁化方向以增加磁弹性能,来抵消应力能的增加,这种磁状态的不可逆变化在工作荷载消失后会得到保留,记忆着构件应力集中区位置,这就是金属材料的磁记忆效应[7-9].
铁磁体内部或多或少都会存在一些物理不连续现象,当承受荷载时这些部位会产生应力集中,在较大的应力应变条件下,应力能增加,从能量最小的观点出发,此时的磁弹性能增加,磁畴的方向发生改变,并趋于一致[10],此时在铁磁体表面的磁记忆信号便会出现一定的特征变化,典型的特征量为铁磁体表面磁场的法向分量出现过零点现象,而切向分量出现极值.
但磁记忆检测作为一种弱磁检测其影响因素较多[11],比如环境磁场的干扰,加载方向及检测方向的影响,铁磁体材质及形状的影响等等.这些影响因素往往使获取的磁记忆信号并不具有典型的特征.因此有必要针磁记忆检测技术在钢丝绳上的应用做进一步研究.本文以带缺损的钢丝绳单丝为研究对象,以期能找到一种适用于钢丝拉伸破坏的磁记忆判别手段,为下一步整绳的研究做好基础.
2 试验方案
试验选用6×37异形三角股钢丝绳为研究对象,选取其中一股的最外层钢丝进行单轴拉伸试验,钢丝公称直径d=2.7 mm,公称抗拉强度1 670 MPa,钢丝总长400 mm,有效拉伸长度300 mm,检测区域200 mm,在检测区域内设置两处缺口,缺口深度h=0.2 d,宽度w=2 mm,两缺口相聚80 mm,距检测区两端60mm,供选用3根钢丝进行加载,分别编号为:1号试件、2号试件、3号试件,试验在万能拉伸试验机上进行,采用分级加载的方式进行加载,荷载分级为0 kN、2 kN、4 kN、5 kN、6 kN、7 kN、8 kN、9 kN.同时采取保载测量的方式,在目标荷载状态下获取试件表面的磁记忆信号.加载及测量如图1所示.

图1 加载及测量Fig.1 Loading and measuring
在检测区内沿试件纵向设置一条检测线,并且使这条检测线通过两处缺陷,在检测线上设置29个检测点,依次编号为1~29,两处缺陷位置分别位于9点及21点,并在缺陷处设置检测加密区,采用手动测量的方式获取磁记忆信号.在非加密区测点的间距为10 mm,在加密区测点的布置为非等间距,具体布置如图2所示.
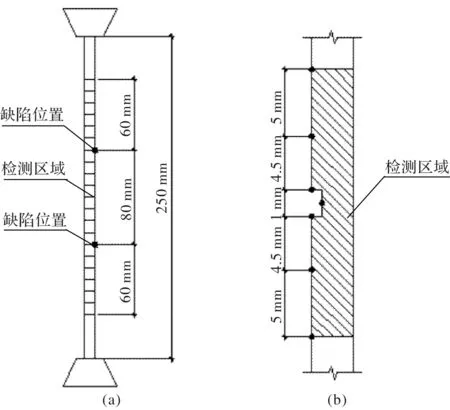
图2 (a)缺陷位置 (b)加密区测点布置Fig.2 (a) Defect position (b) Distribution of test points in dense area
检测装置选用EMS-2003磁记忆/涡流检测仪,如图3所示,探头选用笔式探头,分辨率1 A/m,量程±1 000 A/m,仪器显示设为数显、双踪内时钟,在检测之前进行归一化处理,目的是将连接的探头与大地磁场做校准操作,使仪器与探头相互匹配,校准完成后两通道显示数值为40左右.选用的笔式探头具有屏蔽环境磁场的作用,因设置为双踪,此时CH1显示环境磁场,CH2显示综合磁场,在参数调整选项内选择-CH1,此时的CH1显示为0,CH2数值即为综合磁场减去环境磁场后的磁记忆信号[12].另外检测时保持笔式探头与钢丝垂直,探头紧贴试件表面以减小提离高度的影响,每个测点读取3次磁记忆信号.

图3 检测设备Fig.3 Testing equipment
3 试验现象及结果
三根试验钢丝承载能力相似,都在9~10 kN内拉断,在受荷后的加载阶段可以看出磁记忆信号曲线出现多处波峰波谷,尤其是在缺陷处的两端,波峰波谷贯穿整个加载过程,从开始的波峰波谷不明显阶段,一直到最后钢丝被拉断,波峰波谷现象逐渐趋于明显,其差值也逐渐变大.
在整个加载过程中磁记忆信号基本都为负值,这是由于检测设备在开始检测前进行了归一化处理,这就默认了整个检测过程都是以大地磁场作为基准,而实际的环境磁场是地磁场与周围带磁物体,如机械设备,其他的一些铁磁体等矢量叠加后的结果.同时,钢丝为竖向加载,这与地磁或者说与环境磁场的磁化方向不一致,这就导致了初始条件的相对复杂性.然而实际工程中,检测环境更为多变,待检测构件方向角度、形状,受力情况、环境磁场更为复杂,因此本实验有利于研究复杂条件下的磁记忆信号特征,同时也有必要找到一种适用于复杂条件下的磁记忆检测的判别手段.
三根受测钢丝在相同荷载下磁记忆信号曲线相似,以1号试件为例进行分析.因加密区测点间隔较小,图中很容易出现重叠而不易区分,因此,采用各点等间距作图.
3.1 初始阶段
加载前要先测量钢丝零载条件下的磁记忆信号,以评估钢丝绳初始自带磁场的大小及规律.
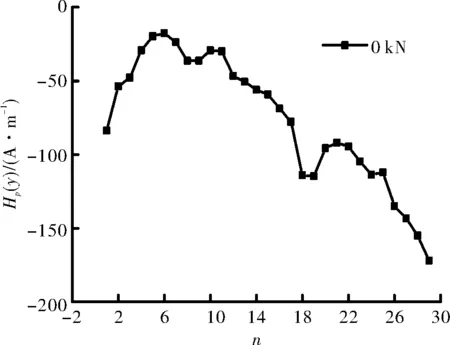
图4 零载对应磁记忆信号曲线Fig.4 The curve of magnetic memory signals at 0 kN
图4中纵轴表示磁记忆信号强度,横轴表示沿检测线由一端至另一端的各检测点编号.
从图中可以看出:磁记忆信号曲线呈现先上升后下降的走势,在6点处存在极大值,也就是说在初始阶段磁记忆信号曲线就存在波峰波谷现象,但波峰波谷数值与相邻点的数值相差不大,值得注意的是两处波谷正好位于9点及21点,也就是说在缺陷处磁记忆信号开始就存在极值,但由于缺陷处极值并不具备明显特征,不好与其他极值区分,因此初始阶段用波峰波谷来判断缺陷位置还不具说服力.同时零载阶段磁记忆信号并没有太大幅度的跳跃,这也说明初始阶段钢丝自带磁场稳定,有利于下一步的检测.
3.2 缺陷处非线性段形成阶段
进入加载阶段后磁记忆信号曲线在缺陷两端逐渐形成波峰波谷,在缺陷处出现平滑的非线性平台.波峰波谷数差值逐渐增大,位置由最初的远离缺陷到逐渐靠近缺陷处发展.
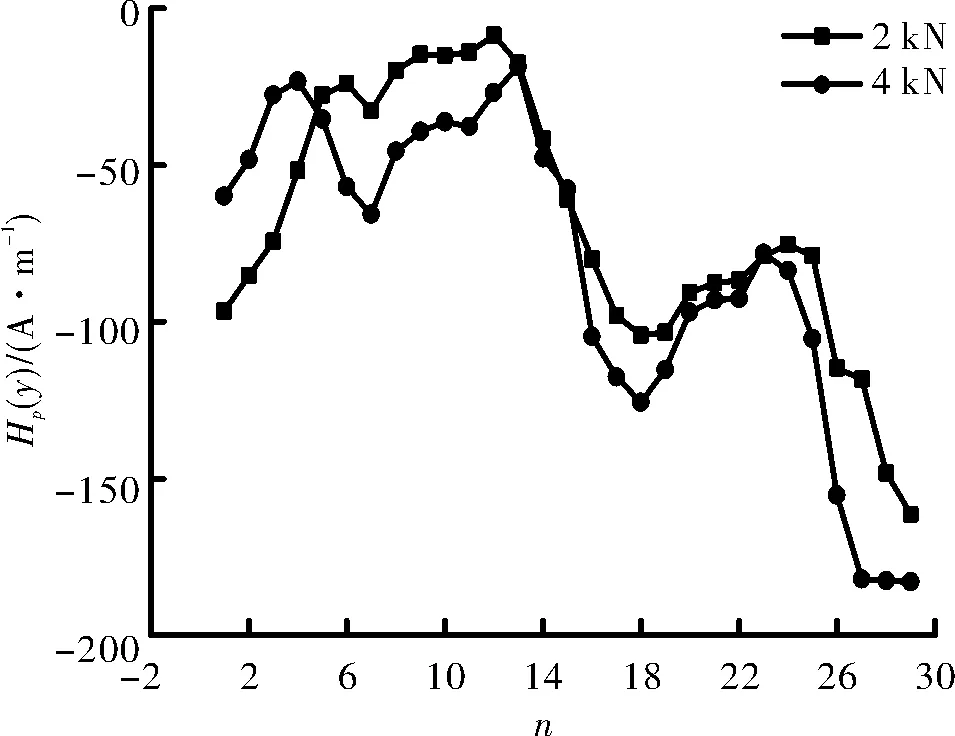
图5 2 kN、4 kN对应磁记忆信号曲线Fig.5 The curve of magnetic memory signal at 2 kN,4 kN
由5图可知:在承受荷载后,磁记忆信号曲线波峰波谷现象更加明显,波峰波谷差值进一步增加.在2 kN对应荷载下9点缺陷两端的波峰波谷出现在7和12点之间,21点缺陷两端的波峰波谷出现在18和24点之间;在4 kN对应荷载下9点缺陷两端的波峰波谷出现在7和13点之间,21点缺陷两端的波峰波谷出现在18和23点之间.具体位置及数值如表1和表2所示.

表1 2 kN对应位置及数值
注:上表位置栏括号内数字表示测点编号

表2 4 kN对应位置及数值
注:上表位置栏括号内数字表示测点编号
同时在波峰波谷之间出现平缓的非线性平台,且非线性平台都出现在缺陷位置,如2 kN时对应的非线性平台为8~10点区段以及20~22点区段,4 kN时非线性平台出现在8~11点区段及20~22点区段.缺陷处的应力水平相对于其他部位要高得多,应力的增加会导致磁导率的变化,同时应力导致应变的增加,在局部应变较大的情况下,磁畴偏转会进一步加剧,这就相当于在原有磁场的基础上附加了一个磁场[13],因此在这个部位磁记忆信号曲线会出现与相邻部位不一样的变化.
3.3 波峰波谷进一步加剧阶段
随着荷载的进一步增加,波峰波谷数值之差进一步加剧,在9点缺陷处仍然存在非线性段,而缺陷21点处已不是很明显,同时波峰波谷位置发生变化,但总体趋势相差不大(图6),其数值及位置如表3—表5所示.
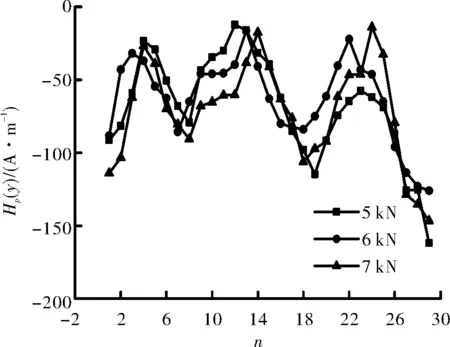
图6 5 ~7 kN对应磁记忆信号曲线Fig.6 The curve of magnetic memory signal at 5~7 kN

位置/mm数值/(A·m-1)位置/mm数值/(A·m-1)波峰80(n=12)-12.33155(n=23)-57.67波谷69.5(n=8)-79.33145(n=19)-114.67差值11671057
注:上表位置栏括号内数字表示测点编号

表4 6 kN对应位置及数值
注:上表位置栏括号内数字表示测点编号
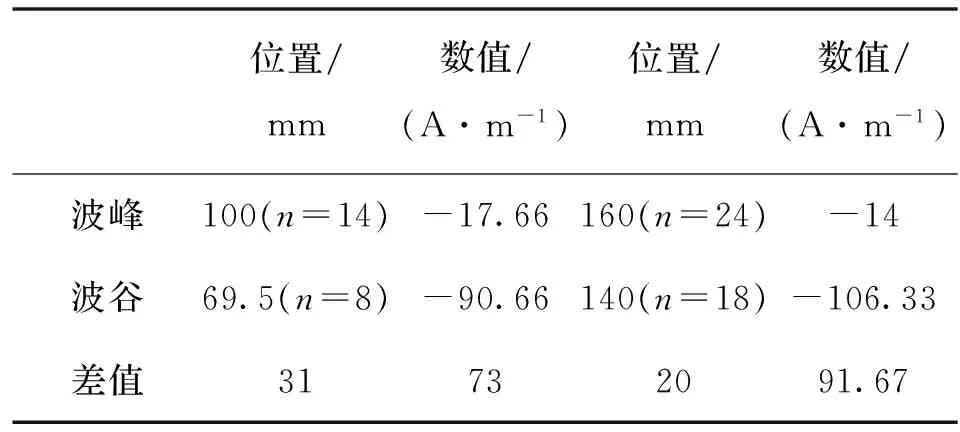
表5 7 kN对应位置及数值
注:上表位置栏括号内数字表示测点编号
从表中可看到:不管是9点两端的波峰波谷之差值还是21点两端的波峰波谷之差值,都呈现单调递增的趋势,而波峰波谷位置距离则没有明显规律.荷载的进一步增加,磁记忆信号曲线规律性更加明显,应力应变的增加导致应力能的增加,进而引发磁弹性能的增加,磁畴的翻转及畴壁的位移加剧,磁化方向趋于稳定.因此3条磁记忆信号曲线走势相同,规律明显.
3.4 非线性段消失阶段
荷载加至8 kN和9 kN后,波峰波谷间的非线性段消失,缺陷处表现出了良好的线性关系,同时波峰波谷数值之差进一步增大,间距也开始减小,两条曲线走势基本相同尤其是在21点缺陷处,磁记忆信号曲线出现重叠,这说明随着应力的增加磁畴的翻转及磁畴壁的位移已达到饱和(图7).
值得注意的是当荷载达到9 kN后21点左右两点正好为波峰波谷位置,根据下式计算梯度发现20到22三点间的梯度数值最大.分别为61.667×103A/m2和44.66×103A/m2.
(1)
8 kN和9 kN 时波峰波谷位置及数值如表6和表7.
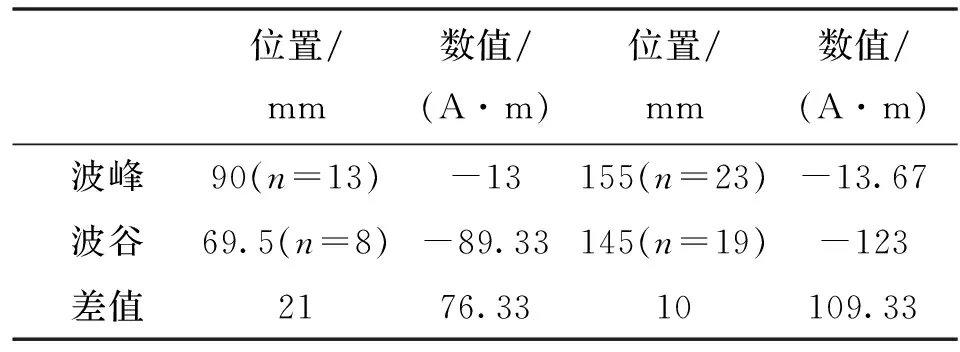
表6 8 kN 对应位置及数值
注:上表位置栏括号内数字表示测点编号

表7 9 kN对应位置及数值
注:上表位置栏括号内数字表示测点编号
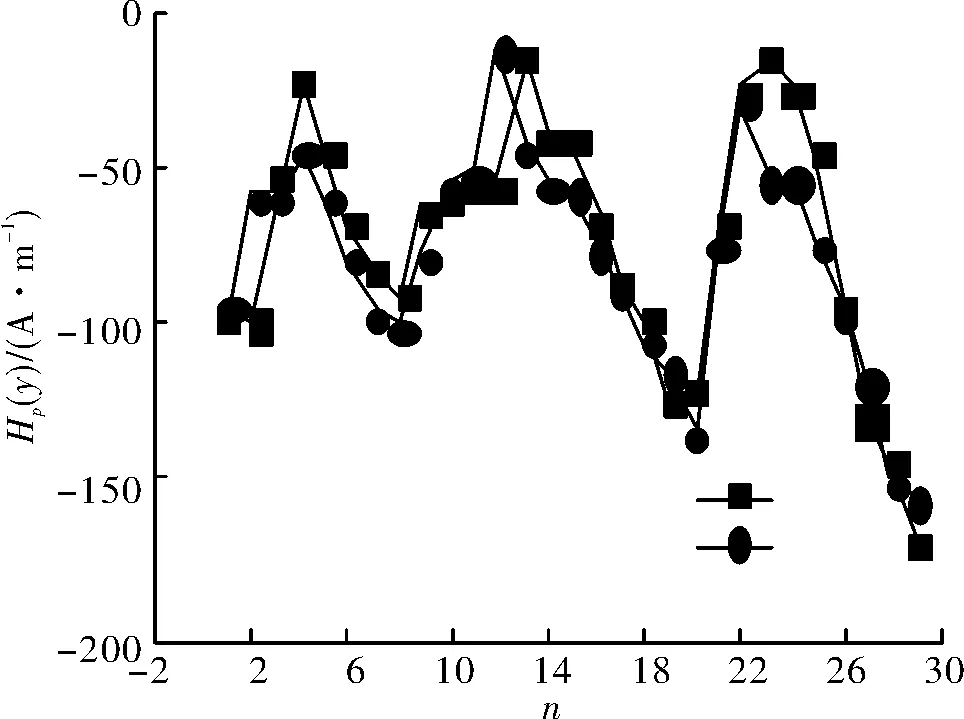
图7 8 kN,9 kN对应磁记忆信号曲线Fig.7 The curve of magnetic memory signal at 8 kN,9kN
3.5 破坏后
试件最后在21点处破坏,表现为突然间的脆性破坏,最终破断拉力为9.18 kN,此时的磁记忆信号只存在一组波峰波谷,即20点和21点,同时在21点处出现过零点现象,峰值的绝对值出现较大幅度的增长,曲线在端口两端平滑(图8).
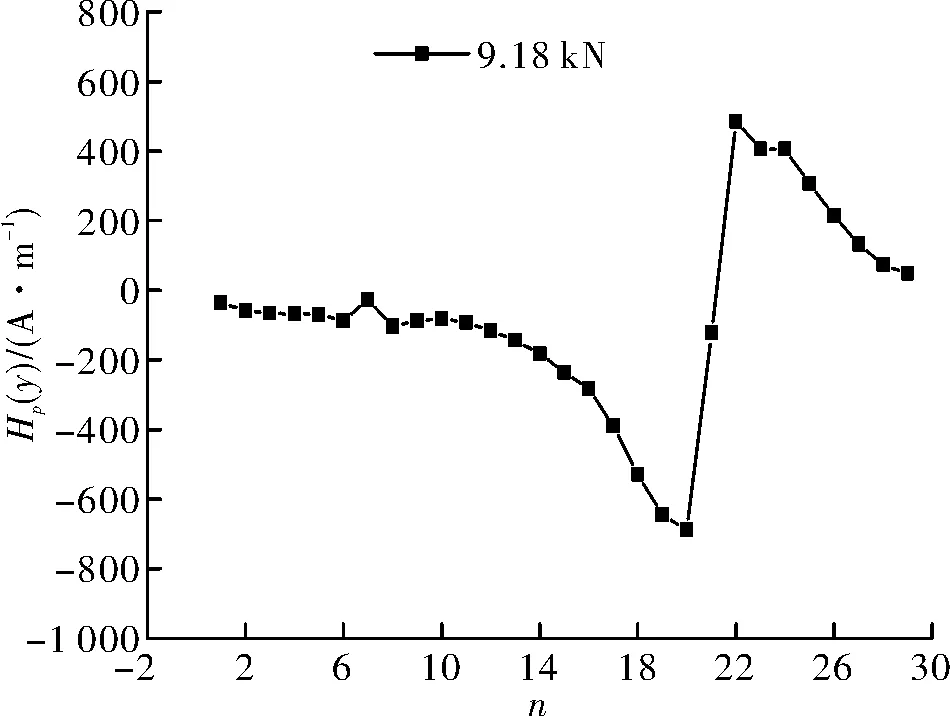
图8 破坏后磁记忆信号曲线Fig.8 The curve of magnetic memory signal after failure
4 分析与讨论
4.1 试验现象分析
磁记忆检测的一般判别理论及标准认为:磁化强度与应力应变存在一定的关系[15],在应力集中位置,较高的应力水平,会导致内部磁畴的排列以及磁化方向发生变化,这些重新取向的磁畴会使得外部漏磁出现规律性的特征,即法向分量Hp(y)过零点,而切向分量Hp(x)出现极值[14],从各级荷载的磁记忆信号曲线来看,磁记忆信号基本为负值,只有在最后拉断的磁记忆信号曲线中出现过零点,而由经典的磁偶极子模型也认为在应力集中处法向分量出现过零点.但这也仅是一种理想的判别技术,本次试验采用竖向拉伸即试件方向为竖向放置,与地磁方向垂直,同时试件周围的环境磁场是地磁与其他干扰磁场矢量合成的结果,因此其大小方向很难判断,为减小误差,测量前对仪器进行了归一化处理,这本身就是一种简化处理,而在实际应用中,磁场更为复杂,因此有必要找到一种适用于实际现场的判别手段(图9).
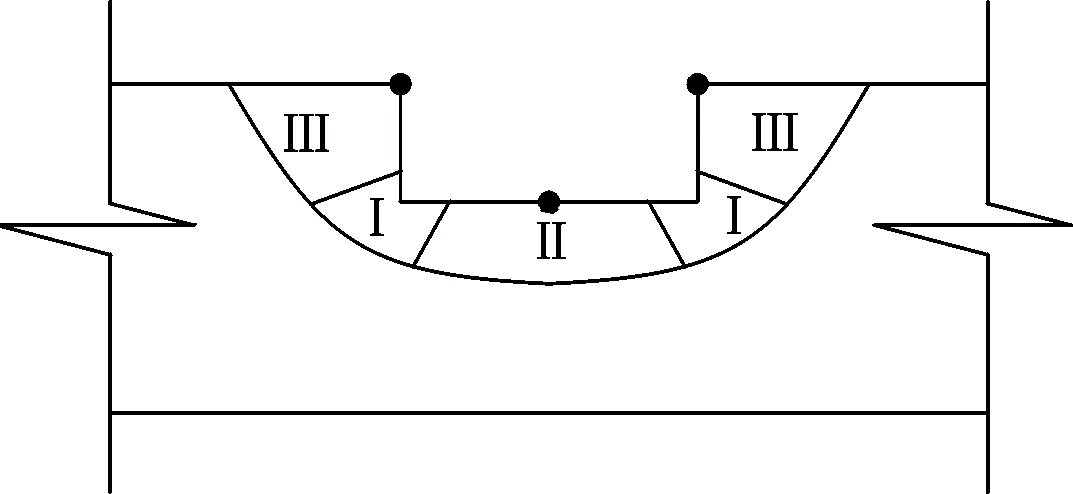
图9 应力分区Fig.9 Different stress distribution
磁记忆检测技术可看成是一种漏磁检测,但这种检测技术又与被测构件的应力应变有关,应力应变小的部位其磁畴偏转畴壁移动幅度轻微,而在应力应变较大的位置磁畴偏转剧烈,分析钢丝缺陷位置可将缺陷位置处划分为三种应力状态.
Ⅰ区为应力集中区,为应力最大部位,Ⅱ区为偏心受拉部位,Ⅲ区为无应力或应力微小部位,黑点为测量点,因磁记忆信号与应力存在对应关系,而Ⅲ区和Ⅱ区应力存在较大偏差,因此,其磁记忆信号也应存在差距,而从各级荷载的磁记忆信号曲线来看:在荷载很小的时候缺陷处的应力相差不大,但当荷载发展至一定阶段各区应力出现偏差,此时磁记忆信号曲线缺陷处的波峰波谷现象明显,同时缺陷处的磁记忆信号也恰好位于波峰波谷之间,即缺陷处的磁记忆信号与两端波峰波谷的数值之差开始加剧,由于试验钢丝相较于探头较细,因此测量存在一定偏差,但磁记忆信号曲线已经足以反应应力与磁记忆信号存在对应关系,同时根据法向分量过零点的判别依据可知,在应力集中部位磁记忆信号曲线存在单调递减或递增段,这也与试验得到的磁记忆信号曲线相符.
4.2 基于磁记忆的钢丝应力状态判别技术
由上述分析可知:可通过不同部位磁记忆信号的差值对应这些部位的应力进行判断,即梯度曲线可反映应力应变的对应关系,但由于磁记忆信号曲线在缺陷处存在非线性平台,在此区段内的梯度数值较小,容易与其他处的梯度值产生混淆.仅仅是在最后8 kN,和9 kN时缺陷处的磁记忆信号的梯度值在21点最大,因此梯度曲线适合对最后频临破坏阶段进行判别.考虑到应力与磁信号的对应关系,与其用缺陷处磁记忆信号与两端波峰波谷分别做差,不如用波峰波谷数值之差来反映波峰波谷区段内的应力变化程度.
不考虑初始状态即零载以及拉断后的磁记忆信号,将2 ~ 9 kN对应缺陷处两端的波峰波谷数值之差绘制成曲线如图10.其中:
ΔHp(y)=Hp(y)c-Hp(y)t
(2)
Hp(y)c为波峰处磁记忆信号数值;Hp(y)t为波谷处磁记忆信号数值.
不管是9点处波峰波谷差值曲线还是21点处波峰波谷差值曲线,都呈现很好的增长趋势,只有21点处的波峰波谷差值曲线在9 kN时出现下降,但下降量很小,两条曲线均可分为三段,9点处的峰值差值曲线表现出很好的线性,可看成是三段折线组成,分界点为3点和6点,对应荷载为5 kN和8 kN,21点处的峰值差值曲线虽没有很好的线性规律,但各段分界明显,也可近似看做三段折线组成,分界点为4点和8点,对应荷载为6 kN和8 kN.观察发现拉断后21点处出现径缩现象,应变突然增大,而9点处变化不大,应变的急剧增加,会进一步加剧构件内部缺陷的发展,晶格排列进一步错乱,位错加剧,这也会导致磁场的不规律变化,因此9点处的峰值差值曲线与21点处的峰值差值曲线会出现一定差异.
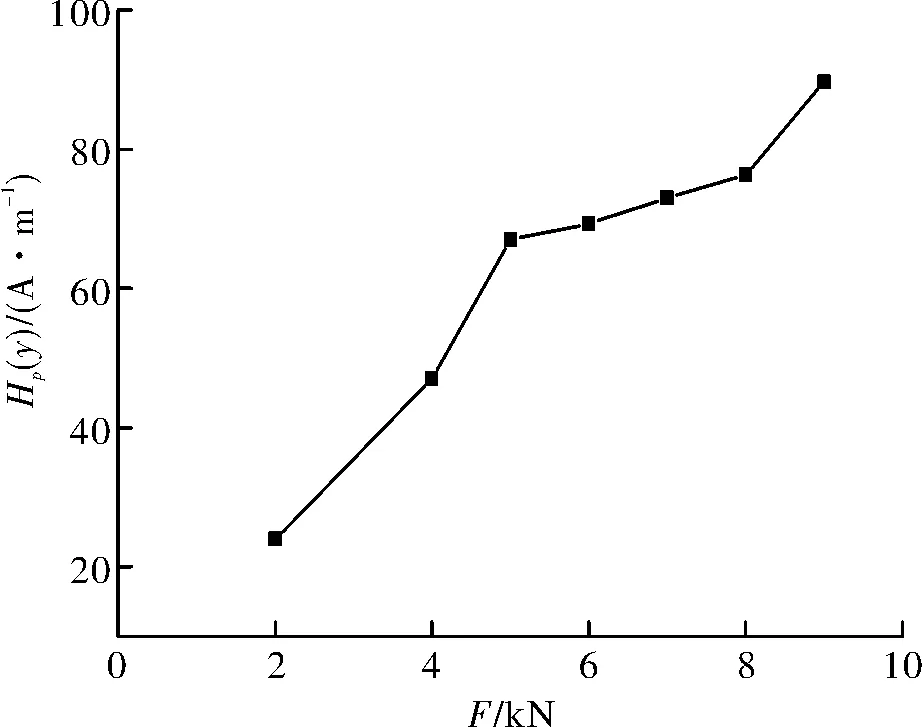
图10 9点两端对应波峰波谷差值曲线Fig.10 Difference curve of peaks and valleys corresponding the both ends at 9 point
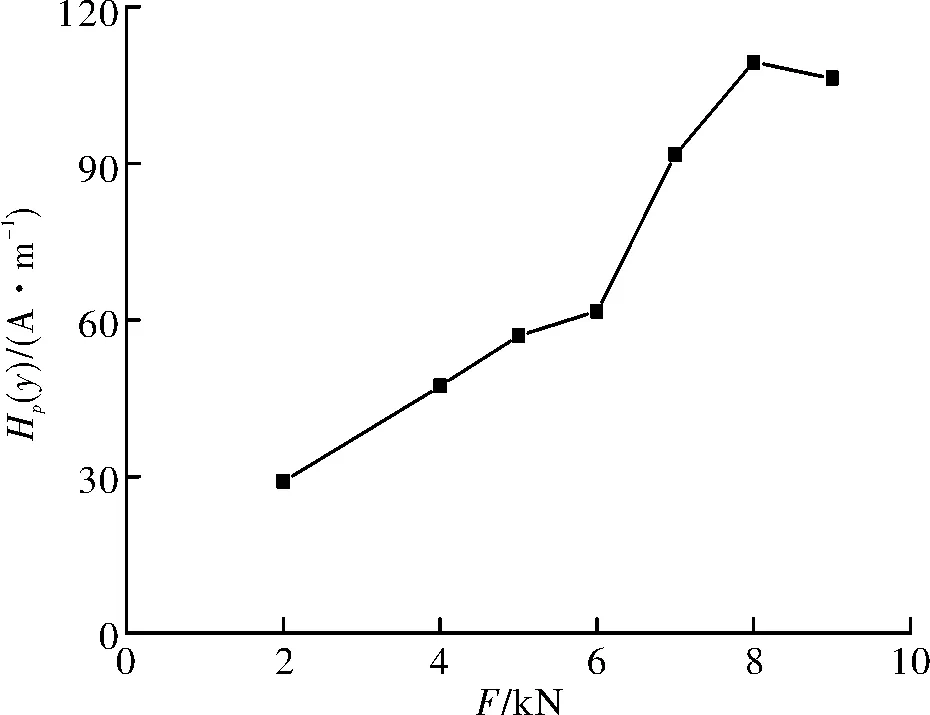
图11 21点两端对应波峰波谷差值曲线Fig.11 Difference curve of peaks and valleys corresponding the both ends at 21 point
波峰波谷的差值曲线的三个阶段可作为反应磁记忆信号发展的三个阶段,根据实际需要可将三个阶段的分界点作为控制点,若对试件的强度储备要求高,可以将第一段和第二段的分界点作为一个预警值,若对试件的强度储备要求不高者可将第二段和第三段的分界点作为预警点,这样不仅可以对应某一荷载的应力应变状况,还可以作为从零载到破坏整个加载阶段的过程控制曲线.
因此磁记忆信号波峰波谷差值曲线可作为一种全过程的判别手段.
5 结论
(1)磁记忆信号曲线随着荷载的增加,在缺陷处两端出现波峰波谷现象,拉断后在断点处出现波峰波谷,同时磁记忆信号曲线在缺陷处出现非线性平台,当荷载增加至8 kN时,非线性平台消失.
(2)随着荷载的增加波峰波谷的数值之差为递增状态,但在缺陷处没有出现过零点现象,只有拉断后才在断点处出现过零点,因此过零点现象仅仅适用于破坏后的试件判别,很难作为整个受力过程的判别技术.
(3)可将波峰波谷差值曲线作为磁记忆检测技术应用于钢丝的判别手段,波峰波谷差值曲线可作为反应试件受力全过程的判别曲线.
(4)缺陷处不同部位的应力差距可通过磁记忆信号曲线的峰峰值做出反映.应力与磁记忆信号存在对应关系.
[1] 牟帅, 陈志平. 钢丝绳无损检测技术研究进展[J]. 机电工程, 2014,31(6):707-710.
MOU Shuai, CHEN Zhiping. Progress on nondestructive testing technology of wire ropes[J]. Journal of Mechanical & Electrical Engineering, 2014,31(6):707-710.
[2] 李光远. 基于电磁法的钢丝绳无损检测技术的研究[D].北京:北京邮电大学, 2014.
LI Guangyuan. Research of the wire rope nondestructive testing technology based on electromagnetic method[D]. Beijing: Beijing University of Posts and Telecommunications, 2014.
[3] DOUBOV A. A.. Diagnostics of equipment and constructions strength with usage of magnetic memory inspection[J]. Diagnostics, 2011,35(6):19-29.
[4] DOUBOV A. A., DEMIN E. A., MILYAEV A. I., et al. The experience of gas pipeline stress-strain state control with usage of the metal magnetic memory method as compared with conventional methods and stress control means[J]. Welding in the World, 2002, 46(9-10):29-33.
[5] 王威. 基于磁记忆漏磁特性的钢结构构件潜在损伤早期诊断的基本理论及应用技术研究[R]. 上海:同济大学博士后研究工作报告, 2008.
WANG Wei. The basic theory andapplication of NDT&E based on metal magnetic memory and magnetic flux leakage testing for initial potentially damage of steel structural member[R]. Shanghai: Tongji University Post-Doctoral Research Work Report, 2008.
[6] DOUBOV A A. A study of mental properties using the method of magnetic memory [J]. Mental Science and Heat Treatment, 1997,39(9/10):401-402.
[7] 任吉林, 林俊明, 任文坚,等. 金属磁记忆检测技术研究现状与发展前景[J]. 无损检测, 2012, 34(4):3-11.
Ren Jilin, LIN Junming, REN Wenjian, et al. Metal magnetic memory testing technology development status and prospect[J]. NDT,2012,34(4):2-10.
[8] 任吉林, 邬冠华, 宋凯,等. 金属磁记忆检测机理的探讨[J]. 无损检测, 2002, 24(1):29-31.
Ren Jilin, WU Guanhua, SONG Kai, et al. Study on the mechanism of metal magnetic memory testing[J].NDT, 2012,34(4):2-10.
[9] 邢海燕, 徐敏强, 李建伟,等. 磁记忆检测技术及工程应用[M]. 北京:中国石化出社, 2011.
XIN Haiyan, XU Mingqiang, LI Weijian, et al. Magnetic memory Testing Technology and Engineering Application[M].Beijing: China Petrochemical Press,2011.
[10] 任吉林,林俊明.电磁无损检测[M]. 北京:科学出版社, 2008.
REN Jilin, LIN Junming. Electromagnetic nondestructive testing[M]. Beijing: Science Press, 2008.
[11] 苏三庆, 孙灏江, 王威, 等. 弯曲荷载作用下焊接钢板件金属磁记忆效应试验研究[J]. 西安建筑科技大学学报(自然科学版), 2017,49(6):771-776.
SU Sanqing, SUN Haojiang, WANG Wei, et al. Experimental research on metal magnetic memory effect of butt welded steel plate under bending load[J]. J. of Xi′an Univ. of Arch. & Tech.(Natural Science Edition), 2017,49(6): 771-776.
[12] 苏三庆,马小平,王威,易术春,路秀琪,任广超,牛晓波.基于ANSYS有限元模拟的钢丝绳单丝拉伸力-磁耦合研究[J].西安建筑科技大学学报(自然科学版),2017,49(3):309-316,331.
SU Sanqing, MA Xiaoping, WANG Wei, et al. Research on magneto-machanical coupling on tensile monofilament steel wire rope based on ANSYS finite element simulation[J]. J. of Xi′an Univ. of Arch. & Tech.(Natural Science Edition), 2017,49(3):309-316,331.
[13] 王正道, 姚凯, 沈恺, 等. 金属磁记忆检测技术研究进展及若干讨论[J]. 实验力学, 2012, 27(2):129-139.
WANG Zhengdao, YAO Kai, SHEN Kai, et al. Advances and evaluation of metal magnetic memory NDT technique[J]. Journal of Experimental Mechanics, 2012, 27(2):129-139.
[14] 曾发荣, 王威, 易术春, 等. 基于建筑钢结构拉伸试验磁记忆检测研究[J]. 钢结构, 2015, 30(1):25-28.
ZENG Farong, WANG wei, YI Shunchun, et al. Study of magnetic memory testing based on tensile test of building steel structure[J]. Steel Construction, 2015, 30(1):25-28.
[15] 王威, 任广超, 苏三庆, 等. 钢梁弯曲应变与磁记忆效应的关系研究[J]. 西安建筑科技大学学报(自然科学版), 2017,49(1):29-35.
WANG Wei, REN Guangchao, SU Sanqing, et al. Research on the relationship between flexural strain and metal magnetic memory for steel beam[J]. J. of Xi′an Univ. of Arch. & Tech.(Natural Science Edition), 2017,49(1):29-35.
