混凝土SHPB试验端面摩擦效应研究

李晓琴，陈前均，陈保淇，陶 毅

(1.昆明理工大学 建筑工程学院，云南 昆明 650000；2.上海市工程结构安全重点实验室，上海 200000；3.西安建筑科技大学 土木工程学院，陕西 西安 710055)

混凝土材料通常应用在各类民用及公共设施和国防建设中.混凝土是应变率敏感性材料，混凝土结构遭受由地震或恐怖袭击等突发事件引起的冲击或爆炸荷载时，依旧采用混凝土静态力学参数进行结构动力分析将不能准确预测其动态响应.一般引入动力增强因子(Dynamic Increasing Factor，简称DIF)用于量化应变率对混凝土强度的增强效应，DIF为动态强度与准静态强度的比值，该值为混凝土准静态抗压或抗拉强度和应变率的函数[1].

目前，针对混凝土材料动态抗压强度的增强效应，已经有大量的试验研究[2-12].Bischoff 和Perry[2]通过试验认为混凝土材料的强度随着应变率增加而增强的现象是由多种因素造成的，比如：试验方法、试件尺寸、材料属性(主要是混凝土静态抗压强度)、骨料尺寸、边界效应以及侧向惯性效应等.Zhang等[3]通过SHPB对混凝土圆环试件进行试验，证明了动态混凝土抗压强度增强效应的增加主要来源于惯性约束作用的影响，即混凝土在动荷载作用下径向膨胀变形滞后于加载速率导致的强度增加的现象.另有研究认为，应变率在1 s-1以内时，混凝度的强度增强效应主要是由自由水Stefan效应[4]导致的，主要表现为同一静态抗压强度的混凝土在相同应变率条件下湿混凝土的动态强度增量显著高于干混凝土的强度增量.而当应变率超过10 s-1时，大量研究表明混凝土强度的增加主要是由于侧向惯性约束的影响[5-9].其中Li和Meng[5]，Kim[8]和Li等[9]认为除了侧向惯性约束效应之外，端面摩擦效应是导致混凝土动态强度增加的另一个重要因素.端面摩擦效应即由于混凝土试件表面粗糙，试件径向膨胀变形受到约束，从而导致其强度增强的效应.为减少端面摩擦效应，目前试验处理的方法一般为在试件表面涂抹润滑剂，此方法对于金属SHPB试验可以取得很好的效果，但是，对于混凝土动态抗压SHPB试验，由于其表面的粗糙程度远远大于金属试件，试验过程中不可能完全忽略端面摩擦效应的影响[5].Klepaczko等[10]研究发现混凝土SHPB试验中，当试件的长径比设置成1，同时对SHPB杆和混凝土试件的界面进行充分润滑，即摩擦因数μ= 0.02 ～ 0.06时端面的摩擦效应可以不予考虑.然而在实际试验中，即使在端面充分涂抹润滑剂也很难达到Klepaczko等[10]提出的摩擦因数的取值范围[11].Li和Meng[5]对SHPB试验进行了数值模拟研究，分析了端面摩擦效应的影响，发现当μ取值小于0.1时，端面摩擦效应对DIF的影响很小；但当μ取值超过0.2时，端面摩擦效应对DIF有着重要影响.同样Mu等[12]通过数值模拟研究发现端面摩擦效应在混凝土的应变率超过68 s-1之前对DIF有重要影响.

虽然现有研究[5-12]肯定了端面摩擦效应对DIF的重要影响，但是其影响的具体量值尚未有详细讨论和量化.本研究基于LS-DYNA显示分析，利用其材料库中的K&C局部损伤混凝土模型[13]，对混凝土动态抗压SHPB试验进行数值模拟，通过对混凝土与SHPB杆接触界面设置不同的摩擦因数μ，分析了混凝土端面摩擦效应对DIF的影响，完成了对混凝土动态抗压SHPB试验端面摩擦效应的定量分析.并基于SHPB二波法理论重构了混凝土试件在不同应变率条件下的抗压应力应变曲线，分析了混凝土试件在不同应变率下的破坏规律.

1 混凝土SHPB试验测量抗压DIF原理

目前，在应变率范围为10～ 103s-1时，SHPB试验常被用于混凝土动态抗压强度和DIF的测量[5]，试验装置如图1所示，包括五部分.试验开始时，子弹按一定速度撞击输入杆，将在输入杆端产生一个入射应变脉冲εⅠ(t)，之后该脉冲由输入杆传播到试件中，试件在应力脉冲作用下发生变形，并在输入杆与试件的界面产生反射脉冲εR(t)返回输入杆，另一部分透射脉冲εT(t)穿过试件进入输出杆.在输入杆与输出杆上分别粘贴有电阻应变片，用于记录应变脉冲时程数据，之后依据该时程曲线可以计算得到混凝土的动态抗压强度和相应的应变率，进而可以确定DIF与应变率的关系，其中动态抗压强度和应变率的计算公式如下：

(1)

(2)

(3)

式中：E为SHPB杆弹性模量；A0为SHPB杆截面面积；AS为混凝土试件截面面积；lS为混凝土试件初始长度；C0为SHPB杆中的弹性波波速，其计算公式如下：

(4)

式中：ρ为SHPB杆密度.按式(1)和式(2)可以重构混凝土动态抗压应力应变曲线.

图1 试验装置Fig.1 Test device

2 不考虑端面摩擦效应的SHPB抗压有限元模拟

2.1 混凝土动态抗压DIF

随着应变率的上升，混凝土的动态抗压强度增加，已有的大量试验研究中给出了多种DIF与应变率的函数关系[5-10].目前，普遍采用的DIF应变率公式是CEB公式[14]，其数据基于不同强度等级的混凝土试验，应变率变化范围为30×10-6～ 300 s-1，具有广泛的适用性，其计算公式如下：

(5)

γs=10(6.156αs-2)

(6)

αs=1/(5+9fcs/fco)

(7)

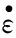
2.2 混凝土模型选择及SHPB模型建立

在利用有限元研究混凝土结构受动态荷载作用下的动力响应时，目前混凝土材料一般采用RHT，K&C，HJC等模型[15].HJC模型基于多孔材料的三段式状态方程描述混凝土压力与体积应变的关系，未考虑应力偏张量中第三不变量的影响.Tu和Lu[15]采用RHT模型和K&C模型分别模拟了爆炸荷载作用下的混凝土板的动力响应，结果表明：RHT模型无法反映混凝土三轴受拉时的脆性特质，且用AUTODYN默认的参数值作数值模拟将造成应变软化段下降缓慢与实验结果不符；而K&C模型应变软化段的计算结果与试验结果更加吻合.因此，本文选用K&C模型[13]进行混凝土材料的有限元建模.

K&C材料模型可以通过在材料卡片中自定义DIF和应变率的关系曲线来考虑材料应变率效应.DIF曲线[14]是通过SHPB试验数据回归得到，而其本质也是高应力波作用下混凝土材料在SHPB试件尺度下的宏观效应的体现，并非绝对的混凝土材料本身的应变率效应.目前，已有研究证明混凝土SHPB抗压试验DIF的来源主要源自结构效应而并非材料自身的增强效应[5-8]，因此，如果盲目引入宏观试验结果回归所得的DIF曲线来定义混凝土材料属性将会高估混凝土试件的动态材性.其次，引入DIF曲线还需要考虑局部损伤混凝土模型在高应变率下网格收敛性和应变率敏感性[16]等尚未讨论清楚的问题.因此，本文所有数值模拟计算都没有在K&C模型中定义DIF与应变率的关系曲线.

本次有限元模拟采用的试验原型以Li和Meng[5]的试验试件为依据，试件的具体参数见表1.SHPB试验装置的有限元模型中，各部分均采用Solid 164三维8节点常应力实体单元类型，对fcs=40 MPa的混凝土试件进行数值模拟.因为该模型具有对称性，此次模拟采用与Li和Meng[5]相同的方式建立1/4模型，并在两个对称面上施加相应的对称边界条件.混凝土试件与SHPB杆之间的接触类型选用面面自动接触，算法采用LS-DYNA中被广泛应用的罚函数接触算法.在材料模型定义时，线弹性材料模型被用于模拟SHPB杆，而子弹则采用刚体材料模型进行模拟.其采用的网格尺寸径向是1 mm，纵向是2 mm.由于计算结果的收敛性主要受混凝土试件的网格尺寸影响，因此，分别采用1 mm、0.5 mm、0.25 mm和0.125 mm网格进行有限元试算.可以从计算结果中获取输入杆中点反射波的应力时程曲线，并将上述不同网格尺寸下试算的结果进行对比，如图2所示，由此分析模型计算结果的收敛性，试算时混凝土的应变率达到586 s-1.由图2可知，混凝土试件采用1 mm的网格和0.5 mm的网格时，其计算结果与0.25 mm的网格计算结果不能完全重合，但取0.125 mm网格与0.25 mm网格试算时，反射波的应力时程曲线几乎完全重合，这表明有限元计算结果已经收敛.因此，此次模拟对混凝土试件采用0.25 mm大小的网格进行划分.

图2 不同尺寸网格试算对比Fig.2 Comparison of the modeling results under different mesh sizes

名称长度l/m直径D/m弹性模量E/GPa密度ρkg/m泊松比v子弹0.20.0220078000.3输入杆10.0220078000.3透射杆10.0220078000.3试样0.0060.0122020000.2

本研究采用子弹的初速度控制入射应力波的峰值大小，不同的子弹速度将在SHPB试验装置中引起不同峰值大小的应力波，如图3所示.由图3可知，子弹的速度和入射应力波的大小近似成线性关系，其表达式为

σI=39.083×V

(8)

式中：σI为输入杆峰值应力，V为子弹速度.基于公式(8)，采用控制子弹速度的方法加载，在模型中对子弹初速度进行定义，实现对输入杆应力波和混凝土试件应变率大小的控制，这种方式比在输入杆的端部直接输入应力波的方法更为便捷.基于控制子弹速度的方法，进行不考虑端面摩擦效应的SHPB数值模拟，将模拟结果和文献[5]中给出的DIF与应变率的关系曲线进行对比，如图4所示.由于文献[5]也是基于不考虑端面摩擦效应得到的DIF应变率关系，由图4可知，模拟结果和已有DIF应变率关系曲线吻合程度较高，模拟结果在曲线附近波动变化.由此说明，采用子弹的初速度控制入射应力波的峰值大小的方法可靠，本研究将采用该方法实现应力波的输入.

图3 不同速度大小的应力波拟合Fig.3 Fitting different speed of stress wave

图4 模拟结果和试验结果对比Fig.4 Comparison of simulation results and test results

2.3 不同应变率下SHPB试验有限元模拟

本次SHPB试验的数值研究通过控制不同速度的子弹撞击输入杆，分析了在多种应变率下混凝土试块的动态抗压强度.为减少波的弥散效应本次模拟拟采用三角波[17]，通过模拟发现，在模型中当子弹采用刚体材料模型进行模拟时，得到的应力波呈三角波的形式.应变率为590 s-1时，计算的到的入射波、反射波和透射波，如图5所示，其中为了便于比较将透射波放大了10倍.可以根据公式(1)-(4)，计算得到多个应变率对应的重构的混凝土应力应变曲线，如图6所示，相应的应变率分别是：191 s-1、590 s-1和1 123 s-1.由图6可知，随着应变率的提高，混凝土的动态抗压强度增强，其强度按应变率从低到高依次为108 MPa、146 MPa和184 MPa，呈现出明显的增强效应，且随应变率的提高，混凝土应力应变曲线的损伤剧烈演化段的圆弧曲率减小，体现了高应变率下损伤演化的充分性.即随着应变率的提高，混凝土破坏更加充分，这与实际的混凝土SHPB试验力学行为本质非常相似，这一现象表明K&C模型适合表征混凝土在动荷载作用下的抗压力学性能.

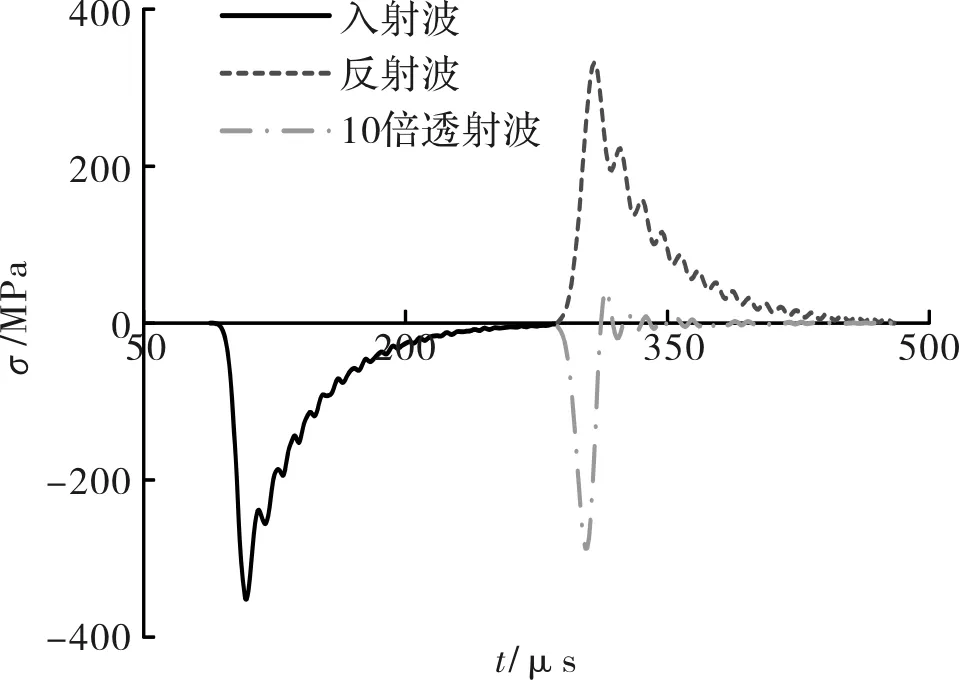
图5 模拟入射波、反射波和透射波Fig.5 Simulation waves of incident, reflection and transmission

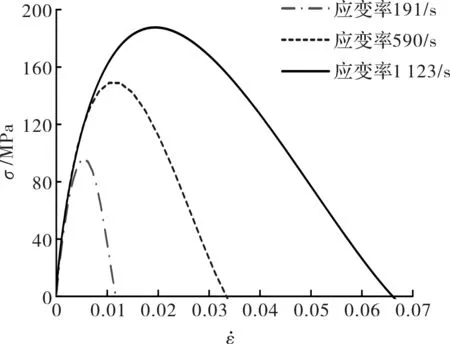
图6 不同应变率条件下重构应力应变曲线Fig.6 Reconstruction of stress-strain curves under different strain rate

3 考虑端面摩擦效应的SHPB模拟及结果讨论

针对端面摩擦效应，通过对混凝土与SHPB界面定义不同的μ(0，0.1，0.2，0.3和1.0)，实现了端面摩擦效应对DIF影响的量化分析，其有限元分析的计算结果如图7所示.由图7可知，μ的提高将引起对应的DIF增加.当应变率较低时，可以认为应变率低于102s-1时，DIF受μ的影响较小，但随着应变率的提高增强效应越显著，而应变率超过102s-1量级时，DIF增加幅度就几乎保持不变.当应变率高于102s-1时，与μ定义为0时的DIF值相比，当μ定义为0.1时DIF的增量为20%左右，当μ取0.2时，DIF的增量为35%左右，当μ定义为0.3时DIF增加了约45%.由图7和上述分析可知，随着μ的增加，DIF相对于μ取0时的增加幅度逐渐减小，体现为μ每增加0.1，DIF的增加幅度将会减小约5%.因此，随着μ的提高，DIF并不会一直增加，DIF受μ影响的增加量将存在上限，超过该上限值对应的μ值，DIF将受端面摩擦效应的影响较小.将混凝土界面μ设置为1时，其DIF较摩擦因数为0时增加了60%左右.因此可以证明端面摩擦效应对DIF的影响，即对混凝土动态抗压强度的最大提升效果约为无摩擦效应时的60%.

图7 模拟数据Fig.7 Simulated data

4 结论

(1)混凝土结构受动力荷载作用时，混凝土动态抗压强度相比准静态荷载作用下有明显的增强，而这种增强主要来源于结构效应，且端面摩擦效应对混凝土的动态抗压强度有着重要的影响.

(2)随着应变率的提高混凝土动态抗压强度也随之增加且混凝土损伤演化越充分，K&C局部损伤混凝土模型适合描述混凝土在动荷载作用下动态抗压的应力应变关系，能表征混凝土材料的损伤演化.

(3)DIF随着μ的增加而增加，但应变率较低时这种增强效应并不明显，当应变率达到102s-1量级时DIF的增加幅度几乎保持不变.随着μ的增加，DIF的增加幅度越来越小，当μ增加0.1，DIF的增加幅度将会降低5 %左右，最终端面摩擦效应对DIF的最大提升效果约为无摩擦效应时的60%.

[1] 李晓琴,陈建飞,陆勇,等.基于局部损伤混凝土模型的FRP-混凝土界面有限元分析研究[J].西安建筑科技大学学报(自然科学版),2015,47(1):62-65.

LI Xiaoqin, CHEN Jianfei, LU Yong, et al. Numerical analysis of FRP-concrete bond behavior based on a local concrete damage model[J]. J. of Xi′an Univ. of Arch. & Tech.(Natural Science Edition), 2015,47(1):62-65.

[2] BISCHOFF P H, PREEY S H. Compressive behaviour of concrete at high strain rates[J]. Materials and Structures, 1991, 24(6): 425-450.

[3] ZHANG M, WU H J, LI Q M, et al. Further investigation on the dynamic compressive strength enhancement of concrete like materials based on split Hopkinson pressure bar tests. Part I: Experiments[J]. International Journal of Impact Engineering, 2009, 36(12): 1327-1334.

[4] ROSSI P, VAN MIER J G M, TOUTLEMONDE F, et al. Effect of loading rate on the strength of concrete subjected to uniaxial tension[J]. Materials and Structures, 1994, 27(5): 260-264.

[5] LI Q M, MENG H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test[J]. International Journal of Solids and Structures, 2003, 40(2): 343-360.

[6] GEORGIN J F, REYNOUARD J M. Modeling of structures subjected to impact: concrete behaviour under high strain rate[J]. Cement and Concrete Composites, 2003, 25(1): 131-143.

[7] 翟毅,许金余,王鹏辉.纤维混凝土动态压缩力学性能的SHPB试验研究[J].西安建筑科技大学学报(自然科学版),2009,41(1):141-148.

ZHAI Yi, XU Jinyu, WANG Penghui. Dynamic compressive testing and mechanical behavior of fiber reinforced concrete using a split Hopkinson Pressure Bar[J]. J. of Xi′an Univ. of Arch. & Tech.(Natural Science Edition), 2009,41(1): 141-148.

[8] KIM D J, SIRIJAROONCHAI K, EL-TAWIL S, et al. Numerical simulation of the split Hopkinson pressure bar test technique for concrete under compression[J]. International Journal of Impact Engineering, 2010, 37(2): 141-149.

[9] LI Q M, LU Y B, MENG H. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part II: numerical simulations[J]. International Journal of Impact Engineering, 2009, 36(12): 1335-1345.

[10] KLEPACZKO J, MALINOWSKI Z. High velocity deformation of solids[C]. Berlin, Heidelberg : Springer, 1978: 403-416.

[11] BERTHOLF L D, KARNES C H. Two-dimensional analysis of the split Hopkinson pressure bar system[J]. Journal of the Mechanics and Physics of Solids, 1975, 23(1): 1-19.

[12] MU Z C, DANCYGIER A N, ZHANG W, et al. Revisiting the dynamic compressive behavior of concrete-like materials[J]. International Journal of Impact Engineering, 2012, 49: 91-102.

[13] MALVAR L J, CRAWFORD J E, WESEVICH J W, et al. A plasticity concrete material model for DYNA3D[J]. International Journal of Impact Engineering, 1997, 19(9): 847-873.

[14] Committee Euro-International du Beton. CEB-FIP Model Code[S]. Wiltshire, UK:Trowbridge, 1998.

[15] TU Z, LU Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations[J]. International Journal of Impact Engineering, 2009, 36(1): 132-146.

[16] 李晓琴, 陈保淇, 杜茜,等. 高应变率下混凝土材料的力学行为[J]. 云南大学学报:自然科学版,2016, 38(5):773-783.

[17] LI Xiaoqin, CHEN Baoqi, DU Xi, et al. The mechanic behaviour of concrete under high strain rates[J]. Journal of Yunnan University(Natural Science Edition), 2016, 38(5):773-783.

[18] 巫绪涛, 孙善飞, 李和平. 用HJC本构模型模拟混凝土SHPB 实验[J]. 爆炸与冲击, 2009, 29(2): 137-142.

WU Xutao, SUN Shanfei, LI Heping. Numerical simulation of SHPB tests for concrete by using HJC model[J]. Explosion and Shock Waves, 2009, 29(2): 137-142.