基于修正Peck法的隧道施工全地层变形规律研究
2018-05-29宋战平李世豪张学钢王军保
宋战平,李世豪,张学钢,3,王军保,王 涛
(1.西安建筑科技大学 土木工程学院,陕西 西安 710055;2.中国铁建大桥工程局集团有限公司,天津 300300;3.陕西铁路工程职业技术学院,陕西 渭南 714000)
地铁隧道暗挖施工不可避免的对围岩造成一定的扰动,地面将产生一定程度的沉降[1-4].如果土体的沉降位移变形过大,就会影响扰动范围内的建筑物基础和地下管线,并伴随着土体的不均匀沉降而发生变形,危害其正常安全使用.因此,研究隧道暗挖施工造成的全地层沉降位移进而评估其对邻近既有建(构)物的影响意义重大.
隧道和地下工程施工引起的地表沉降是城市地铁施工关注的重点,目前,预测地表沉降曲线的方法中,应用最广泛的属Peck法.Peck教授基于当时大量实测数据提出地表的沉降位移大致遵循正态分布的规律[2],Attewell[3]和Rankin[4]等人在此基础上总结出经典的Peck公式.另一种被广泛采用的方法是基于随机介质理论对地表沉降的计算.随机介质最初应用于采矿领域,经我国学者阳军生,刘宝琛等人[5-6]完善和拓展,引入到对隧道施工造成地表沉降研究.韩煊等人[7]对随机介质理论和Peck法进行了深入且全面的探讨,认为Peck法是随机介质理论在隧道深埋工况下的一个近似.随机介质较Peck法优势在于可以准确的计算浅埋隧道的地表沉降和水平位移,但是计算方法繁琐,在工程实践中难以广泛使用.Peck公式提出距今已接近半个世纪,但是其依然活跃在工程界里,不断有学者和工程师对其进行研究、修正[8-12],以适应更多地区土质的工况.隧道暗挖施工时地层的沉降主要与地层土的性质与厚度、隧道断面尺寸、隧道埋深及地层损失有直接关系.在利用Peck公式计算地层沉降时,已有文献[8-12]往往探究地层沉降槽的宽度与埋深的关系,忽略了各层地层土的性质与厚度和隧道开挖半径对沉降槽宽度造成的影响.Peck法最先是通过观测对地表的沉降研究[2-4],逐步转到地表下[8-12].而隧道暗挖施工最先扰动开挖面周边的土层,引起周边临近地层出现向隧道开挖空间的变形,造成隧道周边地层的损失;随着变形的发展,地层损失逐渐增加,在重力的作用下上覆地层逐渐变形,地层沉降由下向上逐渐发展,最终造成地表的沉降.因此,本文尝试从隧道暗挖施工造成拱顶上部土层的扰动出发,考虑各层地层土的性质与厚度和隧道半径对沉降槽的影响,探究各埋深地层的沉降规律,推导了Peck公式在不同埋深地层中的表达,得到了隧道上覆全地层土的修正Peck公式.基于修正的Peck公式,分别讨论了土层性质、厚度和隧道半径对地层沉降的影响.根据已有文献的实例对比分析验证了提出修正Peck公式的合理和可行性.
1 Peck法及其相关理论
R. B. Peck在大量实测数据的基础上提出地表沉降槽曲线大致服从正态分布的规律,用Peck公式表达,即:
(1)
式中:S(x)为地表任一点的沉降值;Smax为地表沉降的最大值,位于隧道中线对应的地表位置;x是地表距沉降中心线的水平距离;i被称为沉降槽宽度,是沉降槽中心线到曲线拐点(反弯点)的水平距离,如图1所示.
Peck提出地层损失的概念,他认为地层损失vl为隧道暗挖施工超挖部分的土体体积.在不排水不固结的情况下,地层损失体积等于地表沉降槽与原地表水平线围成的体积[2](图1),对Peck公式求积分得:
(2)
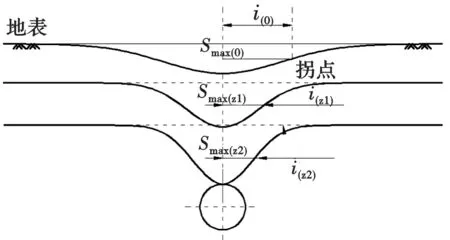
图1 地表沉降曲线(放大效果)Fig.1 The curve of the surface by tunneling(Amplified)
Mair等人[9]通过在黏土地区的实测资料,认为地表以下的土层沉降仍遵循正态分布的规律(即式(1)同样适用于地表以下土层),且沉降槽宽度随深度的增加会逐渐减小,如图1所示.即包括地表在内的任意地层的沉降满足下式:
(3)
由式(3)可知,在地层损失vl一定的情况下取得Smax(zi)或i(zi)中的任意一个表达式即可求得该土层沉降的Peck公式表达式.由于沉降槽宽度直观明显,尺寸较大,在进行实际测量时误差相对地层沉降小,因此,众多学者[8-12]多从沉降槽宽度入手研究地层的沉降规律.
2 沉降槽宽度求解
现有的沉降槽宽度计算方法多从沉降槽宽度与埋深关系出发[8-12],未考虑地层土的性质与厚度和隧道半径对沉降槽宽度造成的影响,所提出的公式只适用于某一类地质特性的土层.地层土的性质对沉降槽宽度有显著的影响,例如粘性土层和砂土层沉降槽宽度差异明显.且如果隧道拱顶到地表如有不同厚度和类别的土层,以上公式的适用性就存在很大局限.如果隧道开挖半径较大,那么受扰动的土体范围也较大,表现在沉降槽宽度上,沉降槽宽度变大.这也是韩煊等人对比了Peck法和随机介质理论得出Peck法适用于隧道断面小、埋深大的情况的原因[8].因此,单纯的寻求沉降槽宽度与埋深的关系的考虑是不够周到的,为此,本文寻求沉降槽宽度与各层地层土的性质和厚度、隧道半径以及地层埋深的关系.
本文尝试从隧道开挖面上土层的沉降位移规律出发,考虑各层地层土的性质、厚度和隧道半径,逐步向上推导,寻求各土层沉降规律表达式.
首先引入随机介质理论中地层影响半径r(z)的概念,r(z)为微单元开挖在埋深为z的水平面上的沉降主要影响半径,地表影响半径与隧道埋深z的关系式为[5-6]:
(4)
式中:β被称为主要影响角,为地表影响半径点与隧道埋深中心点的连线与地表水平线的夹角,如图2所示.对于地层影响角β的取值,S. Knothe[13]认为β=45°-φ/2,φ为土体的内摩擦角,众多学者也沿用此观点[14-15].地层土体的性质(内摩擦角φ)会影响地层影响角的取值.

图2 沉降槽宽度与地表影响半径关系(放大效果)Fig.2 Relationship between settlement trough and surface influence radius(Amplified)
韩煊等人[7]通过对比分析Peck法和随机介质理论得出地表影响半径和沉降槽宽度的关系:
(5)
对比式(2)和式(5)可知,r(z)的数学意义为地表沉降槽影响半径上的两点与沉降槽上沉降最大的点围成的三角形的面积等于沉降槽曲线与地表水平线围成的面积,即地层损失面积,如图2所示. 将地层影响角的概念引入到沉降槽宽度的表达式中,即将地层土体的性质对沉降槽宽度影响考虑在内.结合式(4)、(5)有
(6)
随机介质理论中提出的影响角被认为地表下某开挖单元完全塌落引起的地表下沉的基础上对地表的影响[5-6],而隧道开挖是在开挖完成后及时进行衬砌支护所引起的沉降是超挖部分的完全沉降.因此,笔者认为影响角是地表影响半径点与隧道衬砌某点的连线与地表水平线的夹角(如图3),而非地表影响半径点与隧道中心连线与地表水平线的夹角,众多学者也持此观点.

图3 第一层土层沉降示意Fig.3 The first layer of soil settlement
设埋深为z0+Smax(z0)+R,半径为R的隧道开挖造成vl的地层损失.隧道开挖地层损失部分土体由上层土层的沉降进行填补,如图3所示.则地层埋深为z0+Smax(z0)处的地层的地层影响半径可以近似按照下式计算
(7)
式中,β0为该地层的影响角.由于Smax(z0)与R相比非常小,工程计算中可以忽略不计,上式可以表达为
(8)
结合式(6)可求得
(9)
对式(6)求微分知
(10)
于是埋深为zi(0≤zi≤z0)处沉降槽的沉降槽宽度为
(11)
式中,地层影响角β因不同埋深的土层的土性不同而变化.
将式(9)带入式(11)有
(12)
根据式(12)可求得任意埋深土层的沉降槽宽度,由式(13)可求得该地层最大沉降值:
(13)
由此该地层的沉降槽表达式为
(14)
由式(14)可知,某一地层的沉降槽宽度主要与该地层下地层土的性质与厚度和地层隧道半径有关,即隧道半径和各地层土的性质和厚度影响沉降地层的沉降范围,而地层损失对沉降槽宽度影响不大,主要对沉降值的大小起作用.该推导也从理论上解释了文献[16]通过室内模型试验得出沉降槽宽度不会随沉降量增加而变化的原因.
3 工程实例验证与沉降槽宽度讨论
3.1 工程实例验证
选取工程地质资料较为详尽的文献[17]中的广州地铁赤岗-鹭江区段工程实测数据验证本文提出方法的合理性.该区段地铁隧道采用土压平衡盾构施工,刀盘直径为6.28 m,隧道外径6 m.隧道埋深为13.04 m,穿越复杂地层条件,岩土层的物理力学参数如表1所示.
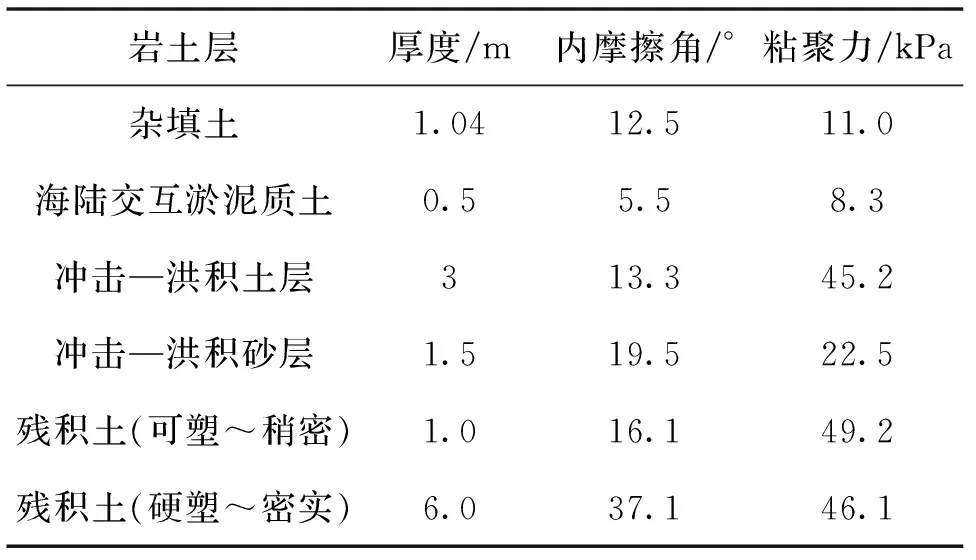
表1 岩土层物理力学参数
在对沉降槽宽度计算的过程中,各个土层的影响角取β=45°-φ/2.由于该监测数据中只有地表数据,因此取地表沉降验证.据式(12)计算地表沉降槽半径为9.64 m.取地层损失率为1.2%,则每延米的地层损失为vl=3.39×10-1m2.如此,根据式(13)计算出地表的最大沉降值为Smax=14.05 mm,进而推出地表沉降曲线表达式为
将计算出的地表沉降槽曲线与实测数据绘制于图4中.由图4可知实测数据排布在计算的沉降槽曲线两侧,在考虑工程测量误差等因素的前提下说明拟合度良好,证明了本文提出计算地层沉降曲线规律的合理性.

图4 计算结果与实测数据对比Fig.4 Comparison of calculated data with the measured data
3.2 土层性质和厚度及隧道半径对沉降槽宽度影响探讨
用本文提出的计算方法以工程实例验证部分中广州地铁赤岗-鹭江区段工程地质[17]为背景对土层性质和厚度及隧道半径对沉降槽宽度影响进行探讨.
设埋深10 m,外径6 m的隧道分别位于内摩擦角为5.5°的淤泥质土、内摩擦角为19.5°的冲击—洪积砂层和内摩擦角为37.1°的残积土中,在地层损失率为1.2%的情况下计算出地表沉降曲线,相关参数见表2所示,绘制地表沉降曲线如图5.
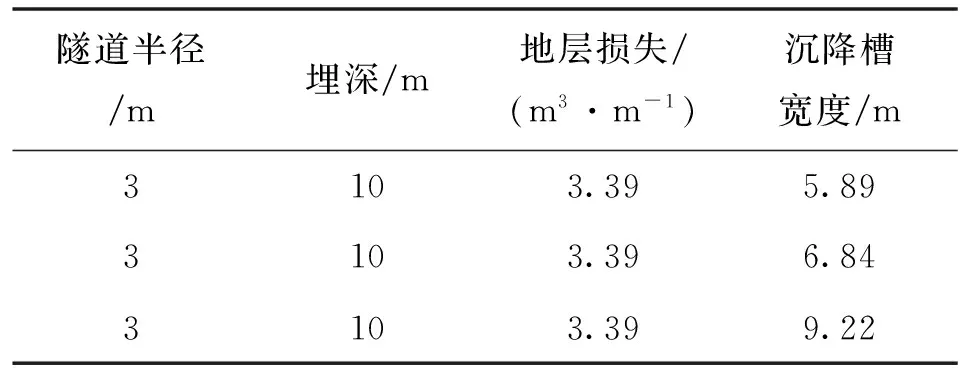
表2 土层性质对沉降槽宽度影响

图5 不同土层性质土层地表沉降曲线Fig.5 Surface settlement curves of different soil layers
由表2和图5可知,土层的内摩擦角越小,沉降槽越小,土层沉降曲线表现的越窄.沉降槽宽度随内摩擦角的增加而增大.
设埋深10 m,外径6 m的隧道位于内摩擦角为19.5°的冲击—洪积砂层中,在地层损失率为1.2%的情况下计算出地表、埋深3 m和埋深6 m的沉降曲线,相关参数见表3所示,绘制地表沉降曲线图于图6所示.

表3 土层埋深对沉降槽宽度影响

图6 不同埋深土层沉降曲线Fig.6 Settlement curves of different buried depths
由表3和图6可知,从地表向下,地层沉降曲线呈现越深越窄的变化趋势.地层埋深越大,沉降槽宽度越小,这与Mair等[10]的实验成果相一致.
设埋深10 m,外径分别为3 m、6 m、9 m的隧道位于内摩擦角为19.5°的冲击—洪积砂层中,在地层损失率为1.2%的情况下计算出地表的沉降曲线,相关参数见表4所示,绘制地表沉降曲线图如图7所示.

表4 隧道半径对沉降槽宽度影响

图7 不同隧道半径地表沉降曲线Fig.7 Surface settlement curves of different tunnel radius
由表4和图7可知,隧道半径对沉降槽宽度有微弱的影响,随着隧道半径的增大,沉降槽宽度有一定的增加.这是因为隧道半径越大,隧道暗挖施工对地层的扰动范围越大,进而对地层的沉降影响范围也越大.
4 结论
从隧道开挖对开挖面上部土体的扰动造成的沉降由隧道顶部逐步向上变形出发,考虑地层土性质、厚度和隧道半径对沉降槽宽度的影响,求得了隧道施工引起的沉降槽宽度在不同埋深的各土层的表达式,以分析隧道全地层的沉降变形规律,具有普遍适用性.基于修正Peck公式的研究和工程实例分析可得出以下结论:
(1)通过工程实测数据与本文提出的计算沉降曲线的方法所计算出的沉降曲线吻合效果良好,证明了本文提出沉降槽宽度计算方法的合理性.
(2)从理论上解释了沉降槽宽度不会随沉降量的增加而变化的原因.理论上地层损失的大小不会对沉降槽宽度造成影响.
(3)某一地层的沉降槽宽度主要取决于该地层与隧道开挖面之间的覆土性质和厚度,与隧道半径也有很大关系.覆土的内摩擦角越小,沉降槽的宽度越小,地层沉降曲线越窄.隧道半径越大,沉降槽宽度越大.
(4)在某一地区的隧道暗挖施工中,沉降影响的范围是确定的,减小地层的沉降量的核心在于控制地层损失.
[1] 宋战平, 张丹峰, 曲建生, 等. 承压富水砂土地层桩洞法施工变形控制研究[J]. 西安建筑科技大学学报(自然科学版), 2015, 47(1): 33-38.
SONG Zhanping, ZHANG Danfeng, QU Jiansheng, et al. Study on the deformation control of PBA construction method in pressure water sand stratum[J]. J. Xi′an Univ. of Arch.&Tech.(Natural Science Edition), 2015, 47(1): 33-38.
[2] PECK R B. Deep excavations and tunnelling in soft ground[A]// Proceedings of 7th international conference on soil Mechanics and foundation engineering. Mexico City: State of the Art Report, 1969. 225-290.
[3] ATTEWELL P B, YEATES J, SELLBY A R. Soil movements induced by tunnelling and their effects on pipelines and structures[M]. Glasgrow: Blackie,1986.
[4] RANKIN W J. Ground movement resulting from urban tunnelling: predictions and effects[J]. Geological Society,1988,5(1): 79-92.
[5] 阳军生, 刘宝琛. 挤压式盾构隧道施工引起的地表移动及变形[J]. 岩土力学, 1998,19(3): 10-13.
YANG Junsheng, LIU Baochen. Ground surface movement and deformation due to tunnel construction by squeezing shield[J]. Rock and Soil Mechanics, 1998, 19(3): 10-13.
[6] 阳军生, 刘宝琛. 城市隧道施工引起的地表移动及变形[M]. 北京:中国铁道出版社, 2002.
YANG Junsheng, LIU Baochen. Ground movement and deformation induced by urban tunnel construction [M]. Beijing: China Railway Publishing House,2002.
[7] 韩煊, 李宁. 隧道施工引起地层位移预测模型的对比分析[J]. 岩石力学与工程学报, 2007, 26(3): 594-599.
HAN Xuan, LI Ning. Comparative analysis of strata prediction models for ground movement induced by tunnel construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 594-599.
[8] O′ Reilly, M P, New B M. Settlements above tunnels in the United Kingdom—— their magnitude and predication[A]// Proceedings Tunnelling 82, London: Institution of Mining and Metallurgy London,1982.
[9] MAIR R J, TAYLOR R N, Bracgirdle A. Subsurface settlement profiles above tunnels in clay[J]. Geotechnique, 1993, 43(2): 315-320.
[10] STANDING J R, JARINE P M. Assessing the risk of building damage due to tunnelling-lessons from the Jubilee Line Extension, london[C]//Geotechnical Engineering: Meeting Society′s Needs: Proceedings of the Fourteenth Southeast Asian Geotechnical Conference. Hong Kong: CRC Press, 2001.
[11] 韩煊, 李宁, Standing J. R. 地铁隧道施工引起地层位移规律的探讨[J]. 岩土力学, 2007, 28(3): 609-613.
HAN Xuan, LI Ning, STANDING J. R.. Study on subsurface ground movement caused by urban tunnelling[J]. Rook and Soil Mechnics 2007, 28(3): 609-613.
[12] 姜忻良, 赵志民, 李园. 隧道开挖引起土层沉降槽曲线形态的分析与计算[J]. 岩土力学, 2004, 25(10): 1542-1544.
JIANG Xinliang, ZHAO Zhimin, Li Yuan. Analysis and calculation of surface and subsurface settlement trough profiles due to tunneling[J]. Rock and Soil Mechanics, 2004, 25(10): 1542-1544.
[13] KNOTHE S. Observations of surface movements under influence of mining and their theoretical interpretation[C]// Proceedings of European Conference on Ground Movement. Leeds, UK: University of Leeds, 1957: 210-218.
[14] 刘建航, 候学渊. 盾构法隧道[M]. 北京:中国铁道出版社, 1991.
LIU Jianhang, HOU Xueyuan. Shield tunnel[M]. Beijing: China Railway Publishing House, 1991.
[15] 王建秀, 田普卓, 付慧仙, 等. 基于地层损失的盾构隧道地面沉降控制[J]. 地下空间与工程学报, 2012, 8(3): 569-576.
WANG Jianxiu, TIAN Puzhuo, FU Huixian, et al. Ground settlement controlling of shield tunnel by strata loss theory[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(3): 569-576.
[16] 臧宏阳, 王非. 盾构隧道施工时地层沉降模型试验研究[J]. 地下空间与工程学报, 2015, 11(3): 568-572.
ZANG Hongyang, WANG Fei. Large-scale physical modelling on the ground settlement induced by shield tunneling[J]. Chinese Journal of Underground Space and Engineering,2015, 11(3): 568-572.
[17] 刘波, 陶龙光, 李希平, 等. 地铁盾构隧道下穿建筑基础诱发地层变形研究[J]. 地下空间与工程学报, 2006, 2(4): 621-626.
LIU Bo, TAO Longguang, LI Xiping, et al. Research of ground settlement induced by metro shield tunnel beneath building foundations[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(4): 621-626.
