扣件不同紧固力矩对工字钢悬挑钢管外脚手架变形影响分析

何夕平，王 璜，赵雪会

(安徽建筑大学 土木工程学院，安徽 合肥 230601)

在房建工程施工安全事故中，脚手架坍塌事故占了很大的比例，其中，由于脚手架架体变形过大导致的事故比比皆是，往往造成重大生命财产损失和不良的社会影响.

工字钢悬挑钢管外脚手架是一种常用于高层建筑施工的外脚手架.纵观已发生的脚手架事故，人为因素是首要的原因[1]，其中：忽视脚手架安全施工方案、扣件紧固力矩值严重不足、脚手架施工荷载超载和施工现场管理混乱等，而由于扣件紧固力矩值不足导致脚手架变形过大，导致脚手架事故不胜枚举.由于市场上的钢管、扣件等材料质量参差不齐，使得工字钢悬挑钢管外脚手架在实际使用时产生地变形不能满足现行国家规范的要求.通过查阅国内外相关文献，关于脚手架的理论分析研究和试验研究，把架体看做铰接结构体系、半刚性结构体系和刚性结构体系，采用规范推荐法、弹性屈曲分析法和非线性有限元分析等方法，对架体的受力传递规律、变形特征、整体稳定性等有全面系统的分析，但对扣件紧固力矩对脚手架的影响研究相对较少，鉴于工字钢悬挑钢管外脚手架悬挑出建筑物主体结构这种搭载方式，具有很大的危险性，因此，有必要对扣件式钢管外脚手架采用工字钢悬挑搭设方式的变形进行分析研究.

首先进行直角扣件抗扭转试验，在此试验结果基础上，利用有限元结构分析软件SAP2000建立工字钢悬挑扣件式钢管外脚手架实体模型，分析扣件不同紧固力矩值对工字钢悬挑外脚手架变形的影响[2-3].

1 直角扣件抗扭转试验

工字钢悬挑钢管外脚手架采用直角扣件连接，连接节点刚性处于纯铰接和理想刚接之间，刚性大小主要由施加在扣件螺栓上的紧固力矩值大小决定[4].

在室内开展直角扣件抗扭转试验，来确定直角扣件竖直平面内的抗扭转刚性.同时为模拟施工现场脚手架上扣件真实受力状态，用于试验的扣件、钢管均随机选自工程现场.由于现场使用的钢管多次周转和部分锈蚀等因素，经量测钢管外直径为φ48.3 mm，壁厚为3.0 mm.

本次抗扭转试验共选择20个直角扣件，分为5组进行.由于直角扣件刚性受扣件紧固力矩值影响，试验分五组紧固力矩值等级，用数显力矩扳手拧紧螺栓至对应等级，各组等级分别设置为30 N·m、35 N·m、40 N·m、45 N·m和50 N·m.直角扣件在扭转力矩作用下，竖直杆的扭转变形通过设置在距离直角扣件中心上方L1=200 mm处的位移计1和中心右侧L2=200 mm处位移计2测得.集中荷载加载装置为万能试验机和液压千斤顶，在水平杆距离直角扣件中心水平间距L3=500 mm的加载点上分级加载，每级加载0.1 kN，直至扣件破坏，破坏标准为连续加载3级，位移计指针无变化.试验装置和示意图见图1-图2.

图1 试验装置图Fig.1 Diagram of experimental device

图2 试验装置示意图Fig.2 Schematic diagram of experimental Device

由图2和文献[5]可知扣件的转角位移：

(1)

式中：θ为直角扣件的转角位移；Δ1为位移计1测得的位移；Δ2为位移计2测得的位移；L1为直角扣件中心至位移计1的竖向距离；L2为直角扣件中心至位移计2的水平距离.

将每组试验数据的平均值代入公式(1)，求得转角位移θ，并绘制出在不同紧固力矩值下直角扣件扭转弯矩与转角的关系曲线(M-θ曲线)，如图3所示.

图3 不同紧固力矩值时直角扣件弯矩—转角关系曲线Fig.3 Moment and rotation angle curve of right angle coupler under different tightening torques

从图3中可看出，不同紧固力矩值下直角扣件扭转弯矩与转角呈非线性关系，扣件紧固力矩值对扣件抗扭转刚度有直接影响.同时，在相同弯矩值下，紧固力矩值与扣件抗扭转刚度成正比，与转角变形成反比.

由图3可知，扣件在紧固力矩30～50 N·m范围内，破坏弯矩在0.9 ～1.1 kN·m之间，相差不大.结合文献[6]，以扣件发生材料破坏的前提，取0.9 kN·m作为经多次周转、存在一定磨损和锈蚀的旧直角扣件的极限弯矩承载力是较合适的.

2 M-θ曲线的数学模型

由上述抗扭转实验数据，结合图3的图形特征，使用MATLAB数学软件拟合，得到直角扣件弯矩—转角关系曲线M-θ的三次多项式数学模型[4-6]，三次多项式数学模型见表1.

根据M-θ曲线的特点，同时也便于SAP2000模拟分析，提出以分段折线模型代替M-θ曲线模型[6, 8]，并得到不同紧固力矩下扣件线刚度系数，见表2.

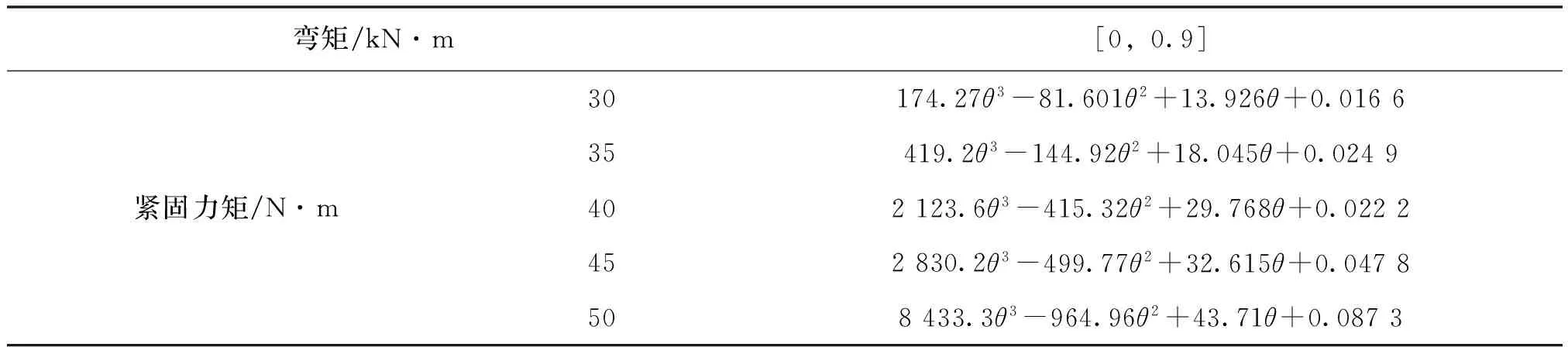
表1 不同紧固力矩时直角扣件弯矩—转角(M-θ)曲线三次多项式模型

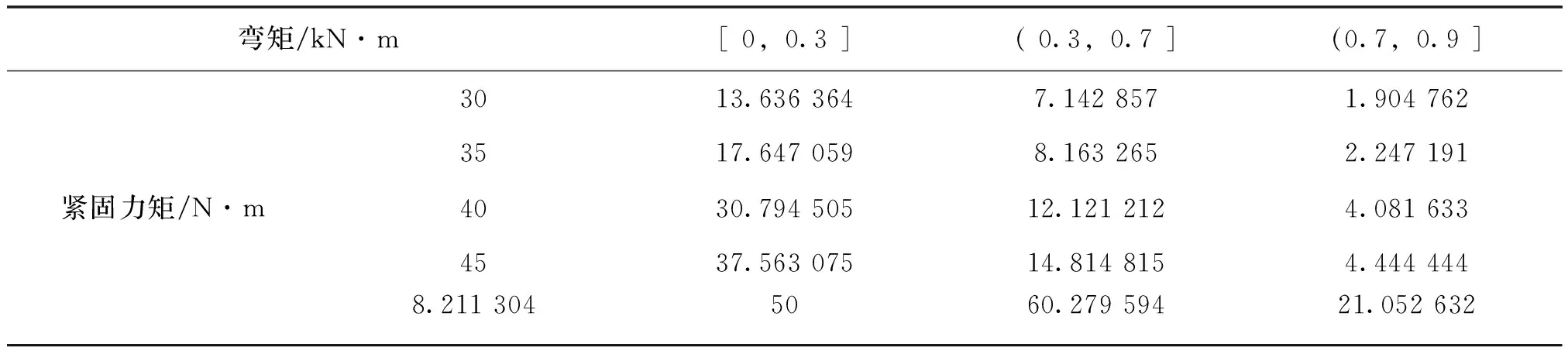
表2 不同紧固力矩直角扣件线刚度系数(kN·m/rad)

3 工字钢悬挑扣件式钢管外脚手架实体模型的建立

3.1 工字钢悬挑扣件式钢管外脚手架实体模型的简化处理

竹笆脚手板和木脚手板挡板等构配件自重等效成均布线荷载作用在相应的水平杆上；施工均布荷载按2.5 kN/m2计算，以考虑架体上有2个作业层同时工作；作用在悬挑架上的风荷载等效成线荷载作用在立杆上[9-10].

实际工程中，工字钢悬挑钢管外脚手架不可避免存在一定的初始缺陷，如钢管的初始挠度、 锈蚀、断面不平整，以及架体中纵横向水平杆和立杆不垂直等，这些初始缺陷都直接影响悬挑架的变形[11-12].在SAP2000有限元分析中，通过在架体横向水平杆和立杆连接节点作用大小为1 kN的虚拟集中荷载来作为考虑这些初始缺陷对架体变形的影响，该集中荷载平行于架体刚性较弱一侧[13-17].本文模型分析忽略了地震和其他水平荷载的影响.

3.2 工字钢悬挑扣件式钢管外脚手架实体模型的建立

某工程外脚手架采用主次梁工字钢悬挑扣件式钢管，搭设高度为19.2 m，搭设参数如下：

步距18 m；立杆纵距为1.5 m；立杆横距为1.05 m；悬挑型钢主梁为18#热轧2号钢；型钢次梁为14#热轧工字钢；剪刀撑为5步5跨；连墙件为2步2跨.

在有限元模型中，采用框架-钢截面-圆管单元模拟钢管，框架-钢截面-工字钢单元模拟型钢，铸铁扣件采用2节点连接模拟，限制2节点连接两端的x、y、z三个轴向平动位移和转角.选用多段线弹性单元(Multi-Linear Elastic)作为2节点连接类型，U1、U2、U3、R2、R3方向属性均选为固定，R1选为非线性，并按表3输入M-θ数据.将立杆底端设置为弯矩释放，保证立杆与工字钢悬挑主梁的连接为铰接.为研究工字钢悬挑扣件式钢管外脚手架变形和直角扣件紧固力矩值之间的关系，有限元模型分为5种不同工况研究分析，分别为工况1～工况5，直角扣件紧固力矩值变化分为五个等级，分别为30 N·m、35 N·m、40 N·m、45 N·m和50 N·m，其他搭设根据国家现行相关规范要求执行.

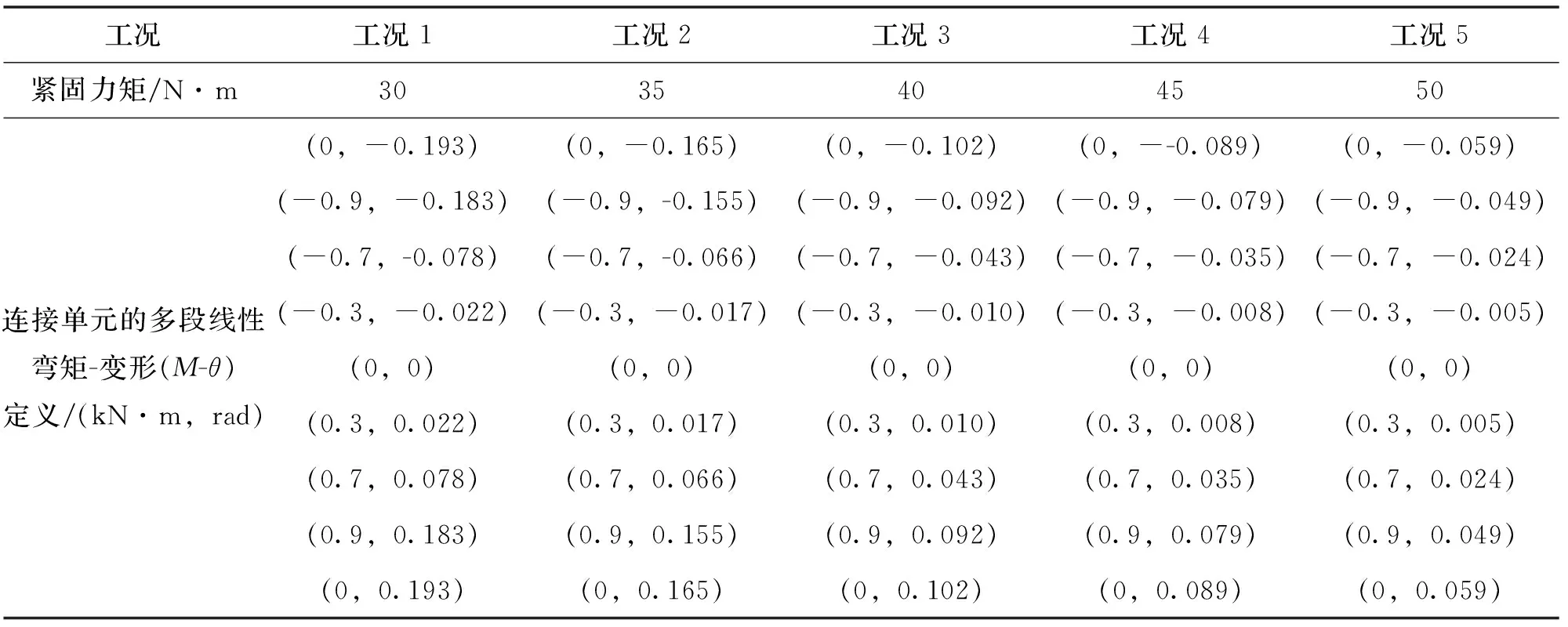
表3 不同紧固力矩值时连接单元的多段线性弯矩-转角(M-θ)定义

按照上述参数和处理方式建立工字钢悬挑扣件式钢管外脚手架模型，如图4所示.

图4 工字钢悬挑钢管外脚手架有限元模型Fig.4 Finite element model of I-steel cantilever external scaffold

4 对扣件不同紧固力矩值悬挑架有限元分析

运用SAP2000对工况1—工况5的悬挑架模型进行有限元非线性分析.得到该工程在工况1-工况5下的常规部位和转角处18#悬挑工字钢主梁、14#工字钢次梁、纵向水平杆、横向水平杆的最大挠度变形和18#悬挑工字钢主梁承受的集中力，分别如表4—表5所示.18#悬挑工字钢主梁挠度变形在悬挑远端节点处最大，常规部位最大值为节点位移U3，如图5所示.

图5 工况3常规部位18#工字钢最大挠度变形值Fig.5 Largest definition of No.18 I-steel at conventional site in No.3 condition

工况工况1工况2工况3工况4工况5容许挠度常规部位18#工字钢主梁10.06589.85469.35489.12808.651811.6纵向水平杆0.18690.18580.18530.16170.161610横向水平杆2.03271.97541.82991.75991.60227转角处18#工字钢主梁9.59259.38958.91328.69848.235216.402414#工字钢次梁4.04153.83733.39363.32092.856310纵向水平杆0.94600.92610.87930.85970.819910横向水平杆3.95383.70383.14872.91282.65377

注：水平杆和工字钢容许挠度根据国家现行规范计算取值.单位：mm.

表5 18#工字钢承受的集中力

注：表中F1、F2分别表示脚手架内、外侧立杆传递至18#工字钢的集中力.单位：N.

根据数值模拟分析知，相同荷载作用下，扣件紧固力矩值与纵向水平杆的支座反力和负弯矩成正比，与正弯矩和挠度成反比，与横向水平杆挠度成反比.通过分析表5，发现扣件紧固力矩值与脚手架内侧立杆传递至工字钢主梁上的集中力F2成正比，与外侧立杆传递至工字钢主梁上的集中力F1成反比.所以，18#工字钢主梁最大挠度随着工况1-工况5扣件紧固力矩值的增大而减小.18#工字钢主梁承受的集中力如图6所示.

与工况1相比，随着工况1-工况5紧固力矩值每增大5 N·m，悬挑架工字钢主梁、工字钢次梁、纵向水平杆、横向水平杆最大挠度变形下降幅度如表7所示.

图6 18#工字钢承受的集中力示意图Fig.6 Schematic diagram of concentrated forces on 18# I-steel

工况工况2工况3工况4工况5常规部位18#工字钢主梁2.1%7.0%9.3%14.0%纵向水平杆0.6%1.8%13.5%13.6%横向水平杆2.8%10.0%13.4%21.2%转角处18#工字钢主梁2.1%7.1%9.3%14.1%14#工字钢次梁5.1%16.0%17.8%29.3%纵向水平杆2.1%7.1%9.1%13.3%横向水平杆6.3%20.4%26.3%32.9%

注：表中各工况数据均是相对于工况1各构件挠度变形下降幅度

分析表6知，随着由工况1至工况5扣件紧固力矩值的增加，工字钢悬挑扣件式钢管外脚手架中工字钢、纵、横水平杆等构件的挠度呈下降趋势，且下降幅度明显.工况5相对于工况1常规部位工字钢主梁、纵、横向水平杆最大挠度下降幅度分别达到14.0%，13.6%和21.2%；转角处工字钢主梁、工字钢次梁、纵、横向水平杆最大挠度下降幅度分别达到14.1%、29.3%、13.3%和32.9 %.在常规部位，最大挠度变形18#工字钢悬挑主梁减小值最大，减小值1.504 mm.在扭转试验中，部分质量不好的直角扣件，紧固力矩值还未达到规范要求的45 N·m时就出现滑丝破坏现象，从而失去了扣件应有的约束作用，所以，在实际工程中，对于锈蚀的扣件应避免出现扭矩过大.考虑到施工现场钢管的多次周转使用、初始弯曲、锈蚀等不利因素，在满足规范中要求允许变形的条件下，还应留有一定的安全储备，因此，建议对已多次使用锈蚀的扣件紧固力矩值设置为40 N·m较为合理.

5 结论

(1) 通过对比分析抗扭转试验数据，当紧固力矩值设置为30 N·m、35 N·m、40 N·m、45 N·m和50 N·m时，可以得出扣件相对转角位移受螺栓紧固力矩值数值影响.在相同弯矩作用下，随着螺栓紧固力矩值增大，扣件相对转角位移将减小.

(2) 施工现场经多次周转使用的直角扣件，取0.9 kN·m作为极限弯矩承载力较合适.

(3)对于工字钢悬挑钢管外脚手架，增大直角扣件紧固力矩值可有效的减小各个构件最大挠度变形值，其中工字钢悬挑主梁最大挠度减小尤为明显.通过本文实际工程架体搭设情况分析，对已多次使用锈蚀的旧直角扣件取紧固力矩值为40 N·m较为合理，同时本文的分析方法和结论可供悬挑脚手架工程借鉴.

[1] 陆征然，陈志华，王小盾，等.扣件式钢管满堂支撑体系稳定性的有限元分析及试验研究[J]. 土木工程学报，2012，45(1)；49-60.

LU Zhengran, CHEN Zhihua，WANG Xiaodun, et al. Experimental and theoretical study of the bearing capacity of fastener steel tube full-hall formwork support system[J]. China Civil Engineering Journal, 2012, 45(1):49-60.

[2] TURKER T, KARTAL M E, BAYRAKTAR A, et al. Assessment of semi-rigid connections in steel structures by modal testing[J]. Journal of Construction Research . 2009,65(7)：1538-1547.

[3] 王璜,工字钢悬挑钢管外脚手架受力机理和安全性分析研究[D].合肥：安徽建筑大学，2016.

WANG Huang. Analysis of force mechanism and safety of I-steel cantilever external scaffold[D]. Hefei： Anhui Jianzhu University，2016.

[4] 袁雪霞，金伟良，鲁征，等.扣件式钢管支模架稳定承载能力研究[J].土木工程学报，2006，39(5)：43-50.

YUAN Xuexia, JIN Weiliang, LU Zheng, et al. A study on the stability bearing capacity of fastener-style tubular steel formwork-supports[J]. China Civil Engineering Journal, 2006， 39(5)：43-50.

[5] 陈志华，陆征然，王小盾.钢管脚手架直角扣件刚度的数值模拟分析及试验研究[J].土木工程学报，2010， 43(9)：100-108.

CHEN Zhihua, LU Zhengran, WANG XIaodun. Numerical analysis and experimental study of the stiffness of right angle couplers in tubular steel scaffolds[J]. China Civil Engineering Journal, 2010， 43(9)：100-108.

[6] 朱启新，万雨辰，张其林.钢管脚手架扣件节点的转动刚度试验和计算模型[J].山东建筑大学学报，2010，25(5)：499-502，518.

ZHU Qixin, WAN Yuchen, ZHANG Qilin. Rotational stiffness test and calculation model of steel scaffolds′ coupler connections[J]. Journal of Shandong Jianzhu University. 2010，25(5)：499-502,518.

[7] 刘红波，赵秋红，王小盾，等.无剪刀撑结构钢管和扣件脚手架稳定性试验分析研究[J].工程结构.2010，32(4)：1003-1015.

LIU Hongbo, ZHAO Qiuhong, WANG Xiaodun, et al. Experimental and analytical studies on the stability of structural steel tube and coupler scaffolds without X-bracing[J].Engineering Structures, 2010,32 (4)：1003-1015.

[8] 北京金土木软件公司，中国建筑标准设计研究院. SAP2000中文版使用指南 [M]. (第二版).北京：人民交通出版社，2012.55-58.

Beijing Golden Civil Software Company, China institute of building standard design & research. guide for use in Chinese of SAP2000 [M].2nd ed. Beijing: People Communications Press, 2012.55-58.

[9] 中华人民共和国住房和城乡建设部.建筑施工扣件式钢管脚手架安全技术规范:GJ 130-2011[S]. 北京：中国建筑工业出版社，2011.

Ministry of Housing and Urban-rural Development of the People′s Republic of China. Technical code for safety of steel tubular scaffold with couplers in construction: JGJ 130-2011 [S]. Beijing：China Architecture & Building Press，2011.

[10] 中华人民共和国住房和城乡建设部. 建筑施工临时支撑结构技术规范:JGJ 300-2013[S].北京：中国建筑工业出版社，2013.

Ministry of Housing and Urban-rural Development of the People′s Republic of China. Technical code for temporary support structures in construction: JGJ 300-2013[S]. Beijing： China Architecture & Building Press，2013.

[11] 胡长明.扣件联接钢结构的试验及其理论研究[D].西安：西安建筑科技大学，2008.

HU Changming. Studies on experimental and theory of steel construction connected with fasteners[D]. Xi′an：Xi′an Univ. of Arch. & Tech., 2008.

[12] 范小周.扣件式钢管高大模板支撑体系广义初始缺陷及性能分析[D].西安：西安建筑科技大学，2012.

FAN Xiaozhou. Analysis of generalized initial imperfection and performance test of fastener steel style high-false work support system[D].Xi′an ：Xi′an Univ. of Arch. & Tech.. 2012.

[13] 胡长明，曾凡奎，王静，等.广义初始缺陷对模板支架稳定性的影响[J].工业建筑，2010，40(2)：17-19，27.

HU Changming, ZENG Fankui, WANG Jing, et al. Influence of generalized initial imperfections on steel construction connected with fasteners[J]. Industrial Construction，2010，40(2)：17-19, 27.

[14] 周璇，曾志兴.双排扣件式钢管脚手架横向斜撑结构的优化[J].工业建筑，2011,41(1)：23-25.

ZHOU Xuan, ZENG Zhixing. Structural optimization on lateral bracing of tubular steel scaffold joining by couplers[J]. Industrial Construction，2011,41(1)：23-25.

[15] 何夕平，齐华伟，邵传林.满堂扣件式钢管脚手架不同步距承载力影响分析[J].安徽建筑大学学报，2015，23(4)：11-16.

HE Xiping, QI Huawei, SHAO chuanlin. Bearing capacity influence analysis of different lift height of fastener steel tube full hall scaffold[J]. Journal of Anhui Jianzhu University, 2015,23(4)：11-16.

[16] 胡长明，车佳玲，张化振，等.节点半刚性对扣件式钢管支模架稳定承载力的影响分析[J].工业建筑，2010，40(2):20-23.

HU Changming, CHE jialing, ZHANG Huazhen, et al. Influence of semi-rigid joint on stability capacity of coupler steel tube false work[J]. Industrial Construction，2010，40(2)：20-23.

[17] 周洪涛，郭志鑫.扣件式钢管满堂脚手架ANSYS受力性能分析[J].施工技术，2013,42(14)：98-101.

ZHOU HOngtao, ZUO Zhixin. Mechanical analysis of fastener steel tube full hall scaffold with ANSYS[J]. Construction technology，2013,42(14)：98-101.