双变量耦合作用对非饱和岩土波动特性的影响研究

胡亚元

( 浙江大学 滨海和城市岩土工程研究中心，杭州 310027)

岩土介质中波的传播特性及动力响应研究一直受到理论力学界和工程界的重视。它不仅对弹性动力学发展具有重要理论价值，而且在地震学、地球物理学、石油工程、土木工程、动力机器基础和防护工程等工程领域具有广阔应用前景。近年来，随着非饱和岩土力学的发展，对波在非饱和岩土的传播特性和动力响应的研究越来越深入，但采用双变量理论(双应力或双应变)研究非饱和岩土波动特性的文献目前还极其少见，因此有必要开展双变量理论框架下的非饱和岩土波动特性研究。

建立非饱和岩土波动理论控制方程的方法主要有两种。一种是Biot创建的工程法[1-2]。Brutsaert[3]和Santos等[4]把非饱和岩土看成由固液气三相连续组成的多孔介质，基于Lagrangian坐标系把Biot饱和岩土波动理论扩展到非饱和岩土波动理论，理论证明在非饱和岩土中除与饱和岩土对应的剪切波S波、快纵波P1波和第一慢纵波P2波外，还存在与第二种流体对应的第二慢纵波P3波。 蔡袁强等[5]和徐明江[6]从单变量理论出发，应用Skempton有效应力公式[7]，建立了非饱和岩土波动方程并深入研究非饱和岩土四种体波(包括三个纵波和一个横波)的传播特性。另一种是混合物理论法。Vardoulakis等[8]采用混合物理论建立了非饱和岩土波动方程，徐长节等[9]采用Vardoulakis波动方程深入研究了非饱和土中三种弹性纵波的波动特性。Wei等[10-11]根据相分离原理建立了非饱和岩土波动控制方程，黄义和张引科[12]在忽略固相和液相材料变形的条件下根据混合物理论建立了非饱和土的波动控制方程，系统建立了求解非饱和土动力响应的边界元理论。Chen等[13]根据Wei等建立的非饱和岩土波动方程，忽略流体组分体积分数对流体自由能影响，深入分析了非饱和岩土的表面波传播特性。上述这些研究深化了工程界对弹性波在非饱和岩土介质中传播特性的认识，极大地推动了非饱和岩土波动理论的发展。但由于非饱和土中固液气三相相互作用的复杂性，对非饱和岩土波动控制方程的研究仍然存在一些不足，主要表现在两个方面:①某些非饱和岩土波动方程中的模型参数取值比较困难，比如徐明江指出，按照混合物理论建立的一些非饱和岩土波动方程存在这类困难。②Fredlund理论[14]表明，非饱和岩土的力学特性需要采用双变量才能得到合理地反映,因此非饱和岩土的波动方程也需要依据双变量理论来建立。然而目前采用双变量理论来研究非饱和岩土波动特性和动力响应的文献还很少见，亟需填补这方面的研究空缺。

本文从Houlsby等[15]，Borja[16]和胡亚元[17]创建的非饱和多孔介质工程力学理论出发，根据能量平衡方程和热力学局部平衡原理构建自由能势函数，在假定各组分材料之间以及它们与骨架之间的力学特性均不相互耦合的前提下建立了以双变量理论为基础的非饱和岩土弹性本构方程。根据不同双变量建立的线弹性本构方程相互一致的性质，推导出弹性本构方程模型参数与非饱和岩土常规土工参数之间的换算公式。利用非平衡态热力学熵产公式构建渗流耗散率势函数，获得液气两相的达西渗流本构方程。把上述本构方程与动量守恒方程相结合，获得一个以双应力变量为基础的非饱和岩土线弹性波动控制方程。最后，通过算例分析了双应力变量耦合效应对非饱和土三个纵波和一个横波波速的影响规律。

1 波动方程

1.1 动量和动量矩守恒

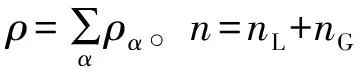
Sr=nL/(nL+nG)

(1)

根据各组分体积分数的定义，有：

nS+nL+nG=nS+n=1

(2)

(3)

设σα为第α组分的柯西应力，σ为混合物总柯西应力，根据混合物理论有：

(4)

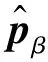
(5a)

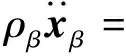
(5b)

不考虑力偶供应量，根据各相的角动量守恒方程可得各相的柯西应力张量是对称张量。

1.2 能量平衡方程

(6)

定义Bishop 平均有效应力为[15-16，19-20]：

(7)

(8)

(9)

令Pr=-σ∶1/3为多孔介质的总压力，则定义固相的真实压力为：

(10)

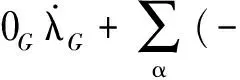
(11)

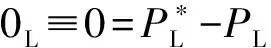
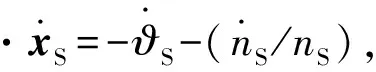
(12)

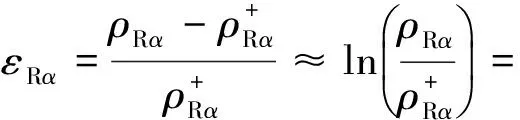
(13)

设εS为ES在小应变条件下的固相应变张量，则根据ES和EH的关系有：

(14a)

根据组分体应变与其密度之间存在的数学关系[21],由ρL=SrnρRL，ρG=(1-Sr)nρRG并利用式(12)可得小应变条件下液气两相的组分体应变εLv和εGv分别为:

(14b)

(14c)

(15)

根据大应变和小应变之间物理量的关系，由式(11)～(13)和式(15)可得：

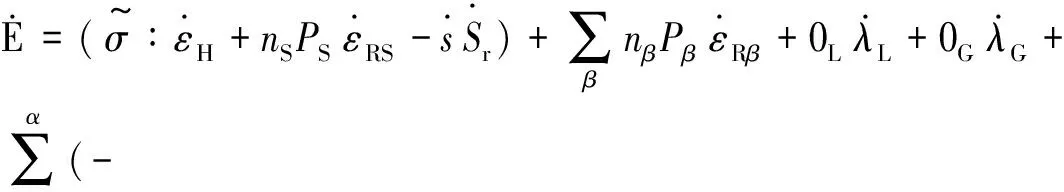
(16)

式(16)即是小应变条件下非饱和多孔介质混合物的能量平衡方程。

1.3 线弹性方程和线性渗流方程

根据能量平衡方程，等存性公设和Lagrangian乘子法理论，弹性条件下非饱和多孔介质的自由能可假定为：

E(η,εH,Sr,εRα,λL,λG)=

(17)

对式(17)进行微分得：

(18)

根据热力学局部平衡假定，可得：

(19a)

(19b)

引入Helmhotlz自由能Ψ*(θ,εH，Sr，εRα)，它与内能之间的关系为：

Ψ*(θ,εH，Sr,εRα)=E*(η,εH,Sr,εRα)-θη

(20)

把式(20)两边微分再把式(19a)代入得：

(21)

(22)

式中：DHH、KRαγ、Krr、Kθθ、KRHα、KHr、KHθ、KRrα、KRθα、Kθr是模型弹性系数，KRαγ=KRγα，α∈{S,L,G}，γ∈{S,L,G}。把式(22)代入到式(21)得：

(23a)

(23b)

(23c)

(23d)

在目前通行的饱和和非饱和岩土力学中，均假定各组分材料的本构模型在形式上与其单相时的本构模型相同[14,20]，即其压力只与其本身的体积变形和温度有关而与其它相的变形无关。在该假定下，各组分的材料变形之间以及它们与骨架变形之间均相互解耦。同时假定波动过程处于热力学等温过程，故取θΔ=0。利用这些假定，式(23a)～(23d)简化为：

(24a)

(24b)

nαPα=KRααεRαα∈{S,L,G}

(24c)

式(24a)～(24b)表明，当Bishop平均应力需要采用双应变变量表达时，修正吸力也要采用双应变变量来表示。如果修正吸力不相应地采用双应变变量来表示，则由此获得的波动方程刚度矩阵就会失去对称性。同时，由于土工试验表明岩土和混凝土等非饱和多孔介质的基本力学性质及其本构关系需要采用双变量(双应变或双应力)来表示，因此式(24a)～(24c)是其最简单形式。从式(20)～(24c)的推导过程看，与文献[12]相比，本文不但考虑了固相和液相自身的材料变形，而且还大大减少了模型参数，简化了获得非饱和岩土线弹性本构关系的推导过程。与蔡袁强等基于工程法提出的非饱和岩土单变量线弹性本构模型相比，本文式(24a)～(24b)考虑了骨架变形和饱和度之间的耦合作用，它不仅与当前非饱和岩土力学的双变量理论之间更加一致，而且因为修正吸力也采用了双应变变量来表示，所以满足弹性功互易定理，线弹性本构方程的刚度矩阵相应地也成为对称矩阵。

当固相骨架为各向同性材料时，式(24a)～(24b)简化为：

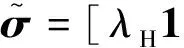
(25a)

(25b)

式中：λH和G为骨架Lame常数；KHr为骨架和毛细吸附作用之间的耦合刚度；Krr为修正吸力关于饱和度的刚度；1为二阶单位张量；14为四阶单位张量，(14)ijkl=(δikδjl+δilδjk)/2。对式(25a)～(25b)以及式(24c)求逆得：

(26a)

(26b)

(26c)

式中：EH为骨架的杨氏模量；υ有骨架的泊松比；EHr为骨架和毛细吸附耦合作用之间的弹性模量；Err为饱和度随吸力变化的弹性模量。由于式(25a)～(25b)和式(26a)～(26b)互逆，固有：

(27a)

(27b)

(27c)

(28a)

(28b)

(28c)

把式(28a)～(28c)代入到式(26c)得：

(29a)

(29b)

把式(26a)，式(28a)～(28c)和式(29a)代入式(14a)得：

(30)

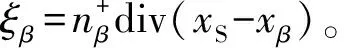
(31a)

(31b)

把式(26a)～(26c)、式(28a)～(28c)和式(29a)～(29b)代入式(31a) ～(31b)得：

(32a)

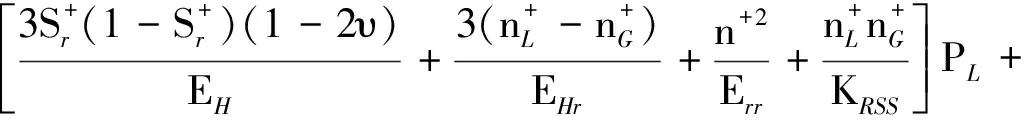
(32b)

由于在波动理论中不考虑热流量和外热供应，故qα=0，rα=0。把式(18)代入到式(16)并利用式(19a)～(19b)得：

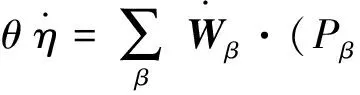
(33)

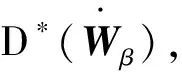
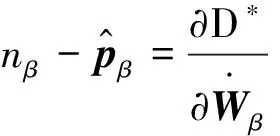
(34)

为了获得液气两相的线性化达西定律，把式(34)中的耗散率势函数D*表达为:

(35)

根据式(34)有(β∈{L,G})：

(36)

从上面的推导过程可以看出，由于本文基于多孔介质工程力学来建立非饱和岩土的线弹性方程，故方程中的各个参数均有明确的物理含义，这就为建立模型参数和常规土工参数之间的换算公式提供了方便。

1.4 模型参数与土工参数之间的关系研究

在岩土力学中，一般都假定组分材料的本构关系与单相时的本构关系相同。令第α组分材料单相时与压强Pα对应的体积模量为Kα，则有：

KRαα=nαKα

(37)

在非饱和岩土土工试验中，保持PL和PG恒定，变化σ，即完全排水和排气，此时可以测定多孔固体的体积模量Kb和剪切刚度G，由式(30)和式(37)可得：

(38a)

(38b)

同时，保持总应力σ和PG恒定，变化PL，可以测定多孔固体体积应变随吸力变化的弹性模量ESr和土-水特征曲线方程Sr=Sr(s)，根据式(30)和式(38a)有：

(39a)

根据总应力σ和气体孔压PG恒定下的土-水特征曲线方程Sr=Sr(s)、式(26b)和式(39a)有：

(39b)

令：

(40a)

(40b)

式中：φ为Biot系数，χ为Bishop系数。把式(38a)～(38b)、式(39a)和式(40a)～(40b)代入到式(30)和式(32a)～(32b)并利用εSv=εS∶1和σm=σ∶(1/3)得：

(41a)

(41b)

(41c)

令：

(42a)

(42b)

(42c)

cSL=φ[χcLL+(1-χ)cLG]

(42d)

cSG=φ[χcLG+(1-χ)cGG]

(42e)

(43a)

M=φχcSL+φ(1-χ)cSG=

φ2[χ2cLL+2χ(1-χ)cLG+(1-χ)2cGG]

(43b)

(43c)

求解式(41a)～(41c)并利用式(42a)～(42e)和式(43a)～(43b)得：

(44a)

(44b)

根据σ=(σ-σm1)和式(44a)并利用式(43c)得：

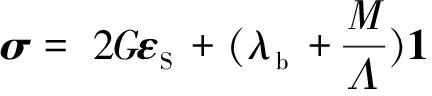
(45a)

(45b)

2 波速公式

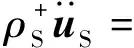
(46a)

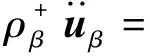
(46b)

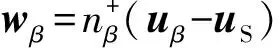
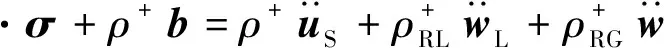
(47a)

(47b)

设液气两相的渗透系数分别为kLL和kGG，液气两相的耦合渗透系数为kLG和kGL，则根据bLL、bLG和bGG与kLL、kLG、kGG和之间的互逆关系可得：

(48a)

(48b)

式(48a)中ηL和ηG为液气两相的黏滞系数。

令eS=εS∶1，把式(45a)～(45b)代入到式(47a)～(47b)得：

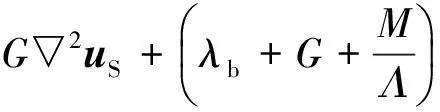
(49a)

(49b)

由于体力只与波动方程的特解有关，其本身不影响体波波速特性，故为简便起见略去式(49a)～(49b)中的体力项，对式(49a)～(49b)求散度并利用ξβ=-▽·wβ得：

(50a)

(50b)

显然，式(50a)～(50b)反映的是压缩波的传播特性，令

{eS,ξL,ξG}={AS,AL,AG}exp[j(ωt-lp·r]

(51)

(52)

式中：

(53a)

(53b)

要使式(52)有非零解，其系数行列式必须等于零，故有：

(54)

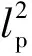
(55)

理论分析有时把式(54)展开较为方便，由此可得：

(56)

式中:

(57a)

(57b)

(57c)

(57d)

求解式(56)同样可获得非饱和土的三个纵波波数。

略去式(49a)～(49b)中的体力项，对式(49a)～(49b)求旋度得：

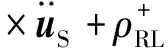
(58a)

(58b)

式(58a)～(58b)反映的是剪切波的传播特性，令

▽×{uS,wF,wG}=

{Bs,BL,BG}exp[j(ωt-lS·r)]

(59)

式中：ω为频率，r为位移矢,lS为波矢量，lS为波数(波矢量模)。把式(59)代入到式(58a)～(58b)得：

(60)

式(60)中：

(61)

故剪切波的相速度和特征衰减系数为：

(62)

3 算例分析双应力耦合效应对波速特性的影响

本节采用数值方法分析双应力耦合效应对非饱和土四个体波波速的影响。模量ESr反映了多孔固体和毛细吸附之间的耦合效应，它与χ之间的关系见式(40a)。为了反映非饱和土双应力变量之间的耦合效应程度，定义双应力变量的耦合效应系数为：

(63)

本节数值分析时土-水特征曲线采用van Genuchten模型，其表达式为[22]：

Sr=[1+(αvgS)nvg]-mvg

(64)

式中：αvg、mvg和nvg是van Genuchten模型的三个参数。相应的渗透系数kLL、kLG、kGL和kGG为：

(65a)

(65b)

kGL=kLG=0

(65c)

式中：κ为本征渗透系数。根据式(39b)、式(40a)和式(64)有：

(66)

根据式(48a)-(48b)和式(65a)～(65c)有：

(67)

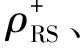
本文选用非饱和土作为算例的研究对象，故固体是土体。数值分析所用的固、液和气的材料弹性模量按常规取值；固、液和气的物理参数、土体骨架的弹性模型参数和van Genuchten模型参数按文献[20]提供的土工参数换算获得，如表1所示。

表1 非饱和土的物理力学参数Tab.1 Physical and mechanical parameters of unsaturated soil

上述规律的力学机理在于：在孔隙流体中，非饱和土的P1和P2纵波波速在一般情况下较大地受KL/nL和KG/nG这两个数值中的较小者影响。由于液体的体积模量KL远大于气体模量KG，当饱和度小于90%时，KG/nG比KL/nL小的多，P1和P2纵波波速主要受气体力学参数控制。当饱和度大于90%时，随着KL/nL与KG/nG数值逐渐接近，液体KL/nL对P1和P2纵波的影响越来越明显，当饱和度接近100%时，KG/nG趋向于无穷大，KL/nL成为较小值，此时P1和P2纵波波速主要受液体力学参数控制。正如学者徐明江和蔡袁强等根据数值分析成果所指出的那样，当饱和度大于90%时，P1和P2纵波从主要受空气体积模量控制过渡到主要受液体体积模量控制，因此，图1中P1和P2纵波波速在这个饱和度区间的变化幅值比较大。固流两相的渗透黏滞效应对P2纵波具有制约作用，故P1纵波波速的变化幅值比P2纵波更加明显。对于P3纵波，当饱和度等于0%时，孔隙中只有气体一种流体，它属于气体饱和土；当饱和度等于100%时，孔隙中变为只有液体一种流体，它属于液体饱和土，由于它们都是饱和土，这两种极端情况下的P3纵波波速均等于零。因此当饱和度从零变化到100%时，P3纵波波速的变化规律是从零开始随着饱和度逐渐增加，到极值后再逐渐减小回归到零。与P1和P2纵波一样，这两个阶段的转折点也在饱和度90%左右。P3纵波波速比较小，只有每秒零点几米。由于基数比较小，即使增加量比较小，相对影响值也比较大。这是当饱和度小于90%时图1中P3波波速变化影响较为明显的原因。当饱和度大于90%时，由于非饱和土逐渐逼近于液体饱和土，第三纵波的波速重新回归为零，这是P3波当饱和度大于90%时波速变化规律较为明显的原因。

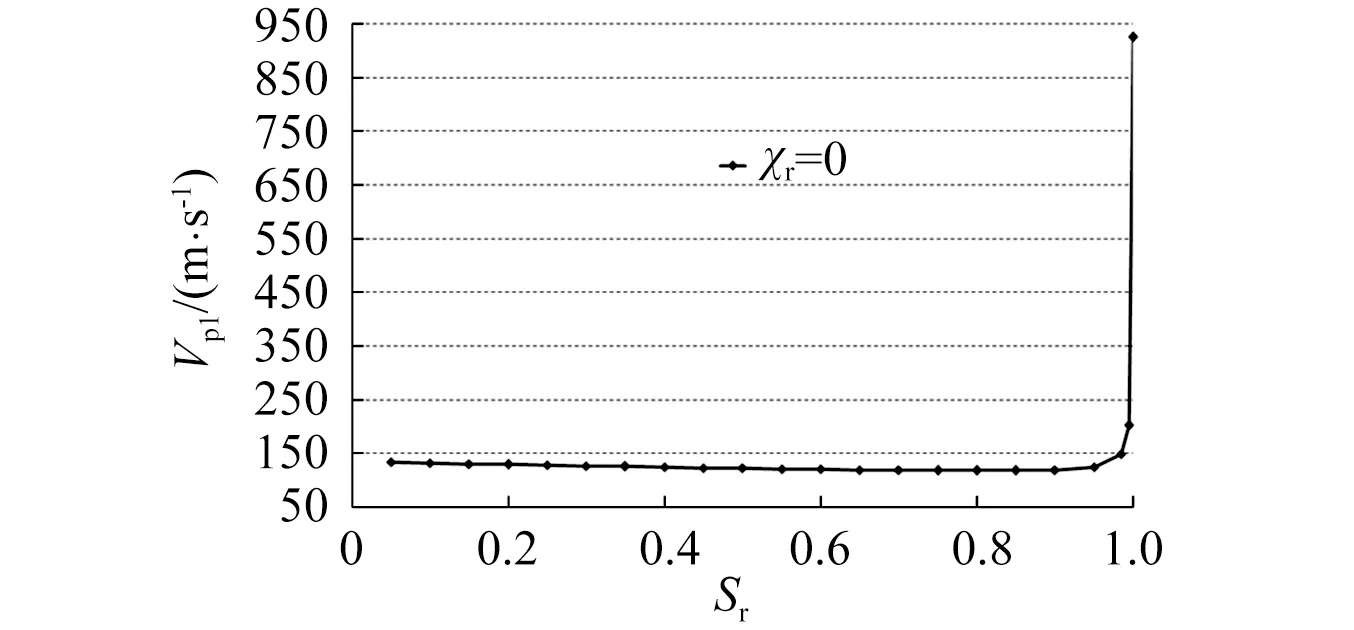
(a) P1 波

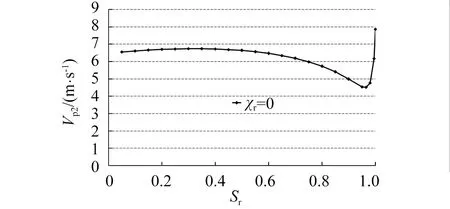
(b)P2 波

(c) P3 波

(d) S 波图1 非饱和土中四种体波随饱和度变化图Fig.1 the velocities of four body waves vary with the saturated degree in unsaturated soil

图1表明当饱和度大于95%时，三种纵波的波速变化剧烈。特别是P1波，当饱和度大于95%后，波速远大于饱和度小于90%时的波速。本文重点是研究双应力变量耦合效应对非饱和土四种体波波速的影响，当饱和度大于95%后非饱和土四种体波波速的剧烈变化会干扰双应力变量耦合效应对非饱和土四种体波波速影响的分析，因此图2和图3中饱和度的取值范围调整为(0.05～0.95)。虽然没有给出饱和度大于95%后双应力变量耦合效应影响体波波速的关系曲线，但根据图2和图3中体波的发展趋势可以容易预测其影响规律。

图2给出了频率20 Hz时双应力变量耦合效应系数对四种体波的影响，从图2中可以看出，双应力变量耦合效应对剪切波波速没有影响，这也可以从公式(60)～(61)中看出。双应力变量耦合效应对P2波和P3波的影响很小，可以忽略不计。当饱和度较小时，双应力变量耦合效应对P1波波速有明显的影响，双应力变量耦合效应系数越大，对P1波波速的影响越明显。但影响程度随着饱和度的增大迅速减小。上述分析表明，当饱和度较小时，双应力变量耦合效应对P1波速的影响是不可忽略的。

(a) P1 波

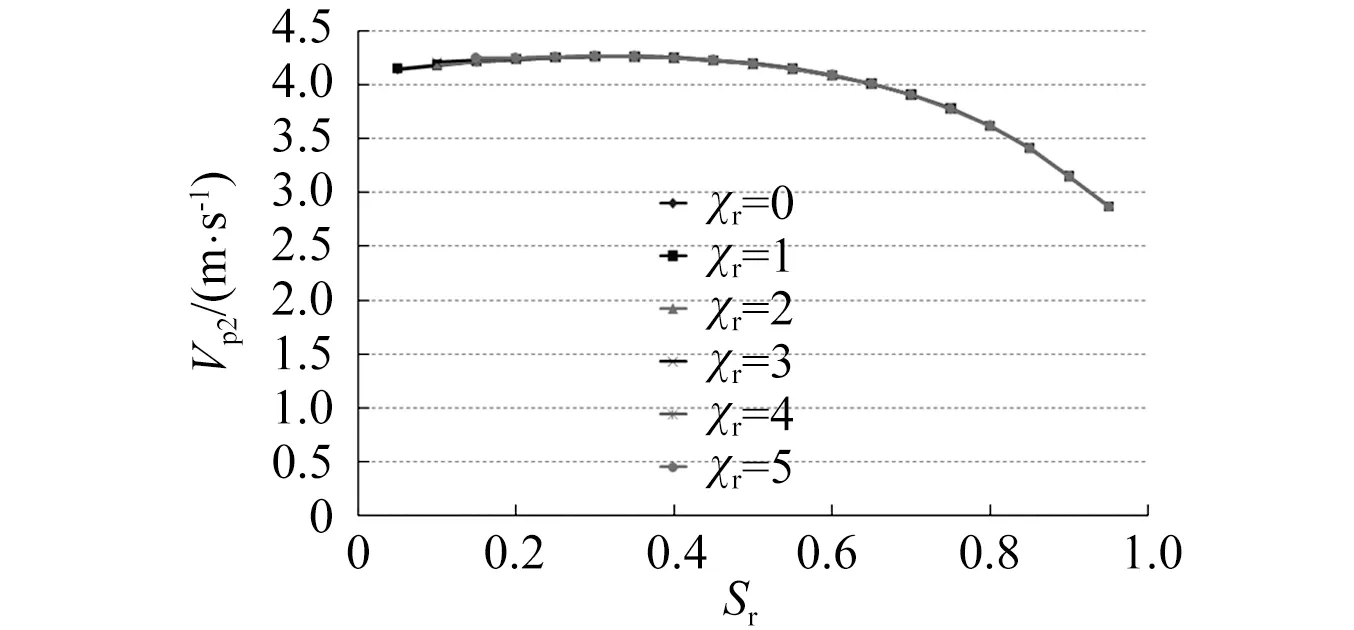
(b)P2 波

(c) P3 波

(d) S 波图2 频率20Hz时四种体波波速随系数变化图Fig.2 the velocities of four body waves vary with the coefficient at the frequency 20 Hz

图3呈现了频率200 Hz时双应力变量耦合效应系数对四种体波的影响规律，所反映的规律特征与图2一致。双应力变量耦合效应对剪切波波速没有影响，对P2波和P3波的影响很小，可以忽略不计。当饱和度较小时，双应力变量耦合效应对P1波波速有明显的影响，但影响程度随着饱和度的增大迅速减小。通过对比图2和图3还可以发现，在低频段，频率对P1波波速和S波波速影响较小，但对P2波和P3波的影响较大。但频率从20 Hz增加到200 Hz时，P2波波速增加了约3倍，P3波的波速增加了约3.2倍。因此，即使在低频段，频率对P2波和P3波波速的影响也无法忽略。

(a) P1 波

(b)P2 波

(c) P3 波

(d) S 波图3 频率200 Hz时四种体波波速随系数变化图Fig.3 the velocities of four body waves vary with the coefficient at the frequency 200 Hz

4 结 论

本文根据非饱和多孔介质工程力学理论，建立了基于双变量理论的非饱和岩土波动理论，获得了以下研究成果：

(1)本文所依据的非饱和多孔介质工程力学理论以岩土力学中常用的应力应变物理量作为建模所用的状态变量，由它推导出的波动方程不但满足弹性力学的互易定理，从而使刚度矩阵具有对称性要求，弥补了当前根据工程法获得的非饱和岩土波动方程刚度矩阵不对称的缺陷；而且容易根据常规土工试验选取模型参数，从而更有利于工程应用。

(2)与不考虑双变量耦合效应的波速传播特性相比，双应力变量耦合效应对非饱和岩土的剪切波波速没有影响。对P2波和P3波的影响很小，可以忽略不计。对P1波波速的影响在饱和度较小时比较明显，耦合效应越大，对P1波波速的影响越明显。但其影响程度随着饱和度的增大迅速减小。

(3)通过对比图2和图3还可以发现，在低频段，频率对P1波波速和S波波速影响较小，但对P2波和P3波的影响较大。但频率从20 Hz增加到200 Hz时，P2波波速增加了约3倍，P3波的波速增加了约3.2倍。因此，即使在低频段，频率对P2波和P3波波速的影响也无法忽略。

参 考 文 献

[1] BIOT M A.Theory of propagation of elastic waves in a fluid-saturated porous solid (I.low-frequency range) [J].J.Acoust.Soc.Am., 1956, 28(2): 168-178

[2] BIOT M A.Theory of propagation of elastic waves in a fluid-saturated porous solid(Ⅱ.higher-frequency range) [J].J.Acoust.Soc.Am., 1956, 28(2): 179-191

[3] BRUTSAERT W.The propagation of elastic waves in unconsolidated unsaturated granular mediums[J].Journal of Geophysical Research, 1964,69(2):243-257.

[4] SANTOS J E, RAVAZZOLI C L, GAUZELLINO P M, et al.Simulation of waves in poro-viscoelastic rocks saturated by immiscible fluids-Numerical evidence of a second slow wave[J].J.Comput.Acoust., 2004, 12(1): 1-21.

[5] 蔡袁强, 李保忠, 徐长节.两种不混溶流体饱和岩石中弹性波的传播[J].岩石力学与工程学报, 2006, 25(10): 2009-2016.

CAI Yuanqiang, LI Baozhong, XU Changjie.Analysis of elastic wave propagation in sandstone saturated by two immiscible fluids [J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(10): 2009-2016.

[6] 徐明江.非饱和土地基与基础的动力响应研究[D].广州：华南理工大学, 2010.

[7] SKEMPTON A W.Effective stress in soils, concrete and rocks[J].Butterwoths: London UK, 1961: 4-16.

[8] VARDOULAKIS I, BESKOS D E.Dynamic behavior of nearly saturated porous media[J].Mechanics of Materials, 1986(5): 87-108.

[9] 徐长节, 史焱永.非饱和土中波的传播特性[J].岩土力学, 2004, 25(3): 354-358.

XU Changjie, SHI Yanyong.Characteristics of wave propagation in unsaturated soils[J].Rock and Soil Mechanics, 2004, 25(3): 354-358.

[10] WEI C F, MURALEETHARAN K K.A continuum theory of porous media saturated by multiple immiscible fluid: I.Linear poroelasticity[J].International Journal of Engineering Science, 2002, 40:1807-1833.

[11] WEI C F, MURALEETHARAN K K.A continuum theory of porous media saturated by multiple immiscible fluids: II.Lagrangian description and variational structure[J].II.International Journal of Engineering Science,2002, 40: 1835-1854.

[12] 黄义，张引科.非饱和土本构关系的混合物理论[J].应用数学和力学, 2003, 24(2): 111-137.

HUANG Yi, ZHANG Yinke.Mixture theory of constitutive relation of unsaturated soil[J].Applied Mathematics and Mechanics, 2003, 24(2): 111-137.

[13] CHEN W Y, XIA T D, HU W T.A mixture theory analysis for the surface-wave propagation in an unsaturated porous medium[J].International Journal of Solids and Structures, 2011, 48(16): 2402-2412.

[14] 弗雷德隆德 D G, 拉哈尔佐 H.非饱和土土力学[M].陈仲颐, 张在明, 陈愈炯, 译.北京: 中国建筑工业出版社, 1997.

[15] HOULSBY G T, PUZRIN A M.Principles of Hyper- plasticity[M].Springer: London, 2006:211-239.

[16] BORJA R I.On the mechanical energy and effective stress in saturated and unsaturated porous continua[J].International Journal of Solids and Structures, 2006, 43: 1764-1786.

[17] 胡亚元．非饱和多孔岩石的热力学本构理论研究[J].浙江大学学报工学版, 2017,51(2): 255-263.

HU Yayuan, Thermodynamics-based constitutive theory for unsaturated porous rock[J].Journal of Zhejiang University (Engineering Edition), 2017,51(2): 255-263.

[18] BOWEN R M.Theory of mixture.In AC Eringen (ed): Continuum Physics, Vol III[M].Academic Press: New York, San Francisco, London, 1976

[19] BISHOP A W.The principle of effective stress[J].Teknisk Ukeblad, 1959, 106(39): 113-143.

[20] WHEELER S J, SHARMA R S, BUISSON M S R.Coupling of hydraulic hysteresis and stress-strain behavior in unsaturated soil[J].Geotechnique, 2003,53(1): 41-54.

[21] 黄筑平.连续介质力学基础[M].北京:高等教育出版社, 2003:78-122.

[22] VAN GENUCHTEN M T.A closed form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Science Society of America Journal, 1980, 44(5):892-898