盘绕式伸展臂非线性振动力学分析
2018-05-28樊鹏玄陈务军张祎贝
樊鹏玄,陈务军,张祎贝,赵 兵
(上海交通大学 空间结构研究中心,上海 200240)
盘绕式伸展臂作为支撑构件广泛应用于太阳翼、太阳帆、空间站等航天器[1-2]。具有构造简捷、比刚度大、收纳率高、成本低等优点,是可展结构中高效、可靠的典范。盘绕臂在航天器中的重要作用决定其振动分析与控制是航天工程中的要点。目前针对盘绕臂的研究多集中于结构稳定性与屈曲荷载[3-4]、展开与收纳的动静力学特性[5-6]。振动分析方面,McEachen等[7-9]计算了盘绕臂线性振动频率并进行了试验验证。戈东明、陈务军等[10-12]进行了盘绕臂展开状态的线性模态分析。韩建斌等[13]用缩小弹性模量的方法描述三角框受压屈曲状态,采用分段线性模型描述加劲索松弛前后的盘绕臂振动力学性能,对加劲索松弛前后的盘绕臂分别进行了模态分析。
盘绕臂属柔性可展开结构体系,结构刚度受加劲索预应力影响较大。加劲索中的预应力对结构具有加载作用,引发P-Δ效应,要准确获取预应力对盘绕臂自振频率、模态的影响须考虑此几何非线性的影响;航天器在太空中受到冲击荷载以及盘绕臂展开结束时,盘绕臂将发生加劲索高频交替张弛的大幅度振动,故考虑大幅振动下状态非线性因素进行振动分析与控制也是盘绕臂设计的基础。
以往的报道尚未对预应力加载作用引发P-Δ效应的影响以及大幅振动下加劲索高频交替张弛引发的状态非线性进行研究,文章将针对两个问题分别进行计算。首先采用几何精确理论及结构屈曲分析理论推导加劲索的预应力取值范围,然后进行振动分析。小幅振动时,采用增量有限元法考虑预应力加载作用引发几何非线性对结构模态和频率的影响,得出小幅振动下使结构自振频率最大的预应力取值,并绘制设计用“频率-预应力-直径”参考面,在参考面内可对加劲索的预应力、直径等参数进行主动设计;大幅振动时,利用显式动力学积分解决加劲索状态非线性中刚度矩阵奇异的问题并获取振动时程响应,采用自编制的动力时程信号处理程序,提取大幅振动的频率、模态,并揭示大幅振动时加劲索使盘绕臂振幅迅速衰减的作用机理。可作为大幅非线性振动控制的参考依据。
1 盘绕式伸展臂非线性振动分析方法
以振动中加劲索是否松弛为判定依据,将盘绕臂振动问题为两类:一是加劲索不发生松弛的小幅振动,二是加劲索发生高频张弛切换的大幅振动。
1.1 小幅非线性振动
在加劲索预应力的加载作用下盘绕臂形成静力平衡体系,其振动以此为初始状态。随预应力增大,盘绕臂变形增大,预应力加载产生的P-Δ效应增强。可基于非线性有限元法,将P-Δ效应作为荷载刚度纳入计算,计算流程如下:
(1) 建立刚度矩阵和质量矩阵
加劲索刚度组成[14]
KC=KLC+KNLC
(1)
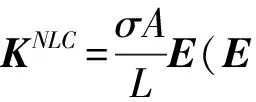
纵杆及横杆(采用梁单元)刚度组成[15-16]
KB=KEB-KPB
(2)
式中:KEB是弹性刚度阵(与EI和l有关);KPB是荷载刚度阵(与作用在单元两端的力P和l有关)。
依据有限元法刚度矩阵集成规则,集成得整体刚度

(3)
将各个单元质量集中到节点,根据节点编号集成得到集中质量矩阵M。
(2) 建立特征值方程并迭代求解
不考虑系统阻尼,可建立广义特征值方程式(4),采用子空间迭代提取考虑P-Δ效应的频率及模态
Kφ-ω2Mφ=0
(4)
式中:φ为固有振型;ω为固有频率
如式(3),KNLC使盘绕臂刚度增大,KPB使其刚度减小,故存在一个预应力值使盘绕臂自振频率取极值。取不同预应力值代入式(4),求解结构频率及模态,可找到使结构频率最大的预应力。
1.2 大幅非线性振动
大幅振动中,加劲索张紧时盘绕臂是几何不变结构体系。但松弛时,成为几何可变体系,刚度矩阵奇异,无法基于式(4)进行特征值迭代。文章采用动力学响应直接积分,获取盘绕臂自由振动的时程响应,再进行时程信号处理来提取大幅振动参数。
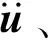

(5)
(6)
求解式及得到时程响应,利用快速傅氏变换(Fast Fourier Transform, FFT)及随机子空间法[19](SSI/data)编制时程信号处理程序,用于提取自振频率及模态。后文分析指出,基于时域的SSI/data法虽可同时得到自振频率及模态,但振动信号中夹杂大量加劲索局部振动带来的干扰,无法确定可靠的振动参数。利用基于频域的FFT识别法处理盘绕臂自由端的振动信号,能提取出更准确的频率值。结合两种方法提取大幅非线性振动模态及频率。图1给出计算流程。
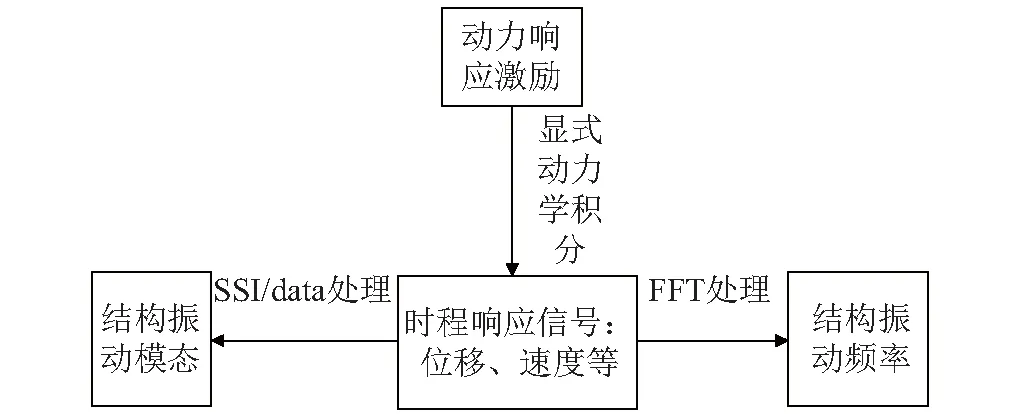
图1 盘绕式伸展臂大幅度非线性振动计算Fig.1 Nonlinear large amplitude vibration analysis
2 加劲索预应力取值范围
加劲索预应力对盘绕臂有加载作用(图2),展开状态下,设每根加劲索预应力σ0为,加劲索截面积为A,则加劲索作用力F=σ0A。在加劲索预应力作用下纵杆应保持平直,三角框处于受压的微弯曲状态。
图2中BC节段受到4个加劲索力,根据力的矢量和原理将索力投影到纵杆轴线方向及三角框平面内,作用在纵杆上的轴压力
F1=2Fcosβ
(7)
该力作用下纵杆不发生屈曲
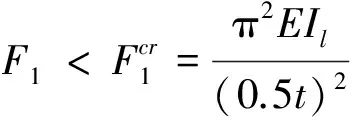
(8)
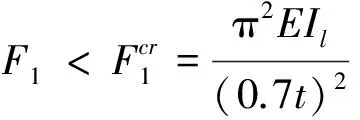
(9)
式中:t为盘绕臂节距;EIl为纵杆截面抗弯刚度。中间节段纵杆等效于两端固支杆,端部节段等效于一端固支一端铰支。

图2 加劲索作用力Fig.2 The force from the cable
加劲索作用在三角框上的力转化为Ft,指向形心(图3)
(10)

图3 三角框大挠度后屈曲Fig.3 Post-buckling of triangle battern
三角框受压发生变形,基于几何精确理论及势能驻值原理将平衡方程建立在变形后的位形上。总势能见式(11),平衡方程见式(12)。
(11)
(12)
式中:b是三角框边长;EIt为横杆截面抗弯刚度;s为沿横杆的弧坐标;φ为横杆变形后切线与原始位置轴线方向的夹角。
求解非线性微分方程式(12)可得到三角框受压弯曲后变形。以φ近似替代sinφ,可求解出小变形时三角框受压临界屈曲荷载
(13)
基于式(7)~式(9)、式(13)可求出加劲索预应力应满足的条件
(14)
3 盘绕臂振动力学特性计算
3.1 盘绕式伸展臂建模
非线性有限元分析及显式动力学积分运算过程可直接利用ABAQUS软件进行,采用以往的盘绕臂设计参数(见表1[20])建立盘绕臂计算模型,盘绕半径r为150 mm,总长1 884 mm,分为9节(图4)。

图4 盘绕式伸展臂整体模型Fig.4 Numerical model of coilable mast
加劲索用多段铰接杆单元建模,并设置只能承受轴向拉力。
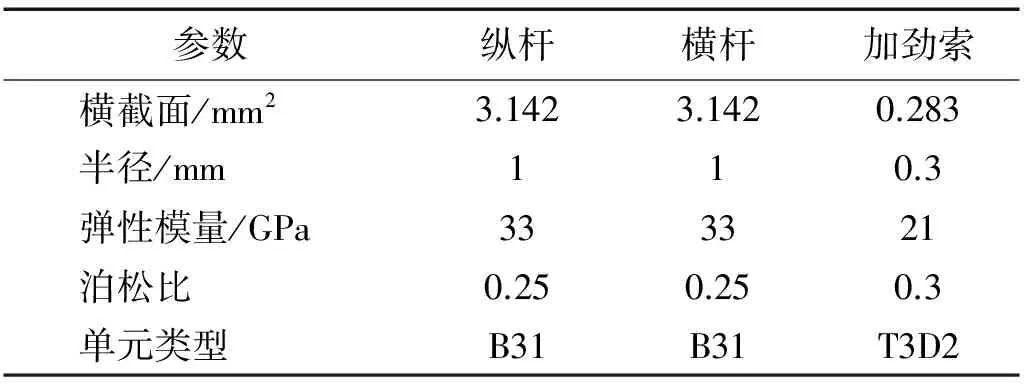
表1 模型参数Tab.1 Material properties
3.2 小幅度非线性振动计算
根据式计算出预应力范围是:8.60~33.32 MPa,计算时对加劲索施加预应力进行几何非线性静力分析以获取加载后的平衡态,基于该状态集成弹性刚度与荷载刚度阵,采用子空间迭代法,求解自振模态及频率。图5给出预应力从1 MPa到35 MPa的盘绕臂频谱(增加1 MPa计算1次),可分为3段,各段特性:
A段:加劲索预应力小于等于8 MPa,三角框尚未屈曲,加劲索是刚度薄弱项。图6给出5 MPa时结构1阶模态,整体表现为弯曲。据前文1.1部分的分析,此段预应力增大使KC的增大超过KB的减小,故预应力增大,盘绕臂一阶频率上升。
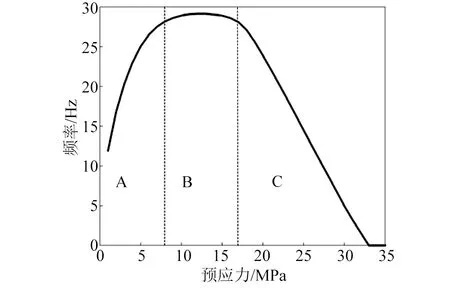
图5 预应力与自振频率曲线Fig.5 Relationship between prestress and frequency
图6 预应力5 MPa下盘绕臂1阶模态Fig.6 First-order mode of coilable mast of 5 MPa prestress
B段:加劲索预应力大于等于9 MPa,三角框进入后屈曲阶段。此段KC的增大与KB的减小持平,盘绕臂整体刚度保持水平。图7给出预应力15 MPa时盘绕臂的1阶模态,整体表现为弯曲,但三角框成为盘绕臂刚度弱项。

图7 预应力15 MPa下盘绕臂1阶模态Fig.7 1st mode of coilable mast in 15 MPa prestress
C段:随预应力增加,P-Δ效应更加显著,此时KC的增大小于KB的减小,整体刚度下降,自振频率降低。33 MPa力下结构的1阶频率降低为0(表 2),相应模态(图8)为纵杆屈曲屈曲模态。这与式(14)的理论推导恰好吻合。

图8 预应力33 MPa下盘绕臂1阶模态Fig.8 1st mode of coilable mast in 33 MPa prestress
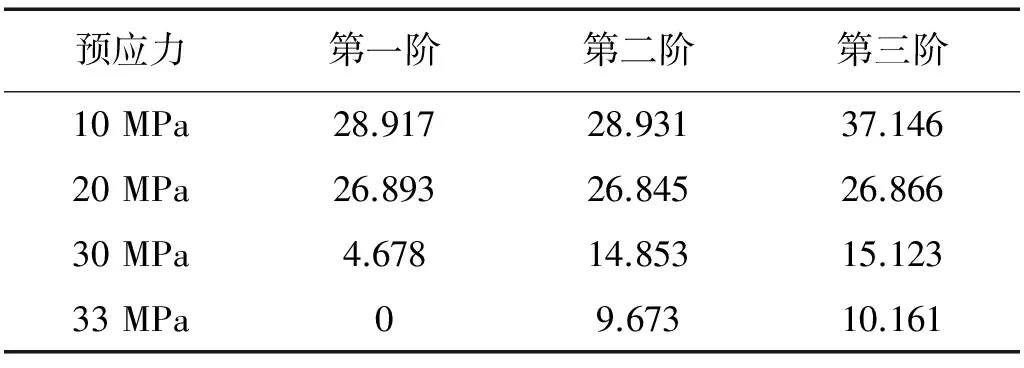
表2 结构固有频率Tab.2 Natural vibration frequency Hz
计算不同直径加劲索、不同预应力下盘绕臂自振频率,绘制图9,可得到设计用“频率-预应力-直径”包络面(以O为顶点的扇形),设计时应使加劲索直径、预应力落在面中,保证结构刚度最大。
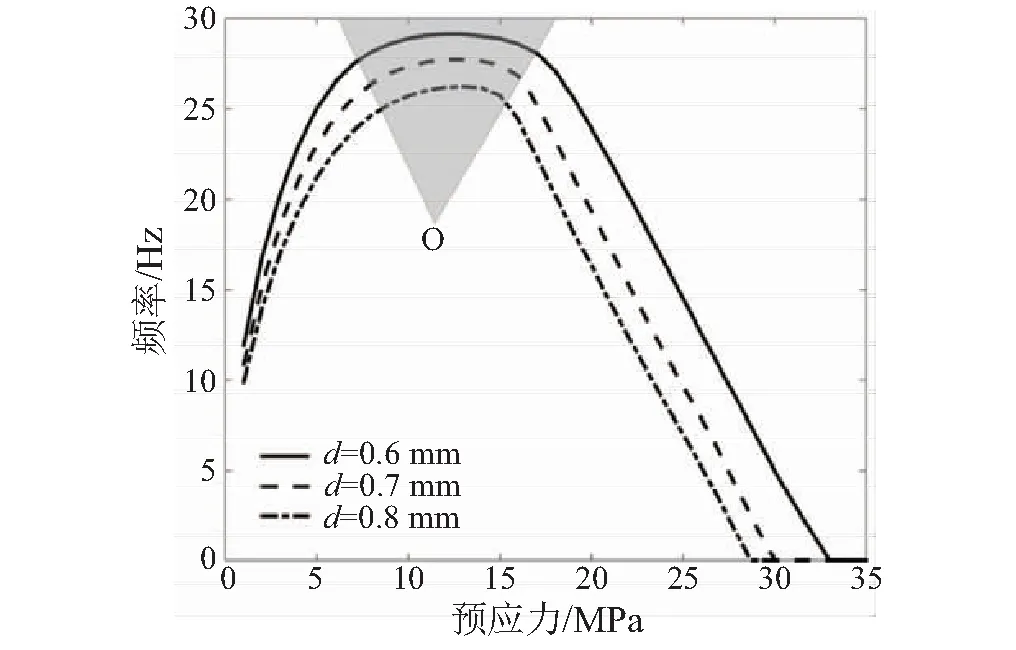
图9 不同直径加劲索的盘绕臂频率曲线Fig.9 Frequency curves of different cable diameters
3.3 大幅度非线性振动计算
3.3.1 动力学响应时程积分
如图10,固定端板O点,在自由端施加Y向位移δ,使盘绕臂发生变形U。施加位移δ时,靠近固定端的加劲索先松弛,随δ增大,加劲索松弛的节数增多(表3)。此外,预应力小的加劲索更容易出现松弛;当δ大于或等于5 mm时,9节加劲索全部松弛。

图10 振动前状态Fig.10 Deformation before vibration
令δ等于5 mm,使盘绕臂自由振动并进行动力学响应时程积分,绘制自由端Y向位移U-t曲线于图11,盘绕臂的振幅从5 mm开始衰减,最后稳定在1.4 mm左右。
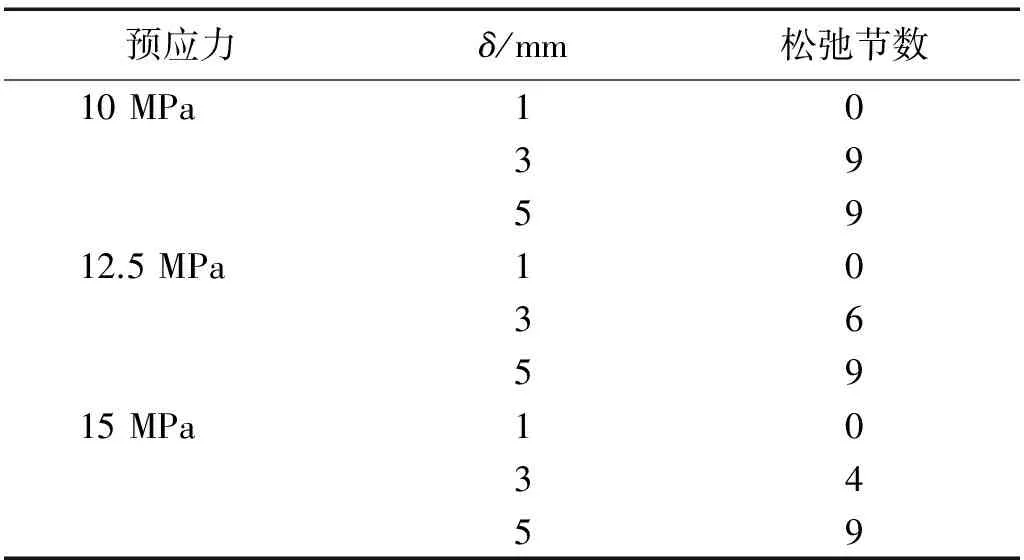
表3 不同δ下松弛的节数Tab.3 Number of relaxation steps with various δ

图11 盘绕式伸展臂自由端动力学响应Fig.11 Dynamic response of free-tip
3.3.2 频率提取及模态识别
取各节三角框端部节点的位移时程数据用于计算结构模态,结构变形主要在y,z方向,x向变形很小,为提高计算效率,取各节点y,z向位移响应进行模态识别。将3.3.1中仿真得到的数据代入基于MATLAB平台编写的SSI/data程序中计算,采用频率、阻尼及振型三重稳定判定准则来判定第j阶模态是否稳定,设置容差见式(15)。
(15)
式中:fi,j、ξi,j分别表示选取系统阶次为i时,识别的第j阶模态的频率和阻尼比,MACj表示第j阶模态的置信准则(Modal Assurance Criterion,MAC),定义见式(16)。
(16)
式中:ψi,j表示当选取系统阶次为i时,识别的第j阶模态的振型。
取预应力为10 MPa的进行计算,将识别的系统阶次定为2 940~3 000。取前240阶模态(频率<40 Hz)绘制稳定图12。图中模态十分密集,大部分是加劲索局部模态,无法从图中直接确定主结构模态。故借助FFT方法得到频响曲线来判定所需提取的结构模态。
基于图11的位移时程信号,利用FFT处理得到盘绕臂自振频率见表4(表中“小幅振动”指前文3.2部分计算结果)。可看出12.5 MPa预应力下的盘绕臂在小幅振动时频率最大,同时在大幅非线性振动下频率也最大。由此得出整体刚度越大,抵抗大幅度振动并维持刚度不降低的能力越强。
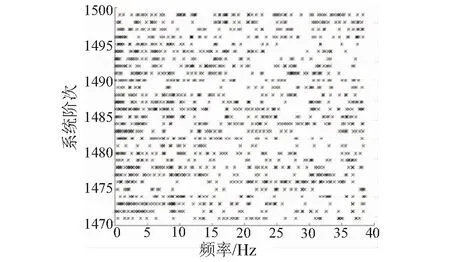
图12 稳定图Fig.12 Stability diagram

表4 结构自振频率Tab.4 Natural vibration frequency Hz
振幅衰减区的自振频率为22.73 Hz,在稳定图14中,22.67 Hz附近稳定点较集中,以此为衰减区模态,振型为图14。该阶模态包含加劲索交替张弛的非线性现象,振型比较复杂同法可确定振幅稳定区结构频率为24.97 Hz,振型为结构的一阶弯曲变形。

图13 22.73 Hz附近的稳定图Fig.13 Stability diagram near 22.73 Hz

图14 22.67 Hz对应的振型Fig.14 Vibration mode of 22.67 Hz
3.3.3 结果讨论
(1) 能量守恒验证
显式动力学积分采用中心差分来近似积分,易出现累积误差。通过验证盘绕臂振动中的能量守恒来评价计算是否正确[21]。结构大幅非线性振动中的能量关系应满足式(17)
ETOTAL=EK+EI
(17)
式中:EK为动能;EI为内能;ES为应变能。

图15 振动过程中能量守恒验证Fig.15 Verification of energy conservation in vibration
能量守恒定律要求振动中总能量等于常数。由于体系处于弹性范围,还应有EI=ES。图15显示在振动中总能量最大值57.39 J,最小值56.97 J,平均值57.26 J,最大偏差0.51%,基本守恒;内能和应变能也基本相等。满足能量守恒定律;振动稳定后,盘绕臂总能量在动能和应变能间相互转换,保持动态平衡。
(2) 时程信号处理法与特征值迭代法对比
采用子空间迭代法进行特征值迭代考察的是结构刚度矩阵的固有属性,当结构尺寸、材料参数、加劲索的预应力确定后,特征值迭代所求解出的结果是唯一确定、静态不变的,表征结构小幅振动特性。
时程信号处理不仅可以考察不同振幅、不同预应力下加劲索发生不同程度松弛后的振动参数,也可考察同一次大幅振动中,由于振幅衰减使加劲索松弛节数越来越少,刚度特性发生改变的动态过程。
当然,采用时程信号处理同样可计算小幅振动参数,取预应力10 MPa、12.5 MPa、15 MPa,采用时程信号处理法求解得到自振频率分别为28.36 Hz、28.57 Hz、28.40 Hz,与特征值迭代的结果(表4第4列)相对误差分别为1.97%、1.98%、1.70%,两种法计算结果的统一性再次验证了计算的正确性。
(3) 加劲索作用机理
文中计算均未考虑阻尼,图11显示大幅振动有振幅衰减阶段,而图16显示小幅振动无振幅衰减段。为揭示加劲索的 “稳定索”功能,令δ等于5 mm,计算无索盘绕臂自振响应并进行对比(图17)。结果显示随时间推移,振幅未出现衰减。这表明只有存在加劲索,才会发生振幅衰减现象。

图16 盘绕式伸展臂小幅振动位移时程Fig.16 Displacement response of small amplitude vibration

图17 无加劲索伸展臂振动位移时程Fig.17 Displacement response of non-cable mast
振动中加劲索受拉张紧时,纵杆对其做正功,纵杆变形能转变成加劲索变形能,加劲索松弛后,加劲索的变形能又转变成加劲索局部自振的动能。从图15的能量转化可看出,如此往复5个周期,体系能量最终转变为整体结构中纵横杆和劲索的应变能、动能,以及加劲索局部自振动的动能,并处于动态平衡。
(4) 试验验证
制作盘绕臂模型进行模态测试来验证文章的计算方法见图18。制作的盘绕臂参数见表1,由于加工条件限制,减小加劲索直径为0.3 mm。

图18 盘绕臂模态试验装置Fig.18 Modal test facility of coilable mast
采用扫描激光测振仪测试盘绕臂的自振频率及模态。在盘绕臂不同位置施加振动激励,使其分别发生弯曲、扭转、弯曲+扭转三种形式的振动。在盘绕臂一个面的各层节点上共布置20各信号测点,对盘绕臂进行振动扫频,扫频范围为0~25 Hz。得到不同振动形式下频谱响应曲线峰值点与相应模态见表5。综合三种振动模式的测试结果,得到盘绕臂的各阶固有频率及对应模态见表 6(表 5中阴影部分)。
试验中施加到加劲索中的预应力约为20 MPa,盘绕臂的最大振幅为0.4 mm,加劲索未发生松弛,故计算中采用小幅非线性振动分析方法。由于结点采用铸铁制作,相对盘绕臂整体结构有较大质量,故在计算中考虑节点质量,并以集中质量点形式添加到计算模型中,每个节点质量为28.7 g。计算结果表明,节点集中质量的存在使盘绕臂自振频率有较大降低。
从表6可看出计算结果的模态基本与试验结果吻合,但自振频率偏大约3%。这是由于加工制作的结点存在间隙,导致实际结构刚度偏小;同时计算中未考虑结构阻尼也会导致计算结果偏大。总体来看计算值与实验值较为接近,计算方法是可靠的。

表5 盘绕臂振动响应曲线峰值点及对应模态Tab.5 The peak points and modals of vibration response curve of coilable mast Hz

表6 自振频率及模态试验与计算结果对比Tab.6 Comparison of the experiments and simulation in natural frequencies and modal Hz
4 结 论
盘绕臂的振动特性不仅决定振动控制措施,还决定加劲索的预应力取值。文章通过几何精确理论和屈曲分析理论的推导,得出静力条件下加劲索预应力被动满足的式;基于非线性有限元法,文章计算并总结了P-Δ效应对盘绕臂小幅振动的影响,总结出设计用“频率-预应力-直径”参考面,预应力在该取值范围内可进行主动设计以达到对结构刚度、振动特性进行主动控制的目的;基于显式动力学积分获取结构振动时程信号,采用自编制的时程信号处理程序来获取大幅振动的模态、频率,在大幅振动控制中可起到参考作用,并揭示了大幅振动时加劲索有助于振幅迅速衰减的机理。文章提出的计算方法也可作为预应力张拉结构体系非线性振动分析的参考案例。
参 考 文 献
[1] 丁锋.典型杆状构架式展开机构[J].上海航天,2006(1): 35-40.
DING Feng, Typical mast-liked deployment mechanism with truss structure[J].Aerospace Shanghai, 2006(1): 35-40.
[2] MCEACHEN M, TRAUTT T.Confirmation of new analytics for ultra-light lattice column strength using a 40-m flight article[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.4-7 May 2009, Palm Springs, California.
[3] 刘涛, 韩涵, 冀宾,等.盘绕式伸展机构非线性屈曲模式的试验研究与数值仿真[J].南京航空航天大学学报, 2015, 47(6): 897-903.
LIU Tao, HAN Han, JI Bin, et al.Experimental investigation and numerical simulation on nonlinearlinear buckling mode of coil-able mast[J].Journal of Nanjing University of Aeronauticus & Astronautics, 2015, 47(6): 897-903.
[4] 刘涛, 金玉龙, 吕榕新,等.FASTMast伸展机构屈曲模式的理论分析与试验[J].宇航学报, 2015(4): 404-409.
LIU Tao, JIN Yulong, LÜ Rongxin, et al.Theoretical analysis and experimental investigation on the buckling mode of FASTMast deployable truss structure[J].Journal of Astronautics, 2015(4): 404-409.
[5] 薛纭, 刘昭.受圆柱面约束弹性细杆的摩擦平衡分析[J].力学季刊, 2016(1): 139-148.
XUE Yun, LIU Zhao.Analysis of equilibrium with friction of an elastic rod constrained by a cylindrical surface[J].Chinese Quarterly of Mechanics, 2016(1): 139-148.
[6] 张金龙.盘绕式空间伸展臂力学行为研究[D].上海:上海交通大学, 2014.
[7] LUBINSKI A, ALTHOUSE W S.Helical buckling of tubing sealed in packers[J].Journal of Petroleum Technology, 2013.
[8] MCEACHEN M.Validation of SAILMAST technology and modeling by ground testing of a full-scale flight article[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 4-7 January 2010, Orlando, Florida.
[9] MCEACHEN M, TRAUTT T, MURPHY D.The ST8 SAILMAST Validation Experiment[C]//46th AIAA/ASME/ASCE/AHS/ ASC Structures, Structural Dynamics&Materials Conference, 18-21 April 2005, Austin, Texas.
[10] 戈冬明, 陈务军, 付功义, 等.盘绕式空间可展折叠无铰伸展臂的屈曲分析理论研究[J].计算力学学报, 2007, 24(5): 615-619.
GE Dongming, CHEN Wujun, FU Gongyi, et al.Buckling analysis on hingeless coilable mast[J].Chinese Journal of Computational Mechanics, 2007, 24(5): 615-619.
[11] 戈冬明, 陈务军, 董石麟.盘绕式空间可展伸展臂展开状态结构动力研究[C].第四届海峡两岸结构与岩土工程学术研讨会, 杭州: 2007.
[12] 戈冬明.盘绕式空间可展伸展臂折叠屈曲机理与结构动力分析[D].上海:上海交通大学,2007.
[13] 韩建斌, 黄海, 马海波.考虑斜拉索松弛的盘绕式伸展臂振动模型[J].北京航空航天大学学报, 2014, 40(7): 970-977.
HAN Jianbin, HUANG Hai, MA Haibo.Vibration model of coilable mast considering slack diagonals[J].Journal of Beijing University of Aeronautics and Astronautics,2014, 40(7): 970-977.
[14] 陈政清,杨孟刚.梁杆索结构几何非线性有限元-理论、数值实现与应用[M].北京: 人民交通出版社, 2013.
[15] 杜家政, 王丽, 罗明智.基于屈曲分析结果的单元荷载刚度矩阵计算[C].北京力学会第18届学术年会.北京: 2012年2月.
[16] 张年文.荷载刚度矩阵的推导和应用[J].茂名学院学报, 2004, 14(3): 45-48.
ZHANG Nianwen.Derivation and application of geometric stiffness matrix[J].Journal of Maoming College, 2004, 14(3): 45-48.
[17] 王勖成.有限单元法[M].北京: 清华大学出版社, 2003.
[18] 刘晶波,杜修力.结构动力学[M].北京: 机械工业出版社, 2005.
[19] 祁泉泉.基于振动信号的结构参数识别系统方法研究[D].北京:清华大学, 2011.
[20] 陈务军,张淑杰.空间可展开结构体系与分析导论[M].北京: 中国宇航出版社, 2006.
[21] 庄茁,由小川,廖剑晖,等.基于ABAQUS的有限元分析和应用[M].北京: 清华大学出版社, 2009.
[22] BAB S, KHADEM S E, ABBASI A, et al.Dynamic stability and nonlinear vibration analysis of a rotor system with flexible/rigid blades[J].Mechanism and Machine Theory, 2016,105: 633-653.
[23] HOU L, CHEN Y, CAO Q, et al.Nonlinear vibration analysis of a cracked rotor-ball bearing system during flight maneuvers[J].Mechanism and Machine Theory, 2016,105: 515-528.
[24] BAB S, KHADEM S E, ABBASI A, et al.Dynamic stability and nonlinear vibration analysis of a rotor system with flexible/rigid blades[J].Mechanism and Machine Theory, 2016, 105: 633-653.
[25] SOLTANI P, SABERIAN J, BAHRAMIAN R.Nonlinear vibration analysis of single-walled carbon nanotube with shell model based on the nonlocal elasticity theory[J].Journal of Computational & Nonlinear Dynamics, 2015, 11(1): 011002.
