基于自适应时频滤波的变转速齿轮故障特征提取

陈向民，张 亢，晋风华，李录平

(长沙理工大学 能源与动力工程学院，长沙 410076)

齿轮是旋转机械中的重要动力传输部件。长时间、高负荷地运行容易引起齿轮出现局部故障。齿轮出现局部故障时，其振动信号中会产生以转频及其倍频为调制频率的调幅调频信号[1]。如何从原始振动信号中将包含齿轮局部故障信息的调幅调频信号提取出来是诊断齿轮故障的关键。

对于恒定转速下的齿轮故障信号分离，常用的信号分析方法主要有共振解调[2]、小波分析[3-4]、EMD/EEMD[5-6]、LMD[7-8]等。这类方法的共同特点是采用类似于带通滤波的方式对信号进行分析，将包含故障信息的信号成分分离出来，对于恒定转速下的故障信号分析取得了较好的效果。但对于频率大范围波动的非平稳信号(如机器的启停、工况的改变等)，若直接采用该类方法进行故障信号提取，则分析结果不太理想[9]。

时频滤波通过先采用时频分析方法将信号展开为时间-频率的联合函数(即时频分布)，再在时频域对信号进行滤波分析，可有效提取时变非平稳信号成分，已成为非平稳信号分析的一种重要方法。常用于时频滤波的时频分析方法有短时傅里叶变换，Wigner-Ville变换、Gabor变换[10]，S变换[11]等，其中，S变换因不含交叉项，且保留了信号的绝对相位信息，因而，近年来被用于非平稳信号的时频滤波分析[12-14]。

时频滤波的基本原理是根据分析信号的频率变化特点，在时频域选取合适的时频区域(即时频滤波器)进行滤波分析。对于变转速下的齿轮故障信号，其时频滤波器的设计主要包括中心频率和带宽两个部分，其中，中心频率的选取是关键[15]。而对于齿轮故障信号的时频滤波器的中心频率一般选取为齿轮的啮合频率。因此，如何精确的将啮合频率曲线从齿轮故障信号中提取出来对其时频滤波器的设计至关重要。CPP方法是Candes等[16]提出的一种非平稳信号频率曲线估计方法，具有较高的频率估计精度，且具有很强的抗噪能力，近年来被用于机械故障诊断，取得了较好的效果[17-18]。

基于上述分析，本文将CPP方法与S变换相结合，提出了基于CPP与S变换的自适应时频滤波方法，并将其应用于齿轮故障特征提取中。算法仿真和应用实例表明，自适应时频滤波方法可根据齿轮故障信号的频率变化特点，自适应地改变中心频率和带宽，能有效分离出齿轮故障信号成分，并提取齿轮故障特征，且滤取的信号无相位畸变。因此，该方法非常适合于变转速下的非平稳信号分析。

1 CPP算法

CPP算法采用的多尺度线调频基元函数库为

D(haμbμI)={haμbμI(t)}={KaμbμIe[-i(aμt+bμt2)]LI(t)}

(1)

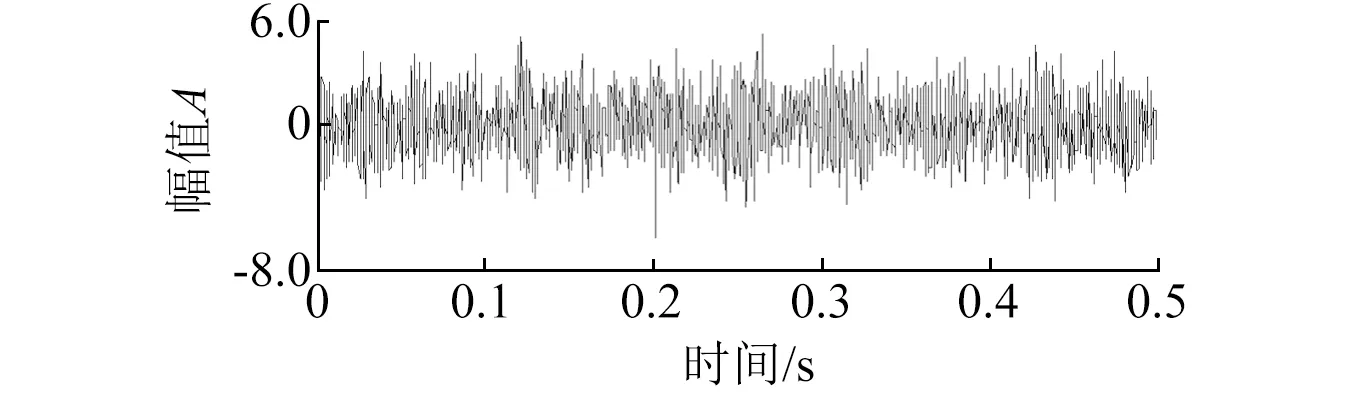
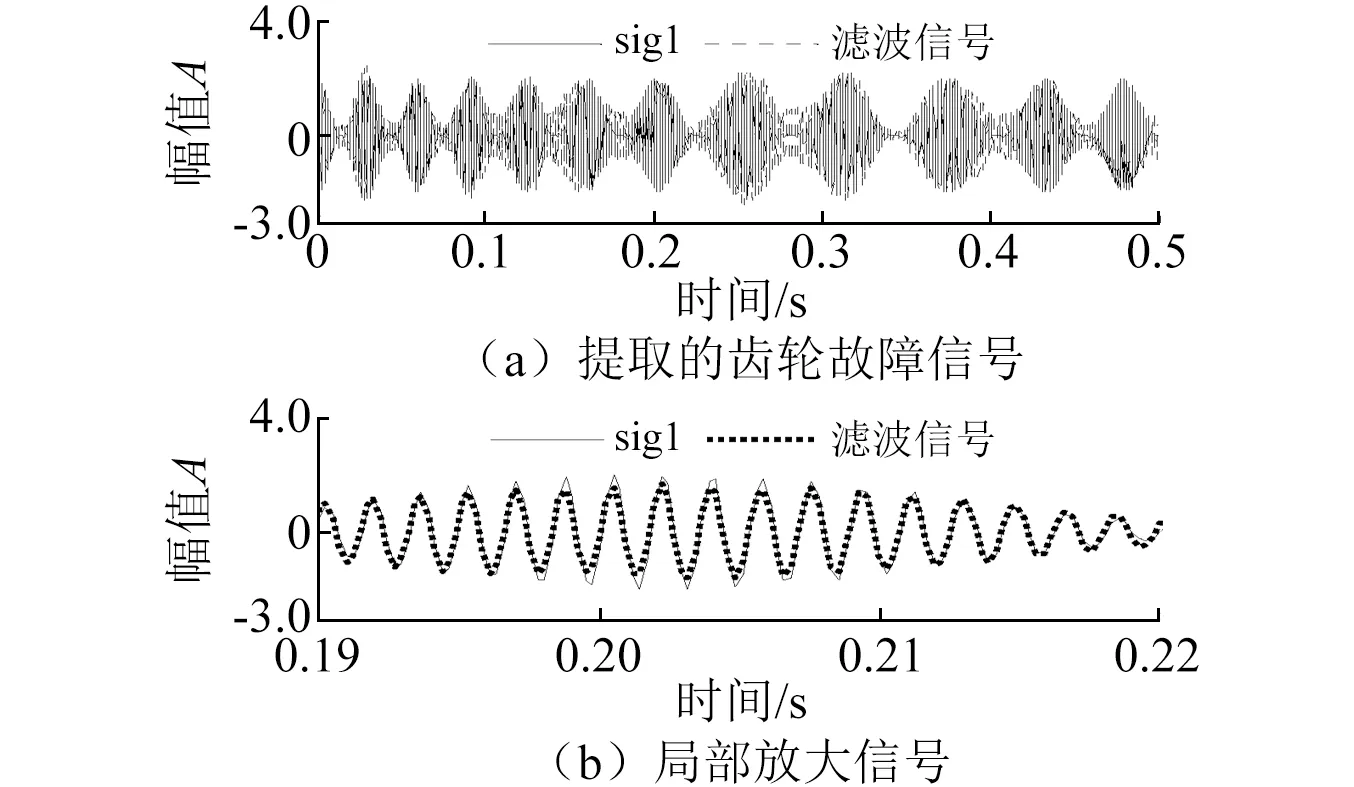
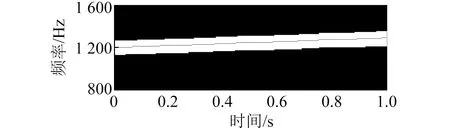
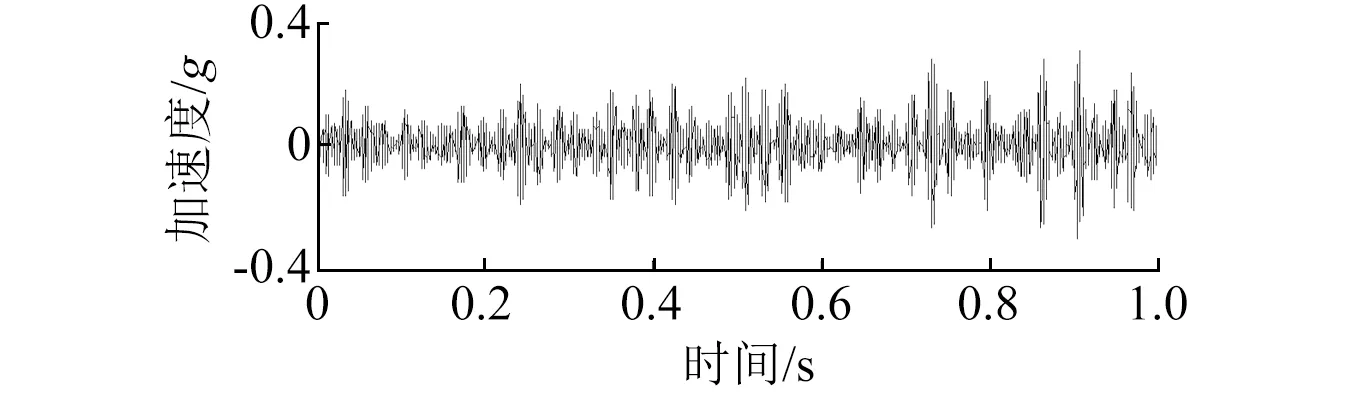
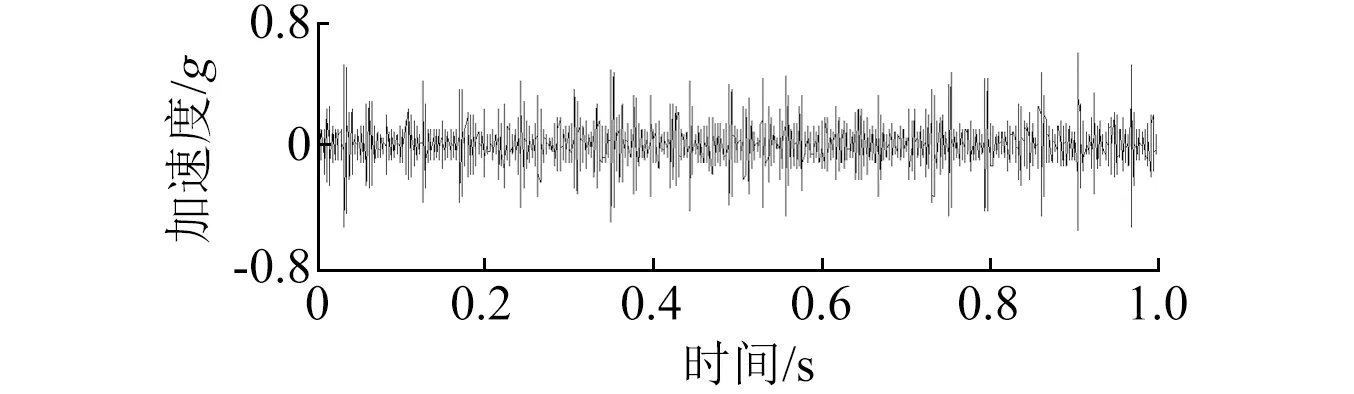
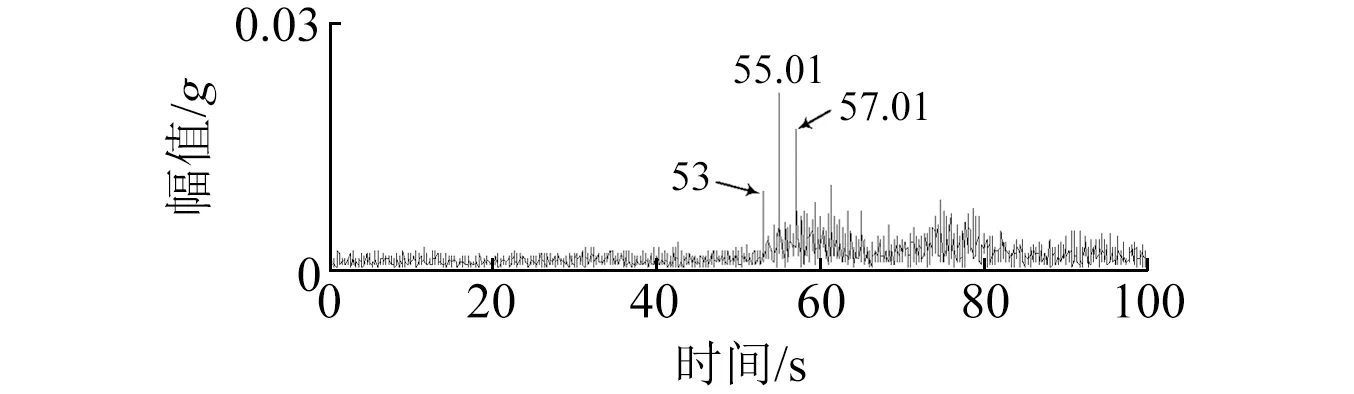
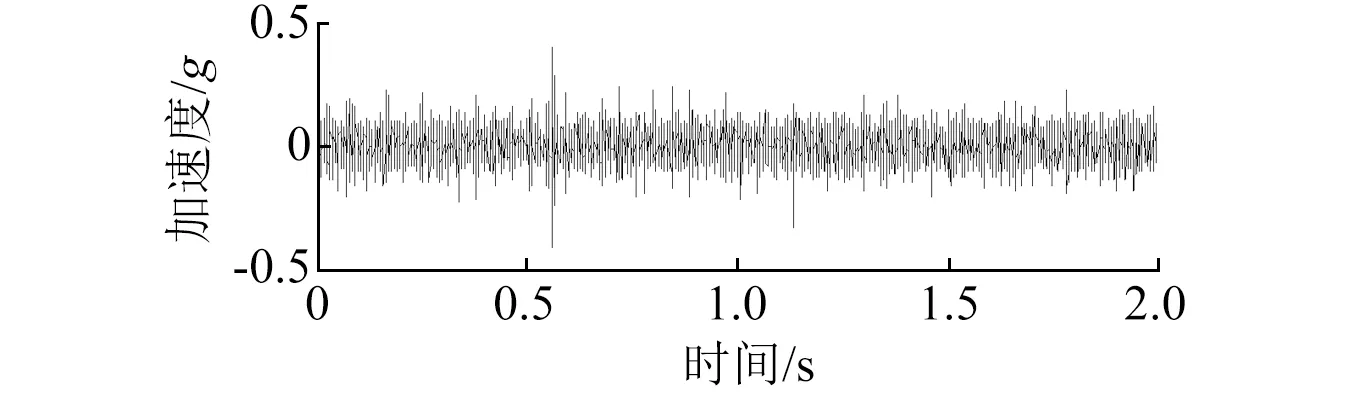
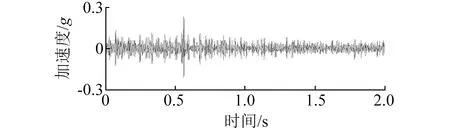
式中：D表示基元函数库；haμbμI(t)为多尺度线调频基元函数；N为分析信号长度；I表示动态分析时间段,I=[kN2-j～(k+1)N2-j]；k为动态时间段的序号，k=0,1,…,2j-1；j表示分析尺度系数，j=0,1,…,log2N-1；KaμbμI为归一化系数，满足‖haμbμI‖=1；aμ和bμ分别表示频率偏置系数和调频率，且满足aμ+2bμt

采用多尺度线性调频基函数对分析信号进行逐段投影，并计算每个时间分析段I内的投影系数和对应的线调频基元函数。当分析信号与多尺度线性调频基函数的相似性越高，其投影系数也就越大，此时，基元函数对应的能量也就越大。因此，需寻求一种动态连接算法∏，使得所连接基元函数对应的信号在整个分析时间内的总能量最大，且连接算法∏应覆盖整个分析时间段，不重叠，即

(2)

此时，对应的投影系数集合和基元函数集合分别为

(3)

CPP方法中连接算法∏的连接步骤如下：

(1) 初始化。以i表示分析时间段序号，Edi表示第i个分析时间段之前分解信号的总能量，li表示连接到第i个分析时间段的前一分析时间段序号，Eei表示第i个分析时间段投影系数对应的分解信号的能量。初始化时,Edi=0,li=0；

(2) 对于动态分析时间段集合I={I1,I2,…}中的每一个元素Ii，查找出与其相邻的所有下一个动态分析时间段集合{Ij}, 如果

Edi+Eei>Edj

(4)

则有

(5)

连接算法∏可保证在整个分析时间段内基元函数组合所对应的信号与分析信号最为相似。基元函数在动态分析时间支持区Ii内的瞬时频率fIi(t)=aμ+2bμt,ti∈Ii，将所有动态时间段集合I={I1,I2,…}中所对应的频率曲线集合fI={fI1,fI2,…}按时间先后顺序连接成线则为信号在整个分析时间段内的瞬时频率估计。

2 S变换

S变换是Stockwell等在研究地球物理数据时提出的一种非平稳信号分析方法。S变换可以认为是一种加高斯窗、且窗宽与信号频率成反比的特殊STFT。S变换在信号低频段具有较高的频率分辨率，而在高频段具有较高的时间分辨率，因此，S变换具有多分辨特性，克服了STFT分辨率固定的缺点。并且，S变换也可认为是一种经过相位修正的连续小波变换(Continuous wavelet transform，CWT)，即S变换保持了原始信号的绝对相位信息，弥补了CWT缺乏相位信息的不足。

对于给定信号，其S变换与S逆变换分别为

(6)

(7)

S变换是一种线性变化，满足线性叠加原理，相对于二次型时频分布(如Wigner-Ville分布，Choi-Williams分布等)，不存在交叉项的干扰，即对于信号x(t)=x1(t)+x2(t)，其S变换满足

S[x(t)]=S[x1(t)]+S[x2(t)]

(8)

为了便于S变换的离散化计算，将其写成关于频域信号X(f)的表达式，即

(9)

式中：X(f)为x(t)的傅里叶变换。由此可得到S变换的离散化计算公式为

(10)

式中：T为采样间隔;N为采样点数，j,n=0,1,…,N-1。

离散S逆变换为

(11)

式中：k=0,1,…,N-1。

3 变转速齿轮故障特征提取步骤

齿轮出现局部故障时，其振动信号中会出现调幅调频信号，对该调幅调频信号的提取与分析对齿轮的故障诊断具有重要意义。而当齿轮处于变转速下运行时，该调幅调频信号具有与转速相关的时变特点，此时，传统的信号滤波方法不再适用。

CPP算法采用分段拟合的思想对信号中频率呈曲线变化的信号成分进行频率估计，可准确估计出变转速下非平稳信号的频率曲线；而S变换是一种线性时频分析方法，不存在交叉项，且保留了信号的绝对相位信息。因此，针对频率大范围变化的调频调幅信号的提取，本文将CPP方法与S变换相结合，提出了基于CPP与S变换的自适应时频滤波方法，并将其用于变转速下的齿轮故障特征提取。本文方法具体计算步骤如下：

H(t,f)={H(ti,f),i=1,2,…,N}

(12)

式中：fωi为ti时刻的半带宽。

(3) 然后采用自适应时频滤波器H(t,f)对信号的时频分布S(τ,f)进行时频滤波，得到滤波后的时频分布S′(τ,f)=S(τ,f)×H(t,f)；

(4) 将时频滤波结果S′(τ,f)进行S逆变换，即可得到提纯后的齿轮故障振动信号S′；

4 算法仿真

为验证本文方法的有效性，设置一调幅调频信号sig1(如式(13))来模拟变转速下的齿轮局部故障，模拟齿数为26，齿轮啮合频率被1倍转频调制，齿轮局部故障信号如图1。为模拟强噪声的干扰，在信号中加入强度为-2 dB的高斯白噪声，得到的仿真合成信号如图2。图2中，齿轮局部故障信号已被完全淹没。

sig1=(1+cos(2π×(25t+sin(3πt))))×cos(2π×26×(25t+sin(3πt)))

(13)

S=sig1+SN

(14)

图1 仿真变转速齿轮故障信号Fig.1 Simulation signal of a faulted gear under variable rotational speed

图2 仿真合成信号Fig.2 Simulation composite signal

图3 估计的啮合频率与实际啮合频率对比Fig.3 Comparison of estimated and actual gear mesh frequency

图4 仿真信号的自适应时频滤波器Fig.4 Adaptive time-frequency filter of simulated signal

采用图4中的自适应时频滤波器对信号进行滤波，滤取的齿轮故障振动信号如图5(a)所示。图5(b)为图5(a)在时间段0.19～0.22 s的局部放大图，图中，滤取的信号与原始齿轮故障信号基本重合，仅在幅值上存在部分差异。

图5 自适应时频滤波提取的齿轮故障信号及局部放大信号Fig.5 Extracted signal of a faulted gear and its partly enlarged signal using adaptive time-frequency filter

同时采用EEMD方法对图2所示的合成信号进行分析，得到的第2个IMF如图6(a)。图6(b)为图6(a)在时间段0.19～0.22 s的局部放大图，图中，IMF与原始齿轮故障信号不仅存在幅值上的差异，而且存在相位畸变。

图6 EEMD方法提取的齿轮故障信号及局部放大信号Fig.6 Extracted signal of a faulted gear and its partly enlarged signal using EEMD

对图5(a)和图6(a)所示信号分别进行阶次谱分析，得到的阶次谱如图7所示，其中，图7(a)为自适应时频滤波信号的阶次谱，图7(b)为IMF2的阶次谱。对比图7(a)和7(b)，虽然两图中在阶次25.04、26.09和27.04处均出现了峰值，表明齿轮啮合频率旁边出现了1倍转频调制现象，但图7(a)中的噪声明显要低，且幅值特性也明显要好。

图7 阶次谱对比Fig.7 Comparison of order spectrum

5 应用实例

为检验本文方法在实测齿轮箱振动信号中提取变转速下齿轮故障特征的有效性，在齿轮箱上进行试验，并采用断齿齿轮和正常齿轮进行对比分析。试验齿轮为正齿轮，主动轴与从动轴的齿数比为55∶75，断齿故障设置为主动轴上，整体切割一个齿以模拟齿轮断齿故障，如图8所示。

图8 断齿齿轮Fig.8 A broken gear

为减少传递路径的影响，将PCB振动加速度传感器直接置于主动轴的轴承座上。试验时，齿轮箱处于空载状态。试验采用LMS数据采集仪同步采集振动加速度信号和主动轴转速信号，采样频率为8 192 Hz。图9为变转速下拾取的齿轮断齿故障的振动信号，信号中出现了较多的冲击成分。

图9 变转速下齿轮断齿故障的齿轮箱振动信号Fig.9 Vibration signal of a gearbox with broken gear under variable rotational speed

采用CPP方法对图9所示信号进行分析，估计出的啮合频率曲线如图10中的虚线所示，图中，频率逐渐增加，表明齿轮箱处于升速阶段。图10中的实线为实测啮合频率曲线(即光电式转速传感器测取的主动轴的转频与齿数的乘积)。图10中，两条曲线基本重合。

图10 估计的啮合频率与实测啮合频率对比Fig.10 Comparison of estimated and measured gear mesh frequency

根据图10中估计的啮合频率曲线(虚线)设计自适应时频滤波器，得到的自适应时频滤波器的时频分布如图11，黑色表示阻带，白色表示通带。图11中可看出，滤波器的中心频率随着信号频率的变化而改变。

图11 断齿齿轮的自适应时频滤波器Fig.11 Adaptive time-frequency filter of a broken gear

采用图11所示的自适应时频滤波器对信号进行滤波分析，滤取的齿轮故障振动信号如图12。图12中存在一定的调制现象，但无法确定故障类型。进一步对滤取的信号(如图12)进行阶次分析，得到的阶次谱如图13。图13中，在阶次53、55.01、57.01处出现明显的峰值，表示齿轮的啮合频率被2倍所转频调制，与齿轮断齿的转频调制现象相符，验证了本文方法提取变转速下齿轮故障特征有效性。

Fig.12 自适应时频滤波提取的齿轮断齿故障信号Fig.12 Extracted signal of a broken gear using adaptive time-frequency filter

图13 断齿齿轮自适应时频滤波振动信号的阶次谱Fig.13 Order spectrum of filtered signal of a broken gear using adaptive time-frequency filter

为增加对比，采用EEMD方法对图9所示信号进行分析，得到的第1个IMF如图14。对IMF1进行阶次分析，得到的阶次谱如图15。图15中，在阶次53、55.01、57.01处也出现了峰值，表明出现了齿轮局部故障，但与图13对比可知，图15中在高频和低频段均存在了较多的噪声，其效果要逊色于图13。

图14 第1个IMFFig.14 IMF1

图15 第1个IMF的阶次谱Fig.15 Order spectrum of IMF1

同时，采用正常齿轮来进行试验，以便进行对比分析。图16为正常齿轮在变转速下采集到的齿轮箱振动信号，图中，信号的幅值较图9要小，且冲击成分较少。

图16 变转速下正常齿轮箱振动信号Fig.16 Vibration signal of a normal gearbox under variable rotational speed

采用本文方法对图16所示正常齿轮箱振动信号进行分析，自适应时频滤波后的信号如图17。对图17所示信号进行阶次谱分析，得到的阶次谱如图18。图18中，在啮合频率阶次55处有一个明显的峰值，但该峰值相对于齿轮断齿故障的幅值要小很多，且啮合频率附近的调制边频带并不明显，即不存在转频调制现象，与正常齿轮的振动特性相符。

图17 正常齿轮箱自适应时频滤波得到的滤波信号Fig.17 Filtered signal of a normal gearbox using adaptive time-frequency filter

图18 正常齿轮箱滤波信号的阶次谱Fig.18 Order spectrum of filtered signal of a normal gearbox

6 结 论

针对变转速下的齿轮故障信号分离与故障特征提取，提出了基于CPP与S变换的自适应时频滤波方法，算法仿真和应用实例验证了本文方法的有效性和优越性。本文主要结论如下：

(1) 自适应时频滤波方法可根据信号的频率变化特点自适应地改变中心频率和带宽，能有效滤取频率呈曲线变化的调幅调频信号，具有较好的信号自适应性，非常适合于变转速下非平稳信号的分析。

(2) 与EEMD方法进行了对比分析，结果表明，自适应时频滤波方法滤取的信号无相位畸变，实现了零相位滤波。

(3) 由于通带内噪声和频域截断的影响，自适应时频滤波方法滤取的信号与原始信号存在一定的幅值误差，因此，如何减少上述两因素对幅值的影响有待进一步改进。

参 考 文 献

[1] 丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术[M].北京：机械工业出版社，2005.

[2] 王平，廖明夫.滚动轴承故障诊断的自适应共振解调技术[J].航空动力学报，2005，20(4): 606-612.

WANG Ping, LIAO Mingfu.Adaptive demodulated resonance technique for the rolling bearing fault diagnosis[J].Journal of Aerospace Power, 2005, 20(4): 606-612.

[3] JENA D P, SAHOO, S, PANIGRAHI S N.Gear fault diagnosis using active noise cancellation and adaptive wavelet transform[J].Measurement, 2014, 47(1): 356-372.

[4] YAN R Q, GAO R X, CHEN X F.Wavelet for fault diagnosis of rotary machines: A review with applications[J].Signal Processing, 2014, 96(5): 1-15.

[5] CHENG Junsheng, YU Dejie, YANG Yu.The application of energy operator demodulation approach based on EMD in machinery fault diagnosis[J].Mechanical Systems and Signal Processing, 2007, 21(2): 668-677.

[6] LEI Yaguo, LIN Jing, HE Zhengjia, et al.A review on empirical mode decomposition in fault diagnosis of rotating machinery[J].Mechanical System and Signal Processing, 2013, 35(1/2): 108-126.

[7] CHENG Junsheng, YANG Yu.A rotating machinery fault diagnosis method based on local mean decomposition[J].Digital Signal Processing, 2012, 22(2): 356-366.

[8] 王衍学，何正嘉，訾艳阳，等.基于LMD的时频分析方法及其机械故障诊断应用研究[J].振动与冲击，2012，31(9): 9-12.

WANG Yanxue, HE Zhengjia, ZI Yanyang, et al.Several key issues of local mean decomposition method used in mechanical fault diagnosis[J].Journal of Vibration and Shock, 2012, 31(9): 9-12.

[9] 彭富强，于德介，刘坚.一种基于多尺度线调频基的稀疏信号分解方法[J].振动工程学报，2010，23(3): 333-338.

PENG Fuqiang, YU Dejie, LIU Jian.Sparse signal decomposition method based on multi-scale chirplet[J].Journal of Vibration and Engineering, 2010, 23(3): 333-338.

[10] 腾伟，安宏文，马志勇，等.基于时频滤波的汽轮机半速涡动故障成分提取[J].振动与冲击，2015，34(3): 178-182.

TENG Wei, AN Hongwen, MA Zhiyong, et al.Semi-speed oil whirl fault component extraction in a stream turbine based on time-frequency filtering[J].Journal of Vibration and Shock, 2015, 34(3): 178-182.

[11] STOCKWELL R G, MANSINHA L, LOWE R P.Localization of the complex spectrum: the S transform[J].IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.

[12] 郭远晶，魏燕定，周晓军，等.S变换时频谱SVD降噪的冲击特征提取方法[J].振动工程学报，2014，27(4): 621-628.

GUO Yuanjing, WEI Yanding, ZHOU Xiaojun, et al.Impact feature extracting method based on S transform time-frequency spectrum denoised by SVD[J].Journal of Vibration and Engineering, 2014, 27(4): 621-628.

[13] 张云强，张培林，李兵.分数阶时频局部二值模式谱在齿轮故障诊断中的应用[J].振动与冲击，2015，34(11): 122-127.

ZHANG Yunqiang, ZHANG Peilin, LI Bing.Application of fractional order time-frequency local binary pattern spectra in gear fault diagnosis[J].Journal of Vibration and Shock, 2015，34(11): 122-127.

[14] 刘建敏，刘远宏，江鹏程，等.基于包络S变换时频图像提取齿轮故障特征[J].振动与冲击，2014，33(1): 165-169.

LIU Jianmin, LIU Yuanhong, JIANG Pengcheng, et al.Extraction of gear fault features based on the envelope and time-frequency image of S transformation[J].Journal of Vibration and Shock, 2014, 33(1): 165-169.

[15] WU Chunyan, LIU Jian, PENG Fuqiang, et al.Gearbox fault diagnosis using adaptive zero phase time-varying filter based on multi-scale chirplet sparse signal decomposition[J].Chinese Journal of Mechanical Engineering, 2013, 26(4): 831-838.

[16] CANDES E J, CHARLTON P R, HELGASON H.Detecting highly oscillatory signals by chirplet path pursuit[J].Applied and Computational Harmonic Analysis, 2008, 24(1): 14-40.

[17] LUO Jiesi, YU Dejie, LIANG Ming.Gear fault detection under time-varying rotating speed via joint application of multiscale chirplet path pursuit and multiscale morphology analysis[J].Structural Health Monitoring, 2012, 11(5): 526-537.

[18] PENG Fuqiang, YU Dejie, LUO Jiesi.Sparse signal decomposition method based on multi-scale chirplet and its application to the fault diagnosis of gearboxes[J].Mechanical System and Signal Processing, 2011, 25(2): 549-557.