动荷载作用下重塑黏质粉土的弹性变形研究

刘干斌，谢琦峰，高京生，郭 华

( 1.宁波大学 岩土工程研究所, 浙江 宁波 315211; 2.宁波市轨道交通集团有限公司, 浙江 宁波 315101 )

在宁波地区，海相沉积软土分布十分广泛，其具有天然含水量高、渗透性差、压缩性大、强度低的特点。而随着宁波市轨道交通的快速建设和投入运营，轨道交通的长期沉降问题也将凸显。实际上，在列车振动荷载作用下，上海地铁1号线运营十余年后某区段累积沉降超过200 mm，轴向差异沉降达到100 mm，严重影响运行安全。针对宁波海相沉积软土地层动力性状的研究，将有助于分析和预测列车荷载作用下轨道交通的沉降和变形稳定。

迄今为止，国内外学者开展了一系列动荷载作用下软土动力特性研究，包括短期强动荷载以及长期弱动荷载的作用，如地震荷载、车辆、轨道交通荷载。一般采用试验与理论研究方法，且主要集中讨论在动荷载作用下孔压与累积塑性应变的发展规律。Seed等[1], Hyde等[2], Guo等[3]进行了一系列的单轴动荷载作用下的动力特性研究；Seed[4]等根据一系列动三轴试验，提出了孔压的发展模式；Wang等[5]根据上万次振动的动三轴试验，提出了通过孔压推求轴向应变的理论公式；刘干斌等[6]通过一系列温控动三轴试验，探讨温度对软土动力特性的影响，并建立了考虑温度影响的应变本构模型；高博等[7]进行了无规律正弦波振动的动三轴试验，研究了粉土在加卸载过程中动模量的变化规律；范思婷等[8]通过一系列温控动三轴试验，研究温度对软土软化特性的影响并建立了软化模型；Sun等[9]通过一系列部分排水条件下的动三轴试验，研究了双向振动对软土轴向应变、体应变的影响，建立了轴向应变的发展模型；王元战等[10]研究了波浪循环荷载作用下软黏土的强度弱化规律，提出了适用于整个动态循环过程的不排水抗剪强度弱化公式。

轨道交通长年运营过程中，由于客运量增加、运行间隔缩短，车辆散热也不断增加，使隧道和车站内热负荷明显变大，造成地下空间温度逐渐升高。纽约交通署公布的数据表明整个地铁系统运行时能够产生足够的热量使得隧道以及站台的温度高于外界温度8～10℃，伦敦地铁隧道内测得的记录很多都超过37℃[11]。王树刚等[12]对北京地铁地下空间温度的实测表明：当隧道内有列车通过时，气温开始波动，靠近站台侧波幅较大，隧道中部温度波幅较小。陈正发等[13]考虑地铁隧道火灾问题，利用自行研制的高温加热试验装置，测定了上海软黏土样在105℃，120℃、150℃和200℃等高温加热2.5 h和4.0 h后的体积变化、干密度和饱和度的变化，测定了105℃、150℃和200℃下恒温4.0 h土的导热情况，结果表明：软黏土在100℃以上高温环境作用下会出现塑性变形和加热硬化现象，并对土的导热系数影响显著。可见，在研究列车荷载作用下土的动力特性时，考虑温度的影响也具有重要的意义。

本文选取宁波地区的黏质粉土，开展不同排水、围压、动应力以及温度条件下饱和重塑黏质粉土的动三轴试验，获得黏质粉土的动力学特性，可以为轨道交通设计和施工提供理论依据。

1 试验概况

选取宁波轨道交通1号线沿线海曙区⑤层黏质粉土，利用温控静动三轴试验仪[14]开展土的动三轴试验。土的天然含水率为29.7%，颗粒比重为2.7，天然孔隙比为0.821，液限为32.6%，塑性指数为8.6。由于粉土黏性较小原状样取样和试验困难。为此，按照土工试验规程制备试验所用重塑样，试样高80 mm，直径39.1 mm，试样粒径配比与原状土一致，其土粒组成：<0.005 mm占13%，0.005～0.075 mm占63%，0.075～0.25 mm占21%，0.25～0.5 mm占3%。

试验时，采用真空饱和法对重塑样进行抽气饱和，当饱和度达到95%，即认为饱和完成。试验过程中，设定4个目标温度，研究温度对黏质粉土动力特性的影响。考虑到温度过高，导致液态水相变，变为气态，试验温度上限设为70℃。采用等压固结σ1=σ3，振动波形为正弦波，经计算列车运行频率为1.11 Hz，试样振动次数为8 000次或直至试样破坏。本次试验主要考虑排水条件、围压、动应力以及温度对黏质粉土的影响，具体试验方案见表1。

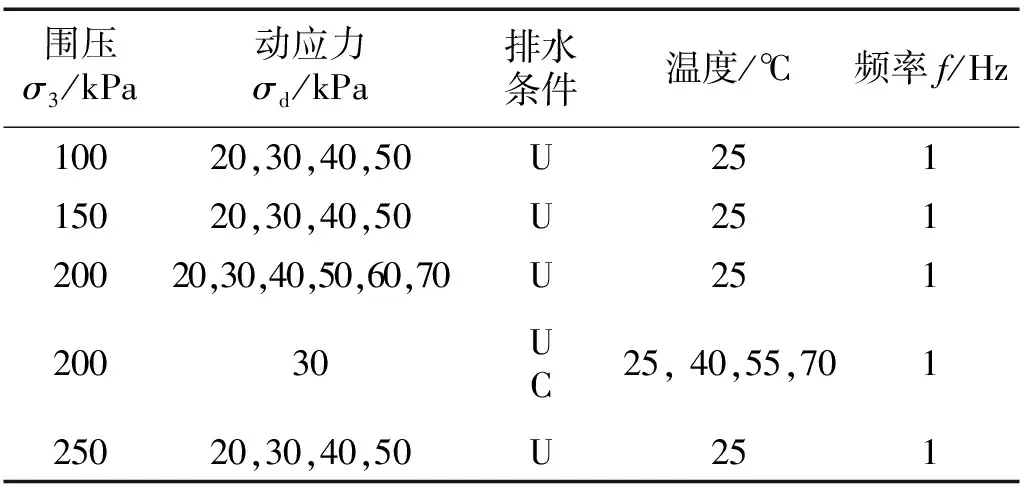
表1 试验方案Tab.1 Test plan

2 试验结果

考虑不同围压σ3、动应力σd、排水条件以及温度对动弹性模量与弹性应变的影响，相关参数的计算公式如下：

(1)

(2)

式中:εd为第N次循环中的弹性应变；εN,max，εN,min分别为第N次循环中最大与最小轴应变；σd为动应力幅值；Ed为第N次循环中的动弹性模量。

2.1 动弹性模量与振动次数关系

根据试验方案(表1)开展不同工况下的动三轴试验，得到饱和重塑黏质粉土试样在不同围压σ3、动应力σd、排水和温度条件下的动弹性模量随振动次数变化曲线，结果如图1所示。

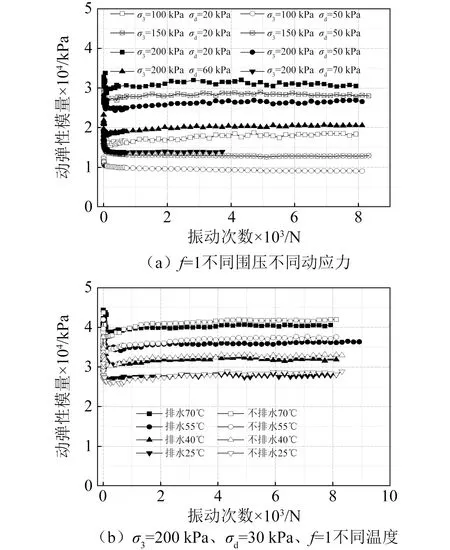
图1 饱和重塑黏质粉土的Ed-N曲线Fig.1 Ep-N curves of saturated remolded clayey soil

由图1可以看出，在相同围压、动应力、排水条件以及温度条件下，动弹性模量在振动初期(100～500次振动)快速衰减至最小值；随着振动次数的增大，动弹性模量有一定的增大，最后趋于稳定。根据Lunne等[15]的研究发现，重塑试样在初始剪切阶段结构性被破坏，抗剪强度逐渐减小；但随着应变的增大，土样再次固结至原位有效应力，其含水率将更低，抗剪强度增大。Lunne等的理论也可用于此处，因为在振动初期，重塑土样累积塑性应变较小，随着振动的进行，土样的结构性发生破坏，使得土样的动弹性模量减小；随着振动次数的继续增加，累积塑性应变增大，土样结构重新排列，且在达到原位有效应力时，动弹性模量增大。

图1(a)为频率f=1、室温(25℃)、不排水条件下，围压和动应力对动弹性模量的影响结果。在振动次数一定，围压相同时，动应力越大，动弹性模量越小。例如围压200 kPa，动应力从20 kPa增大到50 kPa时，动弹性模量减小4.58 MPa，而动应力从50 kPa增加至60 kPa、70 kPa(试样破坏)时，动弹性模量分别减小6.46 MPa和5.23 MPa。由此可见，随着动应力的增大(越接近临界动应力)，其对动弹性模量的影响也会随之增大。

在相同振动次数和动应力下，围压越大，动弹性模量越大。在动应力较小时(σd=20 kPa)，围压为100 kPa、150 kPa、200 kPa时的动弹性模量分别为18.53 MPa、28.01 MPa、31.52 MPa，相同围压增量下的动弹性模量增量逐渐减小。在动应力较大时(σd= 50 kPa)，围压为100 kPa、150 kPa、200 kPa时的动弹性模量分别为9.02 MPa、13.24 MPa、26.34 MPa，相同围压增量下的动弹性模量增量逐渐增大。由此可见，在相同动应力条件下，围压对动弹性模量的影响与动应力大小有关。

图1(b)为在围压σ3=200 kPa，动应力σd=30 kPa，频率f=1 Hz下，不同温度、排水条件对动弹性模量的影响。在不排水条件下，振动次数相同时，温度越高，动弹性模量越大，土体出现热硬化现象；此外，随着温度的升高，动弹性模量的发展趋势有明显的区别，在动弹性模量恢复阶段，温度越高，动弹性模量稳定越快。在25℃时，动弹性模量在振动次数达到4 000次基本达到稳定；而在70℃时，动弹性模量在1 200次左右就已基本稳定。在排水条件下，动弹性模量的发展趋势与不排水条件下一致。在相同振动次数下，温度越高，动弹性模量越大，土体也出现热硬化现象。在其他条件相同，不同排水条件下，试样动弹性模量的发展趋势一致，不同排水条件对动弹性模量的影响可忽略。在一个振动循环内，孔隙水来不及排出，排水引起的应变差为高阶无穷小量，可忽略；此外，在试验应力状态下，固液相可认为是不可压缩的，试样中水土的比值对弹性应变的影响也可不计，即式(2)得到的动弹性模量与是否排水无关。

2.2 弹性应变与振动次数关系

根据试验方案(表1)进行动三轴试验，得到饱和重塑黏质粉土试样在不同围压σ3、动应力σd、排水条件以及温度条件下的弹性应变随振动次数变化曲线，结果如图2所示。在相同围压、动应力条件下，在振动初期(100～500次振动)，弹性应变急剧增大至峰值；经过峰值后，随着振动次数的增大，弹性应变逐渐减小，最后至稳定，振动越快越来不及反应所以应变越小，此规律与动弹性模量的发展规律相反。

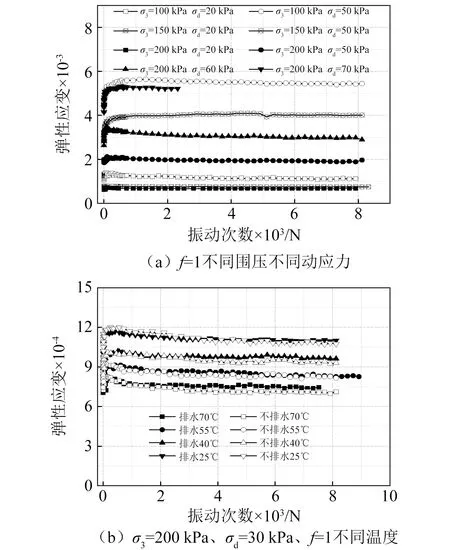
图2 饱和重塑黏质粉土的εd-N曲线Fig.2 εd-N curves of saturated remolded clayey soil

由图2(a)可知，在振动次数和围压相同时，动应力越大，弹性应变越大，例如围压为200 kPa，动应力从20增大到50 kPa时，弹性应变增加0.1259%，而动应力从50 kPa增至60 kPa、70 kPa(试样破坏)时，弹性应变分别增大了0.105%与0.223%。由此可知，随着动应力的增大，动应力对弹性应变的影响也会随之增大。在振动次数一定和相同动应力条件下，围压越大，弹性应变越小。

由图2(b)可知，在不排水、相同振动次数条件下，温度越高，弹性应变越小；此外，随着温度的升高，弹性应变的发展模式与动弹性模量类似，温度越高，弹性应变稳定所需振次越小。在排水条件下，弹性应变的发展趋势与不排水条件下一致。在相同振动次数下，温度越高，弹性应变越小。在不同排水条件下，弹性应变的发展规律基本相同，可忽略不同排水条件对弹性应变的影响。

3 经验公式推导

3.1 动弹性模量～弹性应变经验公式

由图1、图2可知，在经过数千次的振动后，试样的动弹性模量以及弹性应变均已经过峰值或最小值达到稳定值，其值分别记为Ed,stab与εd,stab。选取频率f=1 Hz，室温(25℃)，不排水条件，100 kPa、150 kPa、200 kPa和250 kPa围压、20 kPa、40 kPa、50 kPa、60 kPa和70 kPa动应力条件下的Ed,stab与εd,stab的稳定值，将相应的1/Ed,stab与εd,stab绘于图3 (注：留动应力为30 kPa的数据用于公式验证) 。

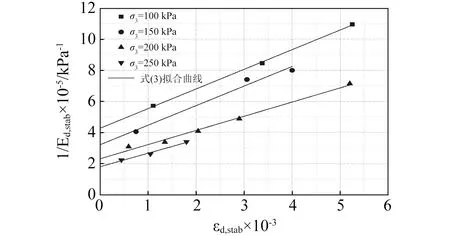
图3 饱和重塑黏质粉土的1/Ed,stab-εd,stabFig.3 1/Ed,stab-εd,stab of saturated remolded clayey soil

为描述同一围压下1/Ed,stab与εd,stab的关系，建立如下经验公式：

1/Ed,stab=kεd,stab+t

(3)

式中：k,t分别为试验参数，由试验确定。其中，参数t的物理意义为在不同围压下，εd,stab趋近于零时，即动应力趋近于零时，试样动弹性模量的倒数，记为1/Ed0,stab。参数k表示Ed,stab随εd,stab的变化快慢，k值越大，Ed,stab衰减越快。

利用式(3)对图3中相同围压下的1/Ed,stab-εd,stab关系点进行拟合，结果见表2。

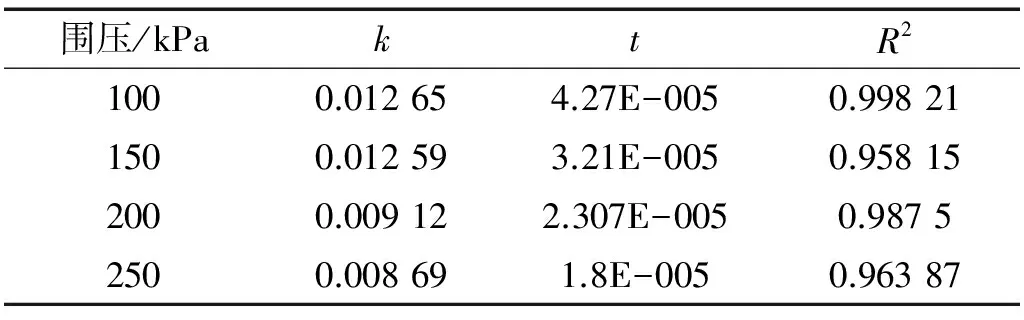
表2 拟合结果Tab.2 The fitting results

由表2可知，公式(3)拟合效果好，能反映不同围压、动应力下，1/Ed,stab-εd,stab的关系。

k值随围压的增大而减小，其拟合结果如下：

k=-3.07×10-5σ3+0.016 14

(4)

式中：R2=0.772。

t值随围压的增大而减小，其拟合结果如下：

(5)

式中：R2=0.972 2。

k，t值的拟合结果如图4(a)、(b)所示。

图4 参数k，t与围压关系及其拟合结果Fig.4 k-σ3, t-σ3 and their fitting curves

由式(4)、式(5)以及图4(a)、(b)可得：k,t拟合较好，将k，t的表达式代入式(3)，得经验公式：

对式(6)两边取倒数得：

(7)

利用式(7)对Ed,stab-εd,stab进行拟合，结果如图5所示，可以看出：经验式(7)拟合较好，可用于计算不同围压下，长期动荷载作用后黏质粉土动弹性模量值。当围压一定，εd,stab趋近于零时，即相当于试样所受动应力极小情况下，长期动荷载作用下的动弹性模量大小。

图5 饱和重塑黏质粉土的Ed,stab-εd,stab及其拟合曲线Fig.5 Ed,stab-εd,staband fitting curves of saturated remolded clayey soil

3.2 动弹性模量计算经验公式

由参数t的物理意义可得：

t=1/Ed0,stab

(8)

将式(8)代入式(3)得：

1/Ed,stab=kεd,stab+1/Ed0,stab

(9)

由线性方程的特点可知，可通过已知点推求任一未知点。若已知在同一围压下，动应力σd1长期动荷载作用后产生的动弹性模量与弹性应变分别为Ed1,stab与εd1,stab，则可推求在另一动应力σd2长期动荷载作用后产生的动弹性模量Ed2,stab与弹性应变εd2,stab得：

1/Ed2,stab=k(εd2,stab-εd1,stab)+1/Ed1,stab

(10)

动弹性模量与弹性应变的定义式(2)得：

(11)

将式(11)代入式(10)，两边同乘动应力σd2得：

(12)

合并同类项得：

(13)

将式(4)代入式(13)得：

通过不同围压下，动应力σd=20 kPa时的动弹性模量，利用式(14)，计算不同围压，动应力σd=30 kPa下动弹性模量大小。将动弹性模量计算值与实测值对比，列于表3。

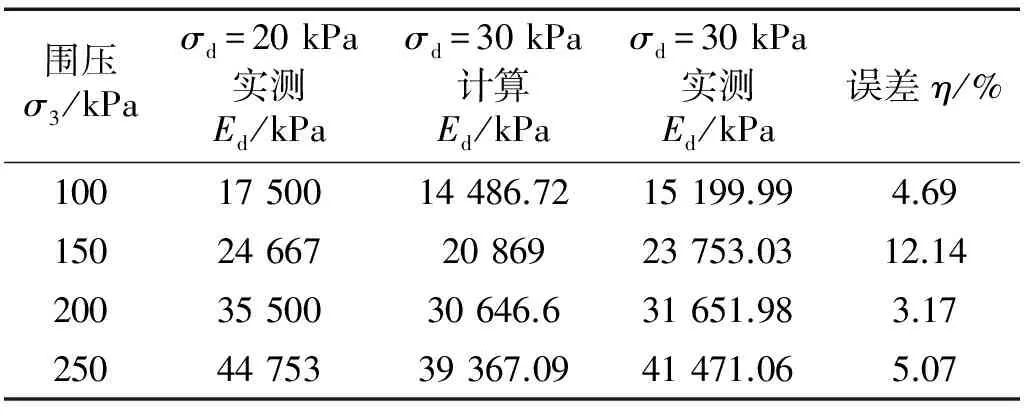
表3 Ed计算值与实测值对比Tab.3 The comparison of calculated and measured values of Ed

由表3可知，在动应力为30 kPa时，不同围压下的动弹性模量计算值与实测值的误差在可接受范围内，式(14)能用于动弹性模量的预测。

3.3 弹性应变计算经验公式

将式(2)代入式(13)得：

(15)

将式(4)代入式(15)得：

(16)

利用不同围压、动应力σd=20 kPa时的弹性应变结果，并利用式(16)，可以计算不同围压，动应力σd=30 kPa时的弹性应变。弹性应变计算值与实测值的对比结果如表4所示。由表4可知，在动应力为30 kPa时，不同围压下的弹性应变计算值与实测值的误差在可接受范围内，式(16)能用于弹性应变的预测。

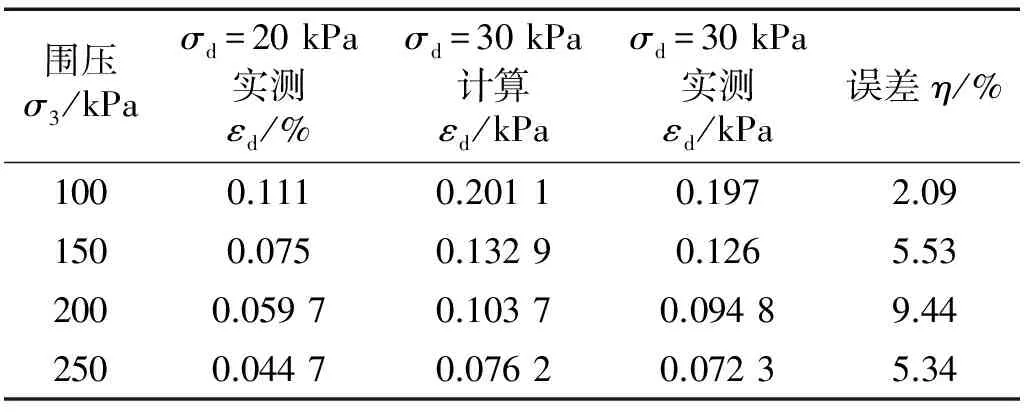
表4 εd计算值与实测值对比Tab.4 The comparison of calculated and measured values of εd

4 结 语

通过开展宁波重塑黏质粉土的动三轴试验，研究了围压、动应力、排水条件以及温度等因素对土动力特性的影响，主要结论如下：

(1) 重塑黏质粉土的动弹性模量和弹性应变随振动次数的发展规律相较于一般重塑软土有较大不同。在长期动荷载作用下，重塑黏质粉土的Ed-N与εd-N曲线存在明显的极值点，极值点后Ed与εd逐渐恢复至稳定。

(2)在长期动荷载作用下，温度越高，重塑黏质粉土动弹性模量值越大，弹性应变越小，出现热硬化现象。

(3) 建立的考虑围压影响的动弹性模量～弹性应变经验公式以及动弹性模量和弹性应变计算公式可用于长期动荷载作用下黏质粉土的动弹性模量和弹性应变计算。

参 考 文 献

[1] SEED H B, CHAN C K, MONISMITH C L.Effects of repeated loading on the strengthand deformation of compacted clay[J].Highway Research Board Proceedings, 1955, 34: 541-558.

[2] HYDE A F L, BROWN S F.The plastic deformation of a silty clay under creep andrepeated loading[J].Geotechnique 1976, 26(1): 173-84.

[3] GUO L, WANG J, CAI Y Q, et al.Undrained deformationbehavior of saturated soft clay under long-term cyclic loading[J].Soil.Dyn.Earthq.Eng., 2013, 50:28-37.

[4] SEED H B, MARTIN P P, LYSMER J.Pore-water pressure changes during soil liquefaction[J].Journal of Geotechnical and Geoenvironmental Engineering, 1976, 102:12074.

[5] WANG J, GUO L, CAI Y Q, et al.Strain and pore pressure development onsoft marine clay in triaxial tests with a large number of cycles[J].Ocean.Eng.,2013,74:125-32.

[6] 刘干斌, 范思婷, 陈斌, 等.考虑温度影响的饱和软黏土累积变形特性研究[J].岩土工程学报, 2016, 38(7): 1238-1245.

LIU Ganbin, FAN Siting, CHEN Bin, et al.Characteristics of cumulative deformation of saturated soft clay considering temperature effect[J].Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1238-1245.

[7] 高博,张鸿儒.邯郸与太原两地粉土动力特性的试验研究[J].工程地质学报, 2008, l6(4): 502-506.

GAO Bo, ZHANG Hongru.Cyclical tri-axial tests for dynamic modulus characteristics of silty soils at six sites in Handan and Taiyuan[J].Journal of Engineering Geology, 2008, 16(4): 502-506.

[8] 范思婷, 刘干斌, 陈斌, 等.考虑温度影响的饱和软黏土应变软化研究[J].振动与冲击, 2017, 36(6): 1-6.

FAN Siting, LIU Ganbin, CHEN Bin, et al.Study on strain softening of saturated soft clay considering temperature effect[J].Journal of Vibration and Shock, 2017, 36(6): 1-6.

[9] SUN L, GU C, WANG P.Effects of cyclic confining pressure on the deformation characteristics of natural soft clay[J].Soil Dynamics and Earthquake Engineering, 2015, 78: 99-109.

[10] 王元战, 杨攀博, 孙熙平, 等.循环荷载下软黏土强度弱化研究及其动力计算应用[J].岩土工程学报, 2015, 37(5): 821-828.

WANG Yuanzhan, YANG Panbo, SUN Xiping, et al.Strength weakening of soft clay under cyclic loading and its dynamic calculation[J].Chinese Journal of Geotechnical Engineering, 2015, 37(5): 821-828.

[11] 王树刚, 王如竹, 朱颖心.北京地铁地下空间温度的测量与分析[J].地下空间, 2002, 22(4): 339-343.

WANG Shugang, WANG Yuzhu, ZHU Yingxin.Measurement and analysis of temperature in underground space of beijing subway[J].Underground Space, 2002, 22(4): 339-343.

[12] 胡增辉, 李晓昭, 赵晓豹,等.隧道围岩温度场分布的数值分析及预测[J].地下空间与工程学报, 2009, 5(5): 867-872.

HU Zenghui, LI Xiaozhao, ZHAO Xiaobao, et al.Analysis and prediction of the temperature distribution around tunnels[J].Chinese Journal of Underground Space and Engineering , 2009, 5(5): 867-872.

[13] 陈正发,朱合华,闫治国，等.高温后上海软黏土的物理性能试验研究[J].岩土工程学报, 2015, 37(5): 924-931.

CHEN Zhengfa, ZHU Hehua, YAN Zhiguo, et al.Experimental study on physical properties of Shanghai soft clay under high temperatures[J].Chinese Journal of Geotechnical Engineering, 2015, 37(5): 924-931.

[14] 刘干斌, 范思婷, 叶俊能, 等.温控动三轴试验装置的研制及应用[J].岩石力学与工程学报, 2015,34(7):1345-1352.

LIU Ganbin, FAN Siting, YE Junneng, et al.Development and application of a temperature-controlled dynamic triaxial test system [J].Chinese Journal of Rock Mechanics and Engineering, 2015,34(7):1345-1352.

[15] LUNNE T, BERRE T, ANDERSEN K H, et al.Effects of sample disturbance and consolidation procedures on measured shear strength of soft marine Norwegian clays[J].Canadian Geotechnical Journal, 2006, 43(7): 726-750.