基于环境噪声的浅海海底单参数反演

陈 勃，赵 梅，胡长青

(1. 中国科学院大学，北京100049；2. 中国科学院声学研究所东海研究站，上海201815)

0 引 言

环境噪声作为海洋中的背景声场，无时无刻不存在于海洋环境中，环境噪声在传播过程中，不断与海底海面发生接触，携带有大量的海底信息，因此，利用环境噪声去反演海底信息成为了可能。Cox[1]在上世纪70年代开始对海洋环境噪声相关性进行研究，推导了噪声场中相关性的理论表达式并与实验数据吻合较好；Kuperman和Ingeito[2]利用波动理论建立了海洋环境噪声场模型，即 KI模型，假设噪声源为随机均匀分布在海面以下无限大平面上的单极子源，同时考虑了连续谱和离散谱的贡献，可以相当准确地描述噪声场性质，但计算速度较慢；Buckingham[3]利用简正波模型，忽略近场连续谱的贡献，得到了噪声场模型的数学表达式；Harrison[4-5]利用射线方法，将声速剖面、噪声源深度等海洋环境中的多种影响作为输入参数，建立了噪声场的射线模型，该模型计算速度快，但缺乏大量实验数据的验证；T.C.Yang等[6]对Buckingham的方法进行了改进，在大掠射角处采用波束积分的方法进行计算，提高了模型的精度；Siderius等[7-8]利用垂直阵列得到噪声场竖直方向上的相关信息，并由此反演海底的分层情况，并通过大量实验数据对反演结果进行了验证。

传统的噪声场建模方法，需要确切的海底信息作为输入参数，这些海底信息包括海底的声速、密度、衰减系数等，若考虑分层海底的情况，还需输入各层海底厚度及各层对应的声学参数，这些参数获取困难，同时也使得模型变得复杂，若使用匹配场技术进行海底反演，过多的待反演参数也会使传统的优化算法难以收敛到全局最优解。本文将一种简化的海底反射模型运用到噪声场建模中，以单参数FdB[9-10]描述海底反射损失，该参数对于不同类型的海底敏感，可用于快速海底底质分类研究。基于单参数的噪声场模型，不仅可以简化反演过程，做到快速反演，同时由于模型将多个海底声学参数简化为一个单参数FdB，也在一定程度上规避了海底多参数之间的耦合及敏感性问题。本文首先计算得到了基于单参数的噪声场模型空间相干系数表达式，随后通过仿真和实验数据开展了基于环境噪声的浅海海底单参数反演研究。

1 理论计算

1.1 单参数浅海海底模型

本文中假设海底为一液态半无限大海底，这一海底模型，也称作瑞利模型。瑞利模型通过海底声速、密度和衰减系数三个参数来描述一个均匀且存在吸收的半无限海底。这种模型虽然简单，但却在浅海传播问题上有很好的适用性，适用于大范围快速的海底反演。图1给出了三种典型沉积物下反射损失的计算结果，可以看到，在小掠射角区域，即临界角以下，反射损失与掠射角之间近似于线性关系，而大于掠射角之后，反射损失骤增并逐渐趋近于一个常数。在考虑浅海传播问题时，声在传播过程中会与海底有多次接触，大掠射角区域因为传播损失过大，在多次反射后对于声场的影响就可以忽略，因此在一定距离后对于声场起主要贡献的为小掠射角下的声波。

图1 三种不同底质的海底反射损失Fig.1 Seabed reflection losses of three different types of sediments

在液态半无限大海底的假设下，声波入射到海底的反射系数可以通过海底声速、密度以及衰减系数表示：

其中，Z和Zw分别代表海底和海水的声阻抗。小掠射角下，海水中的声阻抗表示为

其中：ρw为海水密度；cw为海水声速；βw为海水的损耗因子；θ代表掠射角，即声波入射方向与海底的夹角。声波在海水中的衰减通过为声速添加一虚部的形式体现，在浅海、低频这两个前提下，海底声吸收要比海水中大得多，因此往往可以忽略βw的影响。同理，海底的声阻抗表示为

根据Hamilton的假设，海底密度ρ和海底中声速c均不随频率变化，β是海底的损耗因子，cscθ为掠射角的余割函数。损耗因子与声衰减系数α(dB/λ)的关系为

海底反射损失BL写作：

将公式(1)、(2)、(3)代入式(5)得：

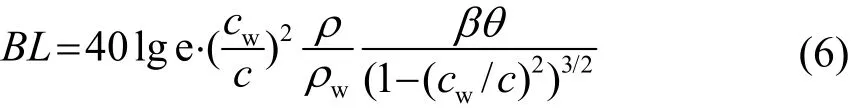
由于小掠射角下反射损失随掠射角的增加近似呈线性增长，定义单参数FdB为海底反射损失随掠射角的变化率，认为它是一个常数，则海底反射损失BL可以表示为

联立公式(6)和公式(7)，可以得到单参数FdB的表达式

将反射能量损失写成指数形式，即

单参数的分贝形式和指数形式F之间的换算关系式为

至此，我们得到了单参数的表达式。该参数与海底的声速、密度以及衰减系数有关，可以看作小掠射角下反射损失曲线的斜率。单参数海底模型是对传统海底模型的一种简化，利用这一海底模型进行反演可以提高反演效率，但需要指出的是，由于在单参数推导过程中没有考虑切变波的影响，在处理非常“硬”的海底时，切变波引起的反射损失影响增大，此时模型误差会增大。基于单参数进行海底反演的方法在文献[9]和文献[10]中有涉及，反演取得了较好的效果。

1.2 浅海环境噪声场空间相干系数表示

本文中考虑的噪声来源主要为风成噪声，风成噪声顾名思义由海面风作用产生，当风吹过海面时，海面形成无数个随机分布的海浪，海浪落下破碎形成的声音即为风成噪声。假设这些噪声源之间相互独立，位于一个海平面以下且靠近海平面的无限大平面上，如图2所示。浅海环境由海水层和海底构成，噪声源位于海平面以下z'处。

图2 海面噪声源分布示意图Fig.2 Noise source distribution on the sea surface

噪声场的空间分布特征用点的声场与点声场的互谱密度S12表示，当两个声场的声源在同一位置时，简化为局部的声场强度。这种利用互谱密度表示的噪声场的空间特性，可以通过水听器阵测量出来，这为随后的反演提供了基础。若把海面看作一个极坐标系，用r、φ表示，那么互谱密度写作：

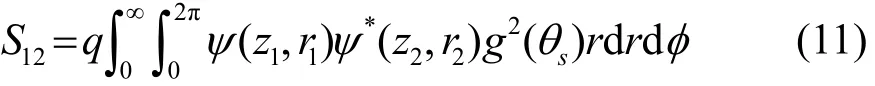
式中：q代表单位面积的噪声源强度为噪声源的指向性；θs为出射角。由于噪声源靠近海表面，且海表面看作是一软边界，因此，噪声源指向性一般认为与偶极子指向性相同，即代表第n处接收点的声压，结合射线理论，式(11)进一步写作：

式中，θr和θb分别代表接收角和海底反射角；Sc和Sp分别代表完成一次声循环的距离和声源不经海底反射到达接收点的声传播距离；Vb代表海底反射系数。两个水听器接收到的噪声信号是存在相位差的，这一相位差写做代表相邻接收水听器之间的距离。结合图3的几何关系，相位差表示为

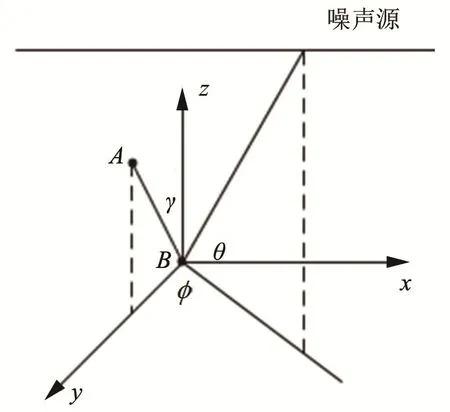
图3 水听器A、B几何分布示意图Fig.3 Geometric distribution of hydrophone A and B

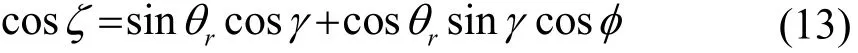
将式(13)代入式(12)，进一步化简，得到：

结合公式(9)，用单参数的形式表示海底反射系数，并且对公式(14)进行归一化处理，得到最终的噪声场空间相干系数表达式为

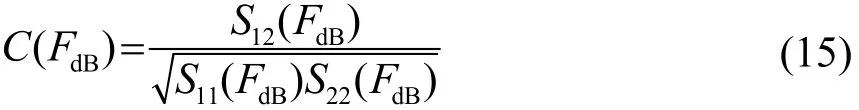
结合上述推导，得到了单参数模型下，噪声场的空间相干系数的计算方法。

2 数值仿真

仿真采用 100 m深的 Pekeris波导，声速为1500 m.s-1，下方海底看作一无限大液态半空间，其中的声速为1800 m.s-1，密度为1.80g.cm-3，衰减系数为 0.5 dB.λ-1，一对接收水听器位于水下50 m处，计算频率为500 Hz。在本节中利用传统模型与单参数模型下计算得到的噪声场垂直相关性进行对比。其中传统的计算模型采用Harrison的射线模型，利用射线理论得到噪声源和接收点间的格林函数，并同样利用互谱密度来表示噪声场中两点间的空间相干系数。计算结果如图4中的实线所示，图4中的圆圈线代表单参数模型下的计算结果。其中横坐标Ω为一无量纲数，表示为由图4可以看出，两种方法下得到的空间相干系数的变化规律一致，由此验证了本文采用的单参数方法计算噪声场空间相干系数的准确性。

2.1 与传统模型对比

图4 传统模型下和单参数模型下浅海环境噪声场空间相干系数比较Fig.4 Comparison of ambient noise field correlation between traditional model and single parameter model

2.2 敏感性分析

不同的海底沉积类型可以通过其物理属性进行判定，其中中值粒径[11]是最为常用的参数之一。利用中值粒径进行分类最具代表性的标准是 Shepard的砂-粉砂-黏土分类。Hamilton[12]根据Shepard的分类方法，结合大量的实验数据，得到了大陆台地海洋环境下海底声速和密度与中值粒径Mz的经验公式：

式(16)、(17)中，ρ和c分别代表海底的密度和声速，中值粒径Mz可以有效反映海底沉积物的平均粒度值，单位：为粒子的直径(mm)。通过中值粒径可以区分海底沉积物的类型，对海底进行分类。将式(16)和式(17)代入式(8)中，若把海水中的声速和密度看作固定常数，此时便可以将单参数写成中值粒径Mz和衰减系数α的函数。图5中的四条曲线代表了衰减系数(dB/λ)分别为 0.2(虚点混合)、0.4(点线)、0.6(虚线)和 0.8(实线)时，单参数随中值粒径Mz的变化规律。不同的中值粒径代表了不同的海底沉积类型，随着中值粒径的增大，单参数呈近似指数规律上升，说明单参数对于不同的海底类型是敏感的，通过反演海底单参数去探究海底特性并进行底质分类工作是可行的，同时单参数与衰减系数之间也存在正比关系。值得指出的是，在实际海底沉积情况下，中值粒度与衰减系数之间也存在一定的耦合关系，衰减系数通常通过下式计算得到：

其中：f是声音频率；K是衰减因子，与海底类型有关；m是近似线性关系的指数，具体大小存在争议，一般认为在0.9～1.1之间。

图5 单参数FdB随中值粒径Mz以及衰减系数α 的变化规律Fig.5 The variations of the single parameter FdB with median particle size Mz and attenuation coefficient α

图6 三种不同底质下单参数噪声场空间相干系数模型计算结果Fig.6 Calculation results of the spatial correlation coefficient of ambient noise field for three different sediments

图6为三种不同底质类型下单参数模型计算得到的噪声场空间相干系数。黏土质粉砂是最软的，因此其密度是最小，声波在其中的传播也最慢；粉质黏土的孔隙率比较大，声波在入射到这种底质上时，大部分穿透到海底，因此声波损失较多。这种影响体现在图6中，相干系数曲线振幅大，下降迅速；细砂型海底则与粉质黏土正好相反，在细砂型海底中，声速和密度都非常大，孔隙率很低，这种海底的反射系数较大，声波不容易透射，大部分入射的声波都反射回水体中，体现在相干系数曲线上为振幅相对较小，且下降缓慢；介于粗砂型海底和粉质黏土海底之间的是砂质粉砂型海底，它的声速、密度及孔隙率均处于中等水平，相干系数曲线的下降速度也处于中间，但可以明显区别于其他两种类型。从图6中不同单参数下的空间相干系数也再次印证了单参数对于不同的底质类型是敏感的。

3 实验研究

噪声场空间相干系数是浅海噪声场中相对稳定的物理量，其受海况变化影响较小，主要由海底特性决定。因此，可以利用噪声场的空间相干系数来反演浅海海底特性。本文利用噪声场数据来反演实验海域的海底单参数，并确定海底沉积物的类型。

3.1 实验介绍

实验数据来自于某浅海海域环境噪声试验。实验期间海面风速为8～10 m.s-1，浪高1～2 m，海面可见白浪花，实验时间选在禁渔期，周围基本没有船只，因此噪声来源主要为风成噪声。实验海域海深 70 m，地势较为平坦，声速剖面由温盐深仪(Conductance Temperature Depth，CTD)测得，如图7所示，剖面为典型的夏季浅海声速剖面，在25～35 m之间存在明显温跃层。实验采用8元水听器阵，各阵元之间间距 0.5 m，全阵位于温跃层以下，阵中心在 45 m 深处，接收器工作频带为 20 Hz～20 kHz，内置20 dB前置放大器。由于受海流的作用，水听器阵列在水下会发生倾斜，实验时在阵列的上、中、下三个位置处分别固定一个温深仪(Temperature and Depth，TD)，用来计算阵列的倾斜角度。

图7 实验海域声速剖面Fig.7 Sound speed profile in experimental sea area

3.2 反演海底单参数

待反演参数为海底单参数FdB，代价函数 (Cost Function，CF)定义为实验中水听器间相干系数与理论计算得到的水听器间相干系数的均方差，表示为

在第1节的理论推导中，空间相干系数可以通过单参数FdB唯一表示，因此在式(19)中，Cf也可以通过单参数FdB来表示。实验数据选取 100～1800 Hz频段内的环境噪声数据进行计算，相干系数通过水听器接收的噪声信号计算得到，取连续若干段相同长度的噪声信号，分别计算空间相干系数，然后取平均值，即得到这段时间内的噪声场空间相干系数。实验选取的一对水听器间隔为1 m，但该间距并不能当作垂直间距进行计算，因为实验时阵列发生倾斜，水听器连线与垂直方向存在夹角。将多次反演结果平均，得到单参数FdB的值为3.3。图8为代价函数随单参数的变化。

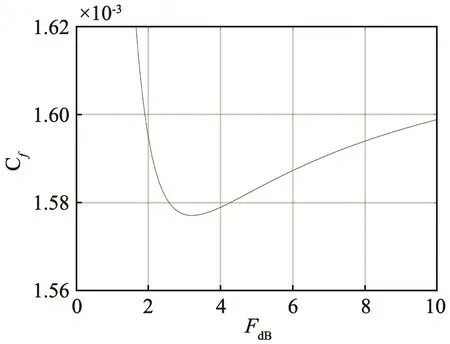
图8 代价函数随单参数的变化情况Fig.8 The variation of cost function with the single parameter FdB

图9是反演曲线与实验曲线的对比情况，由图9可以看到实验曲线与反演曲线拟合较好，具有近似相同的过零点以及最低点。

图9 反演曲线和实验曲线的对比Fig.9 Comparison between inversion curve (solid line) and experimental curve (dashed line)

3.3 海底底质分类及反演结果验证

单参数虽然对于不同底质类型是敏感的，但是直接利用单参数FdB的值确定海底类型却存在问题，表1给出了300 Hz下，8种高声速海底[13]对应的中值粒径、衰减系数以及单参数的值。由表1可以看到，随着中值粒径的增长，单参数的值并不呈线性变化，这主要是因为在中值粒径达到某一值后，随着中值粒径的增大，衰减系数开始单调递减，从而影响了单参数值的变化。

表1 8种不同底质类型对应的基本参数Table 1 Basic parameters of eight types of sediments

因此，若利用单参数去确定底质类型，还需借助其他参数值。在这里选取了海底反射临界角θc，由于大掠射角处噪声损失很快，对于噪声场空间相干性的贡献很小，因此在这里把大掠射角处的海底反射损失置为 1，即忽略大掠射角处噪声对于相干性的影响，那么式(7)重写为

这样噪声场空间相干系数即表示为单参数FdB和临界角θc的函数C(FdB,θc) ，又由于斯奈尔定律：

因此，空间相干系数进一步写做的形式。同样利用噪声场相干系数的实验值与理论值的均方差函数作为代价函数再一次反演海底单参数FdB和海底声速c2，图10是反演结果的一维和二维后验概率密度，图10中左图为单参数FdB一维后验概率密度，搜索区间为1到10，下图为海底声速c2的后验概率密度，搜索空间为1500～2500 m.s-1，假设两个参数在先验空间中满足均匀分布，对多次反演结果进行平均，最优值为FdB= 3 .35，c2=1679 m.s-1。从图10中可以看到单参数FdB的后验概率收敛情况较好，能够收敛到全局最优解处，而声速c2的后验概率曲线较为平坦，原因在于单参数FdB和声速c2之间存在一定程度的参数耦合，当声速c2增加或者减小时，单参数FdB也会发生变化，参数耦合会增大反演结果的不确定性，导致声速c2的一维后验概率密度收敛情况不好。

图10 单参数和海底声速的一维和二维后验概率密度Fig.10 One and two dimensional posteriori probability densities of the single parameter FdB and seabed velocity

将c2=1679 m.s-1代入式(17)，得到实验海域海底沉积物的中值粒径为 3.9，海底沉积物类型接近粉砂质砂，根据文献[14]记录，该处海域沉积物中值粒径在4左右，沉积物类型为粉砂质砂，本文的反演结果与实际情况符合较好。

4 结 论

利用环境噪声反演浅海海底特性是一种被动探测手段，可以有效节约调查时间和成本，但是建立在多维海底模型上的反演方法，往往复杂性高，反演时间长。根据反演复杂性随着反演参数的个数减少而降低的原理，本文提出了一种建立在单个参数海底模型基础上的噪声场空间相干系数计算方法，有效地降低了反演的复杂性。为了验证该方法的可行性，本文通过仿真计算对比了空间相干系数在单参数模型下和传统模型下的计算结果，两者拟合较好。

另外，进一步观察单参数模型下噪声场的空间相干系数对于不同的海底类型的敏感性。结合某海试数据对实验海域的海底单参数进行了反演，该处海域单参数值为FdB=3.35，结合海底反射临界角，进一步得到了该处海域的海底沉积物类型为粉砂质砂，与实际情况符合较好。该方法对于高声速海底类型的快速反演较为有效，但当海底沉积层较薄，基底对于反射损失影响较大时，单参数方法的适用性还有待进一步验证。

参考文献

[1] COX H. Spatical correlation in arbitrary noise field with application to ambient noise[J]. J. Acoust. Soc. Am., 1973, 54(5): 1289-1301.

[2] KUPERMAN W A, INGENITO F. Spatial correlation of surface generated noise in a stratified ocean[J]. J. Acoust. Soc. Am., 1980,67(6): 1988-1996.

[3] BUCKINGHAM M J. A theoretical model of ambient noise in a low-loss, shallow water channel[J]. J. Acoust. Soc. Am., 1980,67(4): 1186-1192.

[4] HARRISON. C. H. Formulas for ambient noise level and coherence[J]. J. Acoust. Soc. Am., 1996, 99(4):2055-2066.

[5] HARRISON C. H. CANARY:A model of ambient noise, coherence and array response[J]. Applied Acoustics, 1997, 51(3):289-315.

[6] YANG T C, KWANG Y. Modeling the environmental influence on the vertical directionality of ambient noise in shallow water[J].J. Acoust. Soc. Am., 1997, 101(5): 2541-2554.

[7] SIDERIUS M, HARRISON C H, PORTER M B. A passive fathometer technique for imaging seabed layering using ambient noise[J]. J. Acoust. Soc. Am., 2006, 120(3): 1315-1321.

[8] SIDERIUS M, SONG H, GERSTOFT P. Adaptive passive fathometer processing[J]. J. Acoust. Soc. Am., 2010, 127(4): 2193-2200.

[9] 赵梅, 胡长青, 屈科. 浅海海底单参数模型分析与研究[J]. 声学技术, 2014, 33(6): 494-498.ZHAO Mei, HU Changqing, QU Ke. Analysis of single parameter seabed model in shallow water[J]. Technical Acoustics, 2014, 33(6):494-498.

[10] 屈科, 胡长青, 赵梅. 浅海海底单参数快速反演模型研究[J]. 声学技术, 2012, 31(2): 152-155.QU Ke, HU Changqing, ZHAO Mei. Single parameter rapid inversion model of shallow water[J]. Technical Acoustics, 2012, 31(2):152-155.

[11] LONG Jianjun, LI Ganxian. Theoretical relationship between sound velocity and physical properties of submarine sediment[J].Chinese Journal of Acoustics, 2015, 34(4): 401-412.

[12] HAMILTON E. L. Sound velocity and related properties of marine sediments[J]. J. Acoust. Soc. Am., 1998, 72(6): 1891-1904.

[13] 汪德昭, 尚尔昌. 水声学[M]. 北京: 科学出版社, 1981, 32-34.WANG Dezhao, SHANG Erchang. Underwater Acoustic[M].Beijing: Science Press, 1981, 32-34.

[14] 金翔龙. 东海海洋地质[M]. 北京: 海洋出版社, 1992:185-196.JIN Xianglong. Marine geology of East China sea[M]. Beijing:China Ocean Press, 1992: 185-196.