线阵相控换能器阵列参数对聚焦性能的影响分析

魏文卿，景洪伟，伍 凡

(1. 中国科学院光电技术研究所，四川成都610209；2. 中国科学院大学，北京100049)

0 引 言

作为无损检测的方法之一，超声检测已广泛用于医疗、工业无损检测、复合材料缺陷检测等领域[1-3]。近年来，超声相控阵技术以其灵活的声束偏转及聚焦性能逐渐引起人们的重视，成为研究热点之一[4-6]。该技术通过电子系统控制换能器阵列中的各个阵元，按照确定好的延时法则发射和接收超声波，从而精确地控制声束偏转和聚焦到所检测的各个区域内，通过分析换能器接收到的超声信号，实现对材料的无损检测。国内外很多学者研究了换能器阵列参数(阵元尺寸、阵元间距、阵元数量，激活孔径、发射频率等)对换能器发射声场性能的影响，他们大都是从指向性理论出发来分析超声波的空间特性，而对聚焦性能的研究较少[7-9]。

本文首先对超声相控阵线阵换能器的声场特性进行了理论分析，通过仿真分析阵列参数对声束聚焦性能的影响，提出了换能器阵列参数的优化原则，并对参数优化后的相控阵换能器的声场性能进行实验测试，为超声相控阵缺陷检测时换能器的选择提供了参考。

1 超声相控阵检测原理

超声相控阵换能器的工作原理是基于惠更斯-菲涅耳原理。换能器由多个相互独立的压电晶片组合成阵列，每个晶片称为一个阵元，一般是由多个阵元组成的一维阵或二维阵。每个阵元有自己独立的发射和接收电路，通过软件控制各个阵元的超声发射和接收，实现对合成声束的偏转和聚焦控制[10]。

相控阵发射：超声相控阵运用多个阵元来产生和接收超声波。利用事先确定好的延时法则依次激励一个或几个阵元，产生确定相位的可控声波，所有阵元在检测对象中产生的超声声场相互干涉叠加，从而得到预期的波束入射角度和聚焦位置，形成发射声束偏转或聚焦等效果[11]。图1(a)中，换能器各阵元的激励时序是等间隔增加发射延时，使得合成波阵面偏转了一个角度，即相控发射声束偏转；图1(b)中，阵列换能器各阵元的激励时序类似于抛物线状，两端阵元先激励，逐渐向中间阵元加大延时，使得合成的波阵面指向一个曲率中心，即相控发射声束聚焦。

相控阵接收原理如图2所示。换能器发射的超声波遇到目标T后产生回波信号，其到达各阵元的时间存在差异。按照回波到达各阵元的时间差对各阵元接收信号进行不同的延时补偿，然后相加合成，就能将特定方向上的回波信号叠加增强，而将其他方向上的回波信号减弱甚至抵消[12]。

图1 相控发射偏转与聚焦Fig.1 Deflection and focusing of phased array transmission

图2 相控阵接收原理Fig.2 Schematic diagram of phased array reception

2 声场的数学模型

根据声场计算理论，一个有限尺寸的换能器辐射声场，可以按照惠更斯原理进行分析，即将换能器的有效辐射面，看作是无数点声源的组合，辐射场中某一点的声压是辐射面上所有点源在该点产生的声压叠加的结果。

由于相控阵换能器的口径和频率满足高频近似条件，因此表面辐射面积为S的整个换能器在场点P处产生的声压可以看成是各微元在场点P处叠加形成的总声压，可表示为瑞利积分[13]：

其中：ρ0为介质的密度；c为介质中的声速；uA为辐射面中心处的振速幅值；h为辐射微元ds中心到场点P的距离；ω为角频率；k为角波数(k=2π/λ)；

2.1 单源矩形换能器辐射声场计算

图3 单源矩形换能器和一维线阵换能器的声场计算坐标Fig.3 Acoustic field coordinates of single rectangular transducer and one-dimensional linear phased transducer array

图3为单源矩形换能器和一维线阵换能器的声场计算坐标。图3(a)所示为一单源矩形换能器辐射声源，其宽度为a，长度为l。取矩形中心O为坐标原点，矩形换能器所在平面为xOy面。场点P与坐标原点间的距离为r，位置矢量r与z轴正向的夹角为θ，P'点为P点在xOy平面内的投影，OP'与x轴正向的夹角为φ，e为辐射微元ds中心到坐标原点O的距离。

当r远大于矩形阵元尺寸时，图中的h可近似用阵元中心到场点的距离r来代替。至于相位部分，由图3(a)可得

当r＞＞a时，式(2)可以近似为

进一步推导得出

将式(3)、(4)代入式(1)，可以推导得出矩形换能器的辐射声压为

2.2 一维阵列换能器辐射声场计算

由第1节可知，当相控线阵换能器中各阵元采用抛物线状激励时序时，其合成的波阵面指向一个曲率中心，即可实现波束聚焦。计算分析得出相控线阵波束聚焦时，第n个阵元与第0个阵元之间的时间延迟Δtn为[14]

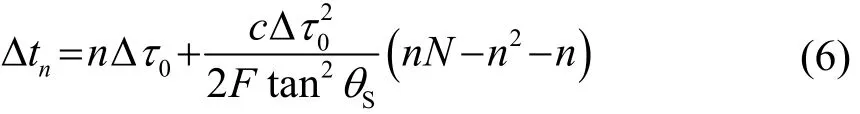
式中：F为阵列中心和聚焦点间的距离，即焦距；θS为声束偏转角；N为阵元总数；Δτ0为声束偏转时相邻两阵元之间的延迟时间，表示为

图3(b)所示为矩形阵元构成的相控一维线阵。根据声场计算理论并结合波束聚焦时的时间延迟，可得一维线阵换能器声束聚焦时的声场声压分布为[14]

3 阵列换能器参数对聚焦性能的影响

引入指向性函数D(θ,φ)来表示波束传播性能，根据声束聚焦时的声场分布和指向性函数的定义，由乘积定理可以推导出一维线阵换能器的归一化声束聚焦指向性函数为[15]

式(8)中，DF1(θ,φ)表示波束聚焦时单一矩形阵元的指向性函数，表达式为

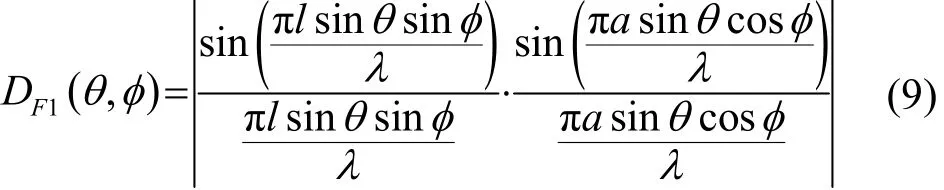
式(8)中，DF2(θ,φ)表示波束聚焦时简单点源线阵的指向性函数，表达式为

由式(8)可以看出，影响换能器声束聚焦指向性的阵列参数主要包括：阵元长度、阵元宽度、阵元间距和阵元数量。

3.1 阵元长度的分析

在工业无损检测应用中，利用超声相控阵列的聚焦性能时，应使波束聚焦在近场长度的2/3处之外，本研究中取焦距F等于近场长度ZTR(阵列参数为N=16、a=λ/4、d=λ/2、c=5700 m.s-1、f=10 MHz，此时，ZTR= 8 mm)。根据式(8)，阵元长度l取5a、10a、15a、20a等不同值时，换能器的波束聚焦指向性如图4所示。图4中D表示归一化声束聚焦指向性函数，即

由图4可知，当阵元长度非常小时，主瓣波束之外分布的能量较多，随着阵元长度的增加，主瓣波束之外分布的能量减小，主瓣宽度逐渐减小，当l=15a时，主瓣波束能量比较集中，波束具有良好的聚焦指向性。由式(8)可以看出，阵元长度l与xOz平面上线阵换能器的波束聚焦指向性函数无关，即l的变化不会对方向锐角、波束角、旁瓣级等波束方向参数产生影响。因此，当l继续增加时，由于波束的形状没有改变，波束的能量强度却有所减弱。为了获得良好的波束聚焦性能，一般可取阵元长度

3.2 阵元宽度的分析

根据式(8)，阵元宽度a取λ/8、λ/4、λ/2、2λ/3等不同值时，xOz平面上换能器的波束聚焦指向性如图5所示，取焦距F=15 mm(对应阵列参数为N=16，d=2λ/3，c=5700 m.s-1，f=10 MHz)。

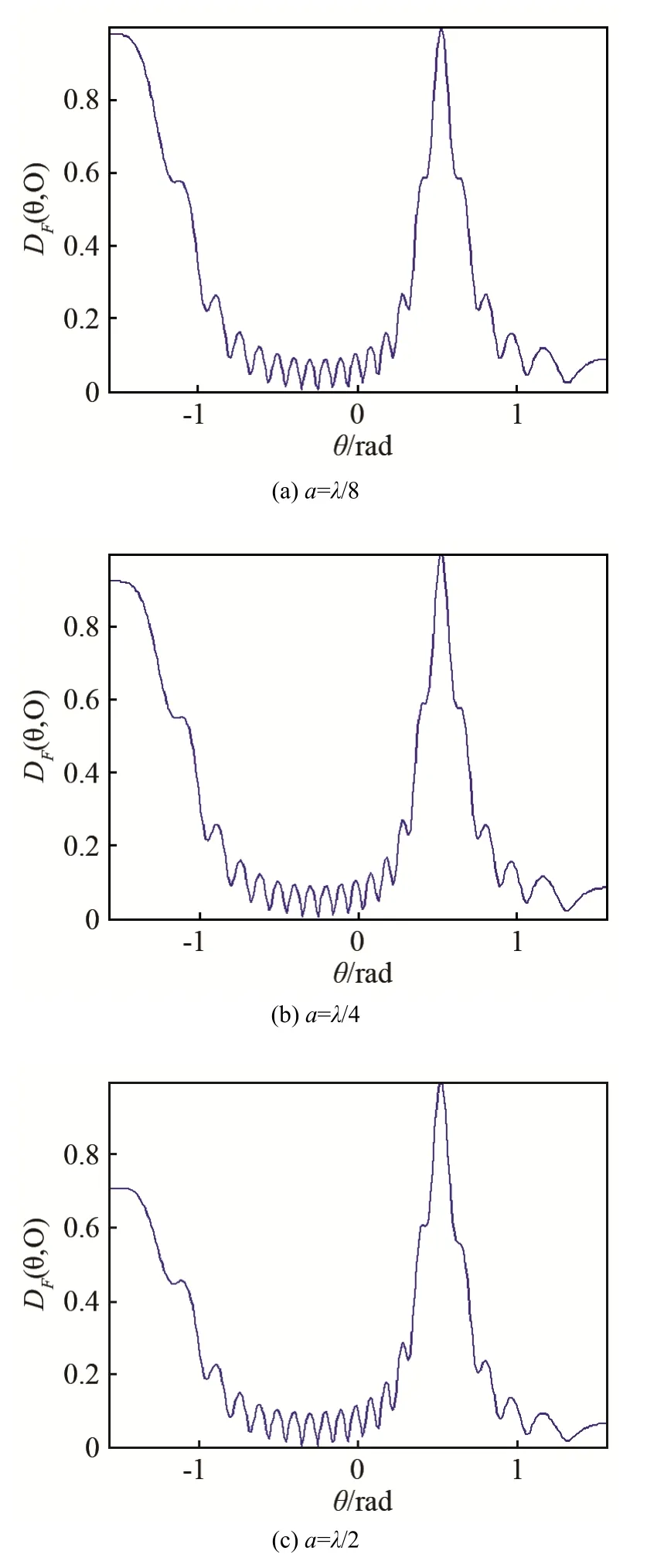
图5 不同阵元宽度的xOz平面上换能器的波束聚焦指向性图(d=2λ/3,θS = π /6, N=16, F=15 mm, c=5700 m/s, f=10 MHz)Fig.5 Beam focused directivity plots of transducer with different element widths in the plane of xOz

指向性理论分析表明，主瓣宽度和栅瓣的位置是由指向性图的零极点决定的[9]的调制作用不能改变零极点的位置，只能影响幅值。因此，当a＜λ时，阵元宽度对主瓣宽度、栅瓣存在与否都没有影响，导致随阵元宽度a的增大，波束聚焦指向性图中主瓣的形状基本不变，但是当a增大到一定程度时，由于阵元间距的限制，栅瓣幅值明显减小。因此，增大阵元宽度可以降低栅瓣幅值，进而改善换能器的聚焦性能，但根据换能器的实际制作要求，阵元宽度a不能超过阵元间距d。

3.3 阵元间距的分析

根据式(8)，阵元间距d取 0.04λ、0.1λ、0.5λ、2λ/3、λ、2λ时，xOz平面上换能器波束聚焦指向性如图6所示，焦距仍取F=15 mm。

由图6可见，当d=0.04λ时，整个声场空间的波束聚焦指向性极差，主瓣的范围很宽，不利于检测；随着d的增大时对应的方向锐角减小，导致主瓣宽度变窄，聚焦指向性增强；特别是d=0.5λ时，主瓣质量得到明显改善；当d=2λ/3时，虽然主瓣质量很好，但开始出现栅瓣，且主瓣质量变差，继续增加阵元间距时，波束聚焦指向性图中出现了许多杂乱波瓣，指向性更差。由此可见，存在一个消除栅瓣的临界阵元间距dmax，此时方向锐角最小，且无栅瓣出现。诸多研究表明[16-17]，临界阵元间距为

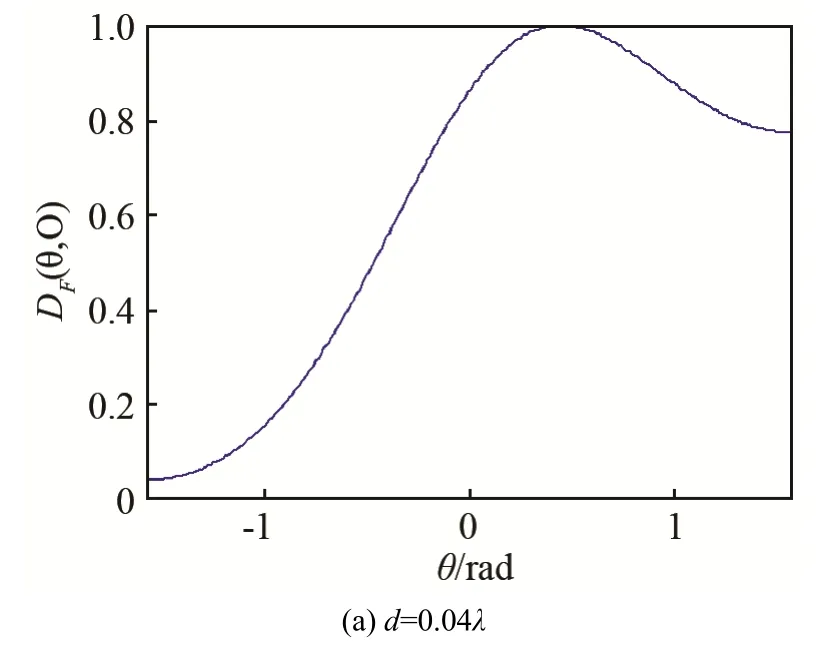
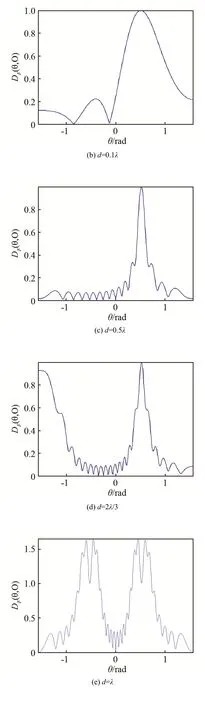
图6 不同阵元间距的xOz平面上换能器波束聚焦指向性图(θS = π /6, a=0.25λ, N=16, F=15 mm, c=5700 m/s, f=10 MHz)Fig.6 Beam focused directivity plots of transducer with different element spacings in the plane of xOz

当阵元数量较多为声束的最大偏转角度。

3.4 阵元数量的分析

阵元数量会影响阵列换能器的近场长度，不同的阵元数量N会产生不同的近场长度ZTR，进而对应不同的焦距F(本文中取F=ZTR)。

根据式(8)，当阵元数量N取 4、8、16、32、64、128时，xOz平面上换能器的波束聚焦指向性如图7所示。

由图7可见，N=4时，换能器波束聚焦指向性极差，没有出现主瓣且旁瓣很大；N=8时，波束聚焦指向性开始改善，但主瓣很宽；随着N的继续增加(N≥16 )，方向锐角减小，导致主瓣宽度变窄，同时N的增加会导致第一旁瓣的峰值减小，进而使旁瓣的幅值减小，但由于N的增加不会对声场的能量分布产生影响，进而对栅瓣的幅值不会产生影响；当N≥64 之后，主瓣宽度变窄的幅度非常小。因此，为了使波束具有最小的方向锐角，且无栅瓣出现，在给定的阵列孔径中应安排尽可能多的阵元数量，同时考虑系统的成本和复杂性，阵元数量不宜取太多。

图7 不同阵元数量的xOz平面上换能器波束聚焦指向性图(θS = π /6, a=λ/2, d=2λ/3, c=5700 m/s, f=10 MHz)Fig.7 Beam focused directivity plots of transducer with different elements numbers in the plane of xOz

基于线性换能器声束聚焦性能的仿真分析，得出换能器阵列的优化参数为：l≥ 15a，a≤d，d≤2λ/ 3 ，N≥16。本文选取了符合优化参数的相控阵换能器(型号为：10L64-I1，阵列参数为：f=10 MHz，N=64，d=0.5 mm，l=7 mm)，并采用已有的超声相控仪TomoScan FOCUS LT对其声束聚焦性能进行了实验测试，测试结果如图8所示。

由图8可以看出，该阵列换能器表现出了较为良好的声束聚焦特性，主瓣明显且较窄，旁瓣幅值很低，没有出现栅瓣，与仿真分析的结果基本吻合。

图8 相控阵换能器的声场性能测试结果Fig.8 Acoustic field testing result of phased array transducer

4 结 论

本文主要对超声相控阵换能器的聚焦性能进行了仿真分析，得出不同的阵列参数对换能器声束的聚焦指向性的影响，并提出了如下的改善换能器声场性能的措施。

(1) 为了获得良好的波束聚焦性能，应使阵元长度l与阵元宽度a之比越大越好，一般可取

(2) 阵元宽度a越大，波束聚焦指向性越好，但原则上不得超过阵元间距d；

(3) 阵元间距d增大，聚焦波束主瓣宽度变窄，当d增大到2λ/3及以上时，开始出现栅瓣，且主瓣质量逐渐变差，故存在一个消除栅瓣的临界阵元间距，如式(11)所示；

(4) 阵元数量N越多，波束聚焦指向性越好，但不会对波束的栅瓣特性产生影响。

基于以上分析结果，并结合实际应用，选取了型号为10L64-I1的相控阵换能器，对其声场性能进行了实验测试，结果表明该换能器具有良好的声束聚焦性能，能够有效地用于材料的缺陷检测中。

参考文献

[1] 冯若. 超声手册[M]. 南京: 南京大学出版社, 1999: 313-324.FENG Ruo. Ultrasonics Handbook[M]. Nanjing: Nanjing University Press, 1999: 313-324.

[2] 沈玉娣. 现代无损检测技术[M]. 西安: 西安交通大学出版社,2012: 1-13.SHEN Yudi. Modern nondestructive testing technology[M]. Xi’an:Xi’an Jiaotong University Press, 2012: 1-13.

[3] 敬人可, 李建增, 周海林. 超声无损检测技术的研究进展[J]. 国外电子测量技术, 2012, 31(7): 28-30.JING Renke, LI Jianzeng, ZHOU Hailin. Research progress of ultrasonic ndt technology[J]. Foreign Electronic Measurement Technology, 2012, 31(7): 28-30.

[4] 潘亮, 董世运, 徐滨士, 等. 相控阵超声检测技术研究与应用概况[J]. 无损检测, 2013, 35(5): 26-29.PAN Liang, DONG shiyun, XU Binshi, et al. The review of study and application of phased array ultrasonic testing technology[J].Nondestructive Testing, 2013, 35(5): 26-29.

[5] DRINKWATER B W, WILCOX P D. Ultrasonic arrays for non-destructive evaluation: A review[J]. NDT & E International,2006, 39(7): 525-541.

[6] 靳世久, 杨晓霞, 陈世利, 等. 超声相控阵检测技术的发展及应用[J]. 电子测量与仪器学报, 2014, 28(9): 925-933.JIN Shijiu, YANG Xiaoxia, CHEN Shili, et al. Development and application of ultrasonic phased array inspection technology[J].Journal of Electronic Measurement and Instrumentation, 2014,28(9): 925-933.

[7] 宋志明, 王黎, 周小红, 等. 超声相控阵技术中的声场仿真[J]. 压电与声光, 2011, 34(4): 565-570.SONG Zhiming, WANG Li, ZHOU Xiaohong, et al. Simulation for sound-field of ultrasonic phased array technique[J]. Piezoelectrics & Acoustooptics, 2011, 34(4): 565-570.

[8] 温姣玲, 卢超, 何方成, 等. 航空复合材料层压板钻孔分层缺陷相控阵检测参数优化[J]. 玻璃钢/复合材料, 2017(2): 21-25.WEN Jiaoling, LU Chao, HE Fangcheng, et al. Research on optimal parameters of ultrasonic phased array detection of drilling-induced delamination in composite laminates[J]. Fiber Rein-forced Plastics/Composites, 2017(2): 21-25.

[9] 孙芳. 超声相控阵技术若干关键问题的研究[D]. 天津: 天津大学,2012.SUN Fang. Research on several key issues of ultrasonic phased array technology[D]. Tianjin: Tianjin University, 2012.

[10] 王悦民, 李衍, 陈和坤. 超声相控阵检测技术与应用[M]. 北京:国防工业出版社, 2014: 2-4.WANG Yuemin, LI Yan, CHEN Hekun. Ultrasonic phased array inspection technology and application[M]. Beijing: National Defence Industry Press, 2014: 2-4.

[11] 李衍. 超声相控阵技术[J]. 无损探伤, 2008, 32(2): 24-29.LI Yan. Ultrasonic phased array technology[J]. Nondestructive Testing, 2008, 32(2): 24-29.

[12] 何正权, 刘志宏, 袁勤. 数字多声束形成技术的研究及意义[J]. 中国超声医学杂志, 1997, 13(8): 14-16.HE Zhengquan, LIU Zhihong, YUAN Qin. Digital multi-forming technique research and its significance[J]. Chinese Journal of Ultrasound in Medicine, 1997, 13(8): 14-16.

[13] 丁辉. 计算超声学[M]. 北京: 科学出版社, 2010: 18-22.DING Hui. Computational Ultrasonics[M]. Beijing: Science Press,2010: 18-22.

[14] 黄晶. 超声相控阵理论及其在海洋平台结构焊缝缺陷检测中的应用研究[D]. 上海: 上海交通大学, 2005.HUANG Jing. Research on theory of ultrasonic phased array and its application in detecting weld defects of offshore platform structure[D]. Shanghai: Shanghai Jiao Tong University, 2005.

[15] 陈榕基. 基于超声相控技术的阵列探头参数优化设计研究[D]. 广州: 华南理工大学, 2012.CHEN Rongji. Research on optimal parameters design of array probe based on ultrasonic phased array[D]. Guangzhou: South China University of Technology, 2012.

[16] WOOH S C, SHI Y. Optimum beam steering of linear phased arrays[J]. Wave Motion, 1999, 29(3): 245-265.

[17] AZAR L, SHI Y, WOOH S C. Beam focusing behavior of linear phased arrays[J]. NDT & E International, 2000, 33(3): 189-198.