基于粒子群最小二乘支持向量机的前视声呐目标识别

石 洋，胡长青

(1. 中国科学院声学研究所东海研究站，上海201815；2. 中国科学院大学，北京100049)

0 引 言

声呐图像目标识别就是将数字图像处理和模式识别技术应用到水下环境中。随着多波束高频声呐及高分辨率成像声呐技术的发展，以及军事和民用对水下目标探测应用的需求，声呐图像识别逐渐成为热门的研究领域。如今的声呐智能系统不仅要求能够获取声图像和声信息，还要求能够对这些信息进行处理、特征提取及分类识别[1]。但受限于复杂多变的水声信道、多途效应、混响和环境噪声，水下声成像具有对比度差、边界模糊、信息残缺等缺点。因此，传统的光学图像处理方法需经过改动后才能适用于声呐图像；而各种识别算法的效果受目标特征的影响很大，这也给声呐图像识别带来了很大的困难。目前常用的识别方法有模板匹配法、神经网络法、模糊识别法、特征统计法等。至今仍没有统一公认的最优方法[2]。

本文将基于前视声呐进行图像处理与识别，以实现对特定水下目标的探测。通过预处理和图像分割获得清晰完整的目标区域，在此基础上提取特征，并利用粒子群算法和最小二乘支持向量机完成分类识别。

1 声呐图像处理

声波在复杂的水下环境传播时，存在着大量混响与衰减；同时受到声成像特性的影响，水声图像普遍存在着分辨率低、细节不清晰、干扰强等问题。因此，声呐图像预处理以及选择合适的算法进行图像分割是准确分析图像信息的基础。

1.1 声呐图像的获取

本文将铁架、网兜和笼子作为目标，研究无大幅度形变的水下物体识别。实验于某湖上试验船上进行，采用 M3多波束前视声呐进行探测。M3多波束前视声呐的探测距离为0.2～150 m，分辨距离为0.01 m，工作频率为500 kHz，发射的信号类型为单频矩形(Continuous Wave，CW)脉冲和线性调频(Linear Frequency Modulation，LFM)脉冲，声波发射的水平张角为 140°，竖直张角为30°。用细绳牵引铁架和网兜运动，以获取不同距离角度下的运动目标图像；同时固定笼子，获取同一水下环境不同时刻的静止目标图像。

1.2 图像预处理和目标分割

图像的预处理包括去噪和增强两部分：采用 3×3中值滤波消除噪声和畸变；采用分段灰度线性变换[3]和模糊集算法[4]增强图像。预处理可提高图像的对比度和边缘清晰度，突出目标信息、抑制背景。采用融合空间信息的模糊 C均值算法进行目标分割。经典的模糊C均值算法将图像的像素划分为C个子类，迭代地求出每个子类的聚类中心和每个像素的模糊隶属度，使得目标函数最小。最终按照最大隶属度原则对像素进行聚类划分，完成图像分割。在该算法的基础上，引入空间邻域项修改目标函数，使得算法的抗噪性和稳定性更强。选取像素点xj的邻域均值作为空间信息，聚类中心表示为[5]

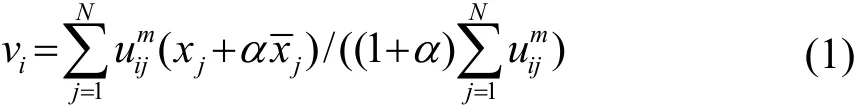
此时xj相对于聚类中心vi的模糊隶属度表示为[5]

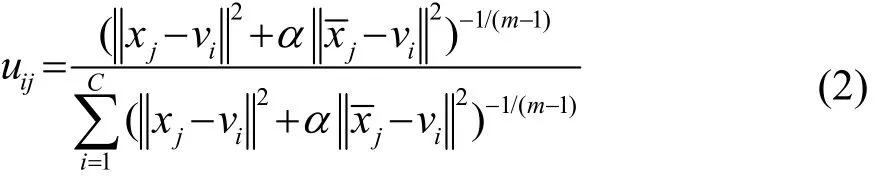
目标函数表示为[5]

式(1)、(2)、(3)中：C是聚类个数；N是像素个数；m是权重指数；α是控制参数。本节详细的算法见参考文献[3-5]。由于本次实验获取的前视声呐图像没有阴影区，故将其分割成目标区和背景区两部分。分割后得到了二值图，为了方便后续特征提取时的计算，将背景像素值设置为0，目标像素值设置为1。

1.3 提取连通分量

由于分割后的图像可能还存在着其他干扰，因此提取二值图中符合条件的连通分量是直接获取目标区域的关键。针对目标区域存在断裂的情况，对整幅图片做闭运算，连通孔洞和缝隙，使目标区域尽可能形成一个整体。以物体连通分量大小为先验条件，对标记出的连通分量进行比对排查，截取符合条件的目标区域。

1.4 处理结果

采集三类水下目标在不同时刻的声呐图像，获取铁架图像127幅、笼子图像84幅、网兜图像141幅。所有图像处理分割后效果如图1所示。

部分样本图像截取的目标区域如图2所示。

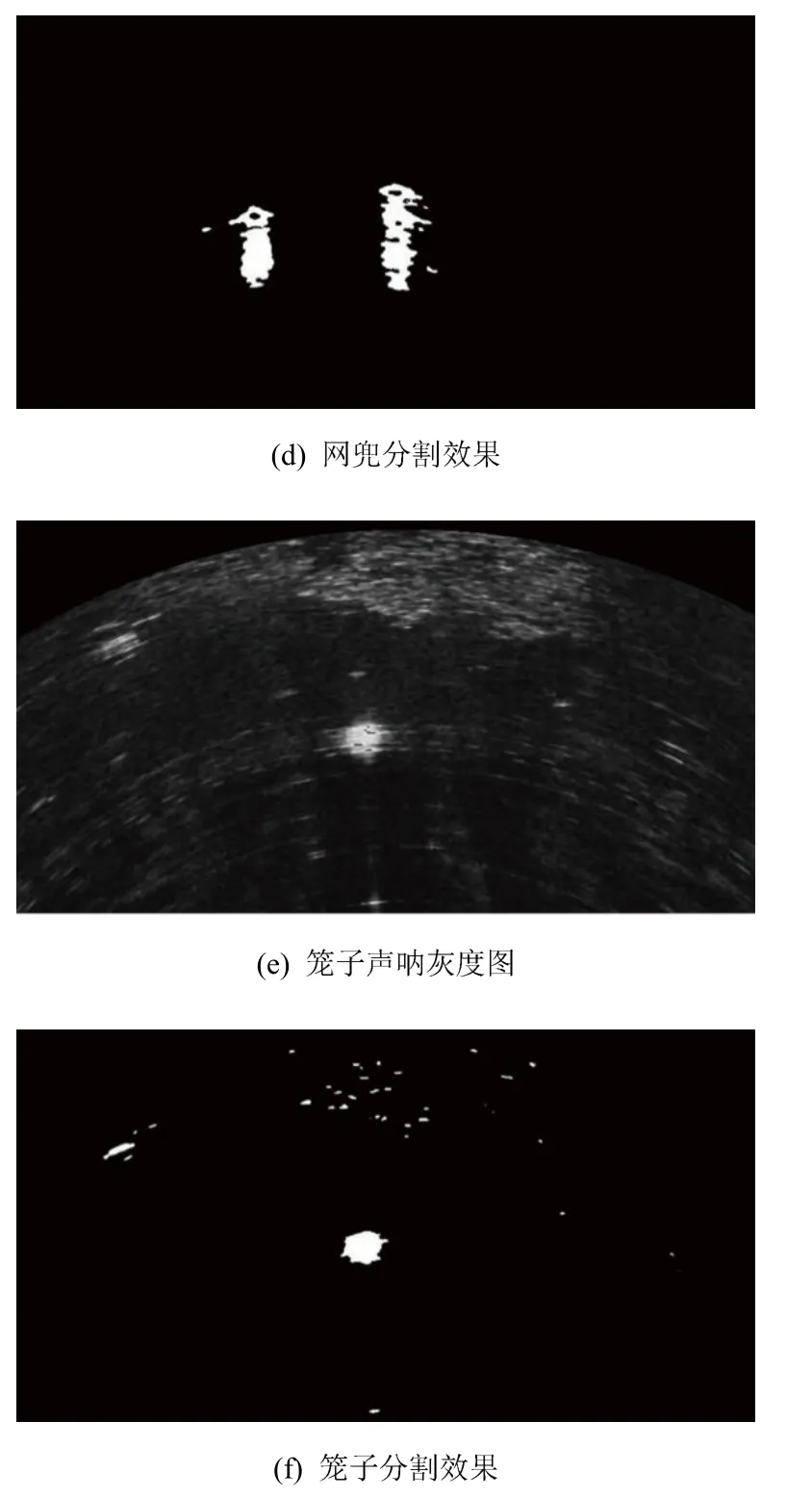
图1 三种目标图像灰度图及分割效果Fig.1 Grayscale and segmentation results of three kinds of target images

图2 部分样本图像目标区域Fig.2 Target areas of some samples

2 特征提取

特征提取就是在给定对象的属性中，寻找能区别于其他对象的不同特点或特性。特征提取的一般原则是同类别之间差异较小，不同类别之间的差异较大。

2.1 声呐目标特征分析

声呐目标的图像特征一般包括：形状特征(区域形状特征和轮廓形状特征)、纹理特征(描述物体表面灰度的变化)和不变性特征(不变矩、转动惯量等)。分割成目标区和背景区的二值前视声呐图像不具备纹理特征；而同一水下物体在不同时刻、不同位置的图像内容都会有差别，因此不变性特征也不适用。由于分割后的目标区域完整、边界清晰，不同目标之间形状差别明显，同一目标虽然存在成像差异但形状基本相似，故本文主要提取目标的区域形状特征。

2.1.1 形状参数F

大小为Ma×Na的二值图像的面积A定义为

即的个数之和。周长表示连通区域边界像素的集合，8-连通周长Pa定义为

式(5)中，R是图像的一个区域是像素点(x,y)的 8邻域。利用一个区域的面积与具有相同周长的一个圆的面积之比，可度量一个区域的形状参数[3]。此时将形状参数F定义为

式(6)描述的是目标图像和圆形的偏离程度。当目标区域为圆形时，F=1，为其他形状时，F＞1，且偏离量越大，其形状与圆的差别就越大。

2.1.2 最大连通分量的外接矩形

对目标区域进行闭运算，使得区域内的连通分量尽可能形成一个整体。此时，区域内最大连通分量的外接矩形可反映物体的形状信息。选取其长和宽为特征。

2.1.3 连通区域的外接矩形面积和

考虑到同一物体声呐图像在成像完整和成像残缺时面积大小会有差异(如图2所示)，故通过闭运算处理后，选取目标区域内所有连通分量的外接矩形面积之和作为特征，可在一定程度上减少同类目标因像素差导致的区域面积差异。

2.2 特征提取

提取所有声呐图像目标区域的形状特征作为分类识别的数据。部分样本特征如表1所示(用边界上的像素数目表示长度，区域中的像素总数表示面积)。

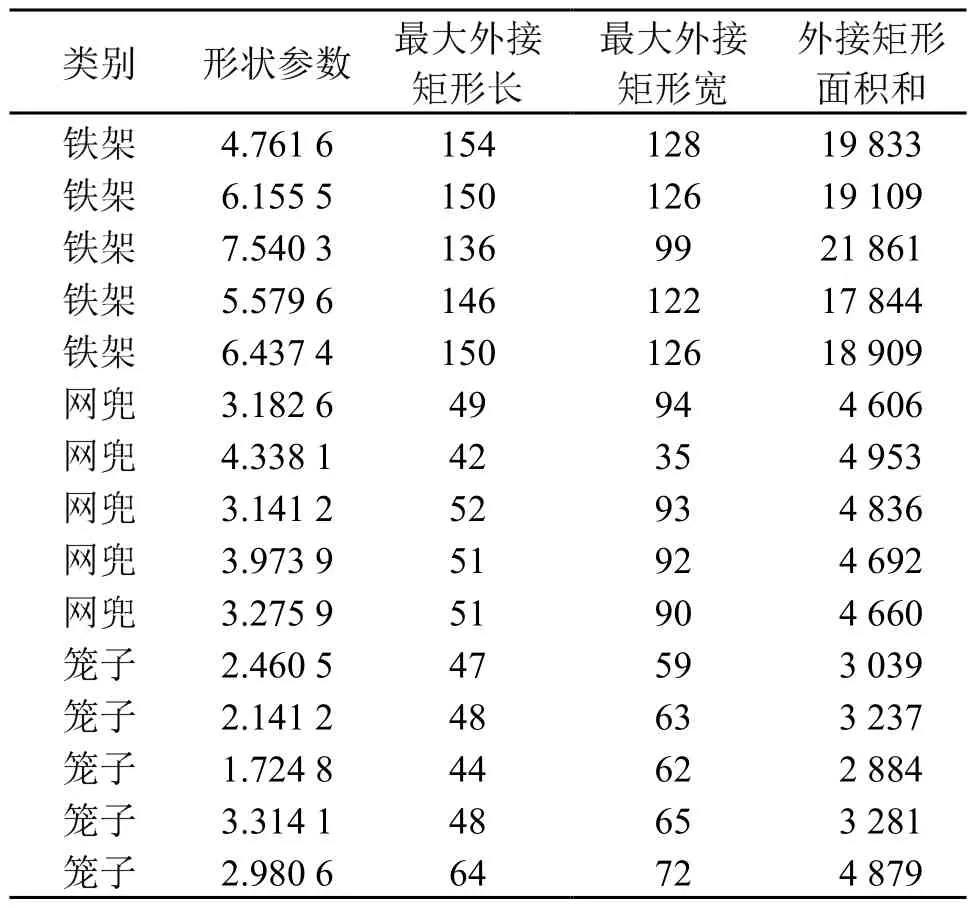
表1 部分目标样本特征Table 1 Features of some target samples

识别前对所有特征在[0,1]区间内进行归一化处理。采取的映射如下：

3 分类识别

3.1 支持向量机分类

支持向量机是一种能够很好地解决小样本、非线性、高维数等问题的机器学习方法。最小二乘支持向量机(Least Squares Support Vector Machine，LSSVM)是支持向量机的一种拓展，将误差平方引入到标准支持向量机的目标函数中，使得不等式约束变为等式约束，则原求解过程中的二次规划问题变成了求解线性方程组的问题。这样降低了学习难度，提升了求解速度。其分类思想如下[6]：

已知数据集，N为样本个数，样本xk对应的类别yk∈{-1 ,1}，利用最优超平面式(8)对样本进行分类，分类决策函数为式(9)：

式中：ω为法向量，b为偏移量。对于非线性问题，通过映射函数ϕ(x)将样本映射到高维特征空间，在该空间数据集线性可分。此时分类问题即求解优化函数：

其中：γ为正则化参数，ek为误差变量。其拉格朗日多项式为：

式中，αk为拉格朗日乘子。根据优化条件

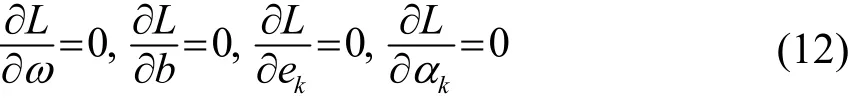
分别解得：

消去ω和ek，可得线性方程组

其中：I为单位矩阵，为核矩阵，为核函数，求解方程组得到系数此时分类函数为[6]

标准的LSSVM解决的是二分类问题。对于多分类的情况，主要采取多目标优化和组合编码的方法。本文选择最小输出编码(Minimal Output Code，MOC)实现多分类[7]。核函数则选择径向基函数(Radial Basis Function，RBF)，即

在LSSVM模型中，正则化参数γ和核参数σ对模型分类的精度影响很大，选择合适的模型参数是构造分类器的关键[8]。将特征提取得到的数据分为训练集和测试集，如表2所示。

表2 三种目标图像的特征提取数Table 2 The number of feature extraction for three kinds of target images

选取γ=1，σ2=0.1，LSSVM能够从172个测试样本中识别出145个，准确率为84.30%。识别结果如图3所示。

选LSSVM能够从172个测试样本中识别出161个，准确率为93.60%。识别结果如图4所示。

由图3、图4可知，在实际应用中γ和σ对LSSVM 的分类性能有着显著的影响。本文将采用粒子群算法(Particle Swarm Optimization, PSO)对这两个参数进行优化。

3.2 粒子群算法

粒子群算法[9]属于进化算法的一种，其本质是随机搜索的全局优化算法。该算法收敛速度快且容易实现，通用性好，适合处理多目标优化问题。

3.2.1 算法思想

该算法的基本思想是通过一个群体内个体之间的协作和信息共享来寻找最优解。在一个D维目标空间中有 S个粒子，第i个粒子的飞行速度为，位置为其速度会根据历史经验进行动态调整，并且粒子有逐渐向其最优搜索位置靠近的趋势。当前粒子搜索到的自身最优位置称为个体极值pbest，当前整个粒子群搜索到的最优位置称为全局极值gbest，其表达式为

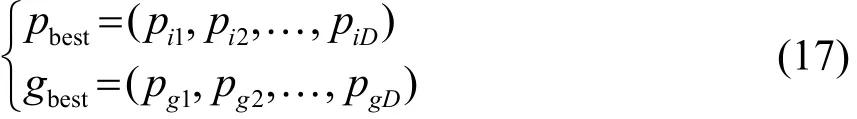
图4 最小二乘支持向量机的识别结果2(正则化参数γ=100，核参数σ2=60)Fig.4 Recognition result 2 of LSSVM for γ=100 and σ2=60

同时每个粒子还有一个由目标函数决定的适应值(fitness value)。根据两个极值，利用式(18)和式(19)更新速度和位置：

式中：c1、c2为学习因子；r1、r2为[0,1]范围内的均匀随机数；vid、xid和pid分别为第i个粒子在第d维的速度、位置和个体极值；pgd为第d维的全局极值；此处的ωpso为惯性权重，调控vid(t)对vid(t+1 )的影响，ωpso值越大，全局寻优能力越强，局部寻优能力越弱；ωpso值越小则反之。由式(18)可看出，粒子速度的更新分别由自身运动惯性、自身历史经验和群体历史经验这三部分共同作用。PSO算法仅仅利用个体信息和群体信息这两个极值便可通过迭代自行搜索和确定参数。

3.2.2 粒子群LSSVM算法步骤

粒子群LSSVM算法基本流程如下：

(1) 搜索空间设置为二维，分别对应γ和σ2的值。初始化参数：学习因子c1=1 .5、c2=1.7分别反映了PSO算法的局部搜索能力和全局搜索能力；进化次数为 200；种群数量size= 20；惯性权重ωpso= 1；γ的取值范围为[0.1, 100]，σ2的取值范围为[0.01, 1000]；迭代终止误差为10-3；

(2) 随机产生位置和速度，将训练集数据输入至LSSVM构造分类模型；利用该模型对测试集数据进行分类，以分类准确率作为每个粒子的适应度值

(3) 对于每个粒子，用适应度值和个体极值pbest进行比较，若，则用替换pbest；

(4) 用和全局极值gbest进行比较，若，则用fPSO(i)替换

(5) 根据式(18)和式(19)更新粒子速度vi和位置xi；

(6) 当误差足够小或者达到进化次数时退出；否则重新计算并再次比较更新。

4 识别结果

图5为粒子群算法进行参数寻优时的粒子轨迹曲线。

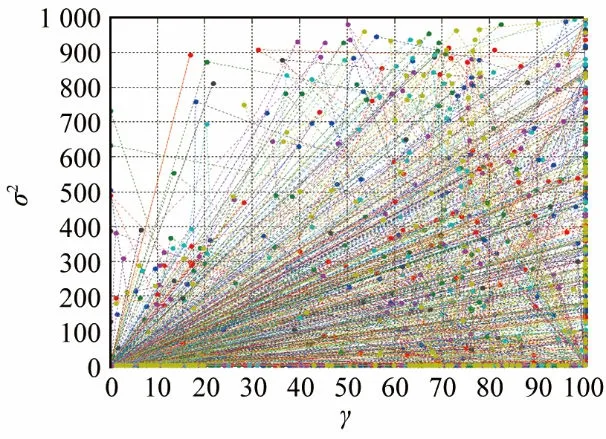
图5 粒子群优化的轨迹曲线Fig.5 PSO trajectory curves

图6 粒子群优化的适应度曲线Fig.6 PSO fitness curves

图6为算法的适应度收敛曲线，反映了PSO的进化过程。平均适应度为所有粒子每一代适应度的平均值；最佳适应度为所有粒子每一代的最大适应度值[10]。由图6可知，大约在110次进化后，最佳适应度即测试集分类准确率逐渐趋于平稳。

经过PSO优化，最终选择此时能从172个测试样本中识别出170个，两个网兜图像被误分成笼子图像，准确率达到了98.84%，最终识别结果如图7所示。

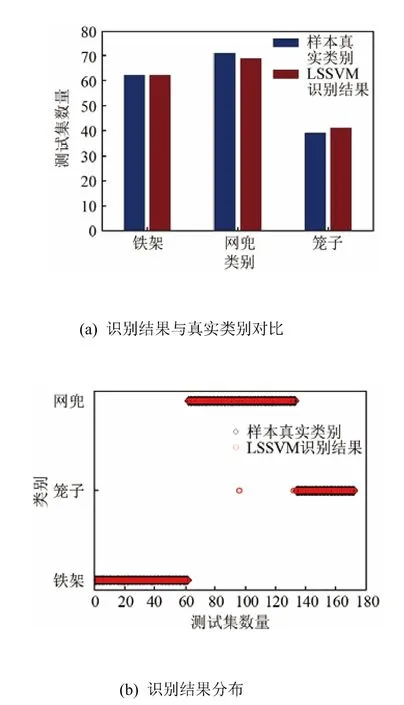
图7 粒子群优化处理后的最终识别结果Fig.7 Final recognition result after PSO processing

5 结 论

本文通过前视声呐获取水下目标的声图像信息，实现了完整的目标识别过程。经过图像预处理和基于融合空间信息的模糊C均值算法分割，得到了具有较好视觉效果的图像，图像中目标区域突出，形状清晰；截取分割后二值图中符合条件的连通分量作为目标区域，提取区域形状特征作为特征向量；将测试集样本的分类准确率作为适应度值，利用粒子群算法优化最小二乘支持向量机的模型参数。最终的分类实验证明，本文构造的最小二乘支持向量机多分类模型的识别准确度能够达到98.84%，较好地满足了水下目标识别效果的要求。在实际应用中，为无大幅度形变的水下目标探测提供了一定的参考。

参考文献

[1] 卢迎春, 桑恩方. 基于主动声纳的水下目标特征提取技术综述[J].哈尔滨工程大学学报, 1997, 18(6): 43-54.LU Yingchun, SANG Enfang. Feature extraction techniques of underwater objects based on active sonars an overview[J]. Journal of Harbin Engineering University, 1997, 18(6): 43-54.

[2] 刘晨晨. 高分辨率成像声纳图像识别技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2006: 17-18.LIU Chenchen. Study on image recognition technique of high resolution imaging sonar[D]. Harbin: Harbin Engineering University,2006: 17-18.

[3] 冈萨雷斯. 数字图像处理[M]. 3版. 北京: 电子工业出版社, 2011:68-69; 532.GONZALEZ R C. Digital image processing, [M]. third edition.Beijing: Publishing House of Electronics Industry, 2011: 26-29;532.

[4] 张铁栋, 秦再白, 朱炜. 基于模糊算法的水声图像增强[C]//全国图象图形学学术会议. 2005.ZHANG Tiedong, QIN Zaibai, ZHU Wei. A sonar image enhancement algorithm based on fuzzy set[C]//International Conference on Image and Graphics. 2005.

[5] CHEN S, ZHANG D. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure[J]. IEEE Transactions on Systems Man and Cybernetics Part B, 2004, 34(4): 1907-1916.

[6] SUYKENS J A K, VANDEWALLE J. Least squares support vector machines classifiers[J]. Neural Network Letters, 1999, 9(3):293-300.

[7] HSU C W, LIN C J. A comparison of methods for multiclass support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 45-54.

[8] 顾燕萍, 赵文杰, 吴占松. 最小二乘支持向量机的算法研究[J]. 清华大学学报(自然科学版), 2010, 50(7): 1063-1066.GU Yanping, ZHAO Wenjie, WU Zhansong. Least squares support vector machine algorithm[J]. Tsinghua University (Sci&Tech),2010, 50(7): 1063-1066.

[9] KENNEDY J, EBERHART R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks, 1995.Proceedings. IEEE, 2002, 4: 1942-1948.

[10] 郑含博, 王伟, 李晓纲, 等. 基于多分类最小二乘支持向量机和改进粒子群优化算法的电力变压器故障诊断方法[J]. 高电压技术,2014, 40(11): 3424-3429.ZHENG Hanbo, WANG Wei, LI Xiaogang, et al. Fault diagnosis method of power transformers using multi-class LS-SVM and improved PSO[J]. High Voltage Engineering, 2014, 40(11): 3424-3429.