闭口风洞声学测量中的阵列设计

季建朝，王明新，周永清

(1. 清华大学航天航空学院，北京100084；2. 陆军航空兵学院，北京101123)

0 引 言

声传感器阵列是气动声学测量的关键设备[1]。在测量过程中，信号声源通常具有很宽的频率范围，因此要求阵列能够在较宽的频率范围内对声源准确地识别与定位，这取决于硬件设计和数据优化两方面[2]。对于阵列设计，声传感器的布局方式比声传感器的选择更为重要[3]，不同的布置方式会影响阵列旁瓣及其识别声源频率的范围。早期的二维声传感器阵列有矩形、十字交叉形、环形阵列等[4]，研究表明任何规则排列的阵列都不可能满足最优设计准则[5]。人们通过研究找到了一些设计方案，最经典的阵列模型为螺旋线型阵列[6]。在阵列单元数给定的情况下，螺旋线型阵列对于抑制旁瓣以及获得较大的动态范围极其有效。多臂螺旋线阵列结合了螺旋线型阵列和奇数个声传感器单元圆形排列所形成的阵列优点，在实际工程领域中应用广泛[7]。

阵列成像结果主要通过三个指标来判断优劣[8]：一是阵列分辨率，指阵列对于声源空间分布的辨别能力，由波束宽度和声波相对于阵列的入射角度所决定(主瓣峰值向下3 dB对应的宽度为波束宽度)；二是阵列对旁瓣的抑制，指阵列对于非声源方向声能的抑制能力；三是抗空间混叠能力，代表了阵列对声源位置的指向性强弱。阵列按照以上指标进行的最优化设计往往按照圆形或规则形状进行，这些形状并不一定适合已经建好的风洞和测量模型。传统的测量方案往往根据风洞壁面口径将阵列按照设计形状进行等比例缩放，或者采用已经制作好的阵列测量不同的声源分布，这样做容易造成声传感器空间采样的不均匀，影响波束形成结果，因此在已有风洞基础上对阵列进行设计更具有实用价值。

本文针对已经建好的闭口声学风洞提出了三种阵列布置方案，分别为不同口径的阵列相配合、椭圆形分布阵列、“窗口”型阵列，如图1所示。这三种方案基本满足了风洞声学的测量需求。通过仿真和实验，证明了所得结果较传统方法能更好地适应实际的风洞测量，使波束形成结果得到进一步改善，并且总结了影响阵列测量结果的一般性因素。

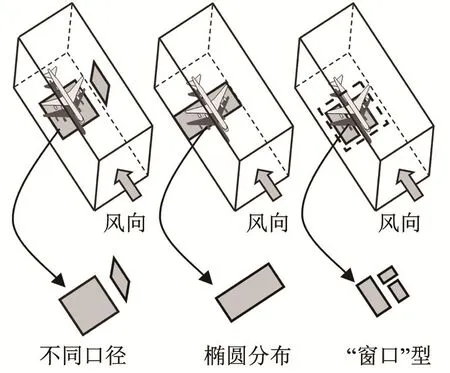
图1 阵列布置方案Fig.1 Array layout scheme

1 声源-阵列响应

考虑在x0点发射一个球面波信号s(t)，其周边也存在其它声源，混合声场用p(x,t)表示，在声场下面布有M个声传感器组成的阵列，坐标为方便起见，选择阵列的相位中心与阵列的中心重合。由声源s(t)诱导的声场在任意位置x处的声压由式(1)所示的波动方程所决定：

其中，Δt,m为声波到达x点的时间延迟。

由于声场的空间独立性，信号在传播过程中每个声传感器所采集信号的相位和幅值都在不断地变化，声源在x0位置，第m个声传感器所采集的声压信号可以表示为

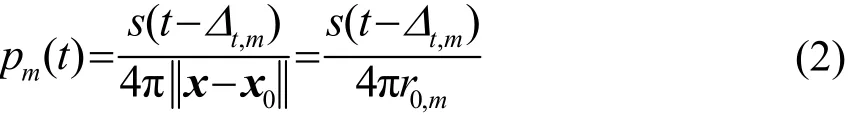
球面波波束形成的结果可表示为

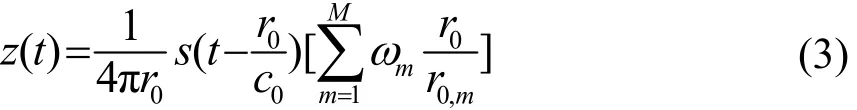
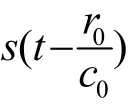
考虑到实际计算时并不知道声源位置，假设声源所处位置为x′，则波束形成可以描述为

“延时-相加”方法对虚拟平面进行扫描，通过计算声能最大点来定位声源的位置，如果计算点x′与声源点x0位置重叠时，声传感器的声能最大。需要注意的是：在此过程中不考虑壁面反射，并假设声源为紧致分布且相互独立的点源。对于非相互独立的声源，比如：相干、近距单极子、偶极子、四级子或者连续分布的声源，其相位、幅值都将产生变化[9]。

在闭口风洞中要考虑风速对于声传播的影响，假设风洞中气流为均匀流，来流速度大小为v0，声压满足如下波动方程

式(5)的解为：

也就是将式(1)中的替换为R，其中为声传感器在直角坐标中的坐标值，为来流马赫数。

将式(6)代入式(4)，便可得到风洞中的声源-阵列响应

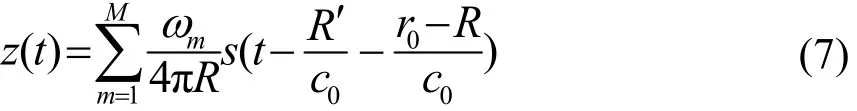
其中为计算点到声传感器的距离。

2 阵列设计最优准则

与阵列中M个声传感器位置所对应的伴随阵列向量为

式中，Xp称为xm的伴随阵列，不难看出Xp共有N2个取值，并且其中有N个为零，因此伴随阵列的最大单元数Pmax为

对于一个给定的阵列，假设P代表在阵列中伴随阵列单元数的实际值，于是存在如下关系：

其中，L是评价阵列性能的重要参数，当L=1时，阵列的伴随阵列单元数达到最大值。阵列的最优设计准则就是使它的伴随阵列具有最多的单元数。对数螺旋线阵列就满足了上述的最优准则[10]，其布局及伴随阵列如图2所示，声传感器在螺旋线上等弧长分布保证了传感器布局的零冗余，并且这种布局形式在宽频范围内适用。

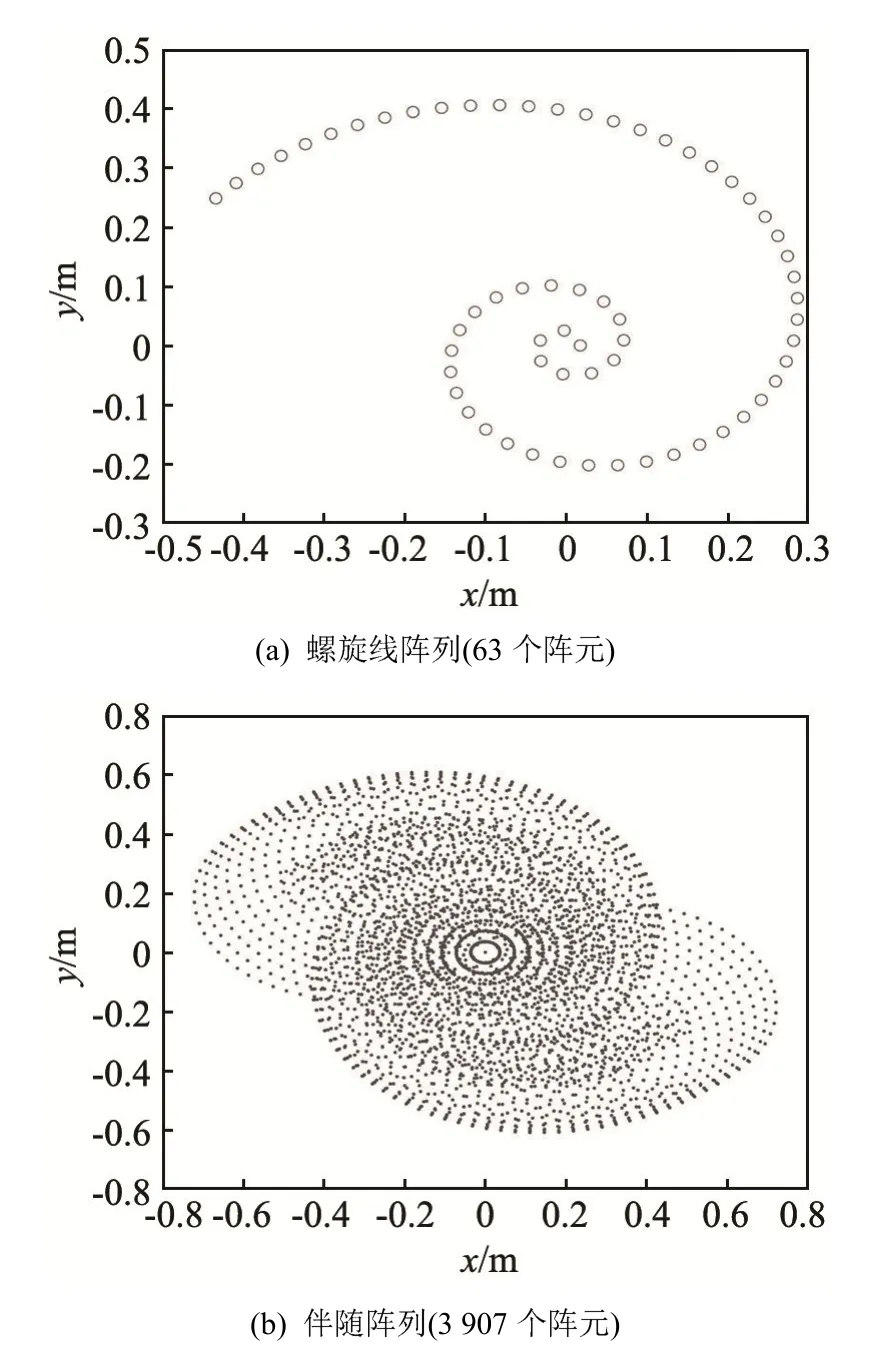
图2 螺旋线阵列及其伴随阵列Fig.2 Spiral array and its co-array

满足最优设计的阵列，在已有闭口风洞中进行声学测量时主要受阵元数量、阵列口径、阵元分布和风洞壁面开口四个因素影响。其中阵元数量主要影响阵列口径范围内的空间采样率，空间采样率过低时阵列的指向性变差，会出现空间混叠现象，阵元数量的多少在旁瓣抑制和抗空间混叠方面会起到重要作用，可以通过在阵列中增加或减少阵元解决。在阵元数量不变时，其它三个因素要根据测量对象权衡设计，保证测量结果达到最优。

3 闭口风洞阵列设计

3.1 双口径阵列

双口径阵列指的是根据声源性质以及测量的需求，采用大、小口径阵列进行声学测量[11]。口径变化会影响两个参数：分辨率和指向性，大口径阵列能够提高低频时主瓣的分辨率，小口径阵列的指向性更强，而分辨率与指向性不能同时得到改善。在低频时，如果想使主瓣更窄，阵列口径要做得大些，同时为了抑制相干噪声幅值、相位对结果的影响，阵列口径需要做得小些，小阵列不但便于在模型周围移动，而且能够避免扫描平面上背景噪声对结果的影响。

图3显示了基于多臂螺旋线阵列的单极子成像结果，声源频率为3 kHz，扫描平面距阵列0.7 m，扫描区域为1 m×1 m，图中Lp为声压级，单位为分贝(dB)。由图3(a)中可以看到，边长为1 m的小口径阵列指向性更强，对旁瓣的抑制能力更强，但是分辨率不高；图3(b)所示为边长2 m的大口径阵列，显然分辨率明显提高，但指向性变差，旁瓣水平整体偏高。在实际测量中，如果模型信号的跨度很大，最好的方法是针对高频和低频设置不同的阵列。要根据风洞壁面开口情况进行取舍，如果条件允许，可大、小口径阵列甚至声传感器通道结合使用。

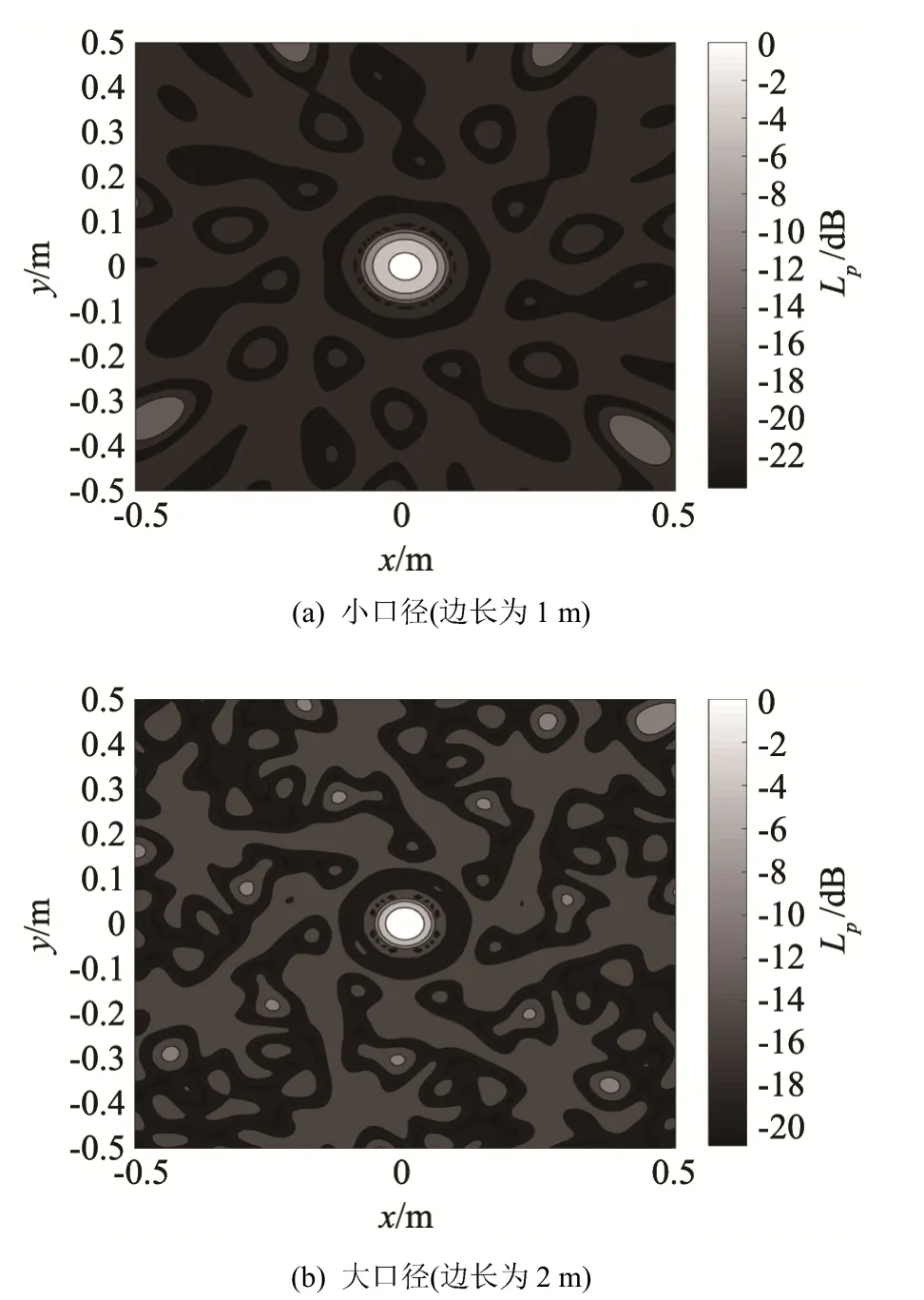
图3 不同口径阵列的成像结果Fig.3 Imaging results of different aperture arrays

3.2 椭圆形阵列

风洞壁面上允许布置阵列的空间往往不是正方形，而是长方形，如果在此空间内还按照正方形设计、布置阵列，则有部分空间会被浪费掉，此时要调整阵列布局。为了达到最佳空间采样，可采用将多臂螺旋线和椭圆相结合的方法。

由于椭圆运动轨迹上任意点到焦点F1和F2的距离和为固定值，所以具有两个坐标中心的方程在笛卡尔坐标下的椭圆方程为

其中，a和b分别为椭圆的长短半轴。如果椭圆的中心在原点，方程在极坐标下可表示为

其中，c=b/a为椭圆的长宽比，对于给定参数可得椭圆与螺旋线的交点极坐标，可在椭圆周线上布置阵元。

设在风洞上有1 m×0.5 m的长方形开口，在此开口上进行基于椭圆的多臂螺旋线阵列设计，其过程如图4所示。具体步骤可归纳为：(1) 按照长方形开口确定椭圆长宽比并绘制多臂螺旋线；(2) 在多臂螺旋线上采用阵列元等口径方法对传感器进行布局(如图4(a)所示)；(3) 获得阵元及其伴随阵列在长方形中的分布(如图4(b)所示)。

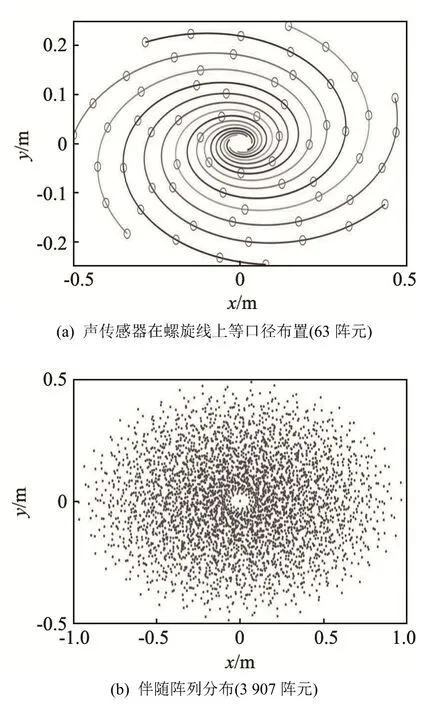
图4 基于椭圆的多臂螺旋线阵列及其伴随阵列Fig.4 Ellipse based multi-arm spiral array and its co-array

图5(a)显示了圆形阵列在长方形口径内的布局，可以看到左右两侧存在明显的空白区域，对空间的利用不够充分；而图5(b)中的椭圆形阵列布局非常适合长方形区域，阵元在空间内的分布较为均匀。

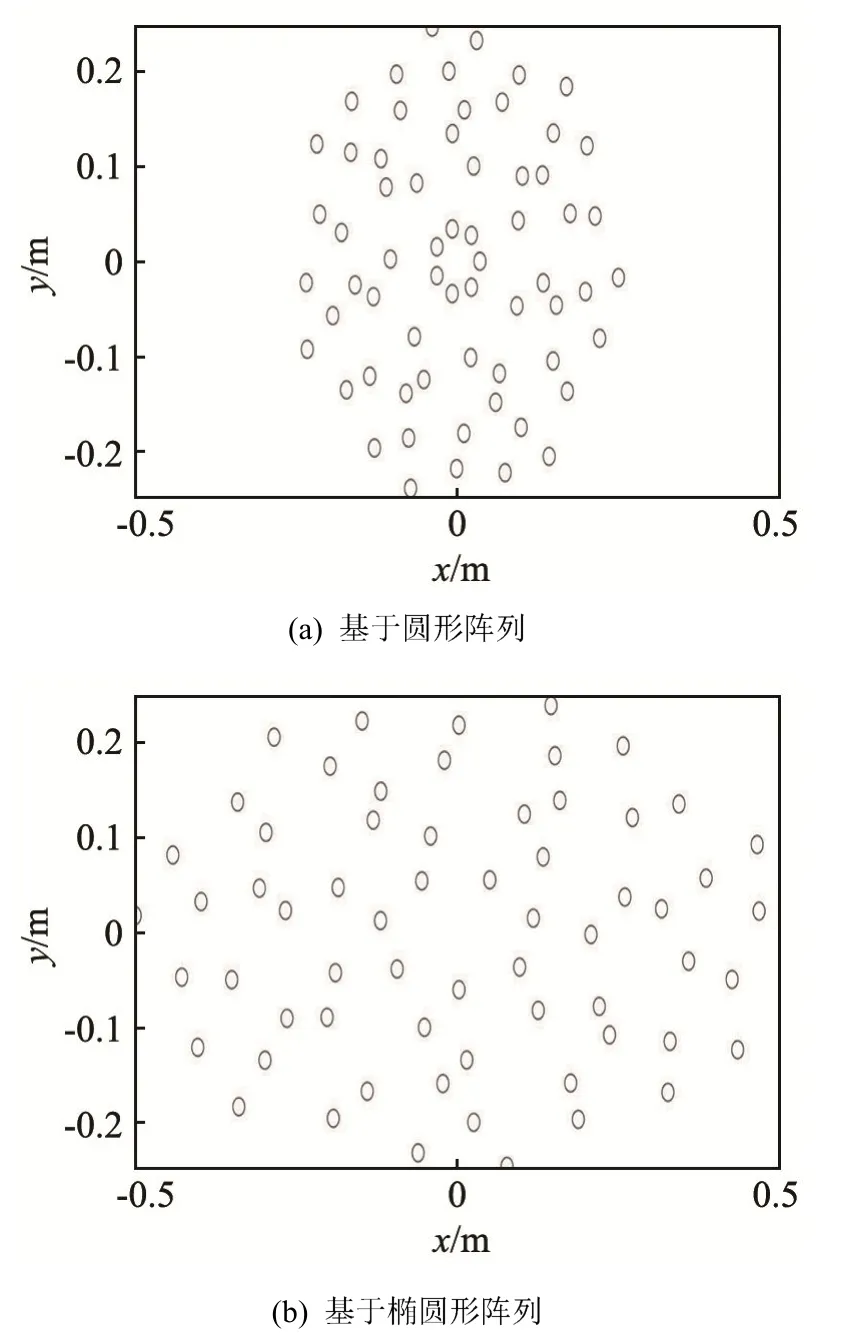
图5 在长方形区域内布置阵元Fig.5 Arrangement of array elements in a rectangular area

假设在风洞长方形开口上方左侧存在一个单极子，坐标为右侧存在一个偶极子，坐标为点声源的频率均为3 kHz。两种阵列布局方式对于点声源的波束形成结果如图6所示，图6(a)和 6(b)分别对应于圆形和椭圆形阵列。扫描平面距阵列平面0.7 m，扫描范围2 m×1 m，从点声源成像结果中可以看到：圆形阵列在口径中间位置的空间采样较高，旁瓣峰值及平均水平略低于椭圆形阵列，但椭圆形阵列的分辨率要明显高于圆形阵列，约为3倍。综合以上两个指标，在风洞壁面长方形开口的限制下，基于椭圆的阵列成像结果要优于基于圆形的阵列成像结果。

3.3 “窗口”型阵列

“窗口”型阵列有更广的适用范围，假设风洞壁面某个区域内开有若干开口，每个开口面积不足够大，不适合单独布置阵列，如图7(a)中的三个矩形所示，此时可将所有开口综合考虑，进行“窗口”型阵列布置。其设计步骤如下：

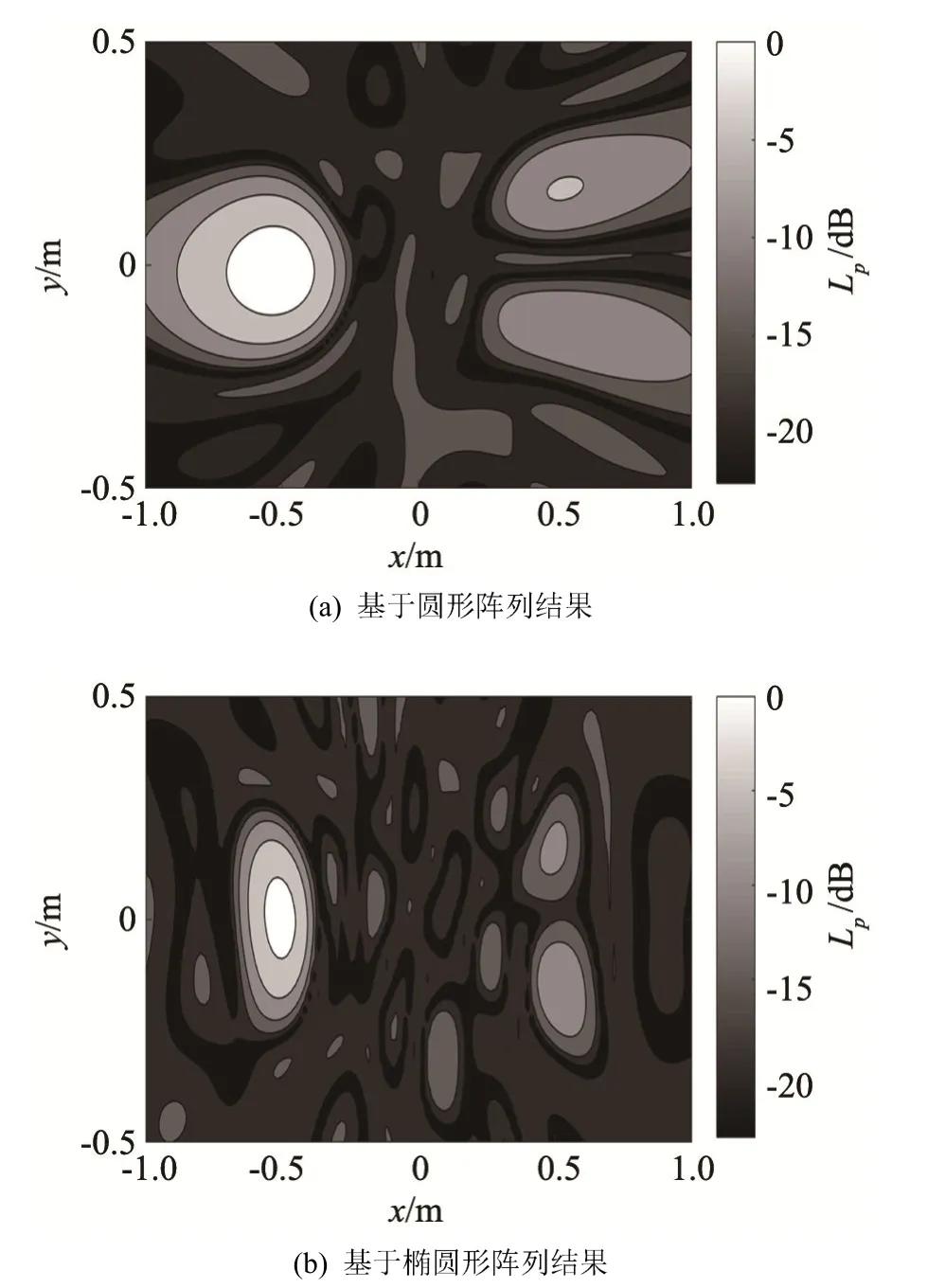
图6 基于圆形阵列和基于椭圆形阵列的成像结果对比Fig.6 Comparison of imaging results between circle and ellipse based arrays

(1) 将最外侧矩形所包围的区域视为一个整体，在其中进行多臂螺旋线阵列布置，并尽可能地充分利用空间，满足空间采样需求；

(2) 仅保留三个矩形内部的阵元，将处于外侧矩形和三个矩形之间的阵元去掉，图7(a)共去掉了21个阵元；

(3) 剩余42个阵元满足阵列最优设计准则，将其作为整体对模型进行声学测量。

“窗口”型阵列对于3 kHz单极子的波束形成结果如图7(b)所示，与无“窗口”63阵元的结果(见图3(a))相比，旁瓣的数量、峰值和平均水平都明显增加，主瓣的分辨率略有提高。发生变化的原因在于：在设计布置 63个声传感器阵列的口径内仅布置了42个阵元，而且去掉阵元的区域靠近阵列中间位置，使得剩余的阵元布置相对靠外，去掉声传感器的区域空间采样率变低，所以靠近阵列口径中央位置的声源分辨率有所提高。需要指出的是，“窗口”型阵列布局方法可推广到风洞壁面其它不规则的开口，比如弧形开口等。

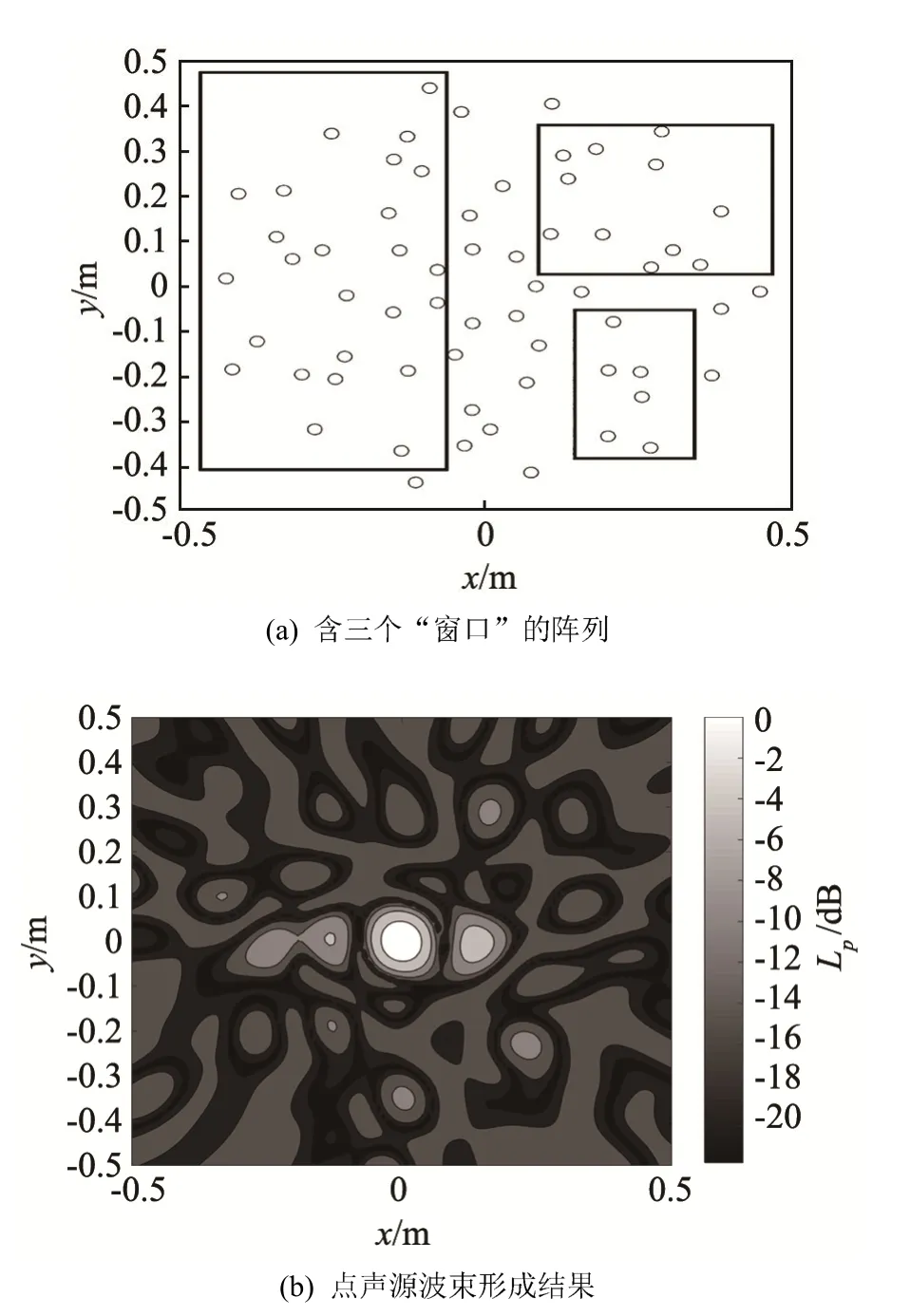
图7 窗口型阵列设计及成像结果Fig.7 Window typed array design and its imaging results

4 实验验证

为了验证所设计阵列的有效性，在闭口风洞中进行了如图8所示的风洞噪声测量实验。其中模型襟翼高度距离阵列平面为1.4 m，襟翼角度为20°，模型攻角为 10°。在模型正下方的长方区域内布置有基于椭圆多臂螺旋线分布的声传感器阵列，阵列通道数为56，目的是测量在不同风速条件下，模型上噪声的分布情况。

图8 椭圆形阵列成像实验Fig.8 Array imaging experiment based on ellipse

图9给出了在频率为 4 kHz、风速分别为 30 m.s-1和50 m.s-1时噪声分布的波束形成结果。从图9中可以很清晰地看出噪声的具体分布，随着风速的增加，噪声的声压级显著提高，旁瓣数量和旁瓣水平也明显增加。但在风速增加的过程中，信号源成像的主瓣并没有发生明显变形，这是由于阵列在模型所在空间采样较为均匀的原因，同时也证明了基于椭圆的阵列设计非常适合长方形开口。

图9 风洞实验成像结果对比(频率4 kHz，距离阵列平面1.4 m)Fig.9 Comparison of imaging results in wind tunnel experiment

5 结 论

阵列通过对模型扫描获得气动声源的位置信息，在阵列布局受限的条件下，阵列设计成适合声源分布时才能得到最佳的成像结果。本文提出了三种针对闭口风洞声学测量的二维阵列设计方法，基本上满足了实际的测量需求，通过分析可以得到以下结论：

(1) 阵列设计在满足最优准则前提下，要考虑三个指标：分辨率、指向性和对旁瓣的抑制能力，这三个指标不会同时达到最优，要根据测量对象和测量需求做出权衡。

(2) 阵元的布局影响空间采样率，在声源分布未知的情况下，阵元要尽可能利用阵列口径内空间，均匀布置，避免区域之间的空间采样率差别过大，影响测量结果。

(3) 影响阵列成像的因素有：声传感器布置、通道数量、阵列口径、疏密分布、背景噪声、通道噪声等，在阵列设计过程中要对所有因素进行综合考虑，尽量以最小代价获得最优结果。

(4) 满足最优设计准则的阵列没有绝对好坏，只存在是否与测量对象相匹配的问题，要根据测量对象和风洞实际及时调整，以达到最佳效果。

参考文献

[1] PAGANIJR C C, SOUZA D S, MEDEIROS M A F. Slat noise:aeroacoustic beamforming in closed-section wind tunnel with numerical comparison[J]. Aiaa Journal, 2016, 54(7): 1-16.

[2] 季建朝, 张宇, 王明新. 声传感器阵列风洞测量结果优化[J]. 清华大学学报(自然科学版), 2018, 58(1): 94-100.JI Jianchao, ZHANG Yu, WANG Mingxin. Optimization of acoustic sensor arrays for wind tunnel measurements. Journal of Tsinghua University(Science and Technology), 2018, 58(1): 94-100.

[3] MUELLER T J. Aeroacoustic Measurements[M]. Berlin Heidelberg: Springer, 2002.

[4] 黄奔. 气动噪声源的麦克风阵列识别定位技术研究[D]. 绵阳: 中国空气动力研究与发展中心, 2014.HUANG Ben. Investigation of aerodynamic noise sources identification technique based on microphone arrays[D]. Mianyang:China Aerodynamics Research and Development Center, 2014.

[5] 冯志国. 麦克风阵列优化设计中的算法与理论分析[M]. 重庆: 重庆大学出版社, 2015.FENG Zhiguo. Algorithms and theoretical analysis in microphone array optimization design[M]. Chongqing: Chongqing University Press, 2015.

[6] 曹虎林. 基于麦克风阵列的声源定位系统硬件设计与算法研究[D]. 上海: 上海交通大学, 2011.CAO Hulin. Algorithm research and hardware design of source localization system based on microphone array[D]. Shanghai:Shanghai Jiao tong University, 2011.

[7] 周家检, 郝璇, 张卫民, 等. 相阵列技术在民机机体气动噪声研究中的应用[J]. 空气动力学学报, 2016, 34(1): 91-97.ZHOU Jiajian, HAO Xuan, ZHANG Weimin, et al. Application of phased array technique in the research of civil airplane airframe noise[J]. Acta Aerodynamica Sinica, 2016, 34(1): 91-97.

[8] FENECH B A. Accurate aeroacoustic measurements in closed-section hard-walled wind tunnels[D]. University of Southampton, 2009.

[9] 张强. 气动声学基础[M]. 北京: 国防工业出版社, 2012: 94-95.ZHANG Qiang. Aerodynamic fundamentals[M]. Beijing: National Defence Industry Press, 2012: 94-95.

[10] 季建朝, 白龙, 黄迅. 基于状态观测器的波束形成算法及其航空应用[J]. 航空学报, 2011, 32(1): 35-40.JI Jianchao, BAI Long, HUANG Xun. A state observer based algorithm for aeroacoustic beamforming[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 35-40.

[11] HUANG J, ZHANG X, GUO F, et al. Design of an acoustic target classification system based on small-aperture microphone array[J].IEEE Transactions on Instrumentation & Measurement, 2015,64(7): 2035-2043.