超声波流量计换能器系统理论分析及应用

夏金东，黄海宁，张春华

(1. 中国科学院声学研究所，北京100190；2. 中国科学院大学，北京100049)

0 引 言

超声波技术是一项多学科交叉、快速发展的高新技术[1-4]，在工业生产和科学研究中有着广泛的应用。超声波流量计就是超声波技术的一项具体应用，在监测、控制和测量领域有着重要的地位。随着近年来微电子技术和智能算法的发展，超声流量测量也得到了快速的发展，流量测量的精度和测量的实时性都得到了提高，智能化、高精度、小流量测量是超声波计量研究的热点之一[5-11]。

超声波流量计利用超声波信号检测流量的方法主要有以下几种[12-13]：传输速度差法(包括时差法、频差法和相差法)、相关法、多普勒法、波束偏移法、管道兰姆波法等。传输速度差法是管道流量测量中最流行的方法，它根据超声波在流体介质中顺流和逆流的速度不同，检测出在固定距离内顺流和逆流的时间差或频率差，从而可以求出流体的速度，已知流速就可得到流经一定面积的流量。

所有的超声波流量测量方法都基于超声波的产生、传播和接收。因此，超声波换能器作为产生和接收超声波信号的器件在超声流量测量系统中起着关键的作用。超声波换能器在流量计中通常成对使用，依照设定的频率，一个发射超声波，另一个接收超声波，然后发射方和接收方再互换，完成一次测量。然而，对于同一个超声波换能器来讲，最大发射电压灵敏度和最大接收电压灵敏度通常不在同一个频率点上。为了在超声波流量测量系统工作频率上获得最优的超声波信号，换能器系统必须优化设计并采用合适的材料，按照合适的工艺进行制作。

本文通过对超声波流量计换能器系统的理论分析，提出了一种最优超声波换能器的设计方法，在此基础上给出了换能器的设计准则，依照此设计方法和准则，设计并研制了超声波热量表换能器，并对换能器进行了实用测试。试验取得了良好的效果，同时验证了设计理论的正确性，证明了按照此设计理论和准则设计的超声波换能器能够为超声波流量测量系统提供最优的超声波信号(幅值最大，波形最佳)。

1 超声波换能器系统的工作机理

超声波换能器在流量计中通常是成对使用的，将两个超声波换能器安装在固定位置，流体从换能器形成的声路径中通过，由于流速的影响导致超声波通过两个换能器形成的声径的时间或频率发生变化。通过测量这种变化，可以得出流体的速度，进而由面积积分获得流量。传播速度差法流量计成对使用的换能器工作原理如图1所示。

流体以速度V流过发射和接收两个换能器形成的声径，当底端的换能器1发射声波而顶端的换能器2接收声波时，此时为顺流时间T上，当顶端的换能器2发射声波而底端的换能器1接收声波时，此时为逆流时间T下，通过测量时间或频率的差值并利用推导公式可以得出流体速度V，最后进行积分获得流量[6]。

成对使用的换能器即是发射换能器，又是接收换能器。因此，为了从每个换能器中获得最佳的超声波信号，两个换能器在理论上应当是完全一样的。表征单独使用的换能器或基阵性能的参数有：工作频率、发射电压响应、接收电压灵敏度、指向性等。但是，几乎没有表征成对使用的换能器系统的性能参数。因此，必须有一个参数来表征成对使用的换能器系统的性能，并由此来指导换能器的设计，才能使换能器系统的性能最优，也就是换能器系统能为整个流量测量提供最优的超声波信号。

1.1 收发电压灵敏度

流量计中的超声波在流体或气体中传播，因此可以借鉴水声换能器参数来表征超声波换能器。水声换能器参数中最重要的就是电压灵敏度，这里用收发电压灵敏度来表征换能器系统的电压灵敏度。收发电压灵敏度定义为成对换能器在相距1 m时，在某种理想的无衰减的声介质中，发射换能器每伏电压下发射的声波在接收换能器上产生的电压。

根据水声换能器表征参数的定义[14-16]，发射电压响应(Transmitting Voltage Response，TVR)表示为

其中是超声波换能器在距离1 m处每伏电压产生的声压，为参考声压，

接收电压灵敏度(Receiving Voltage Sensitivity，RVS)表示为

其中，是1 µPa声压在接收换能器上产生的电压，Uref是参考电压，

合并公式(1)和(2)，可以得出流体中发射换能器在1 V电压下发射的声波在1 m处接收换能器得到的电压，也即成对换能器的收发电压灵敏度(Tranceiving Voltage Sensitivity，TVS)可表示为

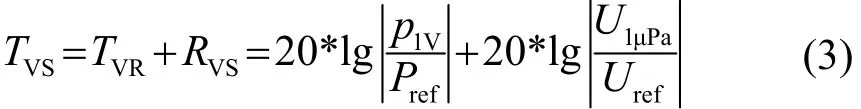
收发电压灵敏度也可以等效成二端口网络的传输响应，两个换能器分别看作是输入和输出端口，声传播介质可看作是能量耦合剂。收发电压灵敏度是成对换能器发射和接收性能的综合表征，这个参数是成对换能器性能的重要表征参数。例如，换能器A和换能器B组成换能器对时，换能器A发射声波而换能器 B接收声波，收发电压灵敏度表示了换能器A发射、B接收的性能。

1.2 平均收发电压灵敏度

平均收发电压灵敏度(Mean Tranceiving Voltage Sensitivity，MTVS)表示的是成对换能器系统的平均收发电压灵敏度，是的平均值，这个参数反映了系统的总体性能。平均收发电压灵敏度可表示为

1.3 收发电压灵敏度差

通常成对换能器的收发电压灵敏度不是完全相等的，收发电压灵敏度差(Difference Tranceiving Voltage Sensitivity，DTVS)反应了成对换能器收发电压灵敏度之间的差异，用两个收发电压灵敏度差的绝对值表示：

1.4 最大收发电压灵敏度频率

成对换能器的收发电压灵敏度也是频率的函数，因此在换能器的工作频率内存在最大、最小值。最大收发电压灵敏度对应的频率对整个超声流量系统来讲是重要的参数，这个频率应该与测量系统的工作频率一致、在保证值最小的情况下使得值最大以及换能器对波束宽度具有很好的一致性，在这种情况下换能器对才能提供最佳的超声波信号。

除了单个换能器的阻抗、指向性外，成对超声波换能器上面的这些参数也是十分重要的。下面基于这些参数，设计了超声波压电换能器系统，并进行特征分析，然后对超声流量测量系统进行了优化设计。

2 超声波换能器系统的设计

超声波流量计的工作频率通常大于1 MHz，以便能够获得更高的测量精度。压电超声波换能器由于具有很多优点而被广泛应用。压电陶瓷是应用最多的压电材料，有许多优点，如：成本低、压电性能高、种类多、机械强度高、容易成形、性能稳定、工艺成熟等。

基于以上超声换能器的设计理论，采用压电陶瓷材料设计流量计的工作频率为 1 MHz的超声波换能器。1 MHz的超声波换能器通常有一个小的辐射面产生宽的波束。波束宽度和圆辐射面的关系表达式为[14]

其中：λ是工作频率下超声波在流体中传播时的波长；D是辐射面的直径；Θ-3dB是-3 dB处的波束宽度，如果-3 dB处的波束宽度为6°，那么圆辐射面的直径大约是14.5 mm。这种换能器一般工作在厚度振动模式，换能器的结构简图[17]如图2所示。

设计换能器的方法主要有有限元法和等效网络法。有限元法是典型的数值仿真方法，给定一组参数值可以得到相应的结果，从大量的计算中可以得到其中的变化规律；而等效网络法能够清晰地表达物理概念并且能进行定量分析。因此，下面采用等效网络方法给出超声波压电换能器的特征分析。

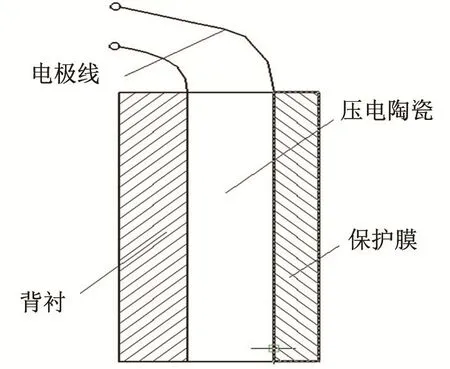
图2 厚度振动换能器的结构简图Fig.2 Schematic diagram of thickness vibration transducer

2.1 发射特性分析

压电陶瓷厚度振动超声波换能器在发射状态下的等效电路图如图3所示。

图3 压电陶瓷厚度振动换能器的发射状态结构简图Fig.3 Equivalent electric circuit model of thickness vibration piezoelectric transducer in transmitting condition

图3中阻抗的表达式为

其中分别表示压电陶瓷、保护膜和后背衬的密度、声速、波数、厚度和面积；n是机电转换系数；C0是静态电容；Zs是辐射阻抗。圆形活塞在无限大障板中的辐射阻抗表示为

其中分别表示传播介质的密度、声速、波数、辐射面积和等效辐射半径；分别表示第一阶贝塞尔函数和斯特鲁函数。

根据等效电路模型，可以计算电导和阻抗曲线，图4和图5分别表示计算的电导和阻抗曲线。给定发射电压Vf施加在换能器上，辐射面的振速uf等效于通过声辐射的电流。因此，当工作频率为f时，声轴方向上远场声压的表达式为

其中，r为远场距离，由此可以得到发射电压响应曲线，计算结果如图6所示。

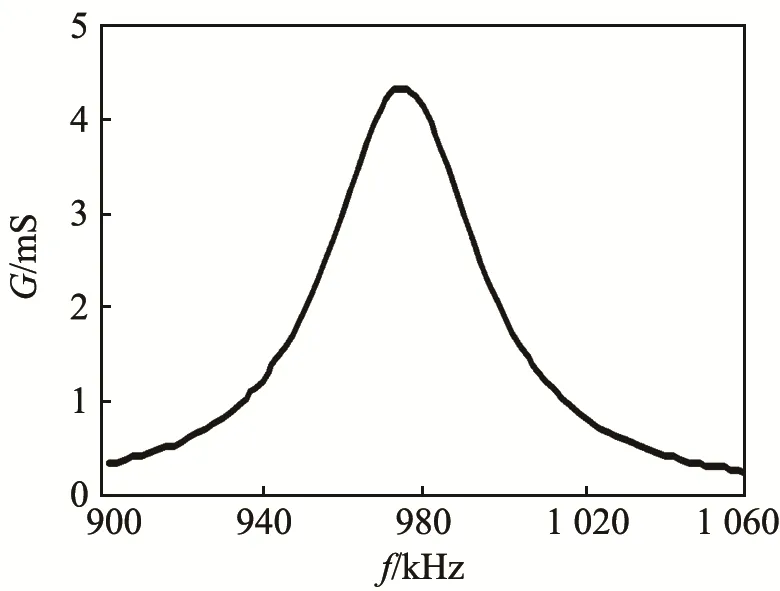
图4 换能器电导计算曲线Fig.4 Calculated conductance curve of transducer.

图5 换能器阻抗计算曲线Fig.5 Calculated impedance curve of transducer.

图6 换能器发射电压响应计算曲线Fig.6 Calculated transmitting voltage response curve of transducer

2.2 接收特性分析

接收状态下厚度振动压电换能器的等效电路如图7所示。

图7 压电陶瓷厚度振动换能器接收状态等效电路图Fig.7 Equivalent electric circuit model of thickness vibration piezoelectric transducer in receiving condition.

声压P在换能器表面上有作用力F，使其产生振动，根据振速和电流的关系，可以得到通过静态电容的电流，由此得到换能器在开路状态下电压的表达式为

因此，接收电压灵敏度表示为

接收电压灵敏度计算曲线如图8所示。

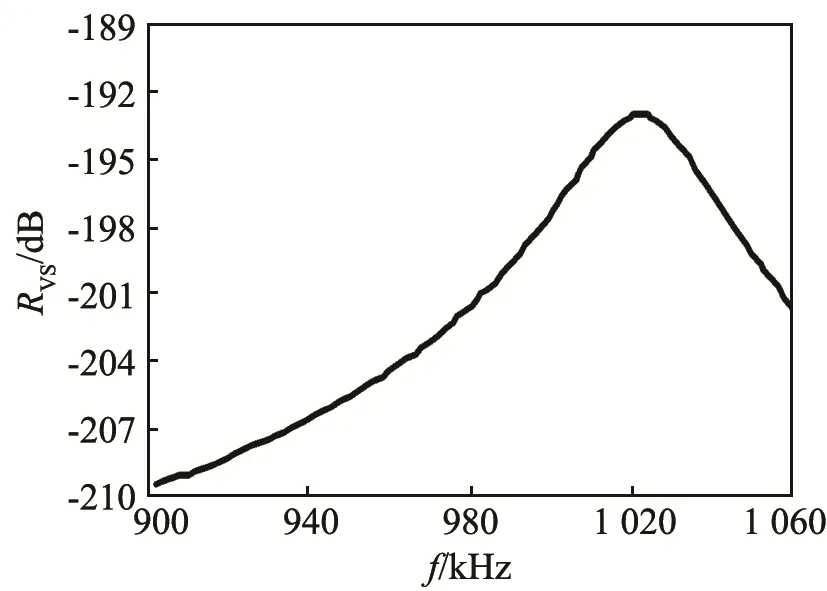
图8 换能器接收电压灵敏度计算曲线Fig.8 Calculated receiving voltage sensitivity curve of transducer.

从图4和图5可以看出，电导的最大值对应的频率与阻抗的最小值对应的频率几乎一致，称为谐振频率，最小电导或最大阻抗对应的频率为反谐振频率；从图5、图6和图8可以看出，在谐振频率处发射电压响应最大，接收灵敏度在反谐振频率处对应的灵敏度最大。

2.3 收发电压灵敏度

超声波换能器发射和接收电压灵敏度的和为收发电压灵敏度，它是表征成对使用的换能器性能的有效参数。图9是压电陶瓷厚度振动换能器的收发电压灵敏度计算曲线，由图9可见，收发电压灵敏度曲线能很好地表示收发换能器系统的工作带宽和最佳工作频率。在最佳工作频率点上，发射、接收换能器系统可以得到最优性能的信号(信号的幅值最高，波形最佳)。

图9 换能器收发电压灵敏度曲线Fig.9 Calculated transceiving voltage sensitivity curve of transducer.

如果超声流量测量系统的工作频率确定，那么换能器系统的设计准则是在该频率上有最大的收发电压灵敏度，且工作带宽、阻抗和波束宽度满足系统要求。

3 超声波热量表换能器试制

根据以上设计，研制了适用于热量表的超声波压电换能器。由于换能器需要长时间浸在水中，而且水温在95℃以上、压力达到4 MPa，因此，对于压电陶瓷、外壳材料及粘接胶都有特殊的要求。压电陶瓷是超声波换能器的关键元件，为了保证换能器在高温下有良好的压电性能，选用高居里温度点的PZT-5压电陶瓷材料，这种材料在100℃时能保持良好的性能。换能器外壳不仅要求有良好的透声性能，而且能耐高温、耐水浸并且具有较高的强度，聚苯硫醚(Polyphenylene Sulfide，PPS)加玻璃纤维材料可以在 180℃下保持良好的性能，耐腐蚀且具有较高的强度，能够满足要求。粘接胶采用120℃固化的、应用于航空的环氧基粘接胶，背衬同样采用耐高温的灌封材料。制作完成后的换能器如图10所示。

在消声水槽中测试了试制的热量表换能器的电导、阻抗、发射电压响应、接收电压灵敏度和指向特性。图11～15是测试结果，测量频率为900～1060 kHz。图11是热量表换能器在水中电导的测量曲线，最大电导的频率在 976 kHz，根据带宽的判断准则，电导的带宽约为54 kHz；图12是热量表换能器的阻抗测试曲线，在测量频率范围内，可以得到谐振频率为 972 kHz和反谐振频率为1027 kHz。

图11 热量表换能器电导测量曲线Fig.11 Measured conductance curve of heatmeter’s transducer

成对热量表换能器的发射电压响应和接收电压灵敏度测量曲线如图13和图14所示。最大发射电压响应在176 dB左右，对应的频率为970 kHz，与电导的谐振频率相近；最大接收电压灵敏度为-192 dB，对应的频率为1020 kHz，与阻抗的反谐振频率相当。图13和图14反映了成对换能器具有良好的一致性。图15是热量表换能器在1 MHz频率时的指向性测试曲线，其-3 dB处的波束开角为6°。在发射电压响应和接收电压灵敏度测量曲线的基础上，得到了成对热量表换能器收发电压灵敏度曲线，如图16所示。从图16中可以看出，热量表换能器对的收发电压灵敏度测试结果具有良好的一致性，最大值为-23 dB，对应的频率为1000 kHz，正是热量表系统的工作频率，在此频率下换能器对为热量表系统提供了最佳信号。根据带宽判断准则，换能器对的工作带宽约为65 kHz，满足系统的带宽需求。通过分析计算，换能器对在频率为1000 kHz时的收发电压灵敏度均值为-22.7 dB，差值为0.6 dB，显示出热量表换能器具有良好的一致性。

图13 热量表换能器发射电压响应测量曲线Fig.13 Measured transmitting voltage response curves of two heameter’s transducers

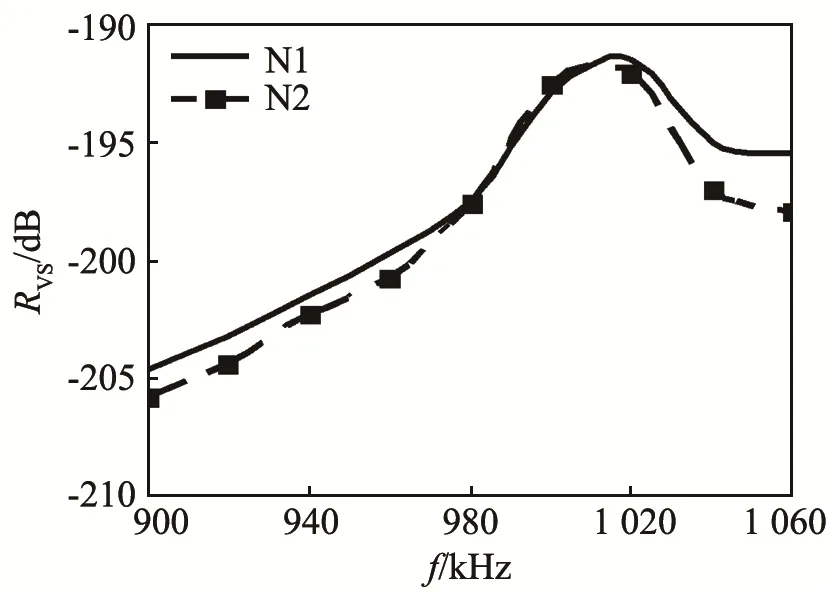
图14 热量表换能器接收电压灵敏度测量曲线Fig.14 Measured receiving voltage sensitivity curves of two heatmeter’s transducers

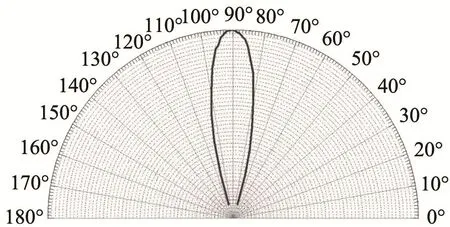
图15 热量表换能器1 MHz指向性测量曲线Fig.15 Measured directivity of heatmeter’s transducer at 1 MHz

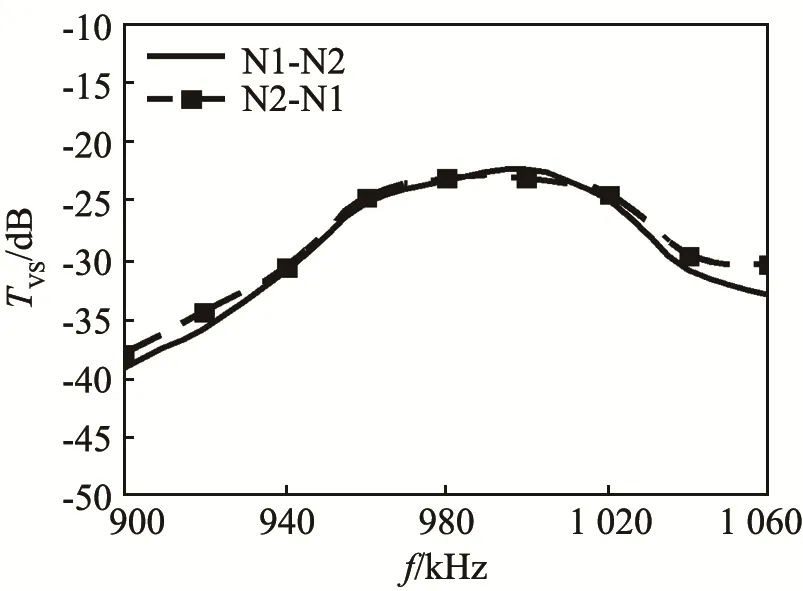
图16 两种热量表换能器组合的收发电压灵敏度曲线Fig.16 Tranceiving voltage sensitivity curves of two heatmeter’s transducer combinations

为了在实际工作条件下验证热量表换能器的性能，成对换能器安装在热量表管段中，90℃以上的热水从管道中流过，分别测试成对换能器的发射和接收性能。实验装置如图17所示，图18是一个换能器发射，另一个换能器接收的信号，图19是原来用作接收的换能器发射信号，原来用作发射的换能器接收信号，驱动电压均为3.02 V，接收信号的电压分别为2.93 V和2.89 V，幅值非常接近，波形良好无畸变，实验结果很好地验证了理论分析的正确性。

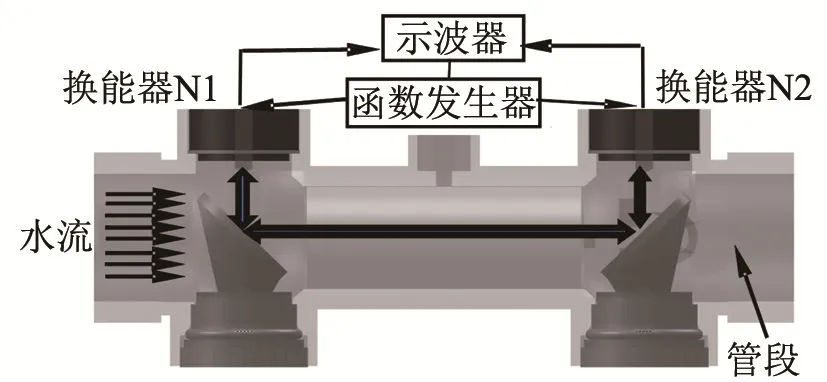
图17 热量表换能器管道安装测试图Fig.17 Schematic diagram of pipe installation test for heatmeter’s transducers

图18 热量表换能器N1发射、N2接收的信号Fig.18 Measured signal in the case of transducer N1 transmitting and transducer N2 receiving

图19 热量表换能器N2发射、N1接收的信号Fig.19 Measured signal in the case of transducer N2 transmitting and transducer N1 receiving

4 结 论

为使换能器能为超声流量测量系统提供最优的信号，提出了成对超声波换能器的设计方法和准则，通过分析换能器的电导、阻抗、发射和接收特性及相互关系，采用换能器之间的收发电压灵敏度作为表征换能器成对使用时的综合性能参数。应用此参数可以设计出满足测量系统要求的超声波换能器，换能器的谐振频率要低于最大收发电压灵敏度对应的频率即系统的工作频率。

在最大收发电压灵敏度对应的频率上，成对使用的换能器能提供最佳信号(幅值最大、波形无畸变)，因此，把收发电压灵敏度作为衡量成对使用换能器的一个综合评价指标。成对使用的换能器其收发电压灵敏度在理论上是完全一致的，但在实际中需要根据测试系统的要求制定出最小的收发电压灵敏度并以此作为挑选换能器的一个指标。最后通过热量表换能器的试制、测试和实验，证明了设计理论及方法的正确性，可以应用于超声波流量测量系统的换能器设计。

参考文献

[1] LYNNWORTH L C, LIU Y. Ultrasonic flowmeters: Half-century progress report, 1955-2005[J]. Ultrasonics, 2006,44(1): 1371-1378.

[2] TABIN J. Theoretical analysis of the ultrasonic doppler flowmeter for measurements of high flow velocities[J]. IEEE Transaction on Ultrasonic Ferroelectrics and Frequency Control, 1987, 34(4):467-471.

[3] SANDERSON M L, YEUNG H. Guidelines for the use of ultrasonic non-invasive metering techniques[J]. Flow Measurement and Instrumentation, 2002, 13(4): 125-142.

[4] JAKIRLIC S, HANJALIC K, TROPEA C. Modeling rotating and swirling turbulent flows: A perpetual challenge[J]. AIAA Journal,2002, 40(10): 1984-1996.

[5] HE C, LIU F, ZHANG L, et al. Adaptability study of multi-path ultrasonic flowmeter installed in a bend pipe[J]. Chinese Journal of Scientific Instrument, 2011, 32(1): 6-12.

[6] YEH T T, ESPINA P I, OSELLA S A. An intelligent ultrasonic flow meter for improved flow measurement and flow calibration facility[J]. IEEE Transactions on Instrumentation and Measurement, 2001, 3(3): 1741-1746.

[7] ZHAO H, PENG L, TAKAHASHI T, et al. Support vector regression-based data integration method for multipath ultrasonic flowmeter[J]. IEEE Transaction on Instrumentation and Measurement,2014, 63(12): 2717-2725.

[8] CHEN G Y, LIU G X, ZHU B G, et al. 3D isosceles triangular Path of Transit-Time ultrasonic flowmeter: theoretical design and CFD simulations[J]. IEEE Sensors Journal, 2015, 15(9): 4733-4742.

[9] WADA S, TEZUKA K, TREENUSON W, et al. Study on the optimal number of transducers for pipe flow rate measurement downstream of a single elbow using the ultrasonic velocity profile method[J]. Science and Technology of Nuclear Installations, 2012:1-12.

[10] RUPPEL C, PETERS F. Effects of upstream installations on the reading of an ultrasonic flowmeter[J]. Flow Measurement and Instrumentation, 2004, 15(3): 167–177.

[11] AMRI K, WIRANATA L F, et al. Fluid flow velocity measurement using dual-ultrasonic transducer by means of simultaneously transit time method[C]//Proceedings of the 4th International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering (ICICI-BME), 2015: 113-116.

[12] MANDARD E, KOUAMÉ D, BATTAULT R, et al. Transit time ultrasonic flowmeter: Velocity profile estimation[C]//IEEE Ultrason. Symp. Proc., 2005: 763-766.

[13] MOORE P I, BROWN G J, et al. Ultrasonic transit-time flowmeters modelled with theoretical velocity profiles: Methodology[J].Measurement Science and Technology, 2000, 11(12): 1802-1811.

[14] SHERMAN C H, BUTLER J L. Transducers and arrays for underwater sound[M]. New York: Springer, 2007.

[15] LURTON X. An introduction to underwater acoustics[M]. New York: Springer, 2010.

[16] 中华人民共和国国家质量监督检验检疫总局. GB/T 7965—2002声学 水声换能器测量[S]. 北京: 中国标准出版物社, 2002.The General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. GB/T 7965-2002 Acoustics-Measurement of underwater sound transducers[S].Beijing: China Standard Press, 2002.

[17] 栾桂冬, 张金铎, 王仁乾. 压电换能器和换能器阵[M]. 北京: 北京大学出版社, 2005.LUAN Guidong, ZHANG Jinduo, WANG Renqian. Piezoelectric transducers and arrays[M]. Beijing: Peking University Press, 2005.