变幅杆弯曲振动频率的计算及分析

蒙永红，贺西平，崔晓娟，卫相润

（陕西师范大学物理学与信息技术学院，陕西省超声重点实验室，陕西西安710119）

变幅杆的主要作用是聚能和机械阻抗匹配。林仲茂对传统的纵向振动变幅杆做了详细的研究[1]。文献[2]提出了一端输入、多端输出的纵振动转换体，根据连接处各物理量的连续条件推导出了设计转换体的频率方程。文献[3]推导了夹角型变幅杆的矩阵解析法。超声变幅杆纵向振动时会不可避免地出现弯曲振动，影响振动系统的稳定性,也会降低振动系统的工作效率，严重时会出现啸振甚至停振。

有目的地利用弯曲振动有利于超声加工。例如，对蓝宝石衬底进行辅助化学机械抛光加工，使其表面光滑，提高材料去除率[4]；双向弯曲振动对硬脆材料以椭圆振动的方式进行加工，可得深度为1.9 μm的小槽[5]；弯曲振动的焊极利于塑料焊接[6]。为了研究变幅杆的弯曲振动，文献[7]、[8]用传输矩阵法计算了超声锥形变幅杆的弯曲振动频率。文献[9]提出了变截面杆弯曲振动的半解析法。文献[10]计算了一种圆锥形变幅杆弯曲振动固有频率。

本文以圆柱型变幅杆为例，分别在只考虑转动惯量或只考虑剪切形变影响时采用Euler-Bernoulli理论以及在考虑转动惯量和剪切变形影响时采用Timoshenko理论，计算了该变幅杆的弯曲振动频率方程，并得到了杆的前三阶频率值，又利用有限元软件计算其弯振频率，将解析计算和有限元计算结果与实验测试值进行了比较。

1 圆柱型变幅杆弯曲振动固有频率

等截面杆弯曲自由振动的微分方程为：

式中：I为转动惯量；Y为横向位移；K′为剪切系，对于圆截面取值为0.9；A为截面圆的面积。

1.1 Euler-Bernoulli理论

式（1）中若不考虑转动和剪切，所得均匀截面杆的弯曲振动方程为：

式中：Y为杆上各点的横向位移；c为纵波声速；截面的回转半径K为半径r的一半。

结合自由边界条件可得：

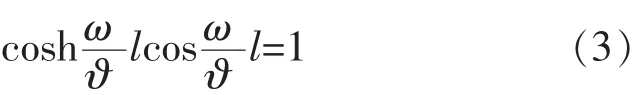
则两端自由的圆柱型杆弯曲振动谐振频率方程为：

式中：

1.2 考虑转动惯量的弯曲振动频率

在只考虑转动惯量的影响时，式（1）中不含剪切系数，则弯曲振动方程为：

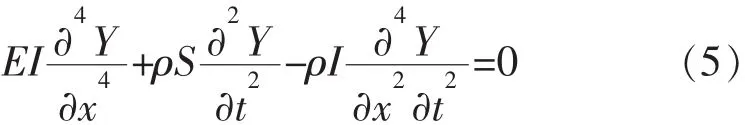
令 Y（x，t）=y（x）T（t），则杆两端自由边界条件下的弯曲振动谐振频率方程为：

1.3 考虑剪切变形的弯曲振动频率

在只考虑弯曲变形引起的剪切效应时，式（1）中不含项，则弯曲振动方程为：

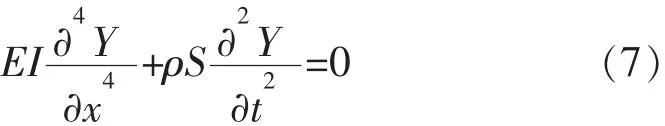
令 Y（x，t）=y（x）T（t），同理可得弯曲振动谐振频率方程为：

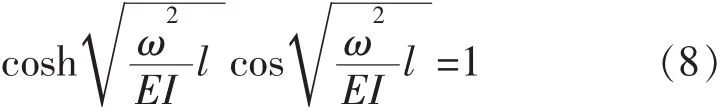
1.4 考虑转动惯量和剪切变形影响的Timoshenko理论

简化式（1），可得Timoshenko理论杆的弯曲振动方程为：

由此可得弯曲振动谐振频率方程为：

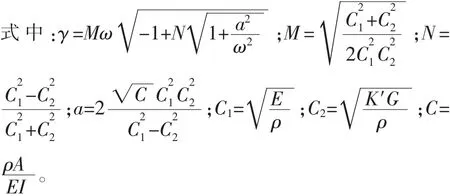
2 有限元计算

取一圆柱型变幅杆，其截面直径D=15 mm，长度L=120 mm，材料为45钢，杨氏模量E=2.10e11Pa，剪切模量G=8.0e10Pa，密度ρ=7800 kg/m3。如图 1所示，采用Ansys15.0软件建立杆的有限元模型，其坐标原点位于x=0处，所建模型单元类型为Solid187，其中单元数和节点数分别为22 978和4694。图2a～图2c分别为弯曲振动的前三阶振型图。

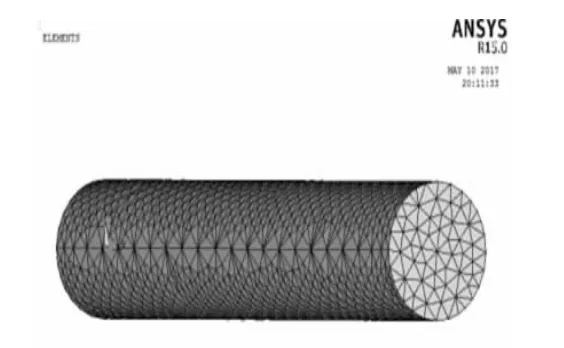
图1 圆柱形变幅杆的有限元模型

3 实验测试及分析

为了验证上述理论计算方法，通过实验测试了该圆柱形变幅杆两端自由状态的弯曲振动频率，测试结果见图3。实验采用VibPilot振动测试系统多通道测试仪器，将交变信号的电压和频率施加到厚度为0.4 mm、直径为10 mm的压电陶瓷片上。利用YD-8型加速度计采集这种振动，并将采集的信号传回VibPilot系统，经分析、处理后得到测试结果。

图3 变幅杆两端自由状态的弯曲振动频率测试结果

加工上述尺寸的变幅杆，由式（4）、式（6）、式（8）和式（10），即可求得该变幅杆的前三阶弯曲振动频率，结果见表 1。 其中，下标 E、B、S、T、e、t分别表示：Euler-Bernoulli理论计算值、考虑转动惯量的理论计算值、考虑剪切变形的理论计算值、Timoshenko理论计算值、有限元计算值、实验测试值。上述各方法与实验测试值的误差分别为：Δ1=

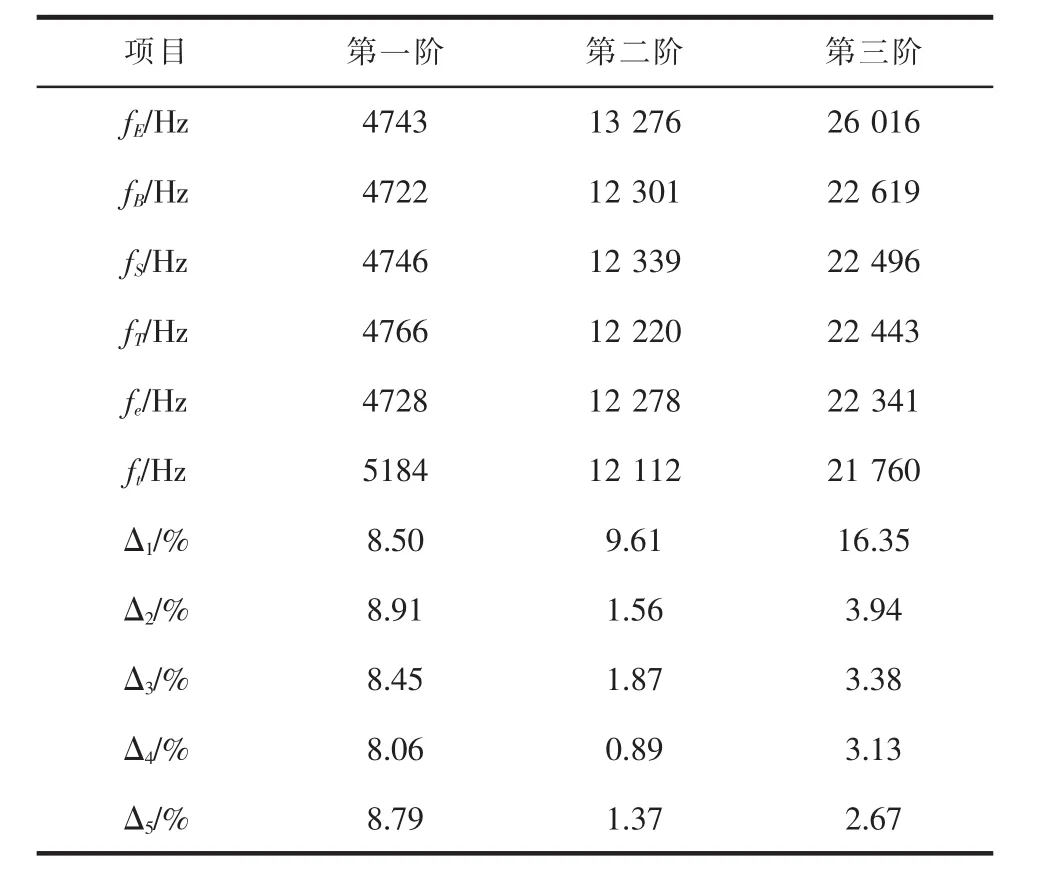
表1 变幅杆前三阶弯曲振动频率的理论计算与实测值

由表1可知，Euler-Bernoulli理论计算结果与实验测试结果相比误差较大；有限元计算结果误差为1.37%～8.79%。Timoshenko理论计算结果与实验测试结果最接近，其最大误差只有8.06%，最小误差为0.89%。这是因为Euler-Bernoulli理论忽略了变幅杆的转动惯量和剪切变形影响，故造成的误差较大；而Timoshenko理论考虑了这两种情形，使其理论值与实验测试值较接近。

4 结束语

本文利用Euler-Bernoulli和Timoshenko理论，计算、实测了圆柱型变幅杆的弯曲振动频率，发现Timoshenko理论的计算结果与实验测试结果最接近。基于该方法，可研究变截面变幅杆的弯曲振动频率，为纵-弯耦合、弯-弯耦合等复合型振动系统的设计提供理论依据。

参考文献：

[1]林仲茂.超声变幅杆的原理和设计[M].北京：科学出版社，1987.

[2]贺西平，张海岛.单端输入多端输出的纵振动转换体的研究[J].中国科学：物理学 力学 天文学，2016，46（3）：034301.

[3]张海岛，贺西平，王维鸽.夹角型变幅杆的矩阵解析法[J].云南大学学报（自然科学版），2016，38（2）：225-231.

[4]XU Wenhu，LU Xinchun，PAN Guoshun，et al．Ultrasonic flexural vibration assisted chemical mechanical polishing forsapphire substrat [J]．Applied Surface Science，2010，256（12）：3936-3940．

[5]SUZUKI N，MASUDA S，HARITANI M，et al．Ultraprecision micromachining of brittle materials by applying ultrasonic elliptical vibration cutting[C]//Micro-Nanomechatronics and Human Science，2004 and the Fourth Symposium Micro -Nanomechatronics for Information-Based Society，2004．Nagoya，2004：133-138．

[6]WATANABE Y，MORI E.A study on a new flexuralmode transducer-solid horn system and its application to ultrasonic plastics welding[J].Ultrasonics，1996，34 （2-5）：235-238.

[7]周光平，李明轩.超声弯曲模式变幅杆的振动分析[J].声学学报，2000，25（2）：120-125.

[8]ZHOU Guangping，LI Mingxuan.A study on ultrasonic solid horns for flexural mode[J].Journal of Acoustical Society of American，2000，107（3）：1358-1362.

[9]崔灿，蒋晗，李映辉.变截面梁横向振动特性半解析法[J].振动与冲击，2012，31（14）：85-88.

[10]严日明，刘德福，陈涛，等.一种圆锥形变幅杆弯曲振动固有频率的计算方法 [J].振动与冲击，2016，35（7）：198-204.