齿轮齿面超声挤压强化有限元模拟
2018-05-18赵慧玲张勤俭房善想
赵慧玲,张勤俭,房善想
(北京交通大学机械与电子控制工程学院,北京100044)
随着我国科学技术飞跃发展,各行各业对齿轮的强度和表面质量提出了更高的要求,尤其是我国高速列车、工程机械及航空航天技术的飞速发展,对于齿轮特别是高速重载齿轮综合性能的要求日益提高。传统的齿轮表面强化工艺主要有渗碳渗氮、涂层强化、喷丸、激光淬火等方法,近年来,还出现了超声喷丸等强化方法。传统的强化方法虽然在一定程度上改善了齿轮表面的性能,但仍无法彻底解决齿轮疲劳破坏问题。
随着超声波技术的发展,超声挤压强化技术在表面强化领域显示出了独特的优势。当前,我国学者已在超声挤压强化技术方面取得了一定的研究成果,并在生产实践中得到了应用。例如:对板料、棒料等规则表面进行超声强化处理后,材料表面可产生残余应力,且硬化层深度明显增加,表面粗糙度值可低于Ra0.1 μm,疲劳强度得到显著提高。然而,超声挤压技术在齿轮表面强化方面的相关研究还很少,尚有较大的研究空间。本文应用有限元方法将超声挤压强化技术应用于齿轮齿面,提取模拟后的表层残余应力及在不同工艺参数下残余应力随深度变化曲线,分析不同工艺参数对齿轮残余应力的影响。
1 有限元分析前处理
1.1 建立有限元模型
由于齿轮模型及齿轮与工具头接触状态的复杂性,在有限元软件中无法精确地绘制标准的渐开线齿轮模型及装配模型。因此,本文先在SolidWorks软件中建立齿轮和工具头的三维模型及装配体,齿轮的详细参数见表1,并对模型进行简化,不建立其他辅助模型,工具头仅保留和齿面接触的部分,齿轮和工具头以相切的形式接触在一起,其三维模型见图1,然后利用与有限元软件相通的端口导入ABAQUS中进行数值仿真计算。

表1 齿轮参数表

图1 齿轮和工具头装配模型
1.2 选择材料本构模型
模拟时,所选材料需能反映齿轮和工具头的形变特点,故在齿轮齿面超声挤压强化过程中,所选用的齿轮材料为45钢,工具头材料为轴承钢。45钢属于塑性材料,在超声挤压强化过程中,其表层金属的塑性变形、加工硬化和应变率硬化现象较显著。因此,在有限元模拟时需选择一个能合理反映其力学性能的本构模型。
Johnson-Cook(JC)本构模型能综合反映应变、应变率对材料屈服强度的影响,适用于冲击等快速变化过程[1-3]。因此,本文采取JC本构模型,具体可描述为:

式中:为屈服应力;A 为环境温度 Tr(℃)下的初始屈服应力,MPa;B为应变硬化参数,MPa;C为应变率敏感系数;n为应变硬化指数;m为热软化系数。
通过参考相关文献[4],本文所使用的描述45钢塑性变形的JC本构模型见表2。由于超声挤压过程中的温度变化不明显,因此可忽略温度变化产生的软化效应,取T=Tr=20℃。

表2 45钢的JC本构模型参数表
1.3 设置接触类型
齿轮齿面的超声挤压强化是一种高度的非线性行为,在计算过程中,工件的位置、形状会发生变化,接触关系也会随之发生变化,选择合适的接触类型来描述实际的物理系统很难实现,因此,本文在模拟时选择通用接触。
ABAQUS创建接触关系时需选择二个面:主面和从面。一般情况下,主面的刚度比从面大,从面的网格尺寸比主面小[5]。在对齿面进行强化时,工具头是不变形体,所以选择工具头作为主面,齿轮作为从面。根据本文实际的超声挤压强化过程,接触面之间的法向关系选择硬接触,切向关系选择库伦摩擦模型。此外,超声挤压强化过程时温度变化不大,而摩擦系数主要随温度变化,因此可将摩擦系数设定为常值,本文设置切向摩擦系数值为0.1。
1.4 定义载荷与边界条件
在有限元动态模拟分析中,对模型施加合理的载荷及边界条件至关重要。结合本文的实际目的,工具头与齿轮啮合运动的同时做超声振动,从而完成对齿轮齿面的强化,因此可对工具头施加约束,使工具头在z方向的移动自由度保持自由状态,限制其余的五个自由度,从而使工具头只能发生移动。在齿轮安装轴孔中心创建一个参考点RP,通过接触选项中的耦合约束,将该参考点和齿轮的内孔面建立刚性连接,并通过边界条件使该参考点绕齿轮轴线的转动自由度保持自由,其余的五个自由度固定,从而使齿轮只能绕中心轴转动。
超声挤压强化的加载条件为静压力及工具头输出的振幅。但模拟时,在一个自由度上同时施加力和振幅是冲突的,通过查阅文献得知,可利用动态冲击力代替振幅作为初始条件[6],此时载荷为恒定的静压力和动态冲击力,二者均为集中力。在超声挤压强化时,工具头的机械振动所产生的动态冲击力是按正弦函数变化的,在ABAQUS有限元分析中,周期变化的载荷可通过傅里叶函数加载[7]:

式中:A0为初始幅值;n 为谐波个数;an、bn为谐波振幅;w为超声波圆频率。
由于超声振动是正弦波,故取n=1、an=0。静压力可通过初始幅值A0直接定义,动态冲击力通过谐波振幅b1和超声波圆频率w定义,此时载荷为:

1.5 网格划分
采用ABAQUS进行数值模拟时,网格划分非常重要,如果单元类型选择不合理,结果将出现很大的偏差。一般情况下,网格数量越多,计算精度会越高,但网格数量过多会降低计算机的计算效率[8]。用ABAQUS对齿轮强化进行模拟计算时,如果对整个模型进行求解,则需要较多的单元、节点和内存空间,使求解时间过长。因此,在有限元分析中,由于远离接触部位的齿面所受的作用力很小,在综合考虑不影响边界条件定义和计算结果精度的前提下,可将远离接触面的部分绑定为刚体,从而减少计算时间。
对三维模型进行有限元分析时,一般选择六面体单元,其生成的节点较均匀,能有效提高计算的精确性。同时,采用扫略的方法划分网格单元,其精确度较高,较接近理想单元,且对计算机的性能要求较低。因此,本文对齿轮和工具头的网格划分采用扫略网格划分技术,单元类型为C3D8R(八节点六面体实体单元)。这种单元具有大变形能力,可减少计算时间,提高边界条件的拟合性[9]。图2是网格划分后的模型,共划分单元总数为234 000个。
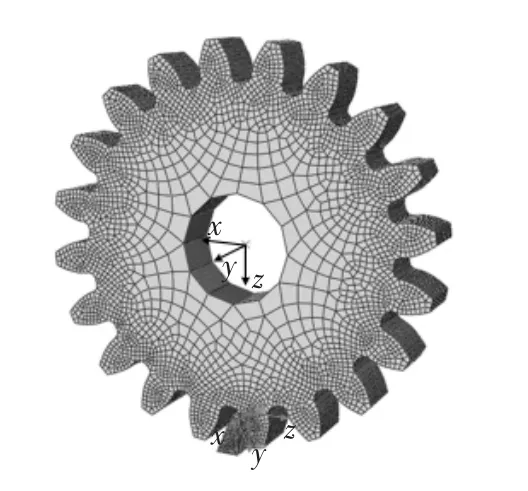
图2 网格划分后的模型
2 有限元结果分析
2.1 超声挤压强化后的齿面残余应力分布
取静压力F=600 N、进给速度v=30 mm/s、振幅A=10 μm、频率f=20 kHz,提取强化后的齿轮齿面的等效应力及各应力分量,如图3所示。

图3 超声挤压强化后的齿面应力分布云图
从图3所示的模拟结果可看出,各应力分量在表面附近表现为压应力,其中,最小主应力绝对值较大,σxx、σyy、σzz、σxy和第二主应力分布较均匀但应力值较小,σxz、σyz和第一主应力接近于零。因此,提取齿轮齿面的最小主应力作为齿面的残余应力。
从图4所示的表面残余应力分布可看出,表面残余应力在360 MPa上下浮动,且为负值,故全部为压应力。因此,采用超声挤压处理材料表面,不会出现因工艺参数不当而使齿轮表面残余拉、压应力处于混合状态的现象。
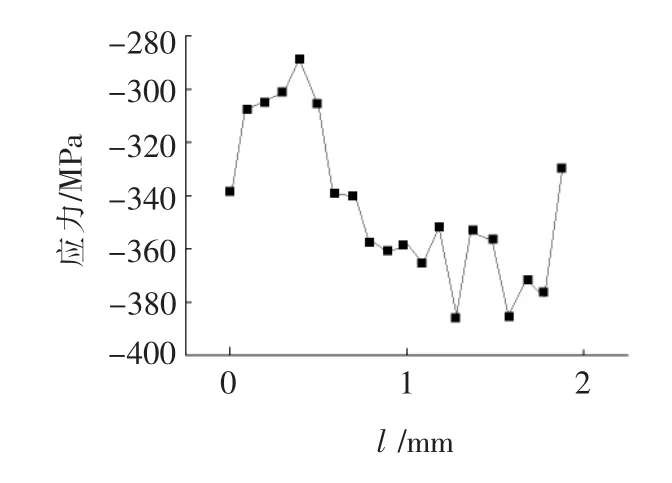
图4 表面残余应力分布图
2.2 静压力对齿面残余应力的影响
取进给速度v=20 mm/s、振幅A=10 μm、频率f=20 kHz,研究不同静压力对残余应力的影响,结果见图5。可见,在齿面表层会产生残余压应力,并会延伸到材料内部,最大值出现在齿面近表层。此外,随着静压力增加,最大残余应力和强化层深度都会增加,且变化程度较大,说明静压力对残余应力的影响至关重要。分析原因:在超声挤压过程中,静压力作为恒定载荷直接作用在齿面上,类似于碾压,使材料内部产生塑性变形,形成残余压应力;增大静压力,可使齿面获得更多的能量,增加塑性变形[10]。因此,可通过适当地增大静压力来提高齿轮表面的残余压应力。

图5 不同静压力下沿深度方向的应力分布图
2.3 进给速度对齿面残余应力的影响
取静压力 F=600 N、振幅 A=10 μm、频率 f=20 kHz,研究不同进给速度对残余应力的影响,结果见图6。可见,随着进给速度增加,最大残余应力和强化层深度都会减小。分析原因:随着进给速度增加,使相邻冲击点的间距增大,单位面积内的冲击密度降低,齿轮表面被冲击的次数减少[11],进而使齿面弹塑性变形减小,强化层深度减小,齿面最大残余应力也会随之减小。
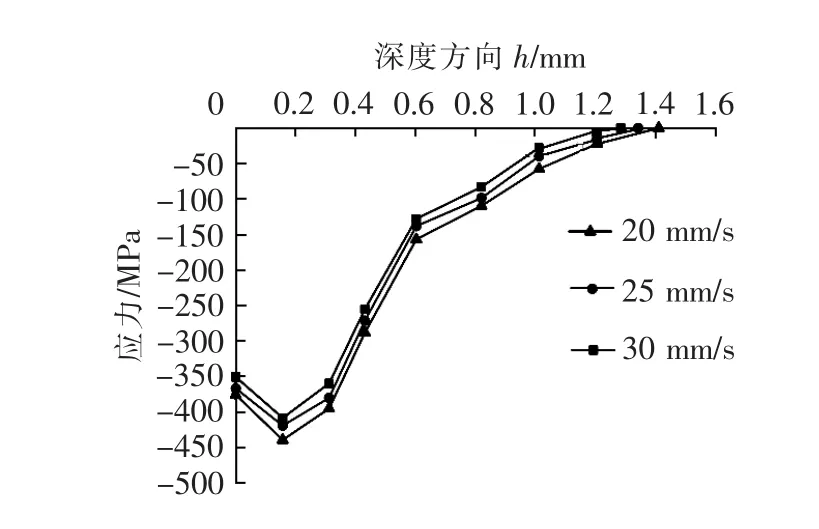
图6 不同进给速度下沿深度方向的应力分布图
2.4 振幅对齿面残余应力的影响
取静压力F=600 N、进给速度v=20 mm/s、频率f=20 kHz,研究不同振幅对残余应力的影响,结果见图7。可见,当振幅增加时,表面最大残余应力和应力层深度都会增大,但程度不是很明显。分析原因:在齿面超声挤压过程中,振幅影响动态冲击力[12],在其他工艺参数相同的情况下,不同振幅产生的动态冲击力差别较小,因此对残余应力影响也较小。

图7 不同振幅下沿深度方向的应力分布
3 结论
本文所建三维有限元模型可对齿轮齿面超声挤压强化后的残余应力进行准确模拟。经挤压强化后的齿轮表面产生残余压应力。当静压力增加时,残余应力会随之增大,残余应力深度也会随之有所增加;当工具头作用在齿面上的进给速度增加时,残余应力和残余应力深度会随之减小;当超声系统的振幅增加时,残余应力变化不是很明显。经有限元模拟可知,超声挤压强化技术不仅能用来强化规则的表面,对齿轮等不规则表面的强化同样会产生良好的提升效果。
参考文献:
[1]LIN Y C,CHEN Xiaomin,LIU Ge.A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel[J].Materials Science and Engineering A,2010,527(26):6980-6986.
[2]HOU Qingyu,WANG Jingtao.A modified Johnson-Cook constitutive model for Mg-Gd-Y alloy extended to a wide range oftemperatures [J].ComputationalMaterials Science,2010,50(1):147-152.
[3]UMBRELLOD,M′SAOUBIR,OUTEIRO JC.The influence of Johnson-Cook material constants on finite element simulation of machining of AISI 316L steel[J].International Journal of Machine Tools and Manufacture,2007,47(3-4):462-470.
[4]汤祁.面向45#钢切削残余应力仿真的JC本构模型参数和刀-屑摩擦系数的确定 [D].武汉:华中科技大学,2015.
[5]黄廷尊.超声冲击对材料力学性能的影响及冲击过程的有限元模拟[D].镇江:江苏科技大学,2016.
[6]LIU Yu,WANG Lijun,WANG Dongpo.Finite element modeling of ultrasonic surface rolling process[J].Journal ofMaterials Processing Technology,2011,211 (12):2106-2113.
[7]王琰.超声波滚压光整加工技术的实验研究 [D].沈阳:东北大学,2014.
[8]薛军,孙宝玉,辛宏伟,等.基于有限元法的齿轮齿条动态应力分析[J].长春工业大学学报,2008,29(3):275-278.
[9]杨磊.大模数齿轮齿条接触疲劳强度研究 [D].郑州:河南工业大学,2013.
[10]MOUSAVIS A A A,FEIZIH,MADOLIAT R.Investigations on the effects of ultrasonic vibrations in the extrusion process[J].Journal of Materials Processing Technology,2007,187-188(12):657-661.
[11]LIU Yu,WANG Lijun,WANG Dongpo.Study on ultrasonic surface rolling process using FEM analysis[J].Advanced MaterialsResearch,2011,189-193:2112-2115.
[12]候雅丽.纵扭复合振动超声深滚加工表面强化机理研究[D].焦作:河南理工大学,2015.
