超声纵振动空心变幅杆的特性

王维鸽，贺西平

（陕西师范大学 物理学与信息技术学院，陕西 西安710119）

超声振动系统主要由换能器和变幅杆等部件组成。变幅杆起着聚集超声能量、放大振幅和阻抗匹配等作用［1］。为了获得大振幅的变幅杆，文献［2］报道了外形为B样条曲线的变幅杆，该变幅杆的振幅放大系数比传统的悬链线变幅杆大41．1%，比贝塞尔曲线变幅杆大8．6%。Wang等［3］设计了贝塞尔曲线形变幅杆，仿真计算、测试表明贝塞尔曲线变幅杆的振幅放大倍数比传统的悬链形变幅杆大71%。文献［4］研究了5种形状的变幅杆，仿真计算的结果说明阶梯形和贝塞尔形变幅杆具有较大的放大系数。

对于传统形状变幅杆，在面积系数N相同时，阶梯形变幅杆的振幅放大系数最大，其次为悬链线形、指数形，最小是圆锥形。虽然如此，形状因数的顺序恰与此相反。

一般设计变幅杆的方法有解析法［5－6］、传输矩阵法［7］、等效电路法［8－10］、表观弹性法［11］和有限元法［12－13］等。随着超声加工技术应用日益广泛，为提高超声加工、处理的效率和质量，对振动系统的振幅等参数提出了更高要求。设计大放大系数的变幅杆，提高其能量转换效率显得极为重要［14］。

本文基于解析法和有限元法，研究了内孔分别为柱孔和锥孔的锥形变幅杆。利用解析法推导了这两种变幅杆的频率方程及各性能参数表达式；利用ANSYS有限元分析软件建立了这两种杆以及对应锥孔和柱孔填实的实心杆模型，计算了变幅杆的应力以及振动位移随轴向分布的规律。结果表明，当谐振频率和面积系数相同时，锥孔的锥形变幅杆放大系数最大，柱孔的次之，实心锥形变幅杆最小；不同形状变幅杆的位移节点与应变极大位置之和近似等于其半波长谐振长度。最后给出了各变幅杆的等效电路。

1 推导及计算

内孔为锥形和柱形、外形为锥形的变幅杆及对应空心部分填实后的实心锥形变幅杆如图1所示。

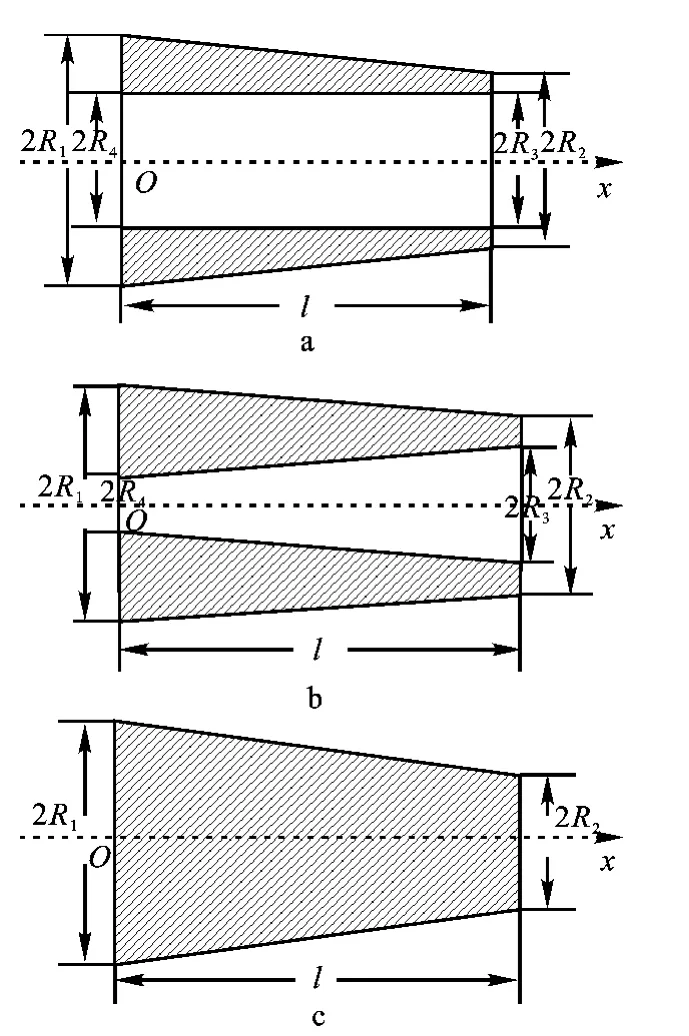
图1 内孔为柱形的锥形变幅杆（a），带有锥形孔的锥形变幅杆（b），实心锥形变幅杆（c）的示意图Fig．1 Sketch figurer of conical ultrasonic horn with a cylindrical central hole（a），Conical ultrasonic horn with a conical central hole（b）and the solid horn（c）

材料为45＃钢，其杨氏模量为2．09×1011N2／m，泊松比为0．28，密度为7 800kg／m3。不同形状变幅杆的编号及相应的几何尺寸如表1所示。为了便于比较，取各杆两端的外径相同。

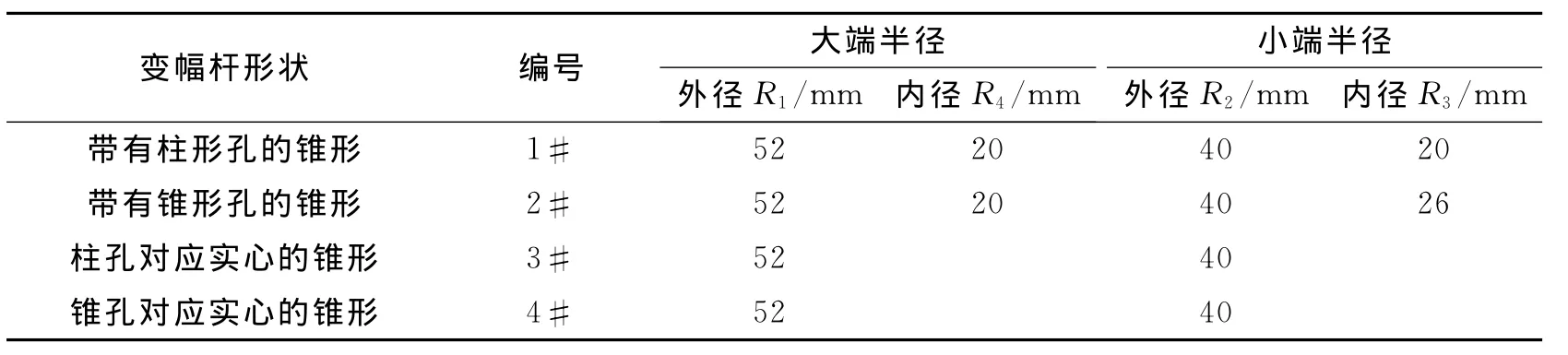
表1 变幅杆编号及几何参数Tab．1 The number and geometric parameters of the horns

1＃变幅杆的半径变化规律为α1＝（R1－R2＋R3－R4）／（（R1－R4）l），面积系数为N1＝（R1－R4）／（R2－R3）；2＃变幅杆的半径变化规律为α2＝（R1－R2）／（（R1－R4）l），面积系数为N2＝（R1－R4）／（R2－R3）；3＃与4＃变幅杆的半径变化规律为α3，4＝（R1－R2）／（R1l），面积系数为N3，4＝R1／R2。

1．1 频率方程及各性能参数表达式

变截面杆的一维纵向振动的波动方程其中k＝ω／c，k是波数；ω 是振动的圆频率；c＝是杆中一维纵振传播速度。已知中心带孔的锥形变幅杆截面变化规律为

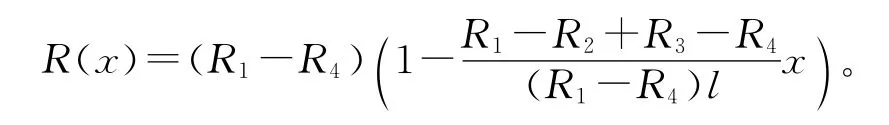
波动方程的解为

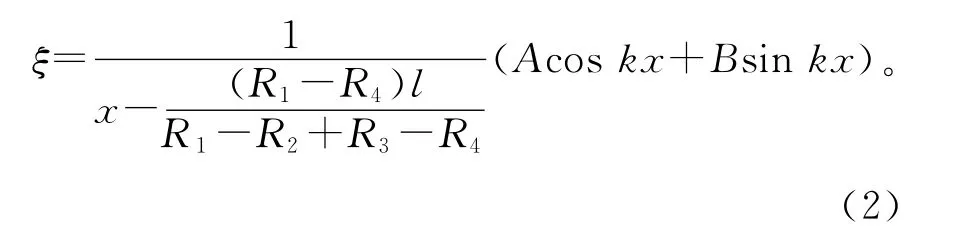
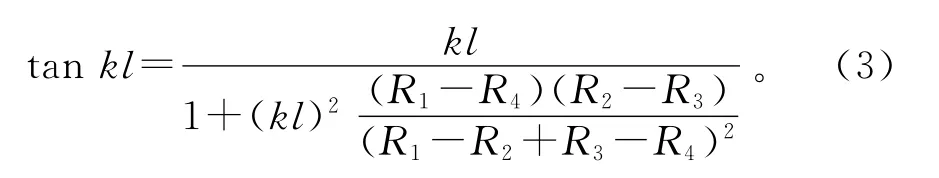
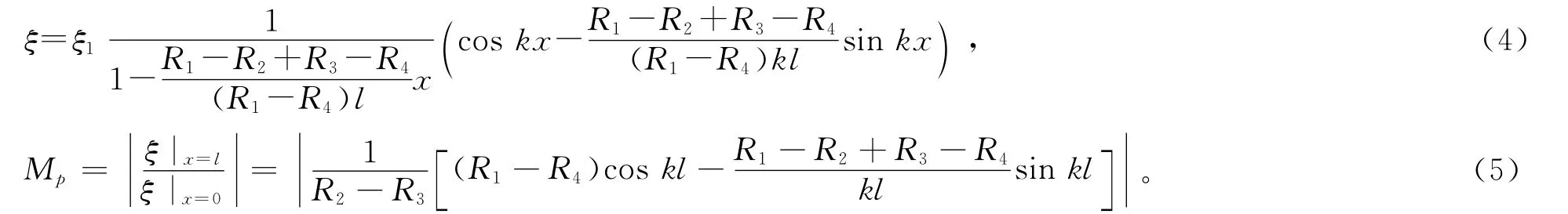
由式（4），当x＝x0时，ξ＝0，则位移节点x0为

1．2 性能参数的计算及分析

谐振频率为14～25kHz，将表1中的几何参数代入上面各表达式中，可计算得到谐振长度lp、位移节点x0、应变极大xM、放大系数Mp如表2所示。

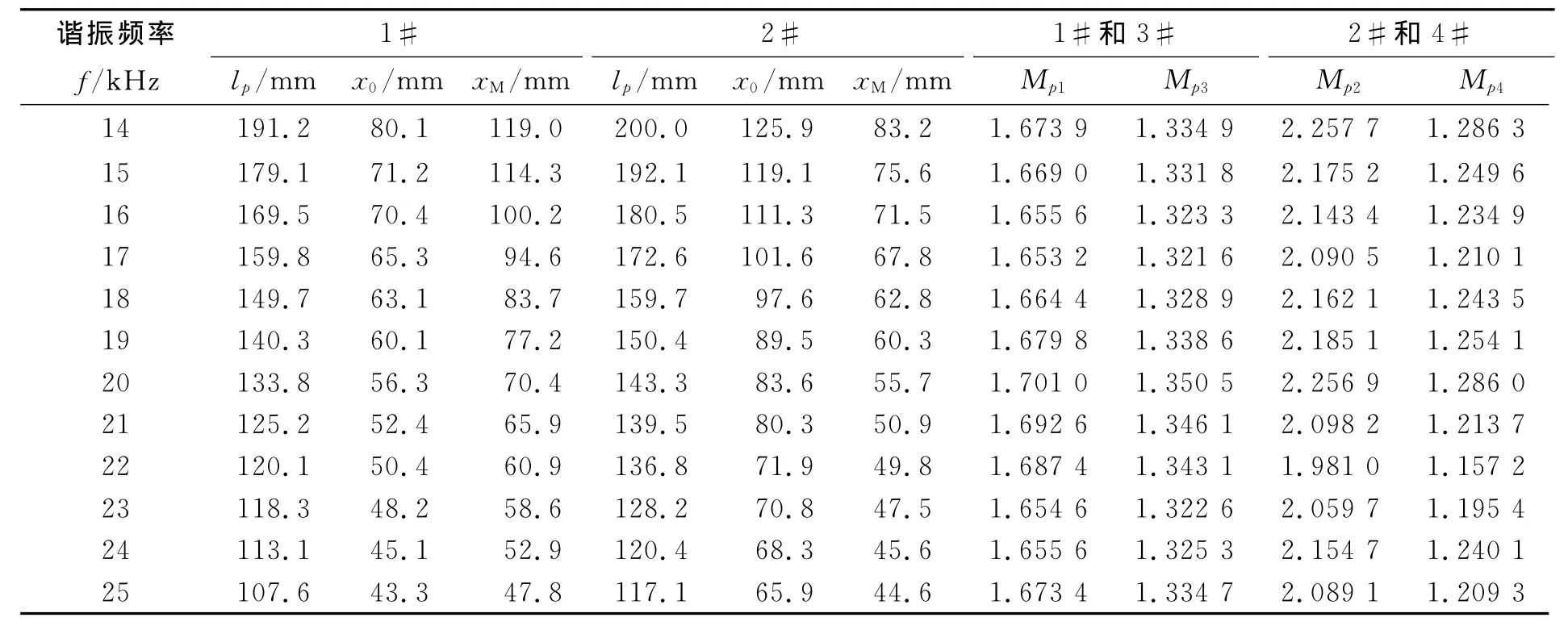
表2 变幅杆的各性能参数Fig．2 The kinds of performance parameters of the horns

各变幅杆的放大系数与谐振频率的关系，如图2所示。由图2可以看出，谐振频率与面积系数相同时，2＃变幅杆的放大系数最大，1＃变幅杆次之，3＃和4＃杆的放大系数相差不大，为最小。谐振频率为20kHz时，取实心悬链线、阶梯形变幅杆的大端和小端与表1中的几何尺寸相同，则1＃空心变幅杆的放大系数（小于2＃）比悬链线形的还大29．6%，与阶梯形的近似相等。

从图3和图4可以看出，在谐振状态下，1＃和2＃变幅杆的（x0＋xM）／lp都近似等于1，即1＃和2＃变幅杆应力极大的位置与位移节点之和与3＃变幅杆［15］的都近似等于对应变幅杆的谐振长度。

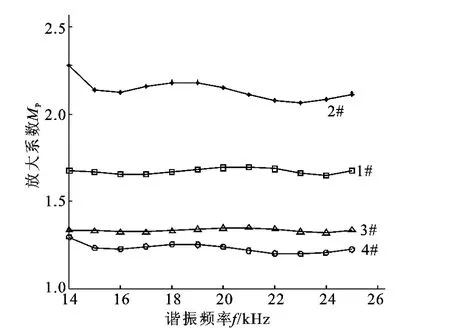
图2 不同形状变幅杆的放大系数与谐振频率的关系Fig．2 The relationship between amplification factor and resonant frequency with different horns

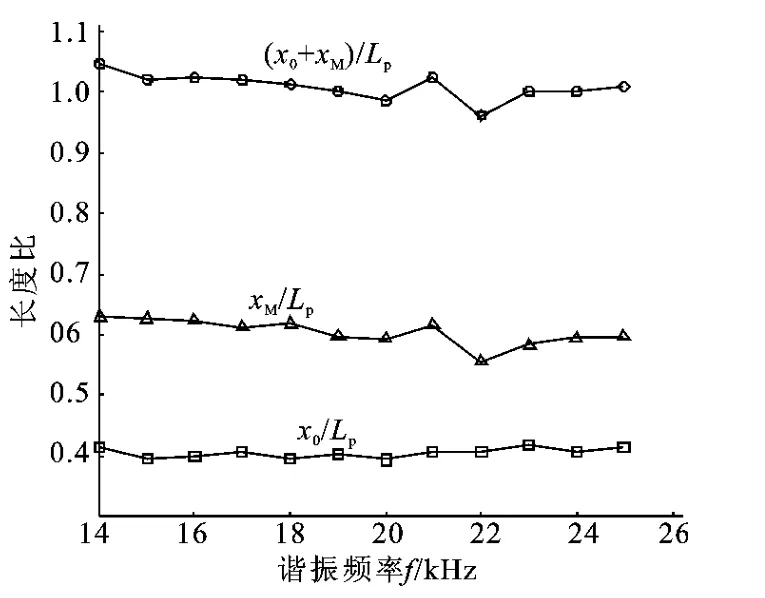
圆锥孔变幅杆各性能参数与谐振频率的关系The relationship between the parameters of the sonant frequency of horns with a conical central hole

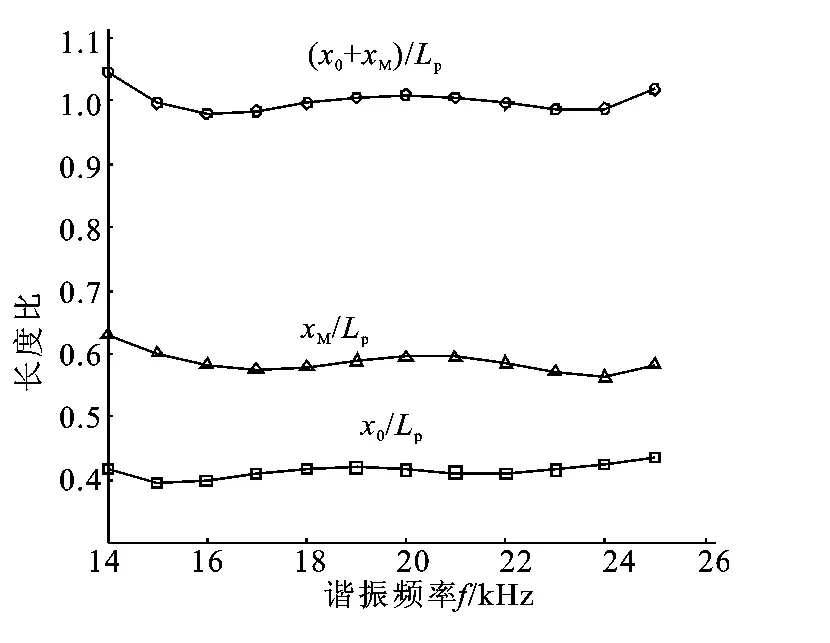
圆柱孔变幅杆各性能参数与谐振频率的关系．4 The relationship between the parameters and t frequencies of horns with a cylindrical central hole

2 有限元计算

建立有限元模型进行模态计算，得到不同形状变幅杆的谐振长度对应的一阶纵振频率（如表3所示）。在谐振状态下，各变幅杆的位移沿轴向分布如图5和6所示。

从图5和图6中可以看出，2＃变幅杆的放大倍数最大，1＃变幅杆次之，3＃和4＃变幅杆的放大系数相差不大，即为最小。沿轴向归一化应力分布和位移分布如图7和8所示。

表3 各变幅杆谐振长度对应的一阶纵振频率Fig．3 The first order frequencies of longitudinal vibration corresponding to their length of the horns

图5 圆柱孔与实心变幅杆沿轴向的位移分布Fig．5 Displacement distribution of the horns with a cylindrical central hole and solid horn

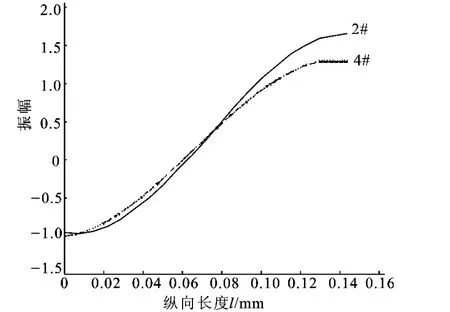
图6 圆锥孔与实心变幅杆沿轴向的位移分布Fig．6 Displacement distribution of the horns with a conical central hole and solid horn

图7 不同形状变幅杆沿轴向的应力分布曲线Fig．7 Stress distribution of kinds of the horns

图8 不同形状变幅杆沿轴向的位移分布曲线Fig．8 Displacement distribution of kinds of the horns

可以看出，在谐振状态下4种变幅杆应力极大的位置与位移节点之和近似等于对应变幅杆的谐振长度。1＃变幅杆的应变极大值xM＝0．071mm，位移节点x0＝0．06mm，xM＋x0＝0．131mm，近似为变幅杆的谐振长度。经理论推导，空心变幅杆的等效电路与实心变幅杆的等效电路相同［1］，只要将空心变幅杆对应阻的参数代入即可。

3 结论

本文基于解析法和有限元法，对4种不同形状的变幅杆进行了计算研究，得到如下结论：

（1）在相同面积系数和谐振频率下，空心变幅杆、阶梯形变幅杆的放大系数最大，依次为悬链线、指数形、圆锥形。

（2）在相同面积系数和谐振频率下，不同形状中心孔锥形变幅杆的放大系数顺序为：带有锥形孔的杆最大，柱形孔的次之，柱孔为实心的杆和锥孔为实心的放大系数相差不大，为最小。

（3）中空变幅杆的应力极大值大于对应空心部分填实的变幅杆。

（4）4种变幅杆的形状不同，等效电路却都相同，代入相应的几何参数就可以得到具体的机电等效电路。

（5）不同形状变幅杆的应变极大值点与位移节点之和近似等于对应变幅杆的半波长谐振长度。

［1］林仲茂．超声变幅杆的原理和设计［M］．北京：科学出版社，1984：53－126．

［2］Nguyen Hu T，Nguyen H D，Uan J Y，et al．A nonrational B－spline profiled horn with high displacement amplification for ultrasonic welding［J］．Ultrasonics，2014，54（3）：2063－2071．

［3］Wang D A，Chuang W Y，Hsu K，et al．Design of a B zier－profile horn for high displacement amplification［J］．Ultrasonics，2011，51：148－156．

［4］Roopa Rani M，Rudramoorthy R．Computational modeling and experimental studies of the dynamic performance of ultrasonic horn profiles used in plastic welding［J］．Ultrasonics，2013，53：763－772．

［5］贺西平，程存弟．几种常见形状函数超声变幅杆性能参量的统一表达［J］．陕西师范大学学报：自然科学版，1994，22（3）：29－32．

［6］贺西平，高洁．超声变幅杆设计方法研究［J］．声学技术，2006，25（1）：82－85．

［7］Lesniewski P．Discrete component equivalent circuit for Webster′s horns［J］．Applied Acoustics，1995，44：117－124．

［8］高洁，贺西平，胡静．四端网络法统一变幅杆的性能参量［J］．声学技术，2006，25（1）：87－89．

［9］顾煜炯，周兆英，姚健．超声振动系统的四端网络设计方法及其应用［J］．机械工程学报，1997，33（3）：95－100．

［10］赵福令，冯冬梅，郭东明，等．超声变幅杆的四端网络法设计［J］．声学学报，2002，27（6）：554－558．

［11］Mori E．New bolt clamped flexural mode ultrasonic high power transducer with one dimensional construction［C］∥Ultrasonics International Conference Proceedings，1989：256．

［12］Huang Yicheng，Ding Guanzhang，Chen Bohsuan，et al．Simulation and experiment of langevin－type piezoelectric ultrasonic horn for micro tool motion［J］．Intelligent Technologies and Engineering Systems，2013：967－974．

［13］Xiao Guorong，Xu Xuemiao．Study on bezier curve variable step－length algorithm［J］．Physics Procedia，2010，25：1781－1786．

［14］潘巧生，刘永斌，贺良国，等．一种大振幅超声变幅杆设计［J］．振动与冲击，2014，33（9）：1－5．

［15］刘豆豆，贺西平，李家星．变幅杆位移节点和应变极大位置的关系［J］．陕西师范大学学报：自然科学版，2014，42（3）：49－51．