导数法求解三角函数asinωx+bcosωx的周期初探
2018-05-09罗元皓
罗元皓
(北京交通大学附属中学高三(8)班 100081)

众所周知,对于任意一个存在一阶和二阶导数的函数(三角函数总是存在的),其一阶导数的零点就是函数的极值点,再结合二阶导数就可判断出极大值与极小值.二阶导数大于0的点为极小值,否则为极大值.而且,对于周期的三角函数,这些极大(小)值点连接起来就是一条平行于横轴的直线,而且一定存在许多这样的极值点.因此,相邻两个极大(小)值点之间的距离对应的就是该三角函数的周期.其实,对于周期函数,这些极大值与极小值一定是交替出现且等间隔的,所以,其周期就是任意两个相邻极值点间距离的2倍(此时,就无须再区分极大值与极小值).
确定了极大值与极小值的取值点,单调区间也就确定了.一阶导数大于0即单调递增区间,也就是区间 [极小值点,右边相邻极大值点];一阶导数小于0即单调递减区间,也就是区间 [极大值点,右边相邻极小值点].
实例求下列三角函数的周期:
(1)sin2x;
(2)sin2x+cos2x;
(3)3sin2x+5cos2x.
解法1(直接法) 利用sinωx和cosωx的周期均为2π/ω,先确定三角函数的ω,或者将三角函数的代数运算合并为一个角的一种三角函数后再直接使用公式2π/ω求解即可.
(1)sin2x的ω=2,周期T=π.
(2)sin2x和cos2x的周期均为π,故sin2x+cos2x的周期也是π.
或者,利用三角函数和差与积的关系进行变换
sin2x+cos2x

(3)3sin2x和5cos2x的周期均为π,故3sin2x+5cos2x的周期也是π.
3sin2x+5cos2x

解法2(导数法) 对于任意一个函数,其一阶导数的零点是极值点.而对于周期函数,这些极大(小)值点连接起来就是一条平行于横轴的直线,而且一定存在许多这样的极值点.因此,相邻两个极大(小)值点之间的距离对应的就是该函数的周期.极大值与极小值可利用二阶导数的极性来进行判断,二阶导数大于0为极小值,否则为极大值.其实,对于周期函数,这些极大值与极小值一定是交替出现的,所以,其周期就是任意两个相邻极值点间距离的2倍.
(1)sin2x的一阶导数是2cos2x,二阶导数是-4sin2x.


单调递减区间
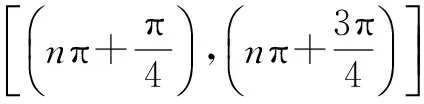
单调递增区间

(2)y=sin2x+cos2x的一阶导数是y′=-2sin2x+2cos2x,二阶导数是y″=-4sin2x-4cos2x.
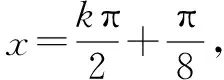

单调递减区间

单调递增区间

(3)y=3sin2x+5cos2x的一阶导数是y′=-6sin2x+10cos2x,二阶导数是y″=-12sin2x-20cos2x.
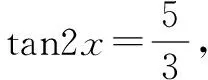

单调递减区间

单调递增区间
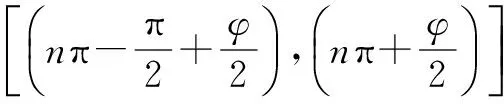
小结导数法将问题转化为求解方程问题,且同时很容易就能得到三角函数的极值和单调区间,更加方便可行.
参考文献:
[1]苏飞文,洪丽敏。探究导数思想在三角函数性质中应用[J].福建中学数学,2013.
