亚波长间距理想导体球阵列近区时间反演电磁场的快速求解∗

2018-05-08龚志双王秉中王任

物理学报 2018年8期

龚志双王秉中王任

(电子科技大学应用物理研究所,成都 610054)

(2017年11月22日收到;2017年12月27日收到修改稿)

1 引言

时间反演技术能够简单地重构出辐射源的位置信息.在自由空间中,点源的反演场幅度在空间呈类似sinc函数的分布,其第一个过零点即对应半波长的位置,也就意味着极限聚焦分辨率为半波长[1−3].分辨率受限的本质原因是近场凋落波无法传播至远场,因此要从本质上突破半波长的极限,必须在近场区域对凋落波进行操作[4−7].在近场区域有散射体存在的情况下,时间反演技术能够实现超分辨率(小于半波长)的聚焦[8−11].但是,前述研究主要通过仿真软件进行反演场的计算,求解过程费时而且没有严格的理论指导.因此,研究有散射体加载情况下反演场的解析解,就显得尤为重要.金属小球作为结构最简单的散射体,也可以认为是复杂散射体的基本组成部分,是本文的主要研究对象.时间反演场的严格解析解可以通过时间反演腔理论进行求解,但前提是已知正向场对应的格林函数[12].

关于金属球的散射格林函数早已有严格的解析解[13−17],但是,前述论文中给出的结果均是将不同区域的场分别展开为球矢量波函数叠加的形式,之后再利用边界面上的场应该满足的边界条件对展开系数分别求解.如此求解出来的结果为无穷级数求和的形式,当空间中包含多个散射体时,上述方法的求解会非常复杂[18,19].用基于等效偶极子分析的思路可以较快速地求解复杂物体的散射格林函数[20,21],尤其在处理多散射体问题时优势比较明显.

本文在已有研究的基础上,提出了球面波入射情况下基于等效偶极子分析的反演场快速求解方法.通过将金属小球的散射场等效为电磁偶极子辐射场的叠加,极大地简化格林函数的求解.在包含有多个散射体时,只需要将每一个金属球的散射场均等效为相应的电、磁偶极子辐射场的叠加,在求解出等效偶极子强度之后,空间中总场对应的格林函数即可表示为所有等效电磁偶极子的贡献之和.

本文第2部分详细给出球面波入射情况下金属小球的散射场求解及其相应的等效方法;第3部分给出总场对应并矢格林函数的表达式;第4部分给出几种不同情况下相应时间反演场的解析求解结果以及商业软件仿真结果,以验证所提出的等效方法的正确性;最后,利用所提出的分析方法对加载散射体情况下源的聚焦分辨率做了初步研究.结果表明,利用所提等效模型可以对多金属小球加载情况下的时间反演场进行快速求解,为实现时间反演超分辨特性的加载散射体结构设计提供理论指导.

2 偶极子源激励情况散射场求解

2.1 水平电偶极子源激励情况

求解模型示意图见图1.散射体为一位于坐标原点处、半径为a的金属球,激励源为一处于r′=(0,0,b)位置处的水平电偶极子,并有b>a(即源在散射体外),相应的电偶极子矢量为pe=Ielex,其中Ie为电流强度,l为元的长度.场观测点的球坐标位置为(r,θ,ϕ).真空中介质的介电常数和磁导率分别为ε和µ.下面表达式中上标为“inc”的表示入射场,上标为“sca”的表示散射场,下标为“equ”的代表等效结果.k代表自由空间中传播波数;ω为角频率;η0为自由空间波阻抗;r为场观测点到原点的距离;R为场观测点到初始激励源的距离.为第一类连带勒让德函数;分别为三种不同类型的球贝塞尔函数.

为了对凋落波进行操作使其能转化为传输波,需要所加载的散射体尺寸与相应的空间频率相对应,而凋落波对应较高的空间频率分量,因此要求所加载的散射体尺寸相对自由空间波长较小.所以本文主要考虑加载散射体尺寸远小于自由空间波长的情况(即ka<1).同时,因为凋落波随传输距离呈指数衰减,需要在其衰落至太小之前对其进行操作,也即意味着需要在源的近场区进行加载.故本文只讨论源与散射体之间间距小于半波长(即kb<π)的情形.

根据文献[11]中的结果可以得到图1所示场景散射场的表达式为

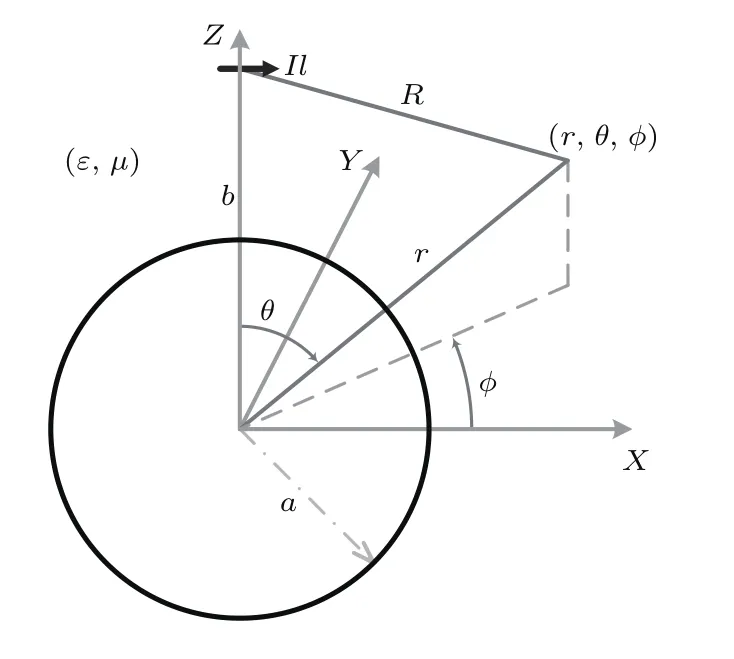
图1 水平电偶极子激励情况示意图Fig.1.Diagram with an excitation source of electric dipole.

其中cen和den分别为

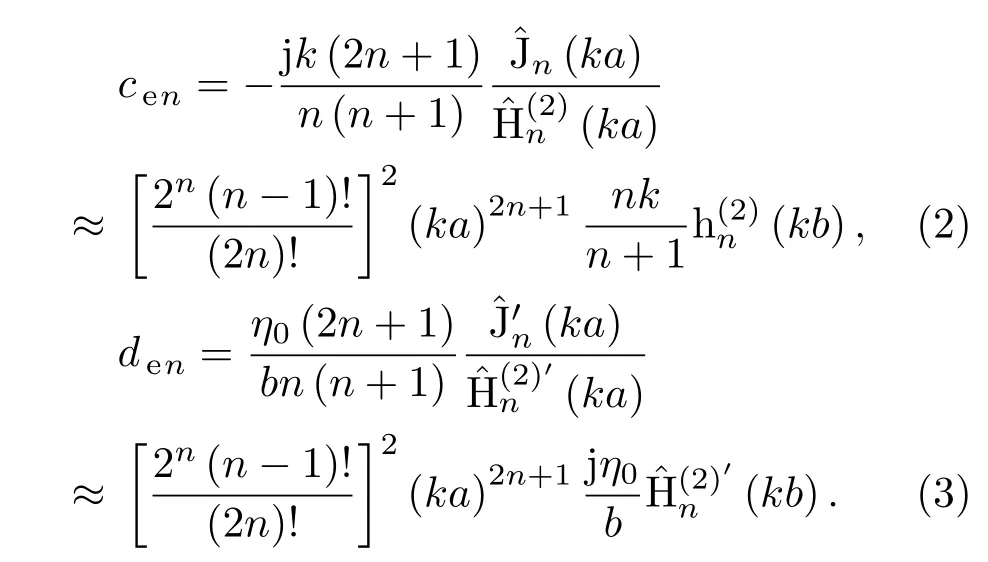
设场观测面为z=b平面,将(2),(3)式代入(1)式,计算观测面上其前两项绝对值的最大值之比ρ随a和b的变化情况,如图2(a)所示.由图2(a)可知,ρ=10的等高线近似为一条直线,对其进行线性拟合的结果为b=1.2646a+0.1168λ.另外,由贝塞尔函数的特性可知,更高次项的绝对值会越来越小.以ρ值大于10为依据可知,当b>1.2646a+0.1168λ且a<0.08λ时可以近似采用(1)式的第一项代表整体散射场.当a=0.03λ,b=0.3λ时,(1)式前三项绝对值大小沿观测面上x轴的分布如图2(b)所示,可以看到此时第二、三项的值确实远小于第一项.

图2 水平电流源激励情况下散射电场级数展开式 (a)前两项绝对值最大值之比随a和b的变化情况;(b)前三项绝对值沿x轴分布情况(其中a=0.03λ,b=0.3λ,观测面为z=b平面.以下所有类似场幅度值分布图所对应的计算场景与此图相同)Fig.2.Series expansion of the scattered electric field with horizontal excitation electric dipole:(a)Relationship of the ratio between the maximum absolute value of the first two terms with a and b;(b)absolute value distribution of the first three terms along x-axis in the plane z=b(with a=0.03λ,b=0.3λ.The calculation scenery bellow is the same as this figure).

将(2)式和(3)式代入(1)式得到第一项的表达式为

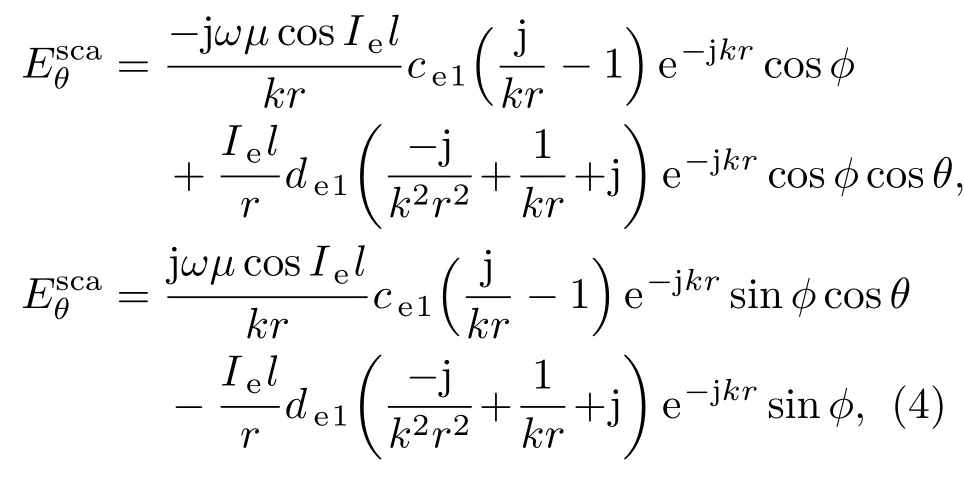
对比沿x方向电偶极子及沿y方向磁偶极子的辐射场[20]可以发现,此散射场等于一电偶极子和一磁偶极子辐射场的叠加.相应的电磁偶极子矢量分别为

2.2 垂直电偶极子源激励情况

对于图1所示的模型,当激励源的极化方向为沿z轴时,电偶极子强度可表示为pe=Ielez.根据对称性并且考虑小金属球情况可得散射场表达式为

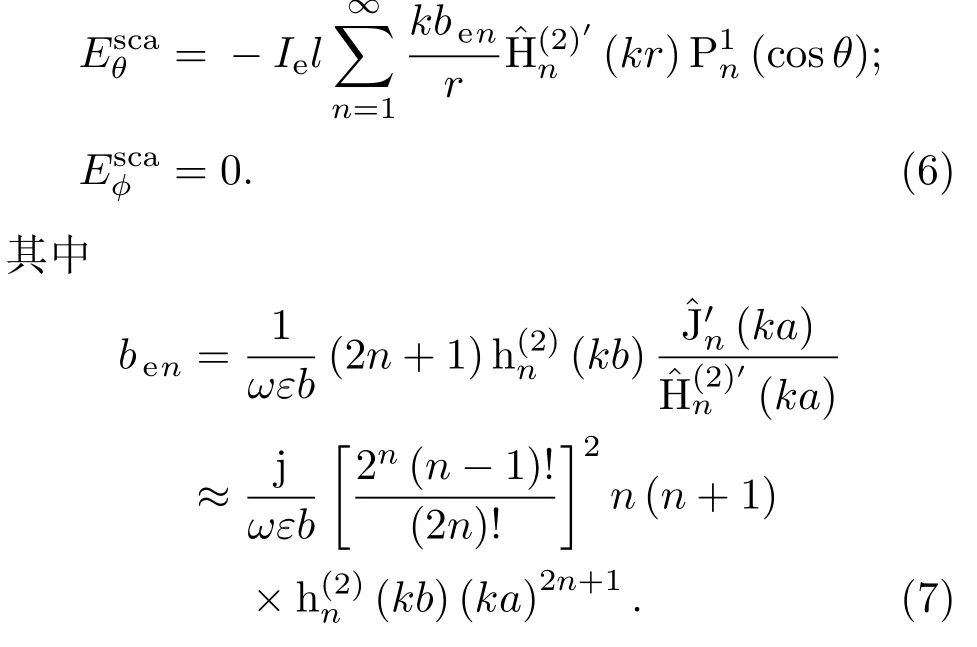
(6)式前三项绝对值分布的计算结果如图3所示.仍以ρ>10为判断标准,当b>1.0429a+0.1416λ

图3 垂直电流源激励情况下散射电场级数展开式 (a)前两项绝对值最大值之比随a和b的变化情况;(b)前三项绝对值沿x轴分布情况Fig.3.Series expansion of scattered electric field with vertical excitation electric dipole:(a)Relationship of the ratio of the maximum absolute value of the first two terms with a and b;(b)absolute value distribution of the first three terms along x-axis in the plane z=b.

且a<0.08λ时,可以只取(6)式的第一项代表整体散射场,其表达式为

对比沿z方向极化电偶极子的辐射场可知,此时散射场等于一电偶极子的辐射场.相应的等效电偶极子矢量为

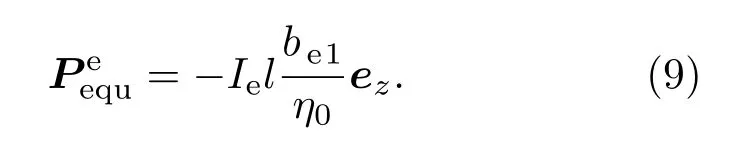
2.3 水平磁偶极子源激励情况

当激励源为磁偶极子并且极化方向为沿x轴时,磁偶极子矢量可表示为pm=Imlex,其中Im为磁流强度.利用前面计算得到的电偶极子激励情况的结果并根据电与磁的对偶性可得此时散射场的表达式为:

(10)式前三项绝对值分布计算结果如图4所示.类似可得当b>0.9938a+0.1248λ且a<0.08λ时,其第一项的值远大于高阶项的值.取(10)式的第一项可得散射电场的表达式为:

对比沿x方向极化磁偶极子及沿y方向极化电偶极子的辐射场可以发现,此时散射场等于一磁偶极子与一电偶极子辐射场之和,相应的偶极子矢量分别为:

图4 水平磁流源激励情况下散射电场级数展开式 (a)前两项绝对值最大值之比随a和b的变化情况;(b)前三项绝对值沿x轴分布情况Fig.4.Series expansion of scattered electric fi eld with horizontal excitation magnetic dipole:(a)Relationship of ratio between maximum absolute value of the fi rst two terms with a and b;(b)absolute value distribution of the fi rst three terms along x-axis in the plane z=b.

2.4 垂直磁偶极子源激励情况

当激励源为一沿z向极化的磁偶极子时,磁偶极子强度矢量为pm=Imlez.利用对称性可以由磁Hertz矢量位求解得到散射电场的表达式为:

其中

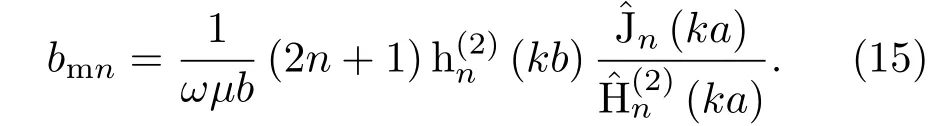
相应的(14)式前三项的绝对值分布如图5所示.

当b>4.1361a−0.0251λ且a<0.08λ时,其第一项的值远大于高阶项的值.取第一项代替整体散射场可得

对比沿z方向极化的磁偶极子的辐射场可以发现此时散射场就等于一磁偶极子的辐射场,相应的磁偶极子矢量为

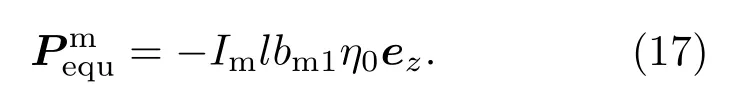
图5 垂直磁流源激励情况下散射电场级数展开式 (a)前两项绝对值最大值之比随a和b的变化情况;(b)前三项绝对值沿x轴分布情况Fig.5.Series expansion of scattered electric fi eld with vertical excitation magnetic dipole:(a)Relationship of the ratio between maximum absolute value of the fi rst two terms with a and b;(b)absolute value distribution of the if rst three terms along x-axis in the plane z=b.

取上面4种情形满足ρ值大于10的公共区间可得,当b>2.2875a−0.1043λ且a<0.08λ时,无论初始激励源极化如何,均可采用散射场级数展开式的第一项代替整体散射场,即意味着可以将散射电场等效为电磁偶极子辐射场之和.

3 多金属球散射体情况并矢格林函数分析

当有多个金属小球散射体时,对每个金属球而言,在求解总等效偶极子矢量时应考虑其余所有金属球等效偶极子与初始激励源的贡献之和.将第j个散射体的等效电、磁偶极子矢量分别记为Pej和Pmj,其中j∈[0,1,···,N],N为散射金属球的个数.初始激励源视为0号散射体,其对应的电磁偶极子矢量大小即等于初始源的实际分量.分别将Pei和Pmi分解为相应的水平和垂直分量,即可得到每一个金属小球的等效偶极子为

其中I为单位矩阵.因此可以得到此情况下的电并矢格林函数为

4 时间反演场数值求解结果

根据文献[12]指出的电流源远场时间反演场对应的格林函数与正向场对应格林函数的关系可知,初始电流源对应的时间反演格林函数为

其中imag[·]代表取虚部操作. 将(21)式代入(22)式即可得到时间反演格林函数的表达式.并由文献[12]的结论可得相应的时间反演场表达式为

4.1 单散射体情况

首先考虑简单情况,金属球位于坐标原点,激励源位于z轴上.假设金属球半径为a=0.03λ,所在的位置为(0,0,0),初始激励电流源所在的位置为(0,0,h),其中h=0.1λ.相应的位置分布示意图见图6.如无特别说明,以下所有算例中初始激励源的极化方向和所处位置均与此例一致.

图6 初始源及散射体分布位置示意图Fig.6.Distribution diagram of the excitation dipole and the scatterer.

根据(21)式和(22)式可得到此时的时间反演电并矢格林函数为

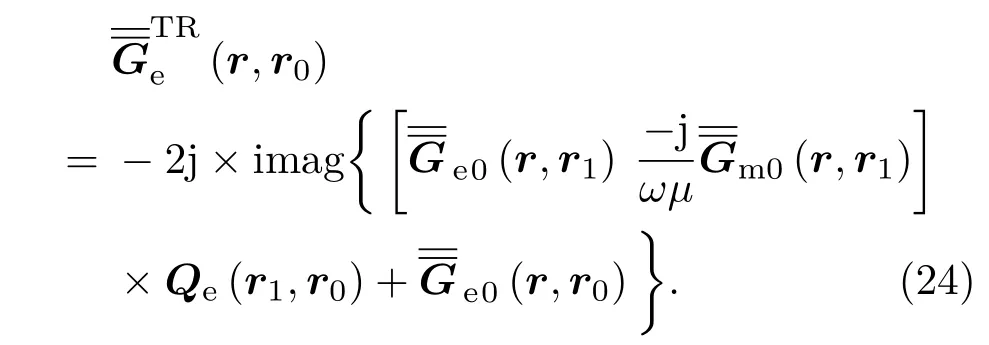
根据CST仿真和由(24)式计算得到的反演电场分布分别如图7所示(以下所有场观测面均默认为z=0.1λ平面).因为入射场的Ex和Ey分量远大于散射场的相应分量,引入散射体并不会明显改变其分布,因此以下只给出反演电场Ez分量的对比情况.

通过计算场值大小对应数值矩阵的相关性即可得到场解的相似度.矩阵的相关性Corr可以通过以下公式计算得到[22]:

其中xij和yij分别代表两个矩阵中的不同元素;和为相应的平均值.

计算反演腔内反演电场的相似程度即可得知解析结果是否正确.因为反演场主要集中在±0.5λ的范围之内,因此下面求解二者相似度时只考虑此范围内的场.利用(25)式计算得到图7(a)和图7(b)中黑色框内反演电场的相似度为0.9817,可以发现二者几乎完全一样,这也说明了解析计算结果的正确性.同时图7(c)给出了由CST和解析方法求解得到的反演场沿y=0直线的分布对比情况,可以看到,二者符合度非常高.

4.2 多散射体情况

利用所提方法计算反演场的最大优势在于求解速度快,尤其是在散射体数量较多的时候,不需要进行复杂的边值问题求解.待求解场景源与散射体的分布如图8所示.金属球所处的位置分别为r1=(d,0,0),r2=(0,0,0),r3=(−d,d,0),r4=(−d,−d,0),其中d=0.3λ.

图7 反演电场Ez分布图 (a)CST计算结果;(b)MATLAB解析计算结果;(c)两者结果沿y=0直线分布对比Fig.7. Distribution of time reversal field Ez:(a)CST result;(b)theoretical result of MATLAB;(c)comparison of field distribution along y=0 line.

图8 初始源及散射体分布位置示意图Fig.8.Distribution diagram of the excitation dipole and the scatterers.

图9 反演电场Ez分布 (a)CST计算结果;(b)MATLAB解析计算结果;(c)二者结果沿y=0直线分布对比Fig.9.Distribution of time reversal field Ez:(a)CST result;(b)theoretical result of MATLAB;(c)comparison of field distribution along y=0 line.

与单散射体情况类似,由CST计算得到的结果如图9(a)所示,相应采用(21)—(23)式可以得到反演场分布如图9(b)所示.同样,根据(25)式可以计算得到此时解析解与仿真解的相似度为0.9348,二者相似度依旧非常高.同时图9(c)给出的CST计算结果和解析结果沿y=0直线的分布对比图也很好地表明了二者的相似程度.

加载金属小球的最终目的是为了辅助实现源目标的超分辨率聚焦.综合以上计算结果可以发现,解析方法计算结果与商业软件CST仿真结果基本一致,这充分说明了解析推导的正确性.

图10 初始源及散射体分布位置示意图Fig.10.Distribution diagram of the excitation dipole and the scatterers.

图11 反演电场Ez分布图 (a)空间分布情况(MATLAB结果);(b)反演场幅值沿图(a)虚线分布情况Fig.11.Distribution of time reversal field Ez:(a)Spatial distribution(MATLAB result);(b)field distribution along dotted line in Fig.(a).

下面通过一个具体算例来考察加载金属小球之后源目标的聚焦分辨率情况.仿真模型的设置如图10所示,三个小金属球所处的位置分别为r1=(0,d,0),r2=(0,0,0),r3=(0,−d,0),其中d=0.3λ.相应反演场的求解结果如图11所示.考虑到磁流源反演场与电流源反演场的差异性,其空间分布并不是呈现中间大周围小的“sinc函数式”分布,而是呈现类似图7所示的“8字形”分布,因此不能通过直接观察整个空间场幅度大小分布来确定聚焦分辨率的大小.将一个“8字形”的分布看作一个整体,考察不同“8字形”整体最大场幅值的分布情况,即考察反演场幅度沿图11(a)所示虚线的分布情况.相应结果如图11(b)所示.可以看到,相距0.3λ位置处的反演场幅度值比最大幅值的1/2还小.以场幅值减小1/2作为可分辨的临界标准,可得出结论,反演场的聚焦分辨率是小于λ/2的.

5 结论

基于等效偶极子模型,提出了一种快速求解亚波长间距金属小球阵列加载情况下时间反演场的快速求解方法.分析结果表明,在金属球半径及其与激励源之间间距满足一定关系时,近场区域的散射场能够等效为电磁偶极子辐射场的叠加.在求解多散射体情况的散射场时,只要金属小球之间间距与小球半径大小之间也满足前述关系,就可以采用该近似将所有金属小球等效为相应的电磁偶极子.在利用该方法得到的并矢格林函数的基础上,根据时间反演腔理论能够快速地得到相应时间反演场的解析解.文章通过与由商业软件CST求解得到的时间反演场分布结果进行的对比表明,两种方法的求解结果数据符合度高达90%以上,这很好地验证了本文所提出模型的正确性.同时结合所提出方法进行的计算结果表明,通过在源的近场加载金属小球能够实现0.3λ的源目标聚焦分辨率.该等效模型的建立为后续快速分析小金属球散射体加载情况下的时间反演场分布提供了一种高效便捷的处理思路及理论指导.同时对后续高效研究如何进行合适的散射体加载以实现更高的聚焦分辨率提供了很好的分析工具.

[1]Parvulescu A,Clay C S 1965Radio Electron.Eng.29 223

[2]Fink M 1992IEEE Trans.Ultrason.Ferroelectr.Freq.Control39 555

[3]de Rosny J,Fink M 2007Phys.Rev.A76 065801

[4]Fang N,Liu Z,Yen T J,Zhang X 2003Opt.Express11 682

[5]Liu Z,Fang N,Yen T J,Zhang X 2003Appl.Phys.Lett.83 5184

[6]Grbic A,Eleftheriades G V 2004Phys.Rev.Lett.92 117403

[7]Pendry J B 2000Phys.Rev.Lett.85 3966

[8]Malyuskin O,Fusco V 2010IEEE Trans.Antenna.Propag.58 459

[9]Lemoult F,Lerosey G,de Rosny J,Fink M 2010Phys.Rev.Lett.104 203901

[10]Ourir A,Fink M 2014Phys.Rev.B89 115403

[11]Jouvaud C,Ourir A,de Rosny J 2014Appl.Phys.Lett.104 243507

[12]Carminati R,Pierrat R,de Rosny J,Fink M 2007Opt.Lett.32 3107