可压流体Rayleigh-Taylor不稳定性的离散Boltzmann模拟∗

李德梅赖惠林许爱国张广财林传栋4)甘延标5)

1)(福建师范大学数学与信息学院,福建省分析数学及应用重点实验室,福州 350117)

2)(北京应用物理与计算数学研究所,计算物理国家重点实验室,北京 100088)

3)(北京大学,应用物理与技术研究中心,高能量密度物理数值模拟教育部重点实验室,北京 100871)

4)(清华大学能源与动力工程系,燃烧能源中心,北京 100084)

5)(北华航天工业学院,廊坊 065000)

(2017年9月4日收到;2018年1月29日收到修改稿)

1 引 言

当低密度流体支撑或推动较高密度流体时,即重力加速度或惯性加速度由重密度流体指向轻密度流体时,如果流体之间的界面存在扰动,那么界面的扰动幅度将会增长,该物理现象称为瑞利泰勒(Rayleigh-Taylor,RT)不稳定性.这种不稳定性最早由Rayleigh[1]和Lamb[2]在某种程度上提及,直到1950年,Taylor明确指出不稳定性现象[3].因此,该现象也称为RT不稳定性或者Rayleigh-Lamb-Taylor不稳定性.由于RT不稳定性现象在惯性约束聚变[4−6]、超新星爆炸[7]、核反应堆[8]等领域中起着重要的作用,因此在过去几十年里,人们采用各种解析方法和数值方法对其进行研究,包括分子动力学[9]、直接数值模拟[10]、大涡模拟方法[11]等.这些研究对理解RT不稳定性现象的动力学机制提供了许多有用的信息.

作为Boltzmann方程的特殊离散形式,格子Boltzmann方法(lattice Boltzmann method,LBM)在各种复杂流体的研究中取得了巨大的成功[12].LBM在RT不稳定性问题的研究中发展了两类模型:不可压LBM[13−15]和可压LBM[16].这些模型的基本思想上是把LBM看作Navier-Stokes(NS)方程的求解器,能够模拟得到NS方程一致的结果.近年来,许爱国课题组[17−25]已将LBM发展成为能够同时描述流动和热动非平衡效应的离散Boltzmann方法 (discrete Boltzmann method,DBM).在2012年，许爱国等[17]提出构建DBM.DBM与LBM最主要的差异在于:作为偏微分方程解法器的LBM必须忠诚于原始物理模型,而作为流体系统动理学模型的DBM必须具有超越原始物理模型的部分功能;LBM所依赖的演化方程和“矩关系”可以根据算法设计的要求人为构造,即可以没有物理对应,而DBM所依赖的演化方程和“矩关系”只能是Boltzmann方程及其动理学矩关系,必须与非平衡统计物理学基本理论自洽[18].例如DBM所提供的非平衡行为特征能够恢复真实分布函数的主要特征[26]、区分不同类型的界面[27]、区分相分离过程的不同阶段[18,21],所提供的冲击波精细物理结果与分子动力学数值模拟结果相互印证,相互补充[28].本文在甘延标等[29]提出的DBM模型的基础上,进一步验证了含外力项的DBM模型.通过数值模拟Riemann问题和热Couette流等问题验证了DBM的有效性.使用该模型,本文模拟了可压流体系统多模初始扰动的RT不稳定性现象,能够得到RT不稳定性的基本物理图像以及相伴随的热动非平衡效应规律,得出一些相关物理解释.

2 离散Boltzmann模型

考虑含外力项的Bhatnagar-Gross-Krook(BGK)碰撞的Boltzmann方程为

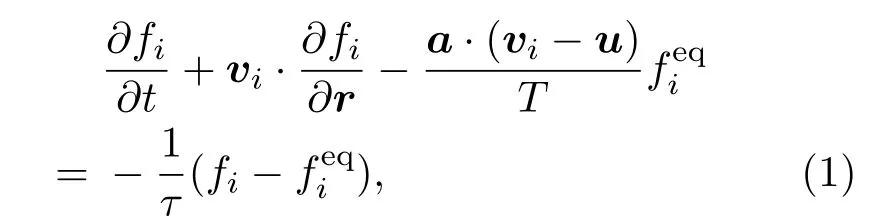
其中fi(r,vi,t)是离散分布函数,r是空间变量,t是时间;vi是离散速度,i=1,2,···,N是离散速度序号;u是宏观流速;a是加速度;τ是动理学松弛时间;是 Maxwell分布函数的离散化形式;其中Maxwell分布函数的形式如下:

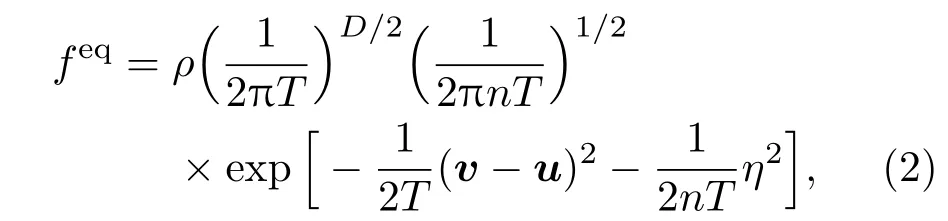
其中,D为空间维数(本文考虑D=2的情形);n是除了平动自由度之外的额外自由度数目;η是自由参数;ρ,T和u分别是密度、温度和流速.这里考虑的包含外力的方程是不包含外力情形下的拓展,可以处理更加普遍的物理情形,比如重力场存在下的流体不稳定性问题、分子间相互作用下的多相流问题、电场力、磁场力存在下的等离子体输运问题;其中的外力项使用了f∼feq的近似条件,因而该DBM只适用于系统偏离平衡不远的情形.

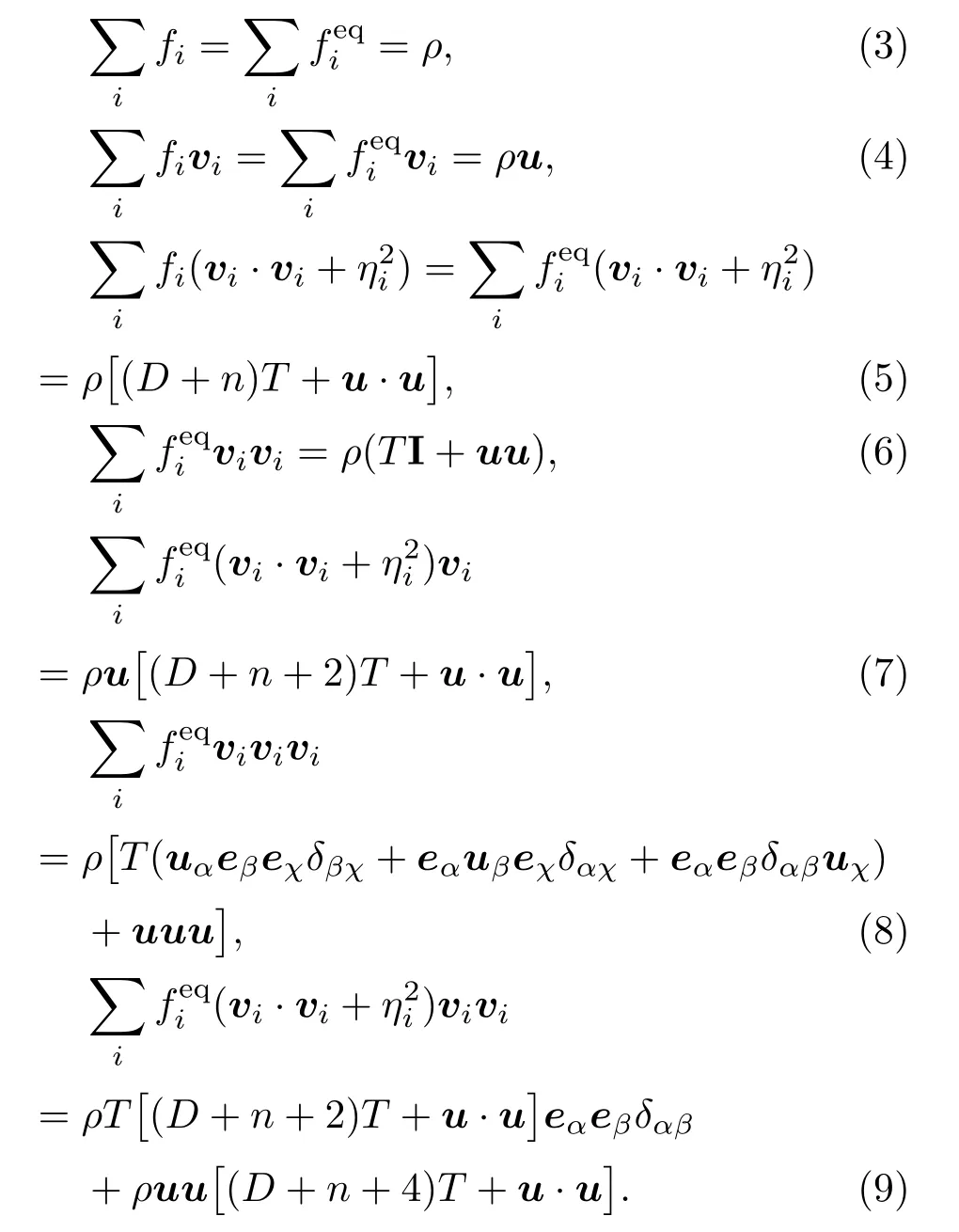
前三个方程代表质量守恒、能量守恒和动量守恒.

借助 Chapman-Enskog多尺度分析,可以从离散Boltzmann方程(1)得到NS方程层次的宏观流体力学方程.首先对密度分布函数、时间导数、空间导数和外力项进行如下多尺度展开:

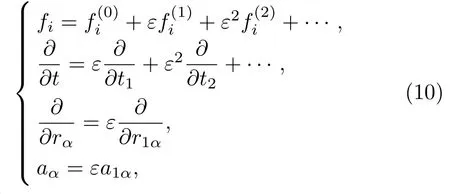
其中ε≪1是一个无量纲小量,正比于克努森数(Knudsen number,Kn)Kn=l/L,l是分子平均自由程或者平均分子间距,L是宏观上关心的特征尺度.

将方程(10)代入方程(1)中,可以得到一系列关于ε的各阶等式:

即分布函数的非平衡部分对宏观物理量没有贡献.

经过一系列代数运算,可以得到可压NS方程:

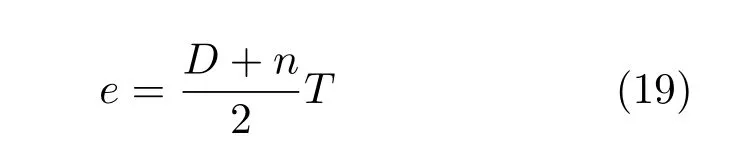
分别是压强和总内能;

为动力黏性系数;

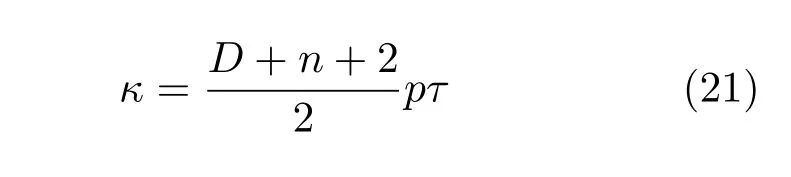
为热传导系数.

本文选取如下二维十六速度(D2V16)的离散速度模型: 其中,当i=1,2,···,4 时,ηi=η0,当i=5,6,···,16 时,ηi=0.

DBM摆脱了空间离散化和时间离散化之间的绑定,使得粒子速度可以灵活选择,并且可以在离散Boltzmann方程的求解中方便地引入多种差分格式.

DBM被认为是Boltzmann方程的特殊离散形式,自然继承了Boltzmann方程可以用来描述非平衡效应的属性.在7个动力学矩关系(3)—(9)式中,只有前面3个动力学矩关系(质量、动能和能量的定义),可以被fi取代,而后面的4个动力学矩关系,如果用fi取代则两侧值会产生偏差.这个偏差从物理上来看是描述系统状态偏离热力学平衡所引起的宏观效应,可用于描述系统状态偏离热力学平衡的程度[22].本文考虑扣除宏观流动的微观粒子热涨落特征的热动非平衡效应,对应的中心矩定义如下:

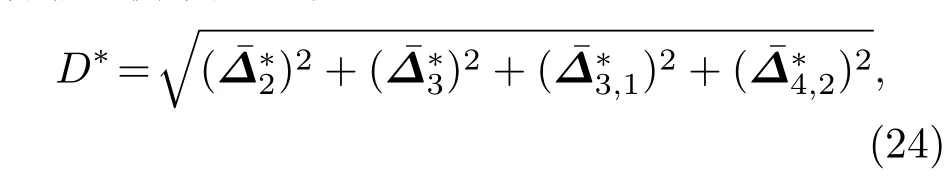
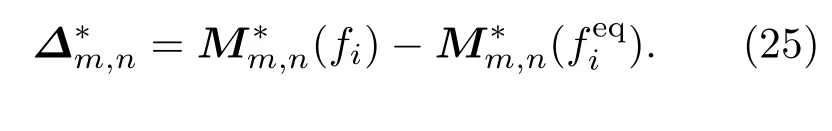
3 数值模拟与验证

本节通过一维Riemann问题:Sod激波管、冲击波碰撞和热Coutte流问题的解析解和数值解的符合程度来验证DBM的有效性.计算动理学方程(1)时,时间导数采用一阶向前差分,空间格式采用无波动无自由参数的耗散(non-oscillatory,containing no free parameters and dissipative,NND)格式[32].事实上,NND格式是二阶迎风格式、一阶迎风格式、中心差分格式的混合格式,该格式针对激波上下游采用不同的混合格式,其总变差(total variation diminishing,TVD)是减小的,空间上具有实质的二阶精度高分辨率,捕捉激波能力较强,可以很好地分辨间断.

3.1 Sod激波管问题

Sod激波管问题.计算区域 [−1,1],流场的左半部分和右半部分分别给定如下的初始条件:

其中“L”和“R”分别代表远离间断界面左右两侧的宏观量初始值.计算网格为Nx×Ny=2000×2,空间步长为 ∆x=∆y=0.001,时间步长选取为∆t=10−5.其他模型参数选取为τ=10−5,n=3,c=1.0和η=10.0.y方向采用周期边界条件,对于x方向,左边界设置为

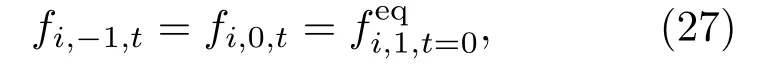
其中−1和0表示左边的虚拟点.此类边界条件指定系统在边界处一直处于平衡态,即边界处的宏观量为

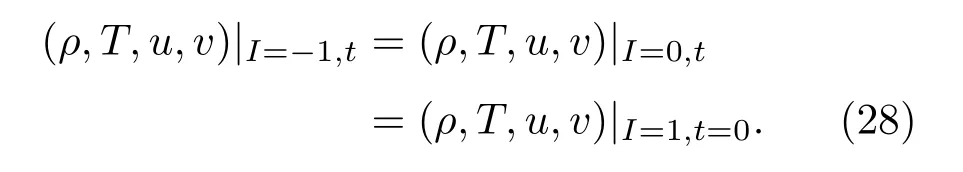
方程(27)和(28)也被称作微观和宏观边界条件,两者是互相对应的.

同样,右边的微观边界设置如下:

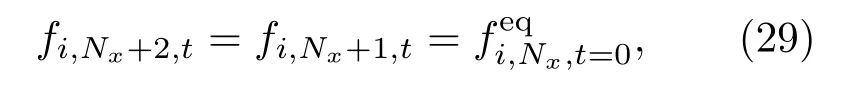
则对应的宏观边界为

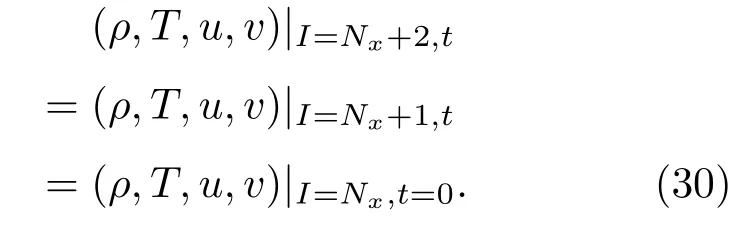
为验证网格无关性,先固定其他模型参数,x方向采用三种不同的网格数:Nx=1000,2000,4000,模拟结果见图1.可见,三种不同空间分辨率都能够清晰捕捉激波、接触间断和稀疏波.采用Nx=2000的模拟结果与采用Nx=4000的模拟结果区别不大.为了更好地展示该物理问题不同物理量的非线性间断结构,图2给出DBM数值解与解析解在t=0.2的对比图,图中圆圈为DBM 数值解,直线为精确解.结果显示,DBM数值解与解析解符合较好,验证了模型的准确性和健壮性.

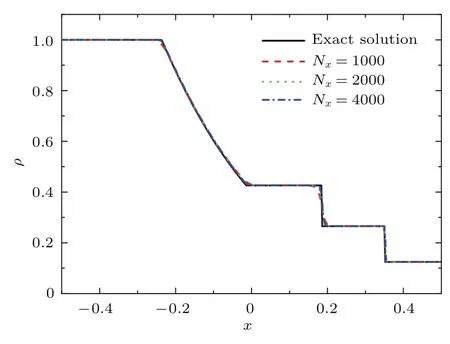
图1 不同网格数下t=0.2时刻一维Sod激波管密度剖面的DBM数值解与解析解对比Fig.1. Comparisons between DBM results with dif f erent grids and the exact solution for the onedimensional Sod problem,at t=0.2.

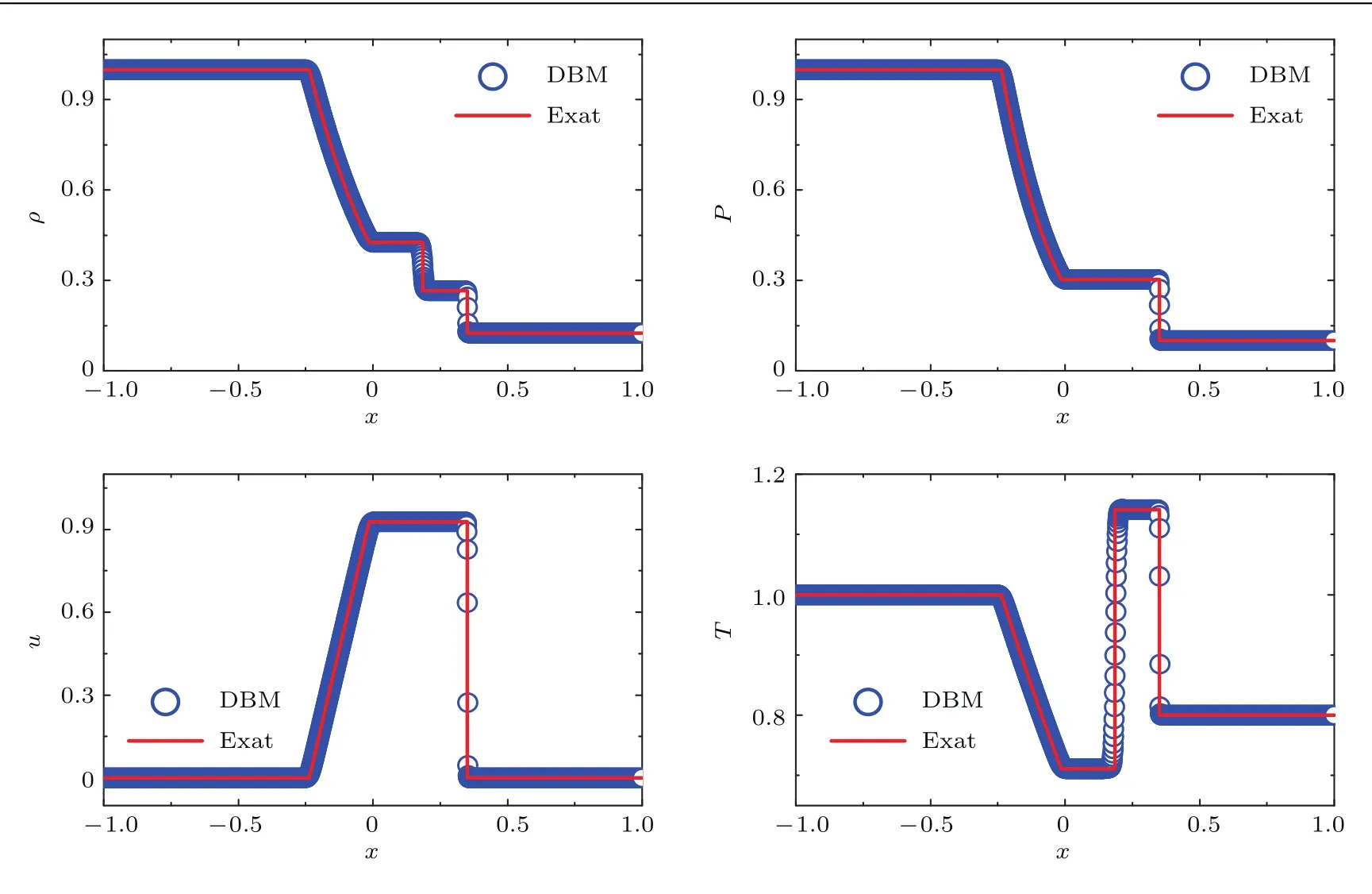
图2 t=0.2时刻一维Sod激波管的密度、压力、速度和温度剖面的DBM数值解与解析解的对比Fig.2.Comparisons between DBM results and the exact solutions for the one-dimensional Sod problem at t=0.2.

3.2 两个强激波碰撞问题

为了充分验证模型,考虑冲击波碰撞问题,该问题涉及两个强激波的碰撞,其初始条件为:

该问题的精确解包含了一个缓慢向右传播的左激波、向右的接触界面和一个左行激波.其中,左激波向右传播很慢给数值方法带来额外的困难,对模型的稳定性和鲁棒性要求较高.

数值模拟中,选取参数为：网格参数为Nx×Ny=2000×2,∆x= ∆y=0.003,时间步长为∆t=10−5.其他参数选取为τ=2×10−5,n=3,c=8.0和η=40.0.图3给出了t=0.08时刻γ=1.4的密度、压力、速度和温度剖面的DBM数值解与解析解的对比.对比结果表明,DBM数值解与解析解符合较好,进一步说明DBM模型具有较好的稳定性和鲁棒性.

3.3 热Coutte流问题

作为经典热传导问题,热Coutte流能够用来检测DBM模拟流体黏性热传导问题.该问题描述如下:考虑介于两个无限长平行板之间的黏性流体,平板之间距离为H.初始条件为(ρ,u,v,T)|t=0=(1.0,0,0,1.0).当t>0 时,温度为T0的上板以速度u0=0.8移动,温度为T0的下板保持静止不动.

网格参数选取为Nx×Ny=1×200,空间步长为∆x=∆y=2×10−3,其他参数选取为:n=3,τ=10−3,c=1.0,η=10.0,∆t=10−5.x方向采用周期边界条件,y方向采用非平衡外推格式[33].

x方向速度的解析解为

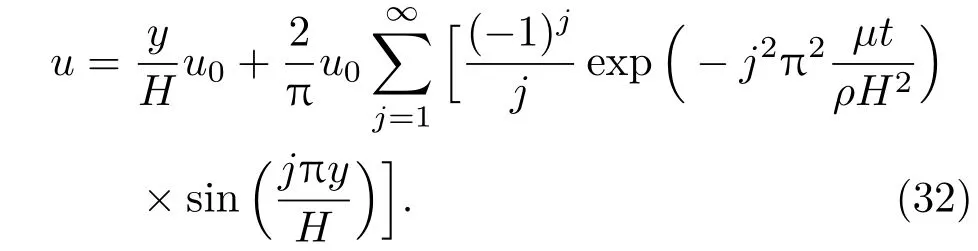
图4给出了DBM数值解与解析解在不同时刻的对比图,两者十分符合,表明DBM能够精确计算黏性耗散下的流体问题.计算结果与NS模型得到的结果一致.

当系统达到稳态时,沿y方向温度场的理论解为

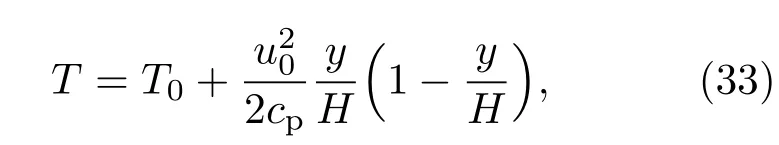
其中cp=γ/(γ−1).图5展示了不同γ对应的DBM数值解与解析解在稳态时的对比图.数值解与解析解符合较好,表明DBM能够精确模拟不同热传导情形下的流体问题.

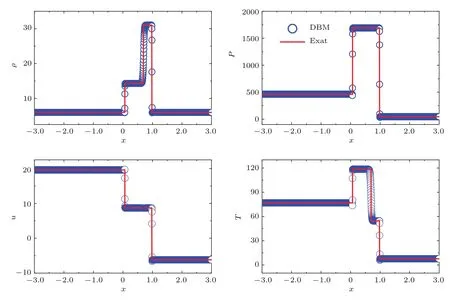
图3 t=0.08时刻两个强激波碰撞问题的密度、压力、速度和温度剖面的DBM数值解与解析解对比Fig.3.Comparisons between DBM results and the exact solutions for collision of two strong shocks problem at t=0.08.

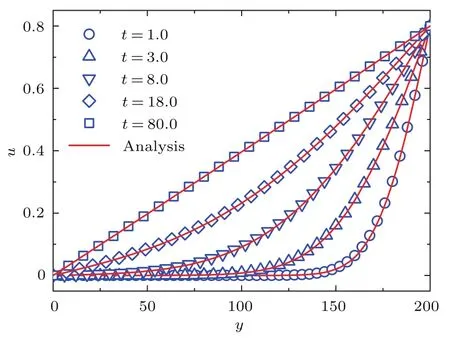
图4 γ=1.4时热 Couette流在不同时刻速度剖面的DBM数值解与解析解对比Fig.4.Comparisons between DBM results and the exact solutions for the velocity profiles in thermal Couette flow for the case with γ=1.4 at various times.

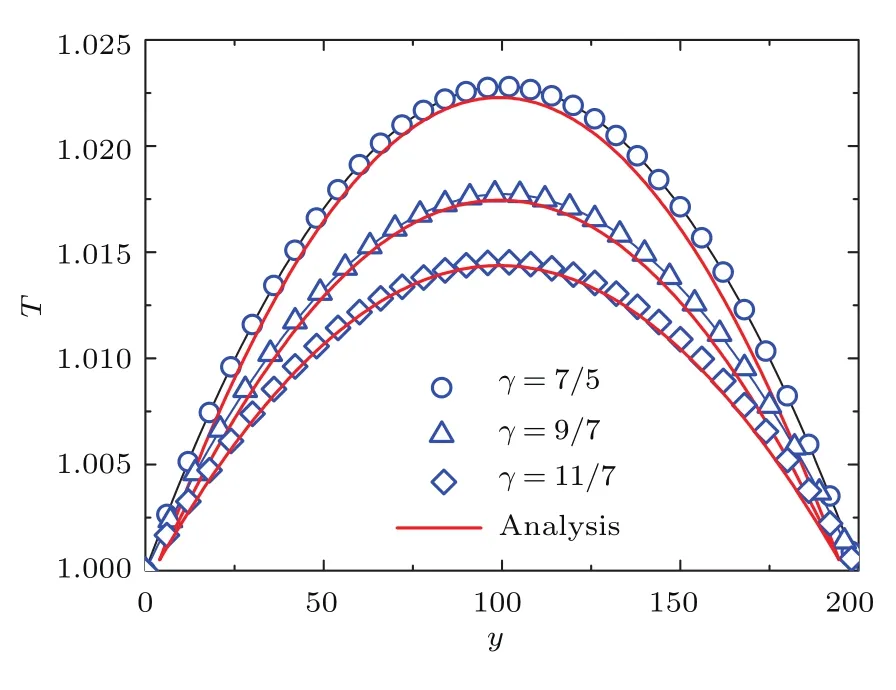
图5 不同γ值下热Couette流的稳态温度剖面的DBM数值解与解析解对比Fig.5.Comparisons between DBM results and the exact solutions for the temperature profiles in steady thermal Couette flow for various values of γ.

4 可压流体RT不稳定性数值模拟

对于RT不稳定性的数值模拟,以往模型主要采用等温不可压模型,即上下密度是常数而温度始终不变的情形,而实际系统往往是可压的且温度是变化的.本文考虑单介质流体的可压非等温情形,即温度自适应情形.该流体系统由上下两部分组成,上下温度不同,系统密度满足力学平衡条件呈指数分布[16−27].例如,考虑上流体是冷空气下流体是热空气.当中间界面处没有发生扰动,则系统只有热扩散作用,界面始终处在中间位置.当中间界面出现小扰动之后,由于重力的作用,扰动会随着时间的演变而慢慢放大,形成“气泡-尖钉”结构,而后出现典型的“蘑菇头”形状,即RT不稳定性发生.在数值模拟过程中,边界影响比较大,本文采用如下边界条件:上下边界采用绝热、无滑移边界条件;左右采用周期边界条件.模型从最简单的理想气体状态方程出发,暂时忽略表面张力的影响.

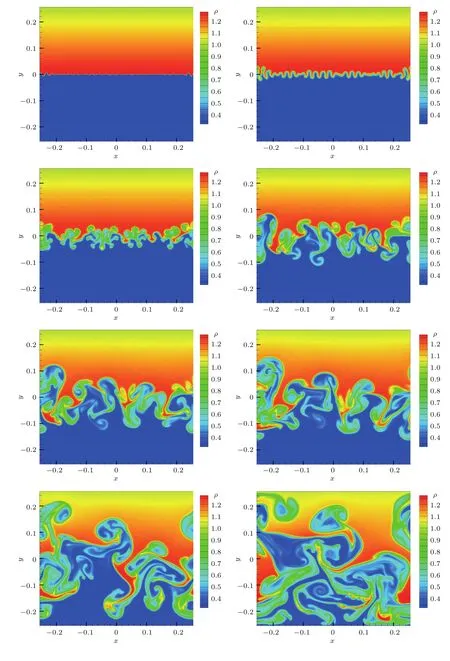
图6 多模RT不稳定性在不同时刻的密度演化图:t=0,0.5,1.0,1.5,1.8,2.0,2.5,3.0Fig.6.Density evolution of Rayleigh-Taylor instability from a multiple mode perturbation at dif f erent times:t=0,0.5,1.0,1.5,1.8,2.0,2.5,3.0.

本文考虑二维区域 [−d/2,d/2]×[−2d,2d],系统处于重力加速度为常数的重力场下,界面的初始扰动满足

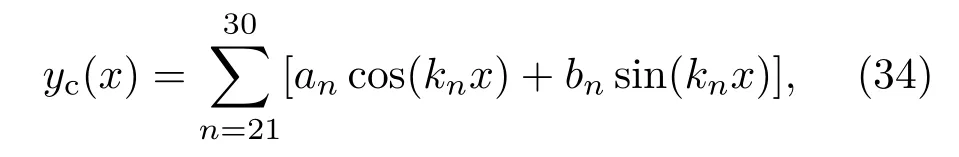
其中kn=2nπ/Lx,an,bn是 0—1之间均匀分布的随机数.上下部分流体的温度不同,每部分流体的密度分布满足如下静力学平衡条件:

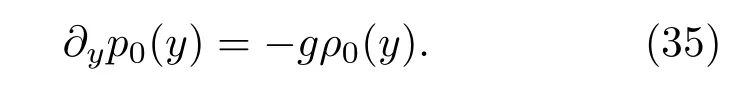
所以系统的不稳定性初始条件满足:

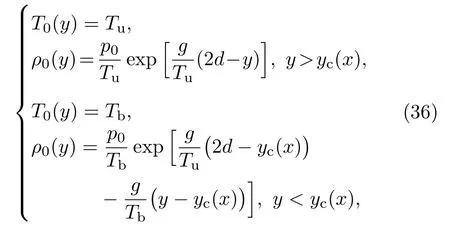
其中,p0是上部分流体顶部的初始压强,Tu和Tb代表上下部分流体的初始温度.在这种条件下,界面处的压强满足

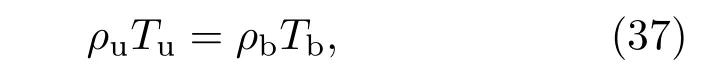
其中ρu和ρb是上下部分流体临近界面两侧网格处的密度,则界面处初始Atwood数可以定义为[16]

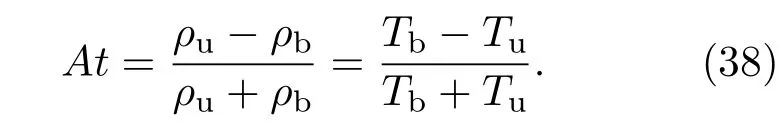
在数值模拟中,计算区域为512×512的均为网格,空间步长为∆x=∆y=0.001,顶部初始压强为p0=1.0,时间步长为 ∆t=1×10−5,松弛因子为τ=1×10−5,上部分温度为Tu=1.0,下部分温度为Tb=4.0,因此,初始At=0.6.其他参数为c=1.3,η=15,n=3,ax=0.0,ay=−g=−1.0.

图6展示了RT不稳定性的密度分布随时间变化的时空演化图,可以看出,初始阶段,热扩散作用迅速抹平了间断界面,产生有限宽度的过渡层,降低了界面处局部At数.经过短暂的线性阶段,RT不稳定性进入了非线性阶段.在重力场的作用下,随着时间的发展,重流体下降,轻流体上升,又由于重流体相对较“硬”,轻流体相对较“软”,因而呈现典型的“气泡”和“尖钉”的界面结构.之所以形成这种结构,是因为当密度较大时,惯性力较大,较难改变速度,从而向上的扰动形成较平的“气泡”结构,向下的扰动形成较尖锐的“尖钉”结构.后期由于界面切向速度差变大(即KH不稳定性慢慢起作用),“尖顶”尾部翻转起来,形成“蘑菇头”形状.由于热扩散和黏性作用,“蘑菇头”尾部渐渐模糊且变狭长.事实上,一开始(t=0.5之前)演化较慢,且界面整体下移,这是由于一开始热传导起主导作用,在界面附近的上下流体交换内能,上流体吸收热量,体积膨胀,界面附近的上流体下移,而下流体释放热量,体积缩小,界面附近的下流体下移.同时,初始多模互相竞争合并,模式慢慢变少,界面被“抹平”;而后(t=0.5)之后演化加速,界面演化变成重力主导,上下流体开始以交换重力势能为主,呈现非线性演化阶段.后期两流体在界面附近相互渗透,相互混合,进入湍流混合阶段.

图7展示了在不同初始多模扰动下总平均热动非平衡效应的演化情形.由于初始条件处于热动非平衡,系统有趋于热动平衡态趋势,D∗有下降的趋势.而后,随着模式的耦合以及混合层厚度不断增加,界面越来越复杂,系统偏离热动平衡态的演化以线性形式增长.而后,在t∗=0.7后系统趋向平衡态,t∗=1.2后系统又慢慢远离平衡态,这是因为系统重力势能和压缩能得到释放,部分转化为动能,促进了RT不稳定性的发展,界面越来越复杂,非平衡模式越来越丰富.

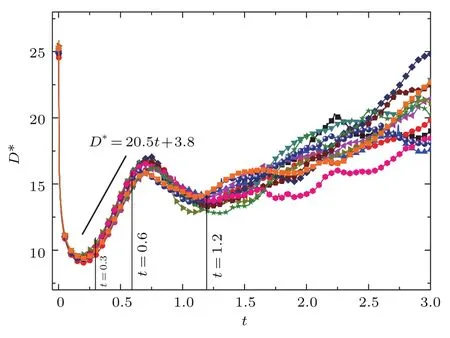
图7 不同初始多模扰动下RT不稳定性演化引起的总平均热动非平衡效应随时间的演化Fig.7.The time evolution of the global average TNE strength due to Rayleigh-Taylor instability with different multi-mode initial conditions.

5 结 论

应用含外力项的DBM数值模拟研究可压流体多模初始扰动的RT不稳定性问题.Chapman-Enskog多尺度分析表明该模型在连续极限可恢复到Navier-Stokes方程.模型通过了热Coutte流问题和三个一维Riemann问题的检测,表明模型能够精确模拟黏性耗散和热传导以及复杂激波之间的相互作用.采用DBM对多模、可压、具有间断界面的多模初始扰动RT不稳定性进行数值模拟.结果表明,在RT不稳定性发展的初期由于多模的设置,界面处的黏性和热传导效应突出,这些耗散效应会“抹平”界面,多模之间相互竞争和吸收,形成较少的主导模式;在这一阶段系统内没有形成明显的“气泡”和“尖钉”结构.在RT不稳定性的中后期,由于模式的合并导致界处的耗散效应减弱,重力占主导地位,扰动界面逐渐变形、长大,形成典型的“气泡-尖钉”结构,即出现典型的“蘑菇头”形状,而后进入湍流混合阶段.这些现象与经典的实验结果一致.同时给出系统整体非平衡程度随时间发展的演化情况,一开始系统先趋于平衡态,这是由于系统处于调整阶段,从多模初始界面扰动调整到本征模阶段;而后系统以线性形式偏离平衡态,这是由于系统界面被抹平,压缩能部分转化为内能;然后系统又趋于平衡态,这是由于模式的耦合与扰动界面进一步被“抹平”,系统处于相对稳定状态;最后系统越来越远离平衡态,此时是由于系统轻重流体的重力势能相互转换,系统的压缩能进一步被释放出来,系统动能进一步增加所致.在最近的一系列学术报告中,许爱国等[34−37]进一步给出了非平衡程度更深、超越Navier-Stokes描述能力的复杂流动系统的DBM建模思路.

[1]Rayleigh L 1882Proc.London Math.Soc.s1-14 170

[2]Lamb H 1932Hydrodynamics(6th Ed.)(London:Cambridge University press)p501

[3]Taylor G 1950Proc.R.Soc.London A201 192

[4]Betti R,Goncharov V,McCrory R,Verdon C 1998Phys.Plasmas(1994–present)5 1446

[5]Wang L F,Ye W H,Wu J F,Liu J,Zhang W Y,He X T 2016Phys.Plasmas23 052713

[6]Wang L F,Ye W H,He X T,Wu J F,Fan Z F,Xue C,Guo H Y,Miao W Y,Yuan Y T,Dong J Q,Jia G,Zhang J,Li Y J,Liu J,Wang L M,Ding Y K,Zhang W Y 2017Sci.China:Phys.Mech.Astron.60 055201

[7]Cabot W,Cook A 2006Nat.Phys.2 562

[8]Berthoud G 2000Annu.Rev.Fluid Mech.32 573

[9]Barber J L,Kadau K,Germann T C,Alder B J 2008Eur.Phys.J.B64 271

[10]Celani A,Mazzino A,Vozella L 2006Phys.Rev.L.96 134504

[11]Moin P 1991Comput.Meth.Appl.Mech.Eng.87 329

[12]Succi S 2001The Lattice Boltzmann Equation for Fluid Dynamics and Beyond(New York:Oxford University Press)pp179–255

[13]He X Y,Chen S Y,Zhang R Y 1999J.Comput.Phys.152 642

[14]Li Q,Luo K H,Gao Y J,He Y L 2012Phys.Rev.E85 026704

[15]Liu G J,Guo Z L 2013Int.J.Numer.Method H.23 176

[16]Scagliarini A,Biferale L,Sbragaglia M,Sugiyama K,Toschi F 2010Phys.Fluids22 055101

[17]Xu A G,Zhang G C,Gan Y B,Chen F,Yu X J 2012Front.Phys.7 582

[18]Xu A G,Zhang G C,Gan Y B 2016Mech.Eng.38 361(in Chinese)[许爱国,张广财,甘延标2016力学与实践38 361]

[19]Gan Y B,Xu A G,Zhang G C,Yu X J,Li Y J 2008Physica A387 1721

[20]Gan Y B,Xu A G,Zhang G C,Li Y J 2011Phys.Rev.E83 056704

[21]Gan Y B,Xu A G,Zhang G C,Li Y J,Li H 2011Phys.Rev.E84 046715

[22]Yan B,Xu A G,Zhang G C,Ying Y J,Li H 2013Front.Phys.8 94

[23]Xu A G,Zhang G C,Li Y J,Li H 2014Prog.Phys.34 136(in Chinese)[许爱国,张广财,李英骏,李华2014物理学进展34 136]

[24]Xu A G,Zhang G C,Ying Y J 2015Acta Phys.Sin.64 184701(in Chinese)[许爱国,张广财,应阳君2015物理学报64 184701]

[25]Xu A G,Zhang G C,Ying Y J,Wang C 2016Sci.China:Phys.Mech.Astron.59 650501

[26]Lin C D,Xu A G,Zhang G C,Li Y J,Succi S 2014Phys.Rev.E89 013307

[27]Lai H L,Xu A G,Zhang G C,Gan Y B,Ying Y J,Succi S 2016Phys.Rev.E94 023106

[28]Liu H,Kang W,Zhang Q,Zhang Y,Duan H L,He X T 2016Front.Phys.11 115206

[29]Gan Y B,Xu A G,Zhang G C,Yang Y 2013Europhys.Lett.103 24003

[30]Gan Y B,Xu A G,Zhang G C,Succi S 2015Soft Matter11 5336

[31]Watari M,Tsutahara M 2004Phys.Rev.E70 016703

[32]Zhang H X 1988Acta Aerodyn.Sin.6 43(in Chinese)[张涵信1988空气动力学学报6 43]

[33]Guo Z L,Zheng C G,Shi B C 2002Phys.Fluids14 2007

[34]Xu A G,Zhang G C 2016The 9th National Conference on Fluid MechanicsNanjing,China Oct.20–23,2016(in Chinese)[许爱国,张广财2016第九届全国流体力学学术会议,南京,2016年10月20—23日]

[35]Xu A G,Zhang G C 2016Special Academic Report of Electromechanical College of Nanjing Forestry UniversityNanjing,China,Oct.25,2016(in Chinese)[许爱国,张广财2016南京林业大学机电学院专题学术报告,中国南京,2016年10月25日]

[36]Xu A G,Zhang G C 2016Academic Report on Physics Department of Renmin University of ChinaBeijing,China,Nov.23,2016(in Chinese)[许爱国,张广财 2016中国人民大学物理系专题学术报告,中国北京,2016年11月23日]

[37]Xu A G,Zhang G C 2016The 4th Academic Seminar of LBM and Its ApplicationsBeijing,China,Nov.26,2016(in Chinese)[许爱国,张广财 2016第四届LBM及其应用学术研讨会,中国北京,2016年11月26日]