基于多时间粒度的地铁出行规律相似性度量
2018-05-07张晚笛王子甲
张晚笛 , 陈 峰,2 , 王子甲 , 汪 波, 王 挺
(1.北京交通大学 土木建筑工程学院,北京 100044; 2.北京交通大学 北京市轨道交通线路安全与防灾工程技术研究中心,北京 100044; 3. 北京市交通信息中心,北京 100073)
乘客出行规律性体现在网络、线路、区间以及车站四个层级的客流特征上。掌握不同层级的客流规律对城市轨道交通规划、运营管理均具有重要意义,尤其在网络化运营背景下,要求客流监管更精细化,组织策略更加智能化和动态化,因此挖掘较低层级的短时客流规律,才能满足网络化运营需求。在观测短时客流规律时,选择的时间粒度大小以及观测时间段均会对观测结果产生较大影响。例如观测车站层级历史同期(不同天的同一时段,如周一和周二的上午8点至9点,上周一和本周一的上午8点至9点,本文中主要指后者)的进站客流规律,选择15 min、60 min或1天的时间尺度,观测得到的规律会有较大差异;观测历史同期车站OD客流规律时,不同时间粒度下高峰和平峰的规律性也会有所不同。因此,本文以相似性作为客流规律的量化指标,在车站层级研究历史同期进站客流和OD客流随时间粒度的变化规律,对辅助运营决策、安全高效完成运输任务以及指导短时客流预测的时间粒度选择或方法改进均具有重要意义。
目前的短时客流规律研究以客流预测为主,且多侧重改进预测方法以提升短时预测精度,文献[1-2] 使用单一模型对车站单一时间粒度的进站客流进行预测。文献[3]使用组合方法对车站单一时间粒度的进站客流进行预测。也有少量研究从预测结果后评估的角度分析工作日和周末高峰、平峰预测的差异[4-5],以及不同时间粒度下预测结果的差异[6-8]。从已有研究可以看出,使用组合方法在一定程度上提高了预测精度,从预测后评估的角度也证实时间粒度大小和预测时段对精度影响较大,但在预测前对车站历史同期客流相似性规律进行充分挖掘的研究较少。车站进站客流和OD客流在多大时间粒度下规律性较强?是否所有车站在所有时段的短时客流均是可预测的?对此,本文从历史同期进站客流和OD客流相似性度量出发,充分挖掘客流随时间粒度变化的波动规律,找出客流出现较强规律的最小时间粒度和时间段,对全网车站可预测性等级进行划分,以期对短时客流预测工作提供改进方向和思路。
1 数据和方法
时间序列是与时间相关的高维数据,在科学、工程、经济、社会等各个领域中广泛存在[9-11]。在时间序列挖掘的诸多任务和问题中,时间序列的相似性是最基础的问题[12], 大部分时间序列数据挖掘技术的初始工作都需要进行相似性比较,以便建立数据之间的二元关系,包括如何判别时间序列是否相似、如何衡量相似程度等。
相似性度量是衡量不同对象之间相互关系的方法。时间序列的相似性常用距离来衡量,距离越小,两个时间序列的相似度就越高。本文通过构建不同时间粒度下的客流时间序列模型,分析客流时间序列之间的相似程度及累计相似性,对不同时间粒度下的客流规律性进行分析,评价客流的可预测性。
本研究选取2016年3月和4月连续五周的北京地铁自动售检票系统(AFC)数据,以周一、周三、周五和周日为工作日与双休日的特征天进行研究,目的在于通过度量历史同期(同特征天、同时段)的地铁车站进站客流和OD客流相似性,挖掘多时间粒度下车站层级的客流规律。研究思路如图1所示。
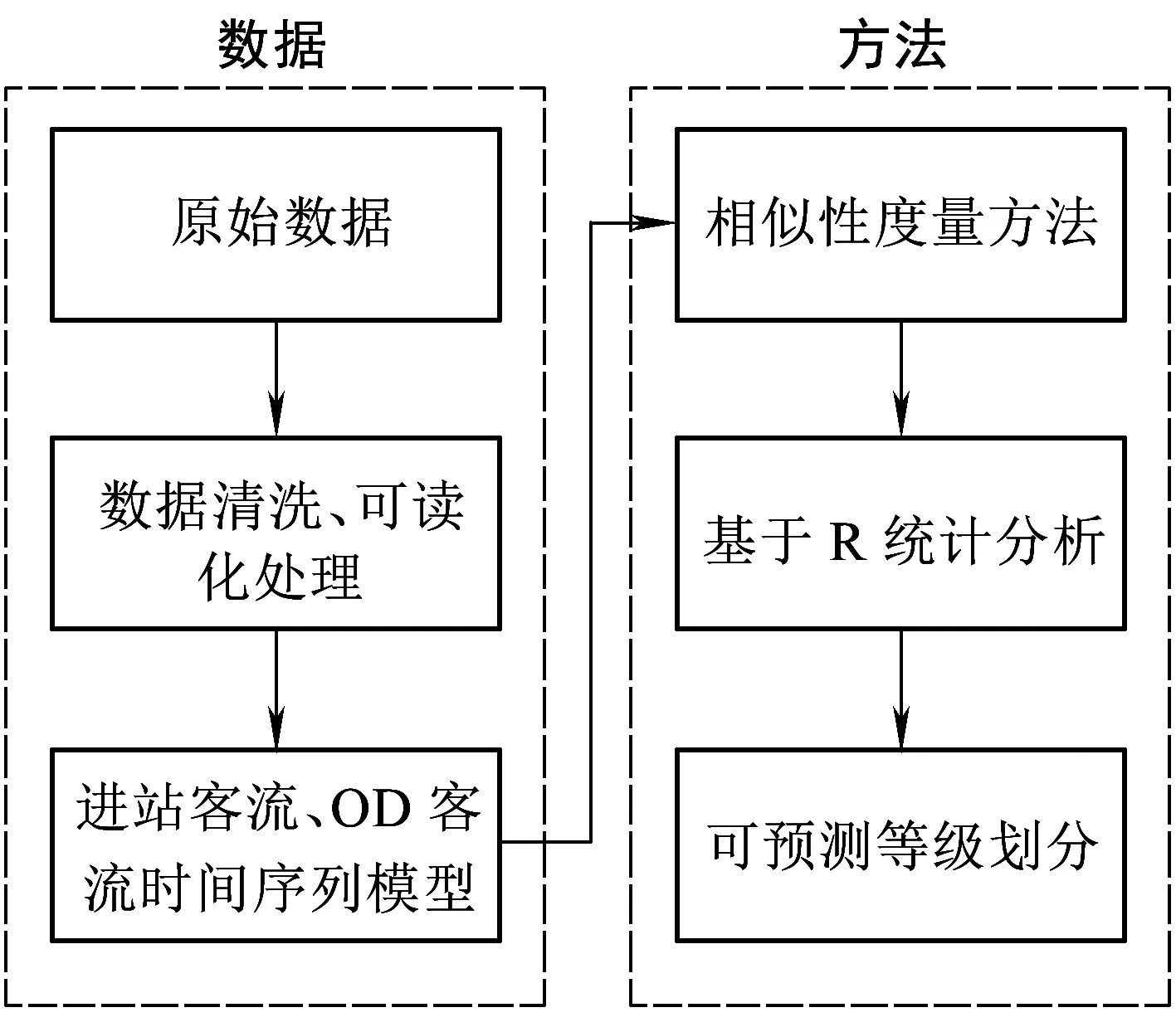
图1 研究思路流程
1.1 数据描述
AFC记录了使用一卡通出行乘客的卡号、进出站时间以及进出站站点等详尽的出行信息。北京地铁全网使用一卡通出行的乘客比例约85%,AFC提供的海量刷卡数据为研究乘客出行规律提供了数据基础。
如图1所示,对原始AFC数据清洗后,进一步可读化处理为客流时间序列,提取算法可识别的数据结构。本研究主要对进出站站点和进出站时间进行转换,表1为清洗后3月某日AFC数据可读化处理示例。2016年北京地铁共278个车站(换乘站不重复统计),因此将进站和出站站点转换为车站对应的编号(1~278)。每个特征天有1 440 min,将进站和出站时间(格式为YYYYMMDDHH24MISS)转换为对应的时间序号(1~1 440),基于以上可读化处理,设计算法提取不同时间粒度的进站客流和OD客流时间序列。
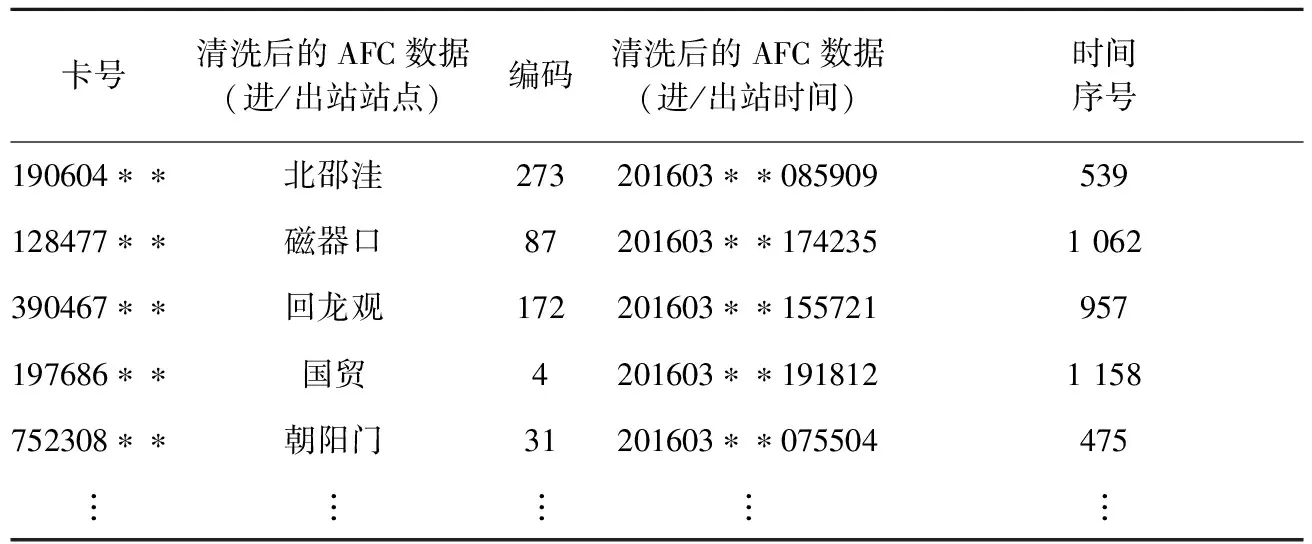
表1 AFC数据可读化处理示例
1.2 客流时间序列建模
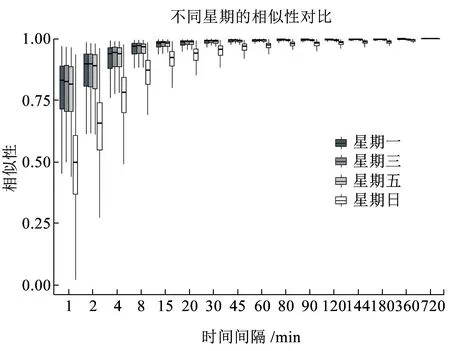
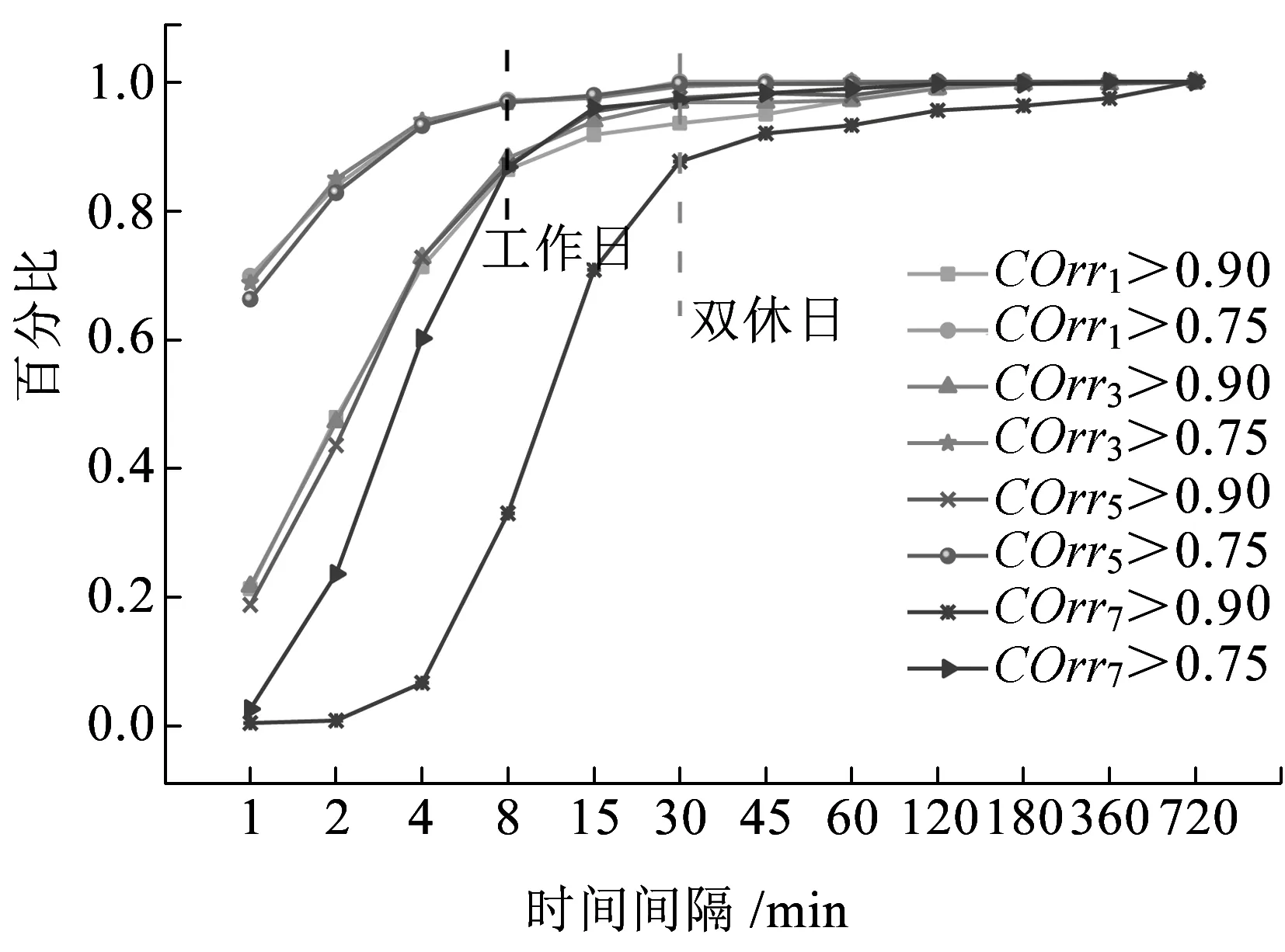
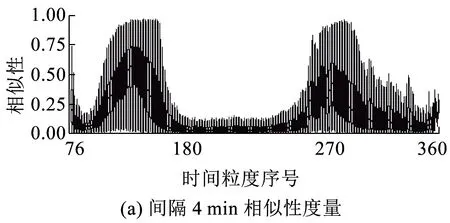
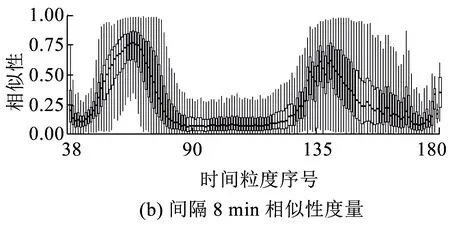
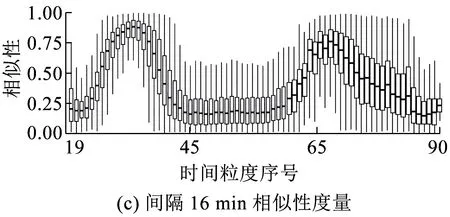
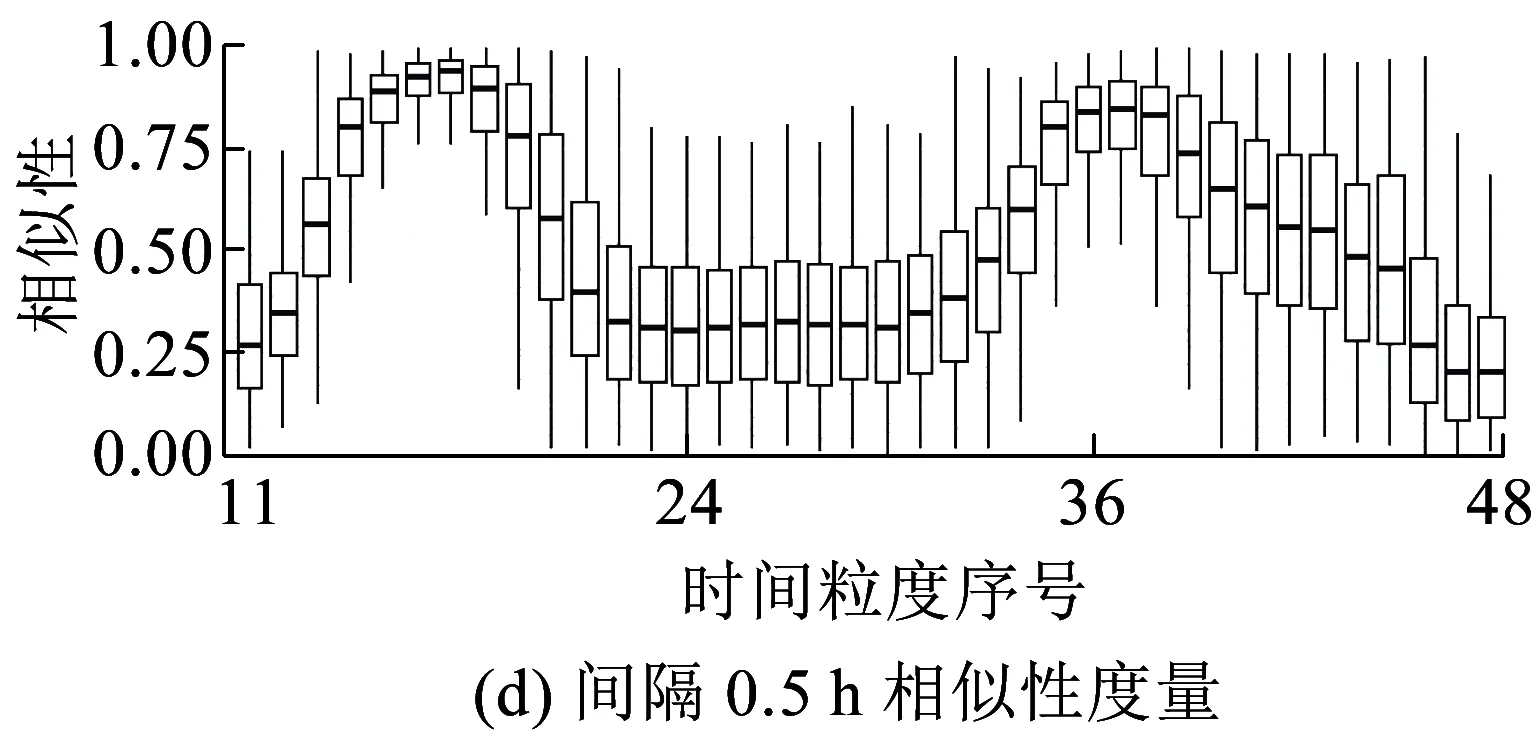
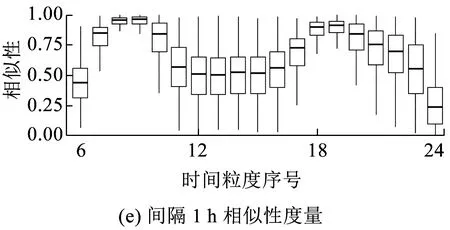
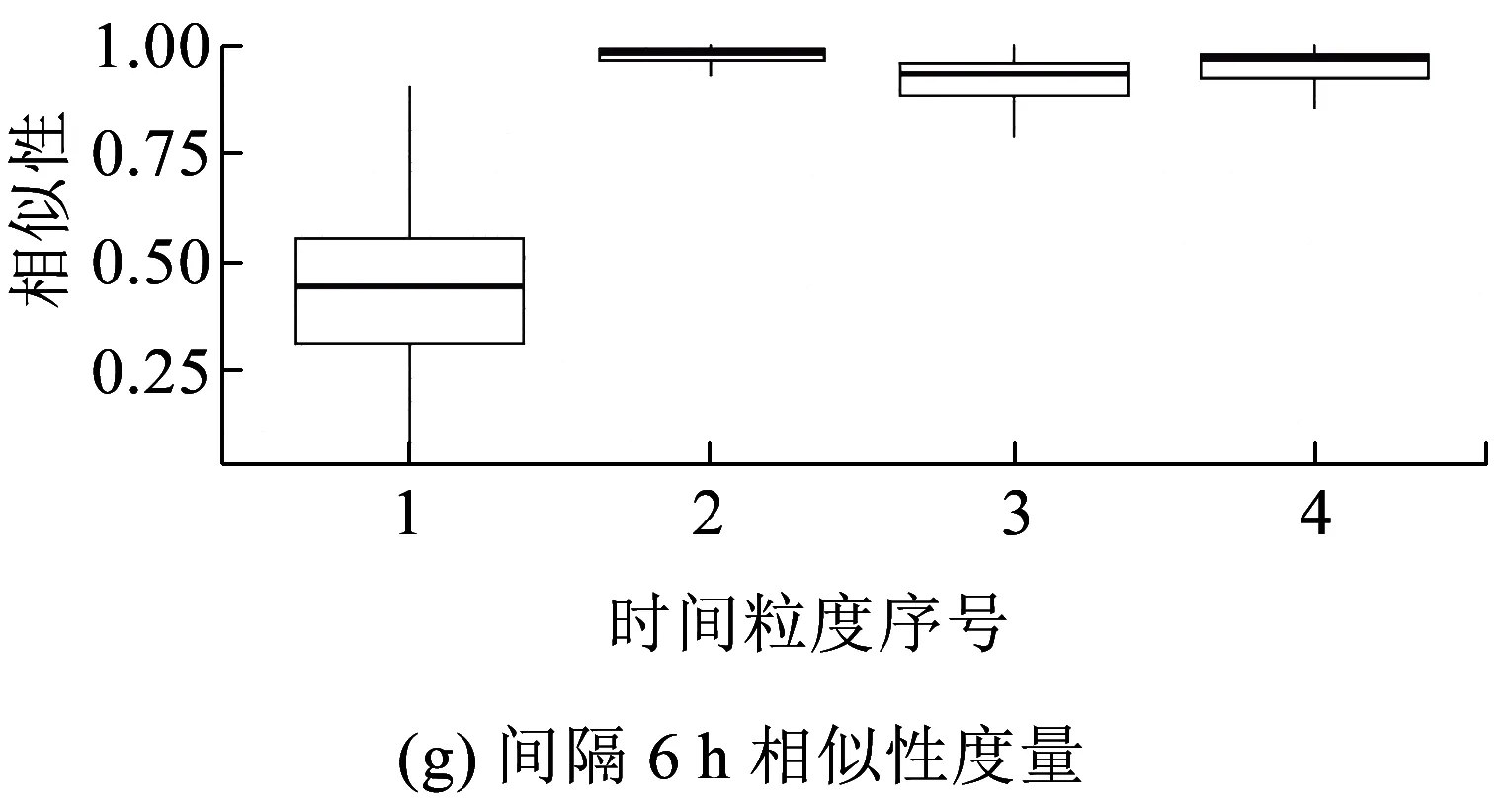
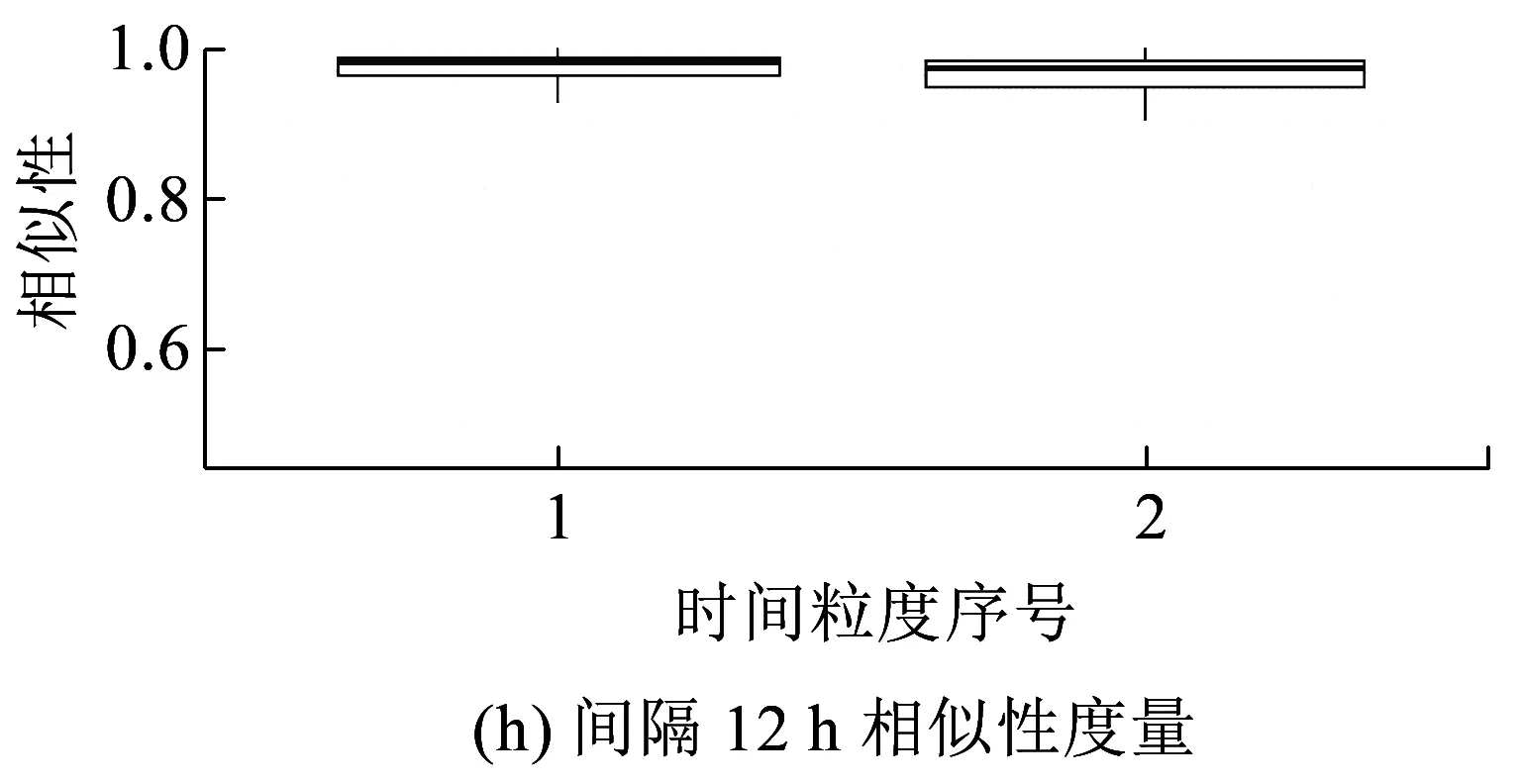
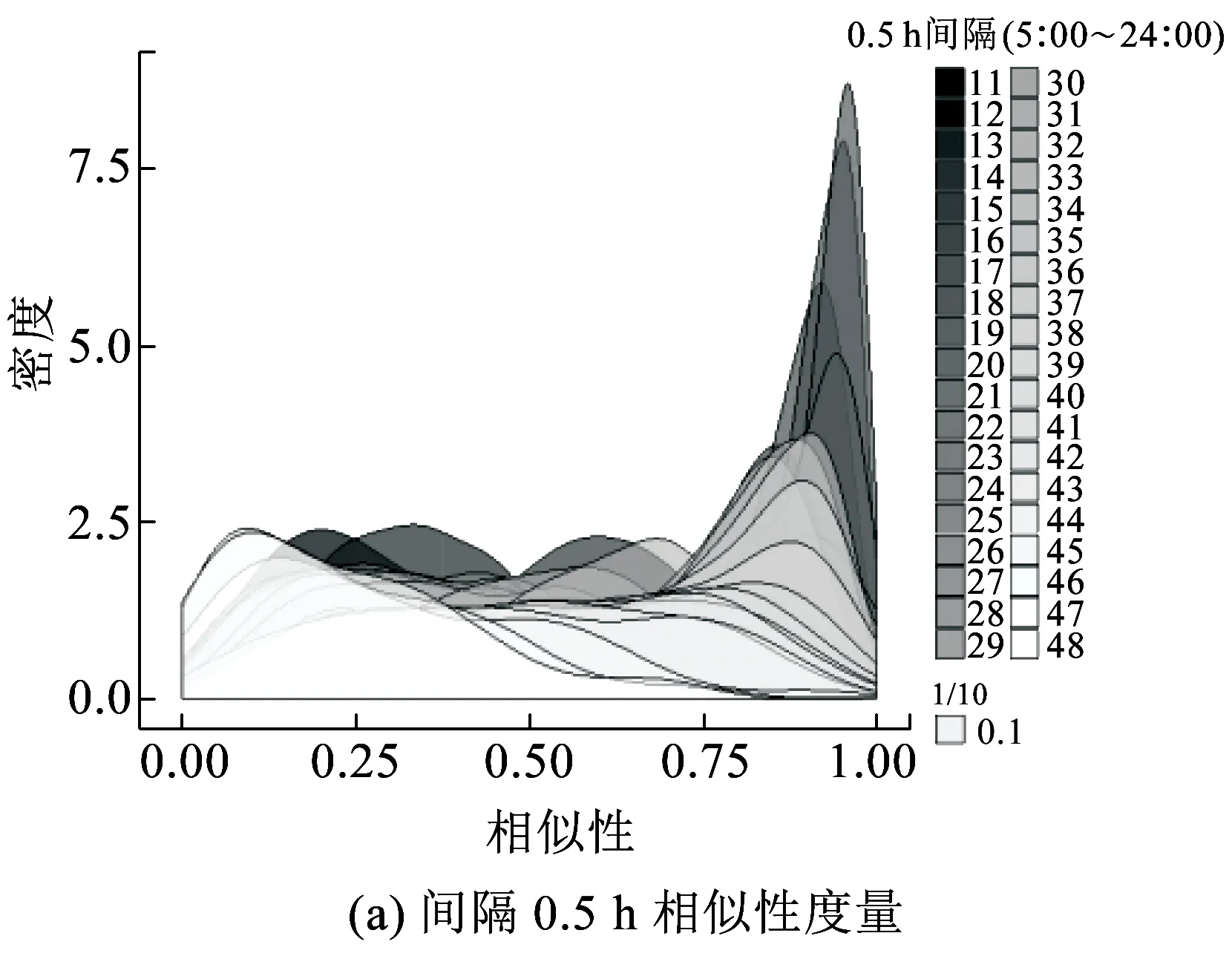
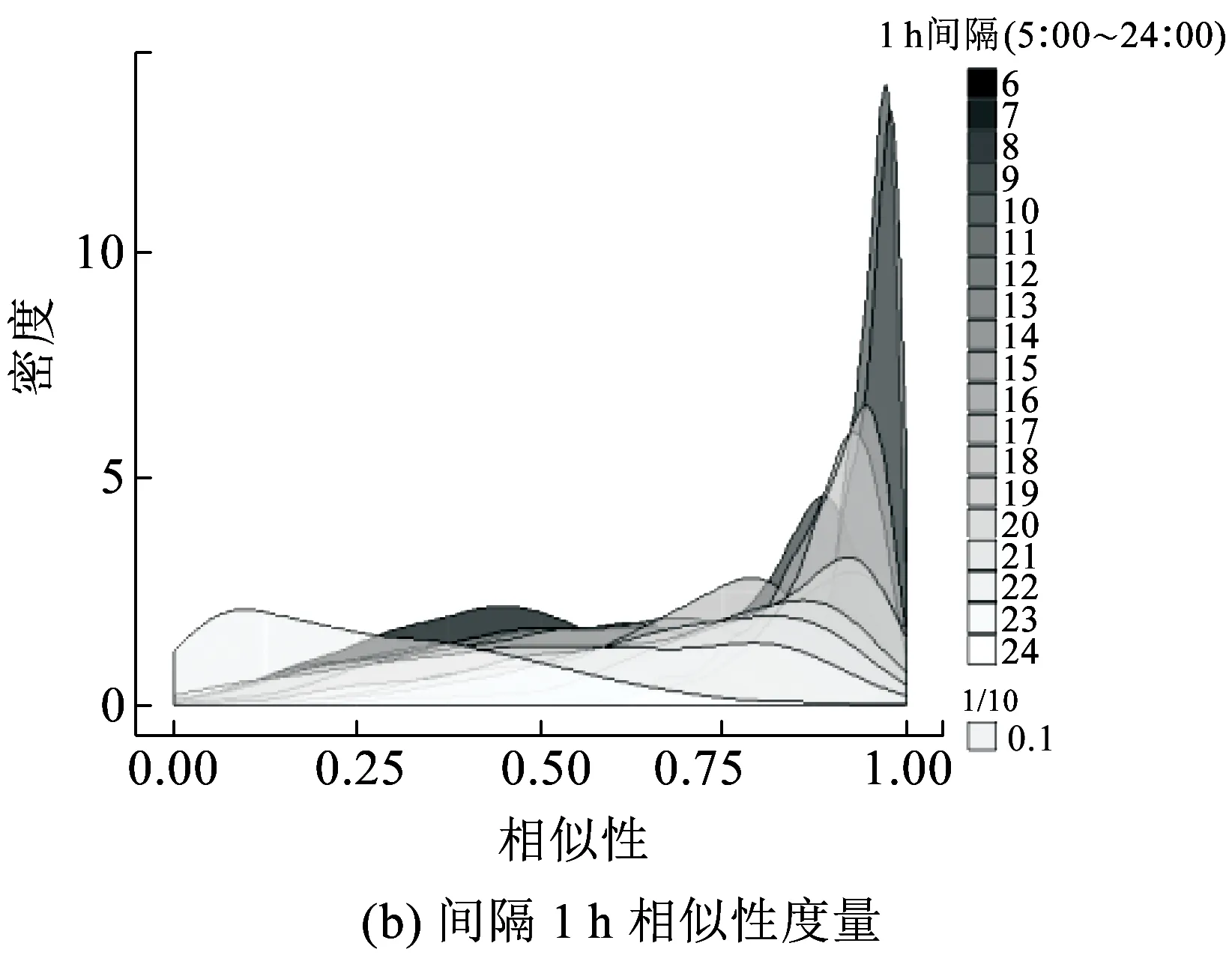
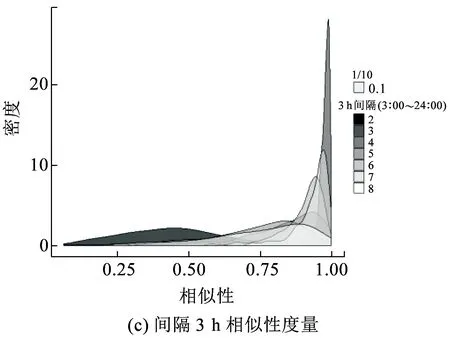
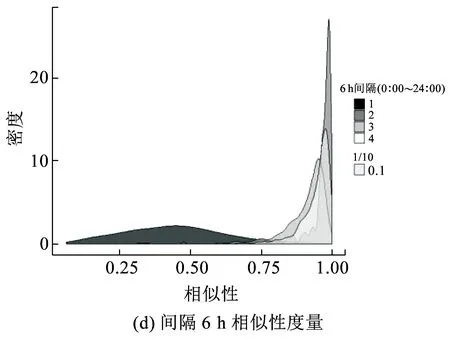
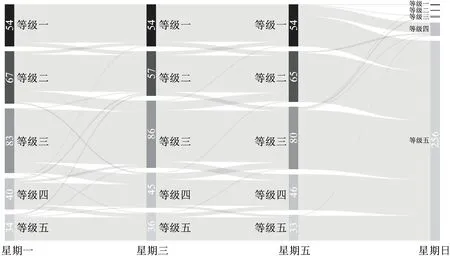
长度为n的时间序列由一条包含n个元素的序列组成,时间序列记为Q=[(t1,p1) (t2,p2) … (tn,pn)],其中每个数据单元表示为一个二元数组(ti,pi),其中ti为时间变量,代表第i个时间点,pi为数据变量,代表第i时刻观测值的集合,反映数据单元的实际意义[13]。本研究满足ti 时间间隔Δt即为本研究选取具有代表性的时间粒度 Δt=[1 2 4 8 15 20 30 45 60 8090 120 144 180 360 720] ( 1 ) 其所对应的每天被分割的间隔数为 n=[1 440 720 360 180 96 7248 32 24 18 16 12 10 8 4 2] ( 2 ) (1)进站客流时间序列 用改进的时间序列模型描述地铁车站进站量,为了区分不同周、不同天的观测值,二元数组中的数据变量用序列xN表示车站进站量。 xN=[xN1(iD)xN2(iD) … xNt(iD) …xNn(iD)] (2)OD客流时间序列 除了车站进站客流外,车站之间的客流流动也是出行规律的重要研究内容。与车站进站客流时间序列类似,构建车站之间客流流动的时间序列模型,以Δti为时间粒度,研究每个时间粒度下车站N为出行起点或迄点的历史同期OD客流相似性。某个时间粒度下车站N去往其他车站和其他车站到达车站N的客流时间序列可用FN(iD)表示。 该矩阵是一个2M×n的矩阵,fN_t(iD)表示车站N在第i周第D天第t个时间段到全网其他车站(N→M)以及其他车站到车站N(M→N)的客流量。参数取值范围与进站客流时间序列模型相同。 目前用于度量时间序列相似性的方法包括欧式距离、动态时间弯曲距离、最长公共子串、概率距离、编辑距离、Pearson系数等。 本文利用Pearson系数度量客流时间序列的相似性,xN(iD)与xN(jD)的Pearson系数rN(iD,jD)可以表示为 ( 3 ) 车站N历史同期进站客流的累计相似性为 ( 4 ) l为度量的周数,在本研究中l=5。因此累计相似性COrrN_D_in∈(0,1)也是标准化的相似性。每周第D天每个Δti下全网车站进站客流的相似性度量结果是一个一维向量。 RΔt_D_in=[COrr1COrr2… COrrN…COrr278] ( 5 ) 累计相似性COrrN_D_t∈(0,1)也是标准化的相似性。星期D每个Δt下全网车站OD客流的相似性度量结果为一个278×n的矩阵。 车站层级的出行规律主要体现在时间与空间两方面,车站进站客流与OD客流时间序列充分反映了车站的时空特征。基于相似性度量模型,以连续五周北京地铁AFC数据为基础,分别对历史同期进站客流和OD客流的相似性进行度量。 基于不同天、不同时间粒度下车站进站客流时间序列的相似性度量结果,绘制箱图分析周一、周三、周五和周日的相似性规律。图2为时间粒度为1 min到720 min共16个间隔下全网278个车站的相似性变化规律。从整体变化趋势可以看出,随着时间粒度增大,车站历史同期进站客流相似度增加,表明在较大时间粒度下观测得到的客流规律更明显,且从每个时间粒度50%分位数看,增加趋势类似对数关系,这与选取的时间粒度大小类似指数增长有关;从单独一个特征天来看,不同车站历史同期的进站客流相似性差异较大,在较小时间粒度下这种差异更明显,因此在以历史同期客流为先验信息进行短时进站客流预测时,相似性较低的车站预测精度将相对较差;工作日与非工作日之间对比可以看出,同一时间粒度下工作日相似性高于周末,这是因为乘客在周末出行随机性较强,在一定时间段内统计的进站量会有较大差别。工作日中的周三相似性略高于周一和周五,因此工作日第一天与最后一天出行波动性比其他工作日大,而周中客流会相对稳定。 图2 进站客流相似性变化规律 历史同期进站客流相似性越高,其短时进站量可预测性越强,因此探索出现较强规律性的最小时间粒度对车站短时进站量预测具有重要意义。图3为不同时间粒度下进站客流相似性COrrD_in>0.90和COrrD_in>0.75的车站数量占全网车站总数的百分比。从图3可以看出,随着时间粒度增大,相似性大于0.90和0.75的车站占比不断增加。若以全网90%车站的相似性大于0.90为可预测性强弱的划分线,则工作日保证客流预测精度的最小时间粒度为8 min,周末的最小时间粒度为30 min。即在短时进站客流预测时,工作日选取8 min粒度,周末取30 min粒度,全网约90%的车站预测精度可达到0.90,增大预测的时间粒度,预测精度会进一步提升。 图3 车站进站客流可预测性的对比分析 图4 相似性在一天内不同时间粒度下的变化规律 以周三全网车站的OD客流相似性度量结果为例,图4分析了4 min到720 min共8个时间粒度下不同时间段的全网OD客流相似性变化规律。从每天的变化趋势可见相似性大小在不同时间段差异较大,呈现出高低峰的变化规律,且在较小时间粒度下表现较为明显,相似性较高的时间段也是全网出行的早高峰(7:00~9:00)和晚高峰(17:00~19:00),说明高峰期间的出行规律较强。对比不同时间粒度的OD客流相似性规律可以发现时间粒度越大,同时段的OD客流相似性越高,在较细的时间粒度下可以观测到更为细致、多样的相似性变化特征。 图5为全网车站在30 min、60 min、180 min和360 min粒度下不同时间段OD客流相似性的密度分布,从图5可以看出,包含出行高峰的相似性分布较为集中且接近1,早高峰相似性比晚高峰高,平峰时段相似性分布较为分散,如在30 min粒度下观测到分布最接近1且较集中的时间段为第14~18个间隔(7:00~9:00),其次为第34~38个间隔(17:00~19:00);此外,随时间粒度的增加,同一时间段观测到的相似性分布更为集中,如在180 min粒度下,观测第3个间隔(6:00~9:00)相似性分布的最高频数接近30,而在60 min粒度下,第6~9个间隔(6:00~9:00)的频数仅不到20。 图5 一天内不同时间段的相似性分布规律 车站历史同期的OD客流相似性越高,其短时OD可预测性也越强。为了更直观地展示全网车站在不同时间段和时间粒度下OD客流的可预测性,分别以COrrD_OD>0.90和COrrD_OD>0.75为阈值统计不同时间段的车站占比。图6纵坐标表示一个特征天被时间粒度分割的时间段,横坐标表示周一、周三、周五和周日,每天各有两个划分阈值。从图6的车站占比变化规律可以看出,随着时间粒度增加,相似性COrrD_OD>0.90和COrrD_OD>0.75的车站也不断增加,表明时间粒度越大,车站OD客流可预测性越强;观测一天不同时间段的比例可以发现早晚高峰的可预测性比平峰高,且早高峰比晚高峰可预测性强;不同天的规律相似性对比表明工作日可预测性远高于非工作日。因此,在较小的时间粒度下车站短时OD客流基本上是不可预测的,因为非工作日OD客流规律性不强,工作日平峰时段预测精度较差,即使是预测精度较高的早晚高峰期,最小时间粒度也要取60 min。 图6 多时间粒度下不同天车站OD客流可预测性对比 从上述分析发现不同车站在不同时间段与历史同期客流规律相似性差别较大,由此导致在短时客流预测时各车站的精度差异较大。综合车站短时进站量和OD量的相似性大小对车站短时客流可预测性进行分级,在为车站短时客流预测提供先验信息,以及针对不同等级车站改进预测方法等方面具有重要意义。 车站短时客流可预测性等级划分兼顾时间粒度和预测精度,即要求在较小的时间粒度下有较高的相似性,因此综合考虑短时进站客流和OD客流相似性,制定综合指标RΔt_N_D_C=min(RΔt_N_D_in,max(RΔt_N_D_OD)),其中时间粒度Δt∈{8,15,30,60},将全网车站划分为五个等级,划分标准如下: 等级一:可预测性最强,R8_N_D_C>0.9; 等级二:可预测性强,R8_N_D_C≤0.9&R15_N_D_C>0.9; 等级三:可预测性较强,R15_N_D_C≤0.9&R30_N_D_C>0.9; 等级四:可预测性较差,R30_N_D_C≤0.9&R60_N_D_C>0.9; 等级五:可预测性差,R60_N_D_C≤0.9。 同一车站在不同天是否具有相同的可预测等级也是车站客流规律的重要内容,图7为全网车站可预测等级的变化规律。从图7可以看出,同一车站在不同特征天的可预测性等级不一定相同,如星期一、星期三和星期五的等级一中均包含54个车站,但具体车站却不同;星期一到星期三,部分等级一车站降级为等级二,星期三到星期五,某些等级二和等级三的车站则升级为等级一;周末大部分车站都降级为等级五,即在60min时间粒度下都很难精确预测短时进站客流和OD客流。因此对不同天、不同等级的车站要采取适当的时间粒度才能得到较为精准的预测结果。 图7 不同天不同等级车站变化 图8 不同预测等级车站的空间分布 乘客出行规律与城市用地规划、经济水平、出行费用、气候条件等多种因素有关[14],轨道交通因为承担了大量通勤乘客的出行,因此客流分布规律受站点周边职住空间分布影响较大[15],车站客流与岗位居住人口比与呈现明显正相关[16]。不同预测等级车站的空间分布如图8所示,从图8可以看出,工作日可预测等级高的车站主要分布在城市外围和城市中心地区。城市外围车站周边多为居住用地,如5号线北端,八通线东端,昌平线、房山线沿线等,这些车站在工作日承担了大量通勤出行,客流组成性质单一,具有非常一致的“早进晚出”特征;城市中心可预测性等级较高的车站主要位于工作岗位密集的商业区,如国贸、西单、中关村等,而这类车站“早出晚进”的出行特征非常明显。此外,周边用地混合程度较高的车站乘客组成多样,没有特别一致的出行规律,可预测等级较低。周末乘客出行随机性强,出行目的多样,车站可预测等级普遍较低。由此可见,车站周边用地性质单一、客流组成单一的车站客流规律性较强,其可预测性等级相应较高,而车站周边用地性质混合度高,客流组成复杂,其可预测性等级相应较低。 本文基于连续五周的地铁AFC数据,提取车站进站客流和OD客流的时间序列,通过度量多时间粒度下历史同期客流时间序列的相似性大小,挖掘车站客流相似性大小随时间粒度的变化规律,根据综合的相似性指标对车站可预测等级进行划分。研究主要得到以下成果和结论: (1)构建了一套完整描述客流特征的时间序列模型和客流相似性度量的方法。该方法只需要乘客出行的起终点及时间信息,而AFC数据一般都包含乘客的卡号、进出站站点和进出站时间字段,因此该模型方法具有一定的普适性,可以推广到其他城市和地区。 (2)相似性大小与短时客流可预测性强度相关。研究发现工作日比双休日短时客流可预测性强,高峰比平峰的短时OD客流可预测性强,早高峰比晚高峰的短时OD客流可预测性强。对于本文案例,进行车站短时进站量预测时,要满足全网90%车站0.9的预测精度最小时间粒度应取8 min;预测高峰时段短时OD客流时,要满足全网90%车站0.9的预测精度最小时间粒度应为60 min。 (3)工作日车站可预测等级变化较小,双休日车站可预测等级普遍较低;结合不同等级车站空间分布特征发现,周边用地性质单一的车站可预测等级较高,用地混合程度高的车站可预测等级较低。 准确掌握较精细时间粒度的客流规律对城市轨道交通网络化运营客流监测、优化运营方案、保证运输安全等具有重要意义。研究车站层级的短时客流规律对预测方法改进具有指导作用,适合不同时间段、不同等级车站的短时客流预测方法将是进一步研究的方向。 参考文献: [1]姚恩建, 程欣, 刘莎莎, 等. 基于可达性的城轨既有站进出站客流预测[J]. 铁道学报, 2016,38(1):1-7. YAO Enjian, CHENG Xin, LIU Shasha, et al. Accessibility-based Forecast on Passenger Flow Entering and Departing Existing Urban Railway Stations [J].Journal of the China Railway Society, 2016,38(1):1-7. [2]四兵锋, 何九冉, 任华玲,等. 基于时序特征的城市轨道交通客流预测[J]. 北京交通大学学报, 2014, 38(3):1-6. SI Bingfeng, HE Jiuran, REN Hualing, et al. Urban Railway Traffic Passenger Flow Forecast Based on the Timing Characteristics [J]. Journal of Beijing Jiaotong University, 2014, 38(3):1-6. [3]邹东, 刘琼, 黄梓荣. 城市轨道交通线网时空相关性客流预测研究[J]. 城市轨道交通研究, 2016, 19(3):32-37. ZOU Dong, LIU Qiong, HUANG Zirong. Spatial-temporal Correlation Prediction for Passenger Flow in Urban Rail Transit Network [J]. Urban Mass Transit, 2016, 19(3):32-37. [4] 刘美琪, 焦朋朋, 孙拓. 城市轨道交通进站客流量短时预测模型研究[J]. 城市轨道交通研究, 2015,18(11):13-17, 29. LIU Meiqi, JIAO Pengpeng, SUN Tuo. On Short-term Forecasting Model of Passenger Flow in Urban Rail Transit [J]. Urban Mass Transit, 2015,18(11):13-17, 29. [5] 周玮腾, 韩宝明, 李得伟,等. 城市轨道交通客流分布短时预测模型研究及应用[J]. 城市轨道交通研究, 2015, 18(2):24-28. ZHOU Weiteng, HAN Baoming, LI Dewei, et al. Research and Application of Short-term Forecast Model on Passenger Flow Distribution in Urban Mass Transit [J]. Urban Mass Transit, 2015, 18(2):24-28. [6]姚向明, 赵鹏, 禹丹丹. 城市轨道交通网络短时客流OD估计模型[J]. 交通运输系统工程与信息, 2015, 15(2):149-155. YAO Xiangming, ZHAO Peng, YU Dandan. Short-time Passenger Flow Origin-destination Estimation Model for Urban Rail Transit Network [J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(2):149-155. [7]杜豫川, 孙轶凡, 陈赣浙. 快速路网实时OD预测的时间颗粒度选择[J]. 同济大学学报:自然科学版, 2016, 44(10):1553-1558. DU Yuchuan, SUN Yifan, CHEN Ganzhe. Time Granularity Selection for Expressway OD Real-time Prediction [J]. Journal of Tongji University:Natural Science, 2016, 44(10):1553-1558. [8]CHENZHONG M B. Variability in Regularity: Mining Temporal Mobility Patterns in London, Singapore and Beijing Using Smart-card Data[J]. Plos One, 2016,2(11):1-17. [9]乐逸祥, 周磊山, 齐向春. 基于分形插值方法的城市轨道交通车站客流拟合与仿真[J]. 铁道学报, 2012, 34(8):7-12. YUE Yixiang, ZHOU Leishan, QI Xiangchun. Using Fractal Interpolation Model to Simulate Passenger Flow Sequence in Urban Rail Transit Station [J]. Journal of the China Railway Society, 2012, 34(8):7-12. [10]夏学文, 谢世浩. 用时序分析法建立轨道谱[J]. 铁道学报, 1991,13(3):67-76. XIA Xuewen, XIE Shihao. Setting up Railway Track Spectra by the Method of Time Series Analysis [J]. Journal of the China Railway Society, 1991,13(3):67-76. [11]韩晋, 杨岳, 陈峰, 等. 基于非等时距加权灰色模型与神经网络的轨道不平顺预测[J]. 铁道学报, 2014, 36(1):81-87. HAN Jin, YANG Yue, CHEN Feng, et al. Prediction of Track Irregularity Based on Non-equal Interval Weighted Grey Model and Neural Network [J]. Journal of the China Railway Society, 2014, 36(1):81-87. [12]KEOGH E, KASETTY S. On the Need for Time Series Data Mining Benchmarks: a Survey and Empirical Demonstration[J]. Data Mining and Knowledge Discovery, 2003,7(4):349-371. [13]姜婷婷, 肖卫东, 张翀,等. 基于桑基图的时间序列文本可视化方法[J]. 计算机应用研究, 2016, 33(9):2683-2687. JIANG Tingting, XIAO Weidong, ZHANG Chong, et al. Text Visualization Method for Time Series Based on Sankey Diagram [J]. Application Research of Computers, 2016, 33(9):2683-2687. [14]刘强, 贾利民. 基于复杂系统的铁路客流影响因素分析研究[J]. 铁道运输与经济, 2008, 30(11):14-19. LIU Qiang, JIA Limin. Study on Factors Influencing Railway Passenger Flow under Complex System [J]. Railway Transport and Economy, 2008, 30(11):14-19. [15]王波. 上海轨道交通早高峰客流拥挤与居民通勤关系分析[J]. 城市轨道交通研究, 2016, 19(7):75-78. WANG Bo. Relationship between the Rush Hour Passenger Flow Congestion and Residents Commuting in Shanghai Rail Transit System [J]. Urban Mass Transit, 2016, 19(7):75-78. [16]李俊芳, 姚敏峰, 季峰,等. 土地利用混合度对轨道交通车站客流的影响[J]. 同济大学学报:自然科学版, 2016, 44(9):1415-1423. LI Junfang, YAO Minfeng, JI Feng, et al. Quantitative Study on How Land Use Mix Impact Urban Rail Transit at Station-level [J]. Journal of Tongji University:Natural Science, 2016, 44(9):1415-1423.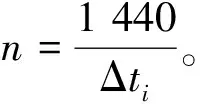

1.3 相似性度量方法
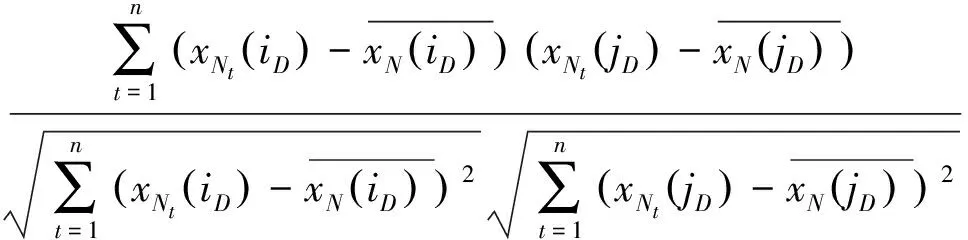
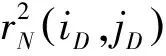
2 北京地铁出行规律相似性度量
2.1 车站进站客流相似性
2.2 车站OD客流相似性





3 可预测性等级划分
3.1 不同等级车站时间分布
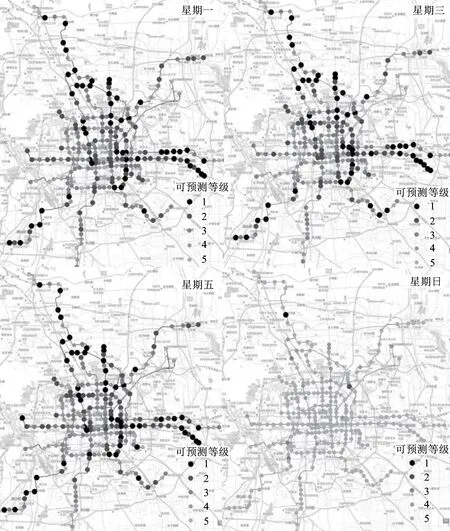
3.2 不同等级车站空间分布
4 结论
