设有挡肩的尾端圆弧接触重载车钩稳钩能力研究

钟文生, 汪 煌，张江田, 姚 远,3

(1.西南交通大学 牵引动力国家重点实验室， 四川 成都 610031；2.北车集团大同电力机车有限责任公司 技术中心，山西 大同 037038；3.大功率交流传动电力机车系统集成国家重点实验室，湖南 株洲 412001)

近年来，重载列车制动时牵引机车车钩失稳问题得到了国内外的广泛关注[1-8]。列车制动产生的车钩横向分力形成倾覆力矩导致车钩横向失稳。除了合理的机车二系悬挂参数匹配以外[9]，还需要合理的车钩结构设计以提高车钩的稳钩能力。目前国内重载机车车钩按稳钩原理大致分为两类：第一类利用车钩尾端摩擦圆弧接触，通过机构运动实现较小的车钩横向分力，如101车钩；第二类是通过设置止挡，限止车钩发生大转角，从而保持车钩的稳定，如LAF车钩和102车钩。两类车钩分别采用扁销和圆销以实现钩体与钩尾框的连接。两类车钩有各自的优缺点，止挡车钩能限止车钩最大转角，但在常用状态车钩转角较小时形成较大的横向分力，导致机车轮轴横向力较大；尾端摩擦圆弧接触车钩在小角度具有小横向分力，但一旦失稳车钩转角较大，形成较大的车钩分力。

本文针对尾端摩擦圆弧接触车钩，通过改进尾端圆弧形状，在两侧增加挡肩结构，通过挡肩的止挡作用减小车钩转角。从车钩的运动状态和受力的角度分析车钩的稳钩原理，并通过动力学计算仿真，研究车钩稳钩能力及其与机车二系悬挂参数的匹配规律。

1 挡肩圆弧车钩的结构及特点

1.1 车钩结构说明

我国内燃电力机车车钩(101号车钩)如图1所示，采用车钩尾端摩擦圆弧接触，车钩与钩尾框通过钩尾销连接，车钩尾端与前从板之间通过圆弧接触。前从板与车钩尾端面接触两圆弧半径R和r分别为150 mm和130 mm，即摩擦圆弧接触面为线接触。当车钩体相对前从板偏转时，圆弧面接触点沿着圆弧运动，在摩擦力达到饱和之前，两圆弧面之间为滚动，而不是纯滑动。根据文献[3]研究，圆弧接触位置沿圆弧横向移动，以实现车钩传力线转角小于车钩体实际偏转角，即减小车钩横向分力，该车钩在小角度下表现出较好的稳钩能力，且机车轮轴横向力小。但是该车钩没有设置止挡，一旦发生车钩受压失稳，较大的车钩角度使得机车轮轴横向力超标甚至导致列车安全运行事故。

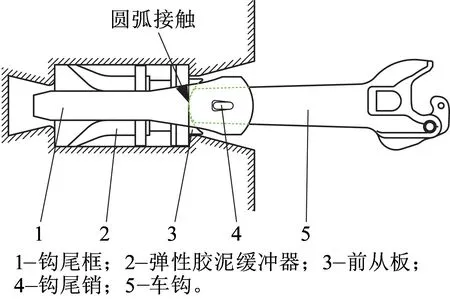
图1 尾端圆弧接触车钩示意图

本文在该尾端圆弧接触车钩结构的基础上，在车钩尾端增加挡肩止挡结构。一旦车钩转角超过一定角度时，车钩一侧凸起挡肩与从板止挡接触，阻止车钩转角进一步增大，提高车钩稳钩能力。

1.2 车钩运动状态与受力分析

车钩尾端圆弧与止挡受力分析如图2所示，当车钩转角α超过一定角度时，车钩一侧挡肩与从板止挡接触。由车钩尾端与从板圆弧接触副作用，圆弧接触点沿弧面运动，传递车钩纵向力。此时车钩尾端为两点接触状态，车钩运动状态与受力分析如图3所示。车钩两端圆弧接触点连线仍为车钩传力线，传递车钩部分纵向力，该传力线为两端摩擦圆的内公切线，若圆弧接触面摩擦达到饱和，传力线与轨道夹角θ大于0时，圆弧接触点位置会沿着圆弧面反向回滑，此时，传力线与轨道夹角大于0，即车钩产生横向分力。通过机车二系悬挂横向运动的回复力和车钩尾端止挡力平衡该倾覆力矩，若机车二系横向刚度过小或止挡间隙过大，车钩转角会增大，有可能使得车钩失稳。

图2 车钩尾端圆弧接触运动与受力分析

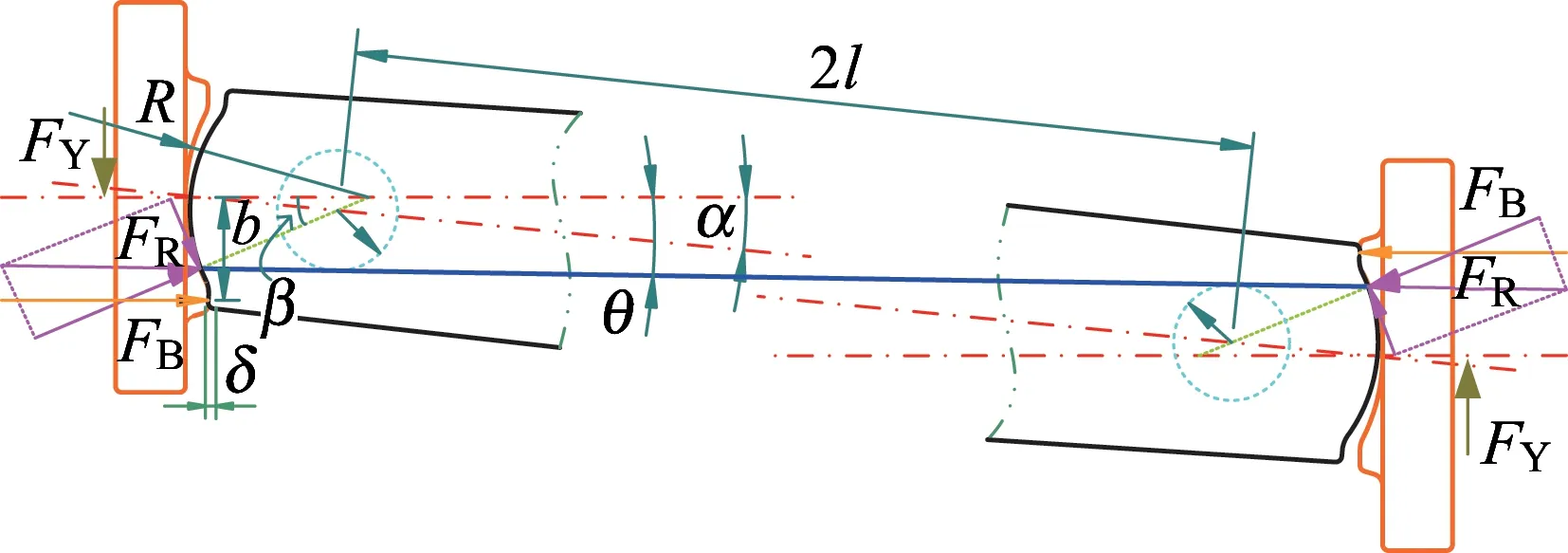
图3 车钩运动状态与受力分析

根据车钩转角与止挡间隙大小的关系，可将车钩运动分为如下4个过程，进行稳态受力分析。

(1) 车钩转角较小时，相邻车体的横向相对位移小于车体横向临界相对位移2Ybc，接触点沿着圆弧面滚动，车钩无横向力，其中Ybc和车钩临界转角αc可以表示为[3]

Ybc=R·sin(arctanμ)

( 1 )

( 2 )

圆弧车钩产生横向力对应车体临界横向相对位移2Ybc和车钩转角αc与圆弧面摩擦系数的关系如图4所示。可见，在车钩转角较小的情况下，圆弧面摩擦系数越大，圆弧车钩产生横向力对应的车体横向临界相对位移和车钩临界转角越大。

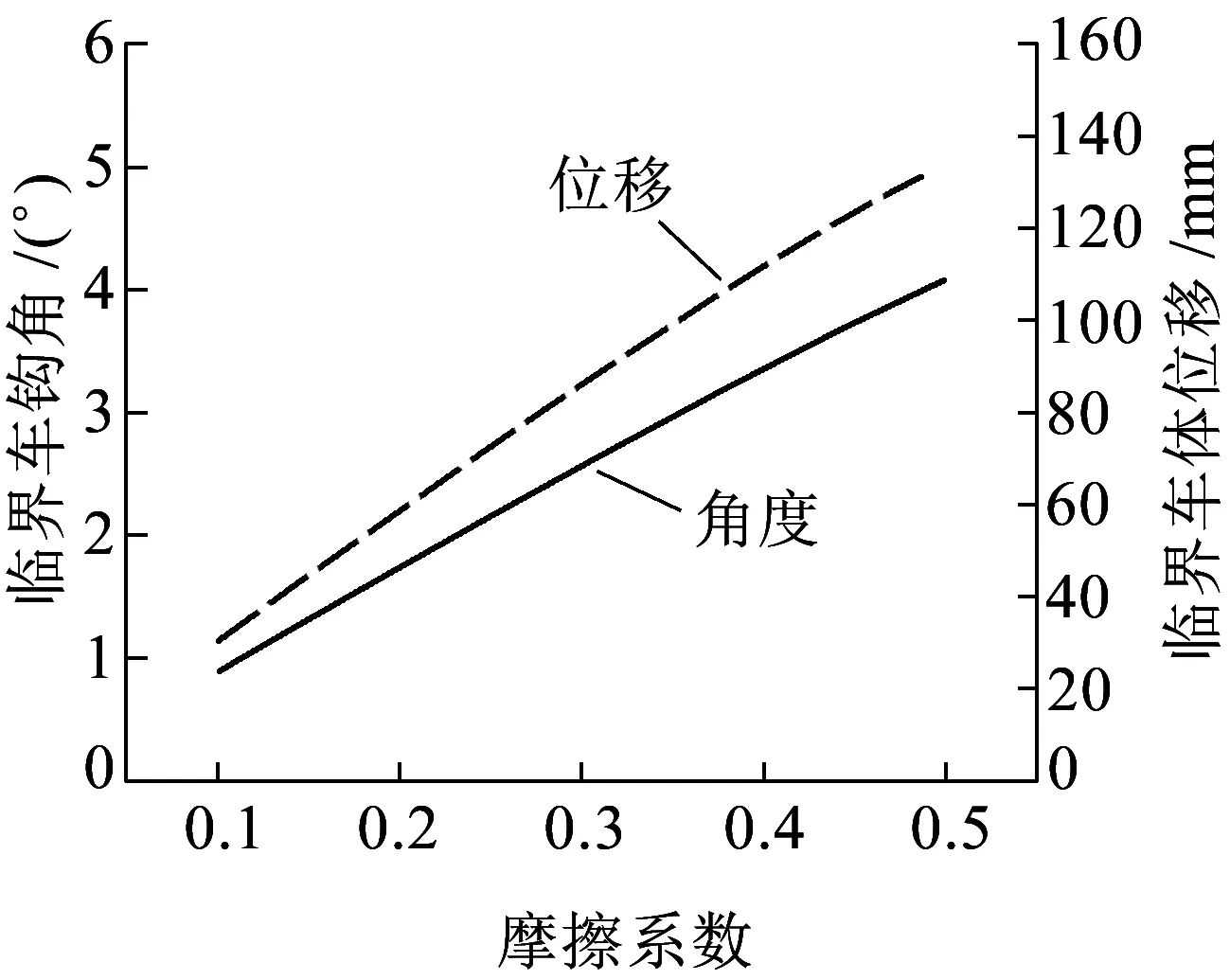
图4 车钩产生横向分力对应车体位移和车钩转角

(2) 车钩转角较大时，圆弧接触面摩擦达到饱和，接触点位置沿圆弧面反向滑动，传力线为车钩两端摩擦圆的内公切线。该过程假设止挡纵向间隙较大，未发生止挡接触，即要求止挡间隙δ满足式( 3 )要求。

δ>b·sinαc

( 3 )

式中：b为车钩中心到止挡的横向距离，文中假设为75 mm。

该条件下，车钩横向力Fcy和传力线转角θ为

Fcy=Fc·sinθ

( 4 )

( 5 )

车钩上作用的力矩，即导致车钩倾覆的失稳力矩Tc为

Tc=Fccosθ·2lsinθ

( 6 )

式中：Fc为车钩受压的纵向力。

图5为机车悬挂对稳定车钩的原理示意图，机车悬挂提供横向回复作用力平衡车钩横向分力。忽略机车一系悬挂的影响，机车横向悬挂回复力对车钩的平衡力矩Ts为

( 7 )

图5 机车悬挂对车钩的稳定原理

当Ts=Tc时，为车钩临界稳定状态，由此计算车钩的承载能力为

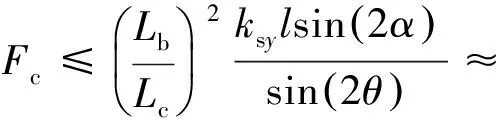
( 8 )

不同车钩纵向力作用下车钩稳定转角为

( 9 )

图6为静态下不同结构参数对应的车钩临界失稳转角，图6中曲线左下方为稳定区域。可见，车钩失稳临界转角主要取决于尾端圆弧面摩擦系数，增加圆弧面摩擦系数有利于提高车钩稳钩能力；车钩纵向力和机车二系横向刚度对车钩临界失稳转角也有比较明显的影响，随着车钩纵向力的增大，车钩临界失稳转角减小；车钩受压纵向力越小，增加机车二系横向刚度对提高车钩失稳临界转角越明显。当车钩钩尾圆弧面接触面摩擦系数为0.2、0.3和0.4时，车钩转角的临界失稳转角分别为2.2°、3.3°和4.2°。

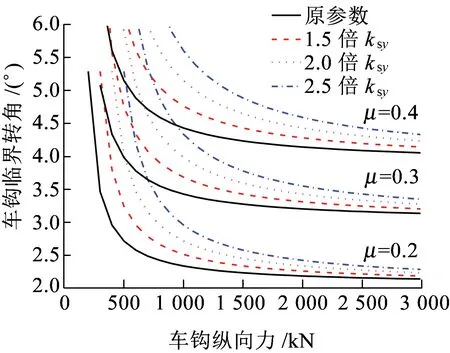
图6 不同结构参数对应的车钩临界转角

(3) 圆弧接触面摩擦达到饱和，且发生止挡接触，止挡传递纵向力，起到稳钩的作用。车钩转角与止挡间隙δ满足式(10)要求。

(10)

建立力平衡方程

FRcosθ+FB=Fc

(11)

(12)

FRcosθ·2lsinθ-FY·2lcosα-2FB(b-R·sin(arctan(μ-θ)))=0

(13)

式中：FR和FB分别为圆弧和止挡传递的纵向力。

由于实际车钩失稳为车钩转角突然增大的过程，会造成止挡接触冲击力，根据仿真结果，稳态公式计算考虑到一倍的止挡纵向动载荷。不同的圆弧摩擦系数和机车二系悬挂单弹簧横向刚度计算的FB/Fc结果如图7和图8所示。可见，增加圆弧面摩擦系数及机车二系横向悬挂刚度，可减小车钩挡肩止挡作用力；车钩压缩力及挡肩止挡间隙越大，车钩挡肩止挡作用力越大。当FB/Fc大于等于1时，车钩与从板圆弧面脱离，车钩易失稳。

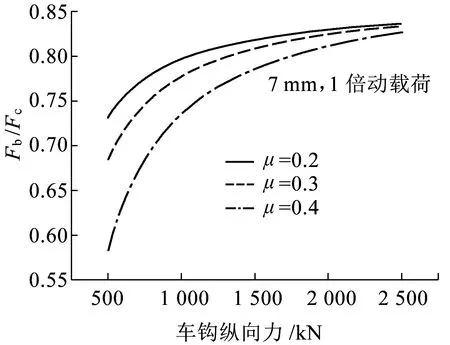
图7 不同圆弧面摩擦系数对应挡肩作用力

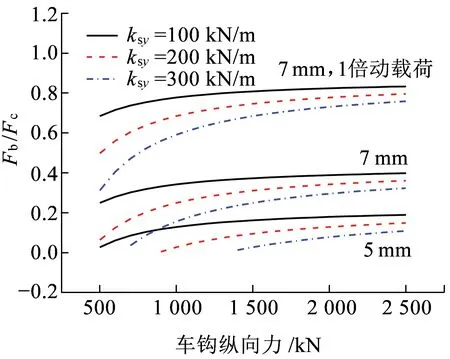
图8 不同机车二系悬挂刚度对应挡肩作用力

(4) 车钩与从板圆弧面脱离，车钩尾端为止挡单点接触。车钩转角与止挡间隙δ满足式(14)要求。

(14)

车钩两端止挡连线为车钩实际传力线，其转角θ与车钩转角α的关系如式(15)所示，结合式( 6 )和式( 7 )，可得稳态条件下车钩稳定临界转角为

(15)

(16)

图9为不同的车钩纵向压缩力和机车二系单个弹簧横向刚度对应车钩失稳的临界转角。可见，车钩尾端止挡接触时，车钩纵向压缩力越大，车钩临界稳定转角越小；增大机车二系横向刚度，可以提高车钩临界稳定转角，车钩纵向力越小，机车二系横向刚度对提高该临界稳定转角的效果越明显。

2 机车动力学与车钩稳定性

利用SIMPACK软件建立采用两个车钩连接的三节机车多体动力学模型，具体的机车结构动力学参数及计算工况见参考文献[3]。在此模型基础上，增加车钩尾端挡肩止挡作用，挡肩止挡通过单边力模拟，挡肩止挡横向跨距为150 mm。不同车钩纵向压缩力、圆弧摩擦系数、机车二系横向刚度和车钩止挡纵向间隙对应的机车轮轴横向力如图10～图12所示。

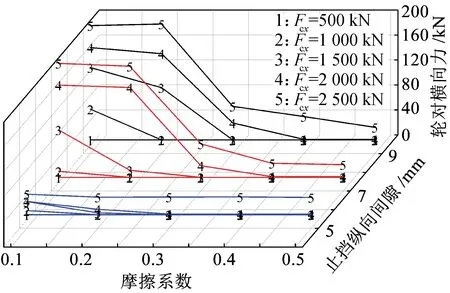
图10 二系簧横向刚度为100 kN/m对应计算结果

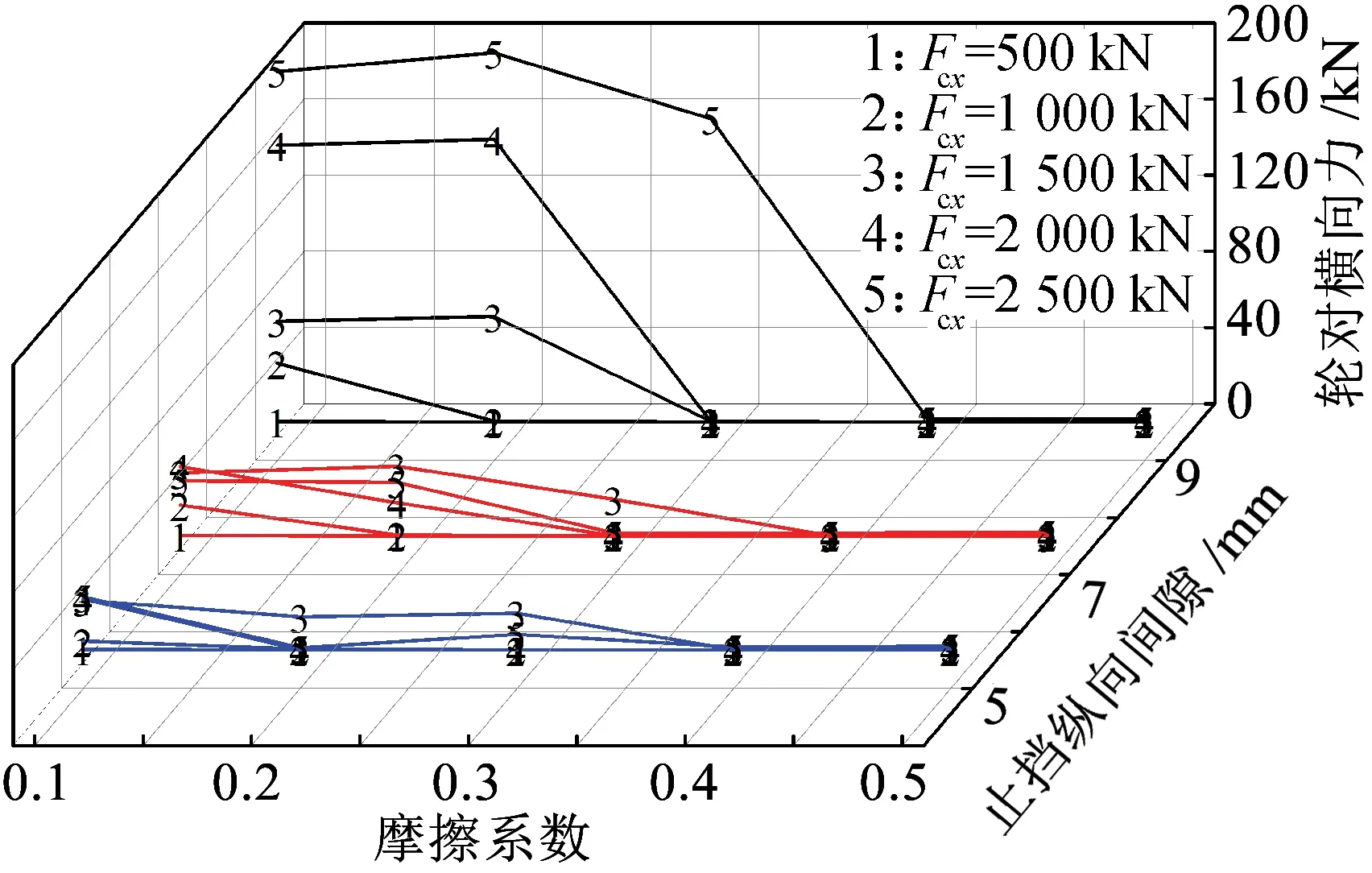
图11 二系簧横向刚度为200 kN/m对应计算结果

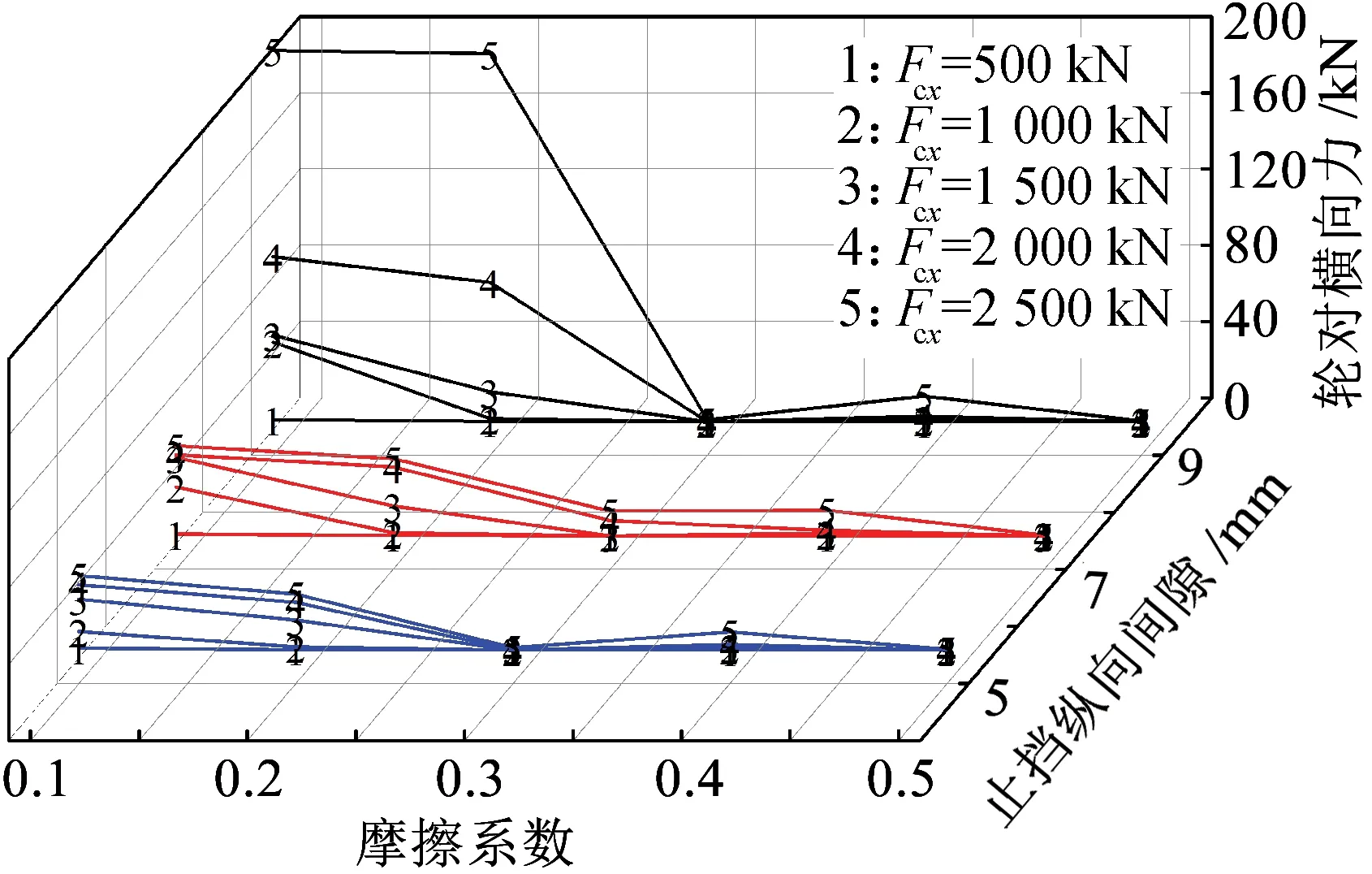
图12 二系簧横向刚度为300 kN/m对应计算结果

图10为机车单个二系簧横向刚度为100 kN/m时对应的计算结果。水平面坐标分别为圆弧面摩擦系数和止挡纵向间隙，垂向坐标为计算轮轴横向力。当止挡纵向间隙为5 mm，车钩力为2 500 kN以及摩擦系数为0.1情况下，车钩保持稳定，止挡作用下明显提高车钩稳定性；而止挡纵向间隙为7 mm，车钩力为2 000 kN以及摩擦系数小于0.3时，车钩失稳；止挡纵向间隙为9 mm，车钩力为1 500 kN以及摩擦系数小于0.3时，车钩失稳。

图11为机车单个二系簧横向刚度为200 kN/m时对应的计算结果。止挡纵向间隙为7 mm，车钩力为2 500 kN以及摩擦系数为0.1情况下，车钩保持稳定；止挡纵向间隙为9 mm，车钩力为2 000 kN以及摩擦系数小于0.3时，车钩失稳。

图12为机车单个二系簧横向刚度为300 kN/m时对应的计算结果。止挡纵向间隙为7 mm，车钩力为2 500 kN以及摩擦系数为0.1情况下，车钩保持稳定；止挡纵向间隙为9 mm，车钩力为2 500 kN以及摩擦系数小于0.3时，车钩失稳。

可见，较小的二系横向止挡间隙及较大的机车二系横向刚度有利于提高该类车钩的稳钩能力。止挡间隙值较大时，由于车钩失稳的冲击作用，即使止挡接触，也并不能保证较大纵向压缩力作用下的车钩稳定性。

3 结论

(1) 设置并保证较小止挡间隙，以及增加机车二系横向刚度可明显提高较大压缩载荷作用下尾端圆弧加止挡车钩的稳定性。

(2) 止挡间隙值较大时，由于车钩失稳的冲击作用，即使止挡接触，也并不能保证较大纵向压缩力作用下的车钩稳定性。

(3) 挡肩止挡间隙为5 mm、机车二系横向刚度为100 kN/m时，车钩满足最大纵向载荷为2 500 kN计算工况稳定性的要求；当止挡间隙为7 mm时，机车二系簧横向刚度需提高一倍才满足该纵向载荷作用下车钩稳定要求。

参考文献：

[1]DURALI M, SHADMEHRI B. Nonlinear Analysis of Train Derailment in Severe Braking[J]. Journal of Dynamic Systems Measurement & Control, 2003,125 (1): 48-53.

[2]MA W H, LUO S H, SONG R R. Coupler Dynamic Performance Analysis of Heavy Haul Locomotive[J]. Vehicle System Dynamics, 2012, 50(9):1435-1452.

[3]YAO Y, ZHANG X X, ZHANG H J. The Stability Mechanism and Its Application of Heavy Haul Couplers with Arc Surface Contact[J]. Vehicle System Dynamics, 2013, 51(9):1324-1341.

[4]WU Q, LUO S H, XU Z Q. Coupler Jackknifing and Derailments of Locomotives on Tangent Track[J]. Vehicle System Dynamics, 2013, 51(11):1784-1800.

[5]XU Z Q, MA W H, WU Q. Coupler Rotation Behaviour and Its Effect on Heavy Haul Trains [J]. Vehicle System Dynamics, 2013, 51(11)：1523-1538.

[6]YAO Y, LIU X, ZHANG H J. The Stability and Mechanical Characteristics of Heavy Haul Couplers with Restoring Bumpstop[J]. Vehicle System Dynamics， 2014,52(1):26-44.

[7]YAO Y, ZHANG X X, ZHANG H J. Dynamic Performances of an Innovative Coupler Used in Heavy Haul Trains [J]. Vehicle System Dynamics, 2014,52(10):1288-1303.

[8]WU G S, WANG H, YAO Y. Improvements for the Stability of Heavy Haul Couplers with Arc Surface Contact[J]. Vehicle System Dynamics, 2018,56(3):428-442.

[9]姚远，杨俊杰，张红军. 重载车钩选型与机车悬挂参数匹配研究[C]// 铁路重载运输技术交流会论文集. 北京：中国铁道出版社,2014.