配合间隙对溢流阀稳态液动力的影响

瞿道海 周云山 罗 威 刘云峰 傅 兵

湖南大学机械与运载工程学院，长沙，410082

0 引言

溢流阀广泛用于液压系统中，经常与先导电磁阀或电磁铁配合使用，控制液压系统的压力在一定范围内变化[1-4]。当需要液压系统的压力精确跟随控制信号变化时，液动力成了关键影响因素。国内外许多学者对液动力进行了深入研究。冀宏等[5]利用流场动力学方法，对非全周开口U形和V形节流槽滑阀流场进行可视化研究，发现在特定的阀口开度范围内，液动力会使阀口趋于开大；吴小锋等[6]通过计算流体动力学方法对液压换向阀受到的瞬态液动力进行研究，以减小噪声因子对瞬态液动力的影响，提高换向阀的健壮性；YUAN等[7]、KRISHNASWAMY等[8]对大流量多位电液换向阀的液动力进行研究，通过理论、CFD仿真和试验相结合的方法，利用液动力来提高电液换向阀的灵敏性。少数学者对配合间隙进行了研究。刘晓红等[9]建立了具有配合间隙的阀芯CFD模型，仿真与试验结果表明，流体在滑阀节流口的能量损失会使油温升高、阀芯膨胀，阀芯与阀体之间的配合间隙减小，最终导致阀芯卡滞；PAN等[10]研究了电液伺服阀径向配合间隙对节流边流量特性的影响；WEI等[11]在考虑减小泄漏量和避免阀芯卡滞的情况下，研究了大直径滑阀与阀体之间的配合间隙应如何设计。综上，学者们都未考虑阀芯与阀体间配合间隙对滑阀液动力的影响。

本文以汽车某自动变速器先导式电液比例溢流阀为研究对象，建立了内流式滑阀液动力数学模型，将滑阀与阀体配合间隙考虑在内，基于CFD仿真平台构建了流体域模型，搭建试验测试平台，验证考虑配合间隙的仿真模型的合理性；最后，基于验证的仿真模型，分析不同配合间隙对滑阀稳态液动力的影响。

1 液动力对溢流阀的影响

流体在滑阀阀腔流动时，造成阀腔环形侧面压力分布发生变化，产生作用于滑阀的作用力即液动力[12]。液动力分为瞬态液动力和稳态液动力。液体加速或减速引起的作用于滑阀环形侧面的作用力称为瞬态液动力；流出和流入控制体的速度发生变化，产生作用于滑阀环形侧面的作用力称为稳态液动力。

某先导式电液比例溢流阀由滑阀、弹簧、比例电磁阀和阀体等组成，结构如图1所示。溢流滑阀的动力学平衡方程为[13]

Fa=Fpilot-Ffeedback+Ff-Ffriction+Fspring

(1)

式中，Fa为滑阀受到的惯性力；Fpilot为先导力；Ffeedback为反馈力；Ff为液动力；Ffriction为摩擦力；Fspring为弹簧力。

可以看出，液动力影响滑阀的力学平衡关系。

图1 溢流阀结构简图Fig.1 Structure diagram of relief valve

图2所示为某国产无级变速器液压系统电液比例溢流阀在不同初始溢流压力p0下，溢流流量增加时的溢流压力的变化。可以看出，溢流压力呈明显增大趋势，这是由于溢流流量增大时，流体作用于滑阀的液动力增大，改变了滑阀的力学平衡关系，这对变速器的夹紧力控制和速比跟踪等都是非常不利的。

图2 液动力对溢流阀的影响Fig.2 Influence of steady-state fluid force to relief valve

2 液动力模型

溢流阀的液动力产生于节流口和泄油口之间，将该区域提取出来，如图3所示，其中，Δx为滑阀节流边阀口的开度，δ为滑阀与阀体之间的配合间隙，θ1为流体从节流口射入阀腔的射流角度，θ2为流体从滑阀流出的射流角度，v1、v2分别为流体射入阀腔和流出阀腔的平均速度，qV1、qV2分别为流体流入阀腔和流出阀腔的流量，p1、p2分别为流体流入阀腔和流出阀腔的压力，d为阀芯外径，D为阀体内径，τsleeve为阀体作用在流体上的黏性剪切应力，τrod为流体施加在阀杆上的黏性剪切应力。

图3 内流式滑阀节流区域Fig.3 Throttling area of converged flow spool

以滑阀为研究对象，当流体流经滑阀滑槽表面时，施加于滑阀的作用力Fspool由三部分组成：①流体具有黏性，贴近滑阀表面油液速度为0，产生了施加于滑阀的黏性摩擦力Frod；②油液流经滑槽时速度变化剧烈，有动压产生，产生作用于滑阀环形侧面的作用力Fdynamics；③流体静压产生作用于滑阀环形侧面的作用力Fstatics。Fspool的计算公式为

Fspool=Frod+Fdynamics+Fstatics=
∬Ar(prs+prd)dA-∬Al(pls+pld)dA+∬ArodτroddA

(2)

式中，prs、pls分别为作用于滑阀右边和左边台肩面的静压力；prd、pld分别为作用于滑阀右边和左边台肩面的动压力；Ar、Al分别为滑阀右边和左边环形侧面面积；Arod为阀杆表面积。

以控制流体为研究对象，作用于控制流体的作用力Ffluid由两部分组成：①滑阀施加于流体的反作用力-Fspool；②流体具有黏性，贴近阀体表面的油液速度为0，流体产生了施加于阀体的黏性摩擦力Fsleeve，则阀体对流体施加了反作用力-Fsleeve。Ffluid的计算公式为

Ffluid=(-Fspool)+(-Fsleeve)=
-Fspool-∬AsleeveτsleevedA

(3)

式中，Asleeve为阀体与控制流体接触的表面积。

由动量守恒定理可得

(4)

式中，V为控制流体体积；ρ为流体密度；v、vx分别为流体速度和它沿阀芯轴向的分量；n为对应于微分dA向外的法向单位矢量。

式(4)等号右边第一项为滑阀受到的瞬态液动力，第二项为流体流入阀腔和流出阀腔动量变化引起的稳态液动力，且

∬Aρvxv·ndA=∬Ainletρvxv·idA+
∬Aoutletρvxv·(-i)dA

(5)

式中，Ainlet、Aoutlet分别为流体流入滑阀和流出滑阀的过流面积；i为沿滑阀轴向、方向向右的单位法向量(图3)。

为了突出本文研究重点，做出以下假设：①流体流经滑阀过程中，体积流量不变；②流体为定常流动，忽略瞬态液动力影响；③本文研究的滑阀通流流量和油液黏度均较小，阀体施加于流体的作用力忽略不计[7]；④出口流体流速相对入口较小，且射流角很大，忽略出口动量对稳态液动力的影响；⑤假设流体流入阀口的速度都可用v1表示。

联立式(3)～式(5)可得滑阀受到的液动力：

Fspool≈∬Ainletρvxv·idA=ρv1qV1cosθ1

(6)

(7)

(8)

式中，Cq为流量系数；A(x)为流体流经滑阀节流边的过流面积；Δp为节流口前后的压差。

滑阀与阀体之间存在配合间隙，流体流入节流口的过流面积为锥面，可表示为

(9)

将式(7)～式(9)代入式(6)，得

(10)

3 流场可视化分析及试验验证

由于机械加工精度、滑阀质量、安装误差以及油液含有杂质颗粒等原因，为保证滑阀在阀体内部顺畅移动而不会出现卡滞，滑阀与阀体之间会设计配合间隙，同时为了减小滑阀与阀体之间的泄漏量，设计的配合间隙应控制在合理范围内，液压元件中相对运动的零件之间的间隙一般在几微米到几十微米之间[14]。本文选取配合间隙为20 μm的滑阀和阀体作为试验对象，对配合间隙为0和20 μm的滑阀仿真结果与试验测试数据进行对比，以验证考虑配合间隙仿真模型的合理性。

3.1 网格划分及独立性验证

本文采用滑移网格计算方法，用ICEM CFD软件划分网格，然后将划分的网格导入Fluent分析软件进行计算。将滑阀计算域分为四部分：入口域、配合间隙域、运动域和出口域，如图4所示。入口域设为速度入口，根据入口流量转换为不同速度值；配合间隙域代表滑阀与阀体之间的配合间隙；运动域代表流经阀腔的流体，沿节流口由关闭到打开方向轴向移动，速度设置为2 μm/s；出口域为压力出口，压力设定为0.1 MPa。滑阀、阀体和其余主要边界条件参数见表1。

(a)滑阀计算域模型 (b)配合间隙模型图4 滑阀计算域网格Fig.4 Computational meshes of spool

参数数值油液密度ρ(kg/m3)847.7动力黏度μ(Pa·s)0.05阀芯外径d(mm)13.978阀芯反馈直径d0(mm)13.060阀杆直径drod(mm)6.500阀体内径D(mm)14.018弹簧刚度k(N/mm)0.973弹簧预紧长度x0(mm)20.51

几何模型忽略阀体沉割槽圆角的影响，由于结构简单，结构化网格具有质量高、占用内存较少等优点，因此，采用结构化网格对几何模型进行划分。本文的研究对象是稳态液动力，影响稳态液动力的区域主要分布在流体流进滑阀节流边附近，由于节流边处压力和速度梯度变化很大，故存在涡流等复杂流态[12]。对节流口附近的入口域、配合间隙域和运动域进行网格加密处理，如图4所示，其他区域压力变化不大，采用粗网格处理。

为了保证仿真结果不受网格数量影响，并缩短计算时间，网格层数需通过网格独立性验证确定。以配合间隙域层数确定为例，如图5所示，在相同边界条件下，当配合间隙域加密部分网格层数达到200时，入口压力基本维持不变，即以该层数作为配合间隙域的加密层数。最终，计算域网格总数确定在140万左右。

图5 网格独立性验证Fig.5 Mesh independence verified

(a)压力云图 (b)速度矢量图图6 δ=0的仿真结果Fig.6 Simulation results of δ=0

(a)压力云图 (b)速度矢量图图7 δ=20 μm的仿真结果Fig.6 Simulation results of δ=20 μm

3.2 压力场与速度场分析

图6、图7分别为配合间隙为0和20 μm，入口流量为12 L/min、入口计算压力为3 MPa时的压力云图与速度矢量图。可以看出，在相同的入口压力和输入流量下，当配合间隙为0时，流体在流经节流口时基本贴近阀芯壁面，当配合间隙为20 μm时流体流经节流口的射流角明显要小于配合间隙为0时的射流角，速度大于配合间隙为0时的速度。

3.3 试验验证

搭建的试验测试平台如图8所示，测试台液压回路如图9所示。流量计选用抗电磁干扰型电子式数显涡轮式流量计，测试范围为3～20 L/min，测量精度1%；压力传感器测量范围为0～6 MPa，测量精度0.5%，油泵为双作用叶片泵，单泵排量7.5 mL/r，电机转速范围0～2 400 r/min。

图8 试验测试台Fig.8 Test rig

1.电机 2.双作用叶片泵 3.流量计 4.待测溢流阀5，7.压力传感器 6.比例电磁阀 8.定值溢流阀图9 测试台液压回路Fig.9 Hydraulic circuit of test rig

将比例电磁阀控制电流由0线性变化至1 A，其中，控制电流变化间隔为0.001 A，驱动频率为50 Hz。用压力传感器5、7分别测得滑阀受到的先导压力pp和溢流压力p1；驱动电流变化较慢，可以认为滑阀一直在稳态，即忽略瞬态液动力、摩擦力以及惯性力的影响；溢流阀工作时，工作位置基本在节流边附近。弹簧刚度比较小，可认为弹簧一直保持在预紧力位置。由式(1)可得

(11)

对比通流流量在12 L/min和18 L/min时稳态液动力与溢流压力关系，如图10、图11所示。可以看出，在不同通流流量下，考虑配合间隙的仿真结果在趋势和数值上与试验测试结果吻合，随着压力的升高，液动力基本呈线性增加；而未考虑配合间隙的仿真结果无论在趋势还是数值上，与实测数据相差都很大，基本不随压力的升高而变化。因此，考虑配合间隙的滑阀计算域模型可以用来研究流体在滑阀节流口的流动特性，能真实反映出滑阀受到的液动力情况。

图10 qV1=12 L/min的对比结果Fig.10 Comparison result of qV1=12 L/min

图11 qV1=18 L/min的对比结果Fig.11 Comparison result of qV1=18 L/min

4 配合间隙对稳态液动力的影响

由式(10)可以看出，阀口开度Δx、入口射流角度θ、配合间隙δ和压差Δp会影响稳态液动力大小，将仿真模型输入流量定为6 L/min，在配合间隙分别为0、10 μm、20 μm、30 μm和40 μm时，研究它们之间的变化关系。

4.1 配合间隙对溢流阀阀口开度的影响

图12所示为不同的配合间隙下，滑阀开度与溢流阀工作压力的关系。可以看出，在溢流阀压力变化过程中，阀口开度都维持在微米数量级，与配合间隙非常接近；在相同工作压力下，随着配合间隙的增大，阀芯开度越来越小，当间隙超过某临界值后，溢流阀最大工作压力将受到限制；在同一配合间隙下，随着工作压力升高，阀口开度越来越小，并且阀口开度对溢流压力的变化斜率也越来越小，即随着压力升高，溢流压力对阀口开度的变化越来越敏感。

图12 阀口开度与溢流压力的关系Fig.12 Relationship between valve opening and relief pressure

4.2 配合间隙对入口射流角的影响

射流角度计算方法[15]：将滑阀节流边开口对应的配合间隙区域均匀等分成n个矩形，每个矩形对应轴向速度ui和径向速度vi，沿轴向的长度为dx，沿径向的长度为dy，则射流角为

(12)

图13所示为不同配合间隙下，射流角与滑阀开度的关系。可以看出，有无配合间隙时，滑阀射流角随滑阀开度变化的趋势明显不同。没有配合间隙时，滑阀在打开过程中，射流角由90°缓慢降低并稳定至70°附近。存在配合间隙时，随着阀口开度增大，射流角由20°附近逐渐稳定至60°～70°；小开度时，射流角对配合间隙的变化率很大，说明配合间隙对射流角影响很大；开度变大后，射流角对配合间隙的变化率逐渐变小，并且不同配合间隙的射流角越来越趋于一致，说明随着阀口开度增大，配合间隙对射流角度影响越来越小。相同开度下，随着配合间隙增大，射流角减小。结合图12、图13可知，当溢流阀与阀体之间存在配合间隙时，随着溢流压力增大，节流边阀口开度越来越小，射流角度越来越接近20°。

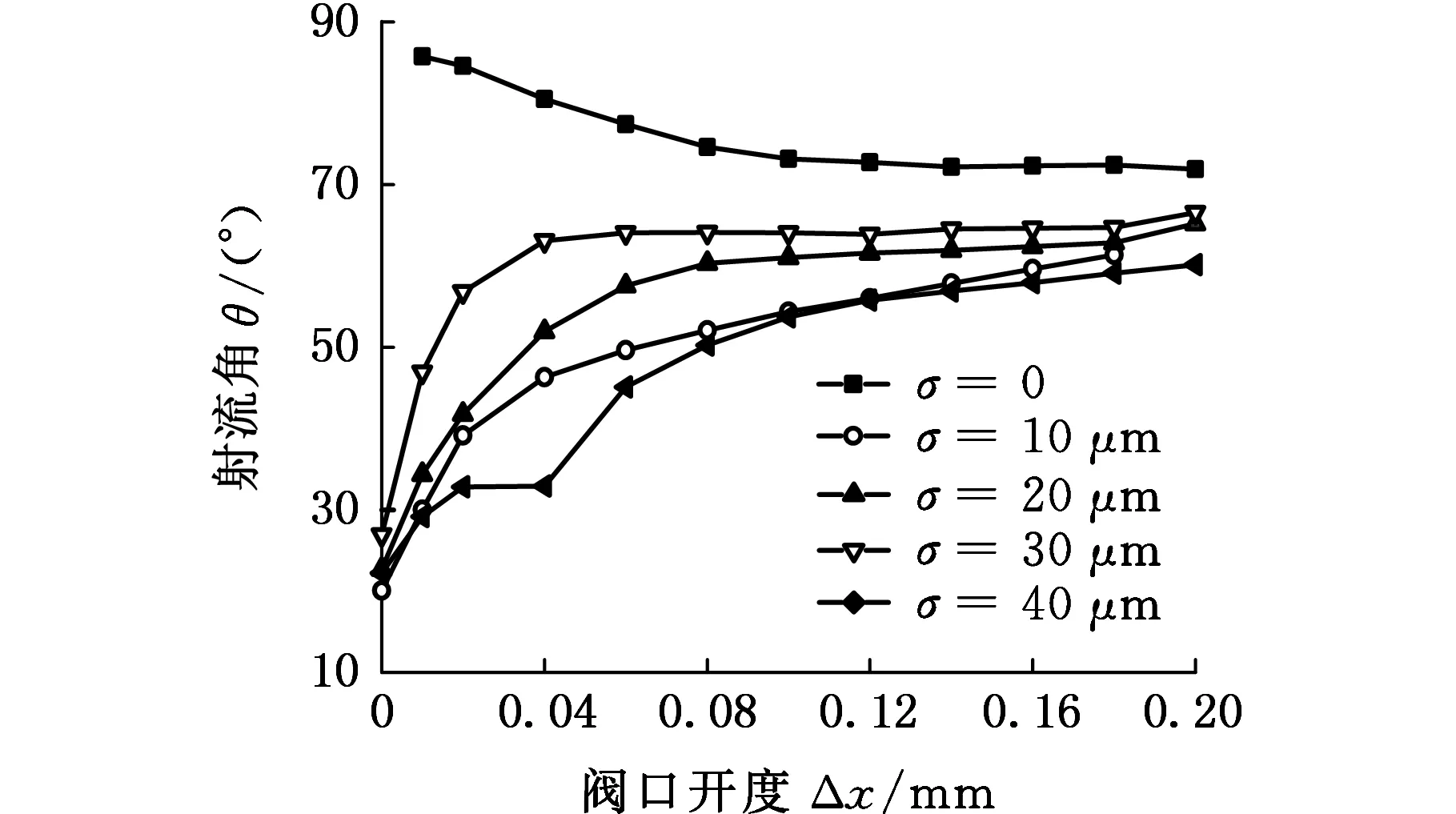
图13 射流角与滑阀开度的关系Fig.13 Relationship between jet angle and valve opening

4.3 配合间隙对稳态液动力的影响

图14 稳态液动力与溢流压力的关系Fig.14 Relationship between steady-state fluid force and relief pressure

利用式(2)计算出运动域在每一步产生的稳态液动力。图14所示为不同配合间隙下，阀芯受到的稳态液动力与溢流压力的关系，可以看出，配合间隙为0且溢流压力小于2.8 MPa时，液动力基本维持不变，溢流压力大于2.8 MPa后，液动力有减小趋势。当存在配合间隙且间隙小于20 μm时，液动力随着压力增大而线性增大；随着配合间隙增大，稳态液动力迅速增大。在配合间隙大于20 μm，且溢流压力低于某压力值时，液动力随着压力增大近似于线性增大，当溢流压力大于该压力值，稳态液动力基本保持不变；在低压段，随着配合间隙增大，液动力基本维持不变，在高压段，随着配合间隙增大，液动力越来越小。

5 结论

(1)通过对溢流阀液动力CFD仿真计算和与试验对比可知，考虑配合间隙的仿真结果与试验结果很接近，未考虑配合间隙的仿真结果与试验结果误差很大。因此，在做溢流阀液动力流体仿真时，不能忽略配合间隙的影响。

(2)溢流滑阀在工作过程中，节流边阀口开度很小，基本与配合间隙在同一数量级；阀口开度对溢流压力的变化率随溢流压力增大呈逐渐减小的趋势；在相同溢流压力下，配合间隙越大，阀口开度越小。

(3)相同阀口开度下，随着配合间隙增大，射流角度减小；在相同配合间隙下，射流角对阀口开度的变化率随着阀口开度增大慢慢变小；随着阀口开度增大，配合间隙对射流角度影响越来越小。存在配合间隙时，溢流阀工作压力越高，射流角越接近20°，因此在做溢流阀动力学仿真，尤其涉及液动力计算时，不能简单将射流角近似于69°。

(4)配合间隙在一定范围内，随着溢流压力升高，液动力线性增大，配合间隙增大，液动力明显增大。配合间隙大于某一临界值后，在小的溢流压力下，液动力随溢流压力增加呈线性增大趋势，随着配合间隙增加，液动力基本不变；在大的溢流压力下，液动力随溢流压力增大基本不变，随着配合间隙增大，液动力越来越小。

(5)鉴于配合间隙对溢流阀阀口开度、射流角以及液动力影响很大，在实际工程应用中，应设计合理的配合间隙尺寸，在避免滑阀卡滞和减小泄漏量的前提下，减小液动力对溢流阀的影响。

参考文献：

[1] GAD O. Comprehensive Nonlinear Modeling of a Pilot Operated Relief Valve[J]. Journal of Dynamic Systems，Measurement，and Control，2013，135(1)：011011.

[2] DASGUPTA K，WATTON J. Dynamic Analysis of Proportional Solenoid Controlled Piloted Relief Valve by Bondgraph[J].Simulation Modelling Practice and Theory，2005，13(1)：21-38.

[3] ZUNG P S，PERNG M H.Nonlinear Dynamic Model of a Two-stage Pressure Relief Valve for Designers [J]. Journal of Dynamic Systems Measurement & Control，2002，124(1)：62-66.

[4] LEE G S，SUNG H J，KIM H C，et al.Flow Force Analysis of a Variable Force Solenoid Valve for Automatic Transmissions[J]. Journal of Fluids Engineering，2010，132(3)：031103.

[5] 冀宏，傅新，杨华勇.非全周开口滑阀稳态液动力研究[J].机械工程学报，2003，39(6)：13-17.

JI Hong，FU Xin，YANG Huayong. Study on Steady Flow Force of Non-circular Opening Spool Valve [J]. Chinese Journal of Mechanical Engineering，2003，39(6)：13-17.

[6] 吴小锋，干为民，刘春节，等.液压换向滑阀内部结构的健壮性设计[J].中国机械工程，2015，26(15)：2030-2035.

WU Xiaofeng，GAN Weimin，LIU Chunjie，et al. Robust Design of Hydraulic Slide Valve Internal Structure[J].China Mechanical Engineering，2015，26(15)：2030-2040.

[7] YUAN Q，LI P Y.Using Steady Flow Force for Unstable Valve Design：Modeling and Experiments [J]. Journal of Dynamic Systems，Measurement，and Control，2005，127(3)：451-462.

[8] KRISHNASWAMY K，LI P Y.On Using Unstable Electrohydraulic Valves for Control[J]. Journal of Dynamic Systems，Measurement，and Control，2002，124(1)：183-190.

[9] 刘晓红，柯坚，刘桓龙.液压滑阀径向间隙温度场的CFD研究[J]. 机械工程学报，2006，42(s1)：231-234.

LIU Xiaohong，KE Jian，LIU Henglong，et al.CFD Research on Temperature Field in Radial Clearance of Hydraulic Spool Valve[J]. Chinese Journal of Mechanical Engineering，2006，42(s1)：231-234.

[10] PAN X D，WANG G L，LU Z S，et al.Simulation Research on Effect of Diametral Clearance of Spool Valve to Valve Orifice Discharge Characteristic [J]. Key Engineering Materials，2009，392/394：184-188.

[11] WEI M，YANG S，WU L，et al.Simulation and Experiment on the Flow Field in Fit Clearance for a Large Size Spool Valve[C]//International Conference on Fluid Power and Mechatronics.Beijing：IEEE，2011：748-751.

[12] 张晓俊，权龙，赵斌.内流式滑阀壁面压力分布可视化计算及试验验证[J].机械工程学报，2016，52(14)：196-203.

ZHANG Xiaojun，QUAN Long，ZHAO Bin. Visualization Calculation and Experimental Verification of Study Axial Flow Force on the Converged Flow Sliding Valve[J]. Journal of Mechanical Engineering，2016，52(14)：196-203.

[13] VAN DER MEULEN S， VAN IPEREN R， DEJAGER B，et al.A Validated Modular Model for Hydraulic Actuation in a Pushbelt Continuously Variable Transmission[J]. Journal of Dynamic Systems，Measurement，and Control，2011，133(4)：041004.

[14] 左健民.液压与气压传动[M].4版.北京：机械工业出版社，2005.

ZUO Jianmin.Hydraulic and Pneumatic Transmission [M].4 ed.Beijing：China Machine Press，2005.

[15] OKUNGBOWA N S.CFD Analysis of Steady State Flow Reaction Forces in a Rim Spool Valve[D]. Saskatoon：Univ. of Saskatchewan，2006.