机器人砂带磨削路径优化插补算法
2018-05-02张铁张斌
张 铁 张 斌
华南理工大学机械与汽车工程学院,广州,510641
0 引言
随着产业的发展,生产活动中对复杂曲面打磨加工的需求越来越多。然而传统手工砂带打磨方式的加工效率和精度较低,一个汽轮机叶片打磨需要熟练工人花费数个小时才能完成,且废品率很高[1];同时,打磨车间粉尘和噪声较大,严重危害了操作人员的健康。利用工业机器人代替人工打磨得到越来越多人的重视,机器人打磨加工的过程实质上就是机器人夹持工件,让曲面上的刀位点依次与磨轮上的加工点相接触,所以在被加工曲面上规划数量和间距合理的刀位点是机器人打磨的核心问题。
王伟等[2-3]在经典等参数线法[4]的基础上实现了弧长优化算法,避免了在曲率较大的过渡面上产生过切;李琳等[5]则基于平行截面法,利用一组平行面对工件的STL模型进行切片处理来生成曲面加工轨迹;LIN等[6]、FAROUKI等[7]利用泰勒展开推导出NURBS曲线的插补公式;刘强等[8]提出了无速度波动的NURBS割线二次插补,消除了泰勒展开过程中产生的截断误差以及插补过程中的弦逼近误差,保证了刀位点间的距离与设定时一致。陈志宇[9]在组合曲面上,利用等残高方法规划刀具路径。
上述研究主要通过等间距法、平行截面法和泰勒插补法生成加工轨迹上的刀位点。等间距生成刀位点时,需要凭经验确定刀位点的间距,可能造成刀位点的数目过多,降低了加工的效率;由平行截面法生成的刀位点密度取决于网格模型的精度,而且平行截面法的截面间距不易控制,在曲面平坦处、陡峭处生成的轨迹疏密不均;通过泰勒插补的方式获取刀位点时,曲率变化较大的区域适应性较差,产生的插补点数目过少而引起过切,严重影响了加工质量。因此上述算法均难以同时兼顾加工效率和加工质量。
本文主要针对曲率变化剧烈区域泰勒插补所引起的过切问题,对泰勒插补算法进行改进,减小加工误差,利用改进后的泰勒插补算法生成的刀位点能够同时兼顾加工效率和质量。
1 曲面磨削轨迹优化插补算法
在计算机的内部,复杂曲面一般定义在参数域上,其参数定义域通过一定的非线性映射关系得到曲面的表达,根据映射关系的不同可将曲面分为贝塞尔曲面、孔斯曲面、B样条曲面和NURBS曲面等。
本文采用NURBS曲面的参数线来生成磨削轨迹,在指定了被加工面之后,将该加工面以NURBS曲面的方式定义在u和v两个参数的参数域上。NURBS曲面的表达式[10]定义为
(1)
u∈[a,b]v∈[c,d]
式中,wi,j为控制点Pi,j的权值;n为u方向控制点数量;p为u方向曲面阶次;m为v方向控制点数量;q为v方向曲面的阶次;[a,b]、[c,d]分别是参数u和v的定义域。
固定NURBS曲面表达式中的一个变量不变,便可得到一条NURBS参数曲线,例如,分别固定参数v的值为v0、v1、v2、…,可以得到一组关于v的参数线加工轨迹,这组加工轨迹中相邻的两条加工轨迹所对应的参数v之间的增量Δv通过残留高度来确定,而每一条参数线轨迹上的刀位点则由插补算法来获取。
1.1 优化插补算法
1.1.1泰勒NURBS插补算法
一条k次NURBS曲线的有理分式形式定义如下[11]:
(2)
其中,wi是权因子,i=0,1,…,n;控制顶点为di,按顺序用直线段连接起来就是控制多边形;U为节点矢量,U=(u0,u1,…,un+k+1);Ni,k(u)是k次规范B样条基函数,其递推公式如下:
(3)
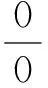
对NURBS曲线进行插补的实质就是确定每一个插补点对应的参数u。利用泰勒公式展开是NURBS插补中常用的算法,将u看成是时间t的函数,可得到二阶泰勒插补公式[5]:
(4)
式中,v(ti)、a(ti)分别为ti时刻的速度和加速度。
由于打磨加工的速度低且速度变化不大,故可忽略加速度的影响;式(4)中的速度v(ti)是NURBS曲线沿弧长的速度,而不是相邻两个插补点间直线段的速度,但相邻两个插补点之间的距离比较小,故可以用直线段来代替弧长,即v(ti)可看作是从Pi插补点到Pi+1插补点间直线段的速度,将该直线段的长度称为Pi插补点处的插补步长Li,则有
Li=(ti-ti+1)v(ti)
(5)
整理式(4)、式(5)并忽略加速度,可得到参数u的递推公式:
(6)
插补步长的选取对曲面的轮廓精度有很大影响,可以用近似圆弧替代附近NURBS曲线的方法来计算出插补步长,原理如图1所示。

图1 插补步长计算示意图Fig.1 Schematic diagram of interpolation step
ρi是曲线P(ui)点处的曲率半径,在曲线上建立Frenet标架,正则曲线的曲率半径计算公式为
(7)
δ0为设定的弓高误差,插补步长Li=|AB|,根据勾股定理可得

(8)
整理式(8)可以得到步长Li的计算公式:
(9)
将式(9)计算出的步长Li代入式(6)便可得到下一个插补点的参数ui+1。
1.1.2加工轨迹行距
曲面打磨轨迹的生成借鉴了数控加工中的等残高公式和参数线法,计算原理如图2所示,图中h为残留高度,w是等残高距离,P为当前轨迹(S(u,vj)参数线)的一个插补点,P*为插补点P根据等残高距离计算出的对应点,P*和P在同一条参数线S(ui,v)上。
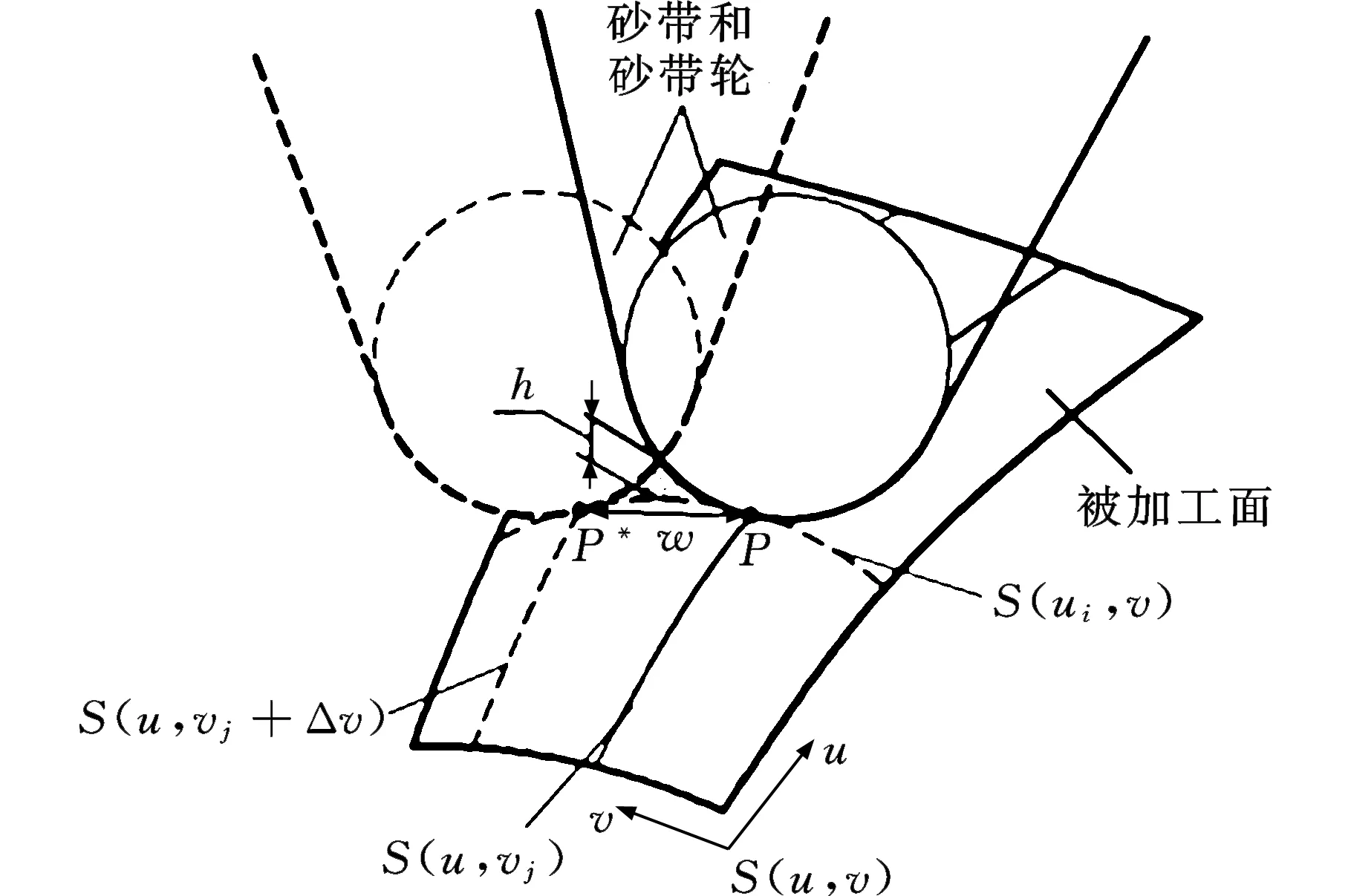
图2 磨削轨迹生成原理图Fig.2 Principle of grinding path generation
首先,利用等残高公式计算出当前轨迹线上所有插补点P及其对应的等残高点P*间的步距w和Δv,选择其中最小的Δv作为下一条轨迹线的参数增量;然后根据参数线法生成下一条轨迹线,以此类推,每一条轨迹的参数增量由上一条轨迹的插补点根据等残留高度公式求得。
凸面和凹面的等残高距离w如图3所示,P*和P之间用圆弧代替,ρP是u参数线在点P处的曲率半径,可利用式(7)计算求得,r为砂带轮的半径;对于凸曲面可以得到如下表达式:
[(r+ρP)sin(θ/2)]2+[(r+ρP)cos(θ/2)-
(ρP+h)]2=r2
(10)
整理后可得到图3a中凸曲面的等残高距离w的计算公式[12]:
(11)
同理,可得到凹面在插补点P处等残高距离的近似计算公式:
(12)

(a)凸面残留高度(b)凹面残留高度图3 等残高步距计算示意图Fig.3 Schematic diagram of constant scallop-height path
在得到插补点P处等残高距离w后,Δv的计算原理与插补点的计算原理一样,把w看成插补的步长,把曲线S(ui,v)看成被插补曲线P(v),将w代入式(6)中,变形得到Δv的计算公式:
(13)
1.1.3插补算法的优化
在推导1.1.1节的NURBS曲线插补递推公式时,用近似圆弧代替原曲线的方法来估算插补步长Li;然而这种近似是有前提条件的,即要求前后两个插补点P(ui)、P(ui+1)之间的原曲线段曲率变化不大;当曲线段的曲率有较大变化时,有可能会出现弓高误差超差的情况。如图4所示,插补步长Li通过式(9),由ui处的曲率半径ρi以及弓高误差设定值δ0来估算。曲线在点P(ui)处的曲率半径较大,会估算出较大的插补步长Li,这就有可能使得曲线段中该部分的刀位点数量密度不够(图5),曲率半径较小处的弓高误差δ超过设定值δ0而产生过切现象。

图4 弓高误差可能超差的情况Fig.4 The chord error is out of the tolarance

图5 曲率变化大时插补点密度过低Fig.5 The interpolation points are too sparse
改进的方法是,利用式(6)~式(9)计算出ui+1后,验算P(ui)P(ui+1)段轨迹曲线的中间点到割线段P(ui)P(ui+1)的距离δ是否小于设定的弓高误差δ0,如果P(ui)P(ui+1)段曲线的中间点到割线P(ui)P(ui+1)的距离δ都小于设定的弓高误差δ0,则以P(ui+1)为起点计算下一个插补点,否则将线段P(ui)P(ui+1)的长度乘以一个小于1的比例因子ε作为新的插补步长Li重新计算ui+1,直到所有验算中间点的δ都小于δ0,再计算下一个插补点,缩小因子ε的值根据超差验算点的位置来确定。中间点通过如下公式来选取:
Pk=P[ui+0.1k(ui+1-ui)]
(14)
k=1,2,…,9
其中,k是中间验算点的序号,k=1,2,…,9表示取9个中间点来进行验算。Pk到线段P(ui)P(ui+1)的距离:
(15)
步长优化插补算法的步骤如下:
(1)以被加工面的一条边界为第一条轨迹P(u),设置好弓高误差δ0以及残留高度h。
(2)判断轨迹P(u)是否在曲面上,如果否,则结束并返回;如果是,则将该刀路设置为当前轨迹,以当前轨迹的前端点参数值为当前插补点参数ui。
(3)计算当前插补点P(ui)处曲面的单位法向量以及轨迹曲线的单位切向量,然后将当前插补点的笛卡尔坐标、法向量和切向量存储在当前刀路的插补点链表中;判断ui是否是当前轨迹的末端点,如果是,则执行步骤(9);如果不是,则执行步骤(4)。
(4)由式(7)~式(9)计算出插补步长Li。
(5)由式(6)计算下一个插补点的参数ui+1。
(6)由式(14)来选取曲线段P(ui)P(ui+1)的中间点,利用式(15)来计算中间点到割线段P(ui)P(ui+1)的距离δk是否都小于设定的弓高误差δ0,如果是,则执行步骤(8);如果第k个中间点的δk超过了设定δ0,则执行步骤(7)。
(7)将割线段P(ui)P(ui+1)的长度‖P(ui)P(ui+1)‖乘以比例因子ε=0.1k以后作为新的步长Li,转至执行步骤(5)。
(8)将ui+1的值赋给ui,转至执行步骤(3)。
(9)利用式(11)、式(12)计算当前刀路所有插补点所对应的等残高距离w以及参数增量Δvi,选择最小的参数增量Δvi来计算下一条参数线轨迹P(u),输出当前插补点链表的数据至刀路文件,然后清空当前插补点链表,完成后转至执行步骤(2)。
1.2 刀位点坐标系建立
算法执行结束后,计算机可以输出一个包含被加工面上所有刀位点信息的.txt文件,称之为刀路文件;刀路文件每一行由9个数字组成,代表一个刀位点信息,前3个数字是刀位点在曲面笛卡尔坐标系{U}下的坐标(xi,yi,zi),中间3个数字是曲面在该刀位点处的单位法向量(ni,x,ni,y,ni,z),最后三个数字是刀位点所在轨迹在该点处的单位切向量(ti,x,ti,y,ti,z)。刀路文件的第i行代表第i个刀位点,其格式为
(xi,yi,zi,ni,x,ni,y,ni,z,ti,x,ti,y,ti,z)
(16)

(17)
2 机器人轨迹生成原理
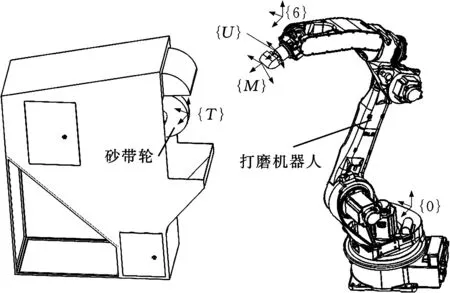
图6 机器人打磨系统坐标系的建立Fig.6 Coordinates for robot grinding system
(18)
打磨过程中,{M}和{T}会重合,即两个坐标系此时相对于基坐标系{0}有相同的描述:
(19)
结合式(18)、式(19)可得到如下关系式:
(20)
整理可得到
(21)

(22)
每一个刀位点坐标系{M}代入式(18)~式(22),便可以计算得到机器人打磨该刀位点时的关节空间位形,再将这些关节空间位形依照其对应坐标系的顺序组织成机器人控制柜可执行的程序,机器人执行程序完成工件的打磨。
3 仿真与试验
3.1 轨迹生成流程
本文的算法是在自主研制的机器人打磨离线编程系统中实现的,该离线编程系统生成机器人打磨轨迹的流程如图7所示。首先导入工件的IGES模型,选中被加工的曲面;然后设置弓高误差和残留高度,利用优化插补算法对曲面进行打磨刀路的规划并导出刀路文件;最后标定砂带轮上的工具坐标系,根据刀路文件中的数据建立一系列标架,再根据轨迹生成原理利用机器人逆解算法,求得实现这些标架与砂带轮固定工具坐标系依次重合的一系列关节空间位形,最终由这些关节空间位形转换成机器人轨迹程序。

图7 机器人打磨轨迹生成流程Fig.7 Process of robot grinding track generation
3.2 算法仿真
运用优化前后的插补算法在图8所示的零件上生成打磨刀位点。首先,生成图9所示的加工轨迹;然后设置弓高误差0.05 mm;最后,分别用优化前后的泰勒插补算法来获取加工轨迹上的刀位点。

图8 仿真曲面Fig.8 Surface used in simulation
图9 曲面加工轨迹Fig.9 Grinding path of the surface
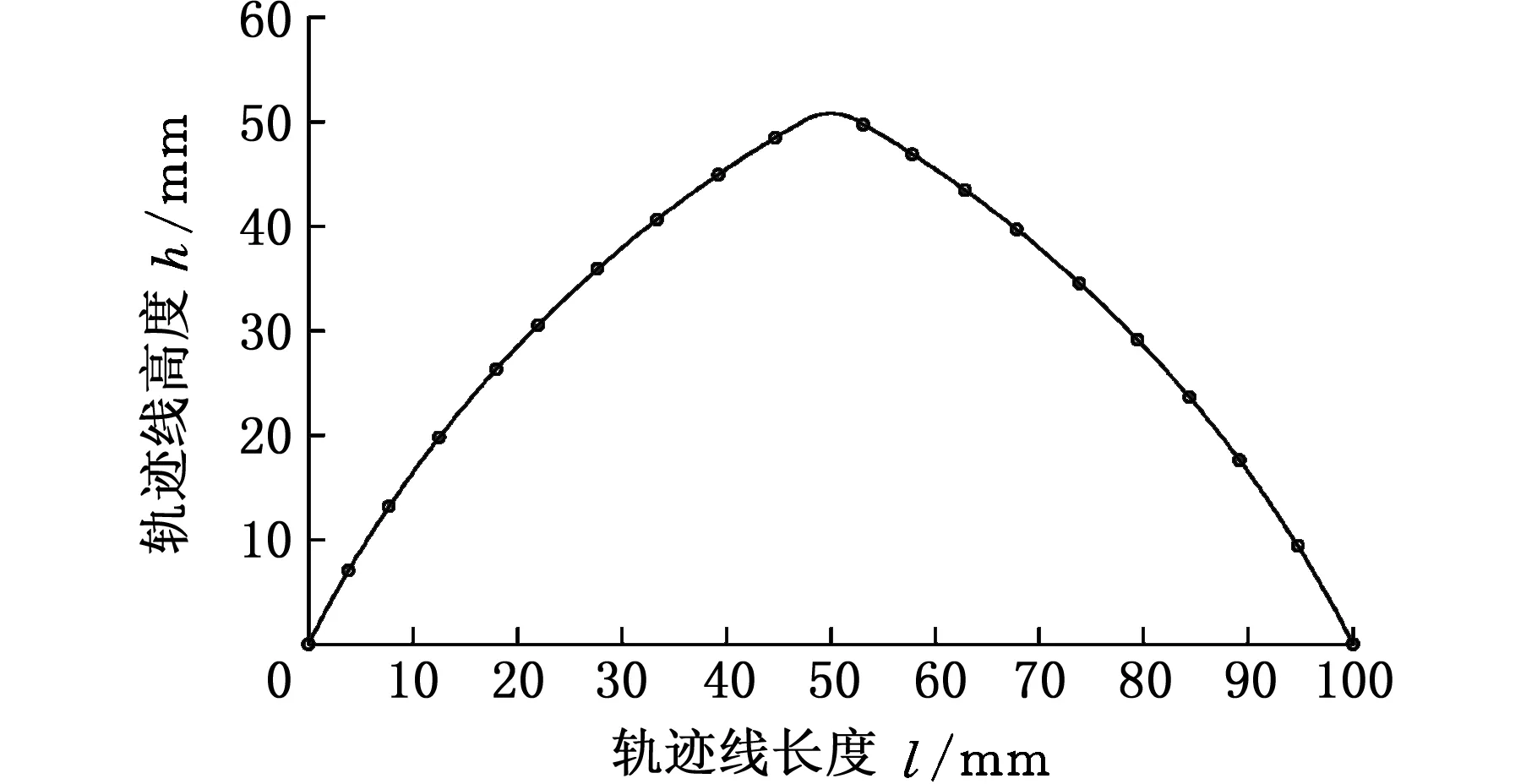
图10所示为两种插补算法在同一段加工轨迹上生成的刀位点,图11是两种插补算法弓高误差对比图。可以看出,在加工轨迹曲率变化较大的中间区域,优化算法所生成的刀位点较优化前的经典算法致密,而且弓高误差能够很好地控制在设定范围之内,保证了加工质量;在加工轨迹比较平滑的部分,优化算法产生的刀位点数量与经典算法相当,兼顾了加工的效率。
(a)经典算法生成的刀位点

(b)优化算法生成的刀位点图10 两种插补算法效果Fig.10 Results of two interpolation algorithms

(a)经典算法的弓高误差

(b)优化算法的弓高误差图11 弓高误差对比图Fig.11 Comparison of chord errors
3.3 试验验证
为了验证算法的有效性,设计了打磨加工对比试验,结果如图12所示。该试验采用MOTOMAN-MH24的机器人,型号是YR-MH00024-A00,末端负载能力为24 kg,重复定位精度为0.06 mm,机器人控制柜采用DX200标准规格;试验中使用小太阳TJ538型砂带,磨粒数目为120,打磨机接触轮的线速度为28.9 m/s;工件材料为45钢。下面针对图12所示的加工效果,以加工时间和形状误差两个方面作分析和比较。

(a)经典算法的加工效果(b)优化算法的加工效果图12 优化前后磨削效果对比Fig.12 Effect before and after optimization
3.3.1加工时间对比
离线编程系统根据图9所示的轨迹生成打磨程序,相邻两插补点所对应的机器人位姿之间采用直线插补方式,速度设定为11 mm/s。表1所示为优化前后插补算法生成的机器人程序行数和运行时间。可以看出,优化算法生成的刀位点数目较多,其程序的行数增大了60.46%,但是加工的时间只增加了不到5%,验证了优化算法兼顾了加工效率。

表1 程序行数和加工时间
3.3.2形状误差分析
利用三坐标测量仪器可测量出图12中两个零件被加工面上点的坐标。测量工具是Hexagon Brown & Sharpe Global三坐标测量仪,其精度是2 μm。
提取同一个截面的数据并与标准轮廓曲线在同一个坐标系下作图,可对2个零件的加工效果作形状误差分析,如图13所示,圆点代表用三坐标测量仪测量的该截面上的点,实线代表标准曲线,方框表示与标准曲线距离最大的数据点所在范围。表2所示为图13所示的数据点到标准曲线距离的最大值、平均值、中位数和标准差。表3所示为从零件上平均取5个截面所获得的数据点和标准轮廓的距离分布。
由图13和表2的数据可以看出,用优化前的轨迹加工零件会在轮廓曲线曲率变化较大的顶部产生严重过切,而运用优化后的轨迹进行加工,则可避免顶部位置过切的产生。
由表3的数据可以发现,运用优化过的算法进行打磨加工,其误差的平均值为0.121 mm,最大误差均值达到0.328 mm,比设定的弓高误差0.05 mm要高出许多;优化前的过切量平均值为1.403 mm,也比理论过切量0.953 mm要大。

(a)优化前

(b)优化后
图13 数据点与标准曲线
Fig.13 Data points and standard line

表2 数据点到标准曲线的距离
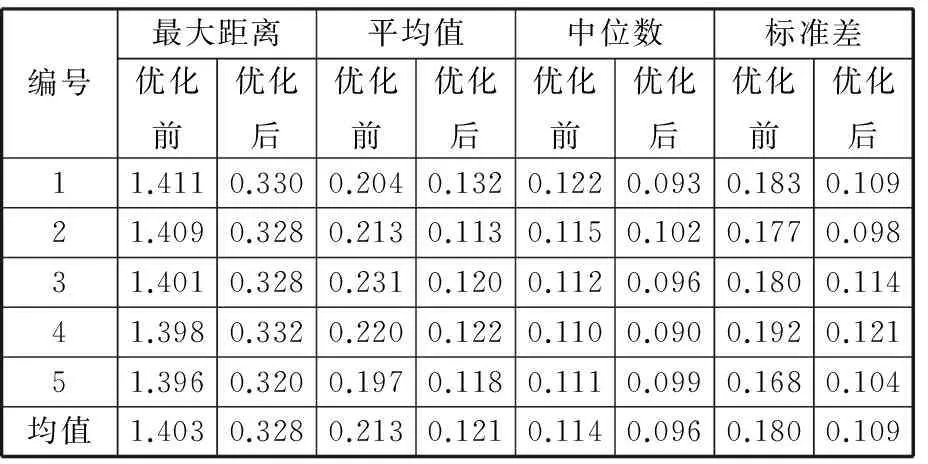
表3 5个截面的数据点和标准轮廓的距离
造成与理论计算值的差距主要原因有:①砂带打磨的接触轮是由橡胶材料制成的非刚性轮,当接触轮与工件接触的时有一定程度的变形。②机器人的开链结构刚度不足,在打磨过程中存在变形。本文第2节所述的机器人轨迹生成方法并没有考虑刚度的问题,到达某些位姿的关节量变化较大,一定程度上影响了机器人刚度。③打磨工具坐标系的标定误差。④工件的装夹误差和零件毛坯的形状误差。⑤机器人的重复定位误差。⑥砂带在加工中的损耗。
4 结论
(1)本文以经典的NURBS泰勒插补算法为基础,推导和实现了一种插补步长的优化算法,使得打磨路径上的刀位点数量在曲率变化较大的区域自适应地加大,而在较为平坦的区域插补点保持稀疏,与经典的泰勒插补算法相比,优化算法兼顾了磨削的效率和质量。
(2)在离线编程平台和实际砂带打磨试验中设计了对比试验,经典算法与优化算法生成打磨试件刀位点的弓高误差以及实际的磨削效果可以证明优化算法的可行性和有效性。
参考文献:
[1] NG T J,LIN W,CHEN X,et al. Intelligent System for Turbine Blade Overhaul Using Robust Profile Re-construction Algorithm[C]// 8th International Conference on Control , Automation , Robotics and Vision. Kunming,2004:178-183.
[2] 王伟,贠超.机器人砂带磨削的曲面路径优化算法[J].机械工程学报,2011,47(7):8-15
WANG Wei,YUN Chao. Optimization Algorithm for Robotic Belt Surface Grinding Process[J]. Journal of Mechanical Engineering, 2011,47(7):8-15.
[3] WANG Wei, YUN Chao. A Path Planning Method for Robotic Belt Surface Grinding[J]. Chinese Journal of Aeronautics , 2011 (24):520-526.
[4] 张任俊,王洪申. 复杂曲面数控加工刀具轨迹规划技术研究进展[J].机械制造, 2016,45(2):9-12.
ZHANG Renjun,WANG Hongshen. Research and Development of Tool Path Planning Techniques for NC Machining of Sculptured Surfaces[J] . Machine Building &Automation, 2016,45(2):9-12.
[5] 李琳,黎润伟.复杂曲面加工工业机器人轨迹生成算法[J].机械设计与制造,2013,11(11):175-178
LI Lin,LI Runwei. Algorithm of Industrial Robot on Path Generation for Complex Surface Machining[J]. Machinery Design & Manufacture, 2013,11(11):175-178.
[6] LIN Ming-Tzong, TSAI Meng-Shiun. Development of a Dynamics-based NURBS Interpolator with Real-time Look-ahead Algorithm[J]. International Journal of Machine Tools & Manufacture, 2007,47: 2246-2262.
[7] FAROUKI R T, TSAI Y F. Exact Taylor Series Coefficients for Variable-feedrate CNC Curve Interpolators[J]. Computer-Aided Design, 2001,33(2): 155-165.
[8] 刘强,刘焕.无速度波动的NURBS曲线二次插补算法原理及其实现[J]. 计算机集成制造系统,2015,21(10):2659-2667.
LIU Qiang ,LIU Huan. Principle and Development of NURBS Interpolation Algorithm with Zero-feedrate Fluctuation[J]. Computer Integrated Manufacturing Systems, 2015,21(10):2659-2667.
[9] 陈志宇.组合曲面等残高刀具路径规划方法研究及实现[D]. 杭州:浙江大学,2014.
CHEN Zhiyu. Research on Constant-Scallop Height Tool Path Planning Method on Compound Surface[D]. Hangzhou:Zhejiang University,2014.
[10] 王汝传,黄海平.计算机图形学教程[M]. 2版.北京:人民邮电出版社,2009.
WANG Ruchuan, HUANG Haiping. Computer Graphics [M]. 2ed. Beijing: Posts & Telecom Press, 2009.
[11] LES P, WAYNE T. The NURBS Book[M]. 2 ed. New York:Springer-Verlag, 1997.
[12] 张海洋. 叶片砂带磨削机器人轨迹规划与离线编程[D]. 武汉:华中科技大学,2014.
ZHANG Haiyang. Robotic Trajectory Planning and Off-line Programming for Belt Grinding of Turbine Blade[D].Wuhan:Huazhong University of Science and Technology,2014.
