基于全矢谱时间固有尺度分解和独立分量分析盲源分离降噪的滚动轴承故障特征提取

刘嘉辉 董辛旻 李剑飞

郑州大学机械工程学院，郑州，450001

0 引言

滚动轴承广泛应用于各种旋转机械中，它的工作状态与机械的运行效率和使用寿命息息相关，因此对滚动轴承进行故障特征提取与诊断十分必要。滚动轴承的故障信号特点是非线性非平稳，信号不仅微弱、调制性强而且频带大多比较宽。由于受复杂背景噪声等影响，滚动轴承故障信号常常湮没于噪声中。传统的轴承故障特征提取方法对提取滚动轴承的故障特征效果不佳[1-2]。

盲源分离技术根据故障以及噪声信号的相对独立性，能够提取完全湮没于噪声中的有用信号，实现对观测信号的噪声去除[3]。全矢谱技术建立在全信息技术基础上，针对全谱和全息谱的局限性提出了同源多维分析体系，其优势体现在对旋转机械同源信息的充分利用与融合，从多角度、全方位研究信息能量，使得全矢谱的图谱具有和传统分析方法同样好的分辨率和动态范围，并且能够进一步做能量分析[4-5]。

本文将盲源分离与全矢谱相结合，采用ITD-ICA盲源分离法除去轴承故障信号中的噪声，将同源双通道的振动信号进行时间固有尺度分解(inherent time scale decomposition，ITD)，利用相关系数准则将分解得到的PRC(proper rotation components)分量进行重组及构建虚拟噪声，采用FastICA解混，实现故障信号与噪声信号的分离。再对去除噪声后的故障信号进行全矢希尔伯特包络分析，融合同源信息，提取滚动轴承故障特征信息。实际滚动轴承故障实验结果表明，该方法的轴承故障特征提取效果显著。

1 时间固有尺度分解

时间固有尺度分解(ITD)能将信号分解成多个固有旋转分量PRC与一个趋势分量r之和。分别对PRC的瞬时频率和幅值进行频谱分析，可分别得到信号调频和调幅特征。某信号Gt，一次ITD分解把信号Gt分解成单个基线分量Lt与单个固有旋转分量Ht，即

Gt=LGt+(1-L)Gt=Lt+Ht

(1)

式中，L为定义的基线提取因子；Lt为基线信号，Lt=LGt；(1-L)Gt为固有旋转分量，代表信号局部相对高频成分。

令Gk、Lk分别表示G(tk)、L(tk)；设Lt、Ht在[0,τk]上有定义，Gt在[0,τk+2]上有定义，那么在连续极值点间隔τk、τk+1上可定义这个区间内Gt的分段线性基线提取因子L：

(2)

(3)

式中，α为用于控制提取固有转动分量幅度的线性缩放因子，α∈(0，1)，一般取α=0.5。

把基线分量看作新的待分解信号，不断重复以上分解过程，即可得到一系列固有旋转分量PRC，至分解为一个单调的趋势信号为止。此过程将原始信号Gt分解为若干从高到低不同频率段的固有旋转分量之和与一个单调趋势分量。整个ITD分解过程如下：

(5)

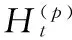
2 独立分量分析

独立分量分析(independent component analysis，ICA)为高阶循环统计量方法，在没有任何先验知识统计独立性的前提下，将原始信号从多重观测到的信号中分离出来，将隐藏在观测信号中的独立源成分提取出来。

设n个观测信号X=(x1,x2,…,xn)T，为m个独立的信号S=(s1,s2,…,sn)T的线性混合

X=AS

(6)

其中，A为n×m的未知混合矩阵。

盲源分离从观测信号中恢复出源信号，即要找出一个分离矩阵W将相互独立的源信号从混合信号中分离出来，即

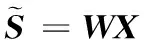
(7)

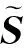
FastICA算法又称固定点(FixedPoint)算法，是基于定点递推算法而得的，可使收敛更快更稳健[7]，适用于任何类型数据，也可用于分析高维数据。

3 全矢谱分析

来自转子同一截面x、y两个方向的振动信息属于同源信息，全矢谱技术就是在转子同一截面上同时布置两个相互垂直的传感器对信号进行采集和融合分析。全矢谱分析的基本指导思想是：转子的涡动现象是各谐波频率下组合作用的结果，其涡动轨迹是一个椭圆，定义这些椭圆的长轴长度为振动强度评价的主振矢，短轴长度为振动强度的副振矢，转子在各谐波频率下的涡动强度是对故障判断和识别的基本依据[8]。椭圆是两个频率(ψ)相同、运动方向(角速度为ω)相反的圆轨迹的合成，如图1所示。

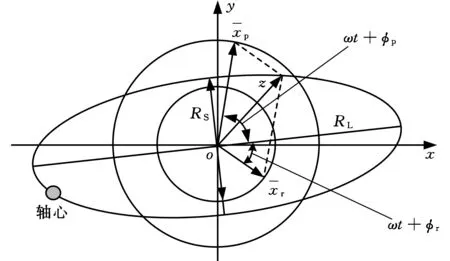
图1 椭圆轨迹与分解成的正反进动圆Fig.1 The elliptical trajectory and its decomposedpositive and negative precession circles

由图可知，将椭圆轨迹引入复平面，用复数点z(z=x+jy)来表示椭圆上的任意一点，即

(8)

具体推导过程见文献[5]，这里不再赘述。

假定x方向上采集的离散信号为{xn}，y方向上采集的离散信号为{yn}(n=0,1,…,N-1)。分别对{xn}和{yn}进行傅里叶变换得到{Xk}、{Yk}(k=0,1,…，N-1)，N为信号长度，XRk、YIk、YRk、YIk分别为Xk，Yk的实部和虚部序列。{xn}和{yn}构造复序列{zn}{xn}+j{yn}，对{zn}做快速傅里叶变换，得到离散序列{Zk}。根据快速傅里叶变换的性质有如下关系：

(9)

由式(8)～式(9)得：

(10)

以上实现了通过两个通道的数据序列做一次傅里叶变换,从而得到全矢谱需要的各谐波轨迹的特征信息，大大减小了计算量，同时也非常稳定[9-10]。

4 全矢ITD-ICA特征提取方法

ICA算法进行盲源分离降噪通常是单通道信号且观测信号源数目不少于信号源数，针对此问题，本节提出的这种方法将水平垂直两方向双通道采集的振动信号分别进行ITD分解，根据相关系数准则构建虚拟噪声通道，再利用FastICA解混矩阵，实现信噪分离后做全矢谱分析提取故障特征。这不仅有效解决了信噪盲源分离中ICA的欠定问题，而且双通道采集信号可使提取的故障信息更加完整。此方法具体实现步骤如下：

(1)分别对同一振动信号进行水平方向和垂直方向采样，得到双通道的采样信号。

(2)对双通道的采样信号分别进行ITD分解，得到若干分量PRC。

(3)将得到的双通道的PRC分量分别根据互相关系数准则选择与观测信号相关程度较大的PRC分量进行重构，而其余分量构建虚拟噪声。

(4)采用FastICA算法对混合后的重构信号和虚拟噪声信号进行解混，得到信噪分离后的ICS分量。

(5)分别对双通道降噪后的ICS分量信号进行全矢谱分析，从而提取轴承故障特征。

全矢谱ITD-ICA方法流程如图2所示。

图2 算法流程图Fig.2 The algorithm flow chart

5 滚动轴承实验分析

本文采用美国西储大学滚动轴承故障实验数据[11-12]进行实验分析，实验系统如图3所示。实验系统的电机转速为1 796 r/min，采样频率为12 000 Hz，选择驱动端的滚动轴承型号为SKF6205深沟球轴承，其技术参数和规格信息如表1所示。选择电火花加工在电机驱动端布置的轴承单点故障，故障位置分别为3点钟水平方向和6点钟垂直方向，点蚀故障直径为0.533 4 mm，深度为0.279 4 mm。

根据表1的各参数信息，通过计算可得到轴承内圈、外圈和滚动体的故障频率，如表2所示。选择轴承外圈3点钟和6点钟方向故障(即水平方向故障和垂直方向故障)信号的采样点数为4 096，信号时域图见图4。

图3 实验装置系统Fig.3 The experimental device system

内圈直径(mm)外圈直径(mm)滚动体直径(mm)接触角(°)滚动体个数25.0052.007.9409

表2 滚动轴承各部件故障特征频率

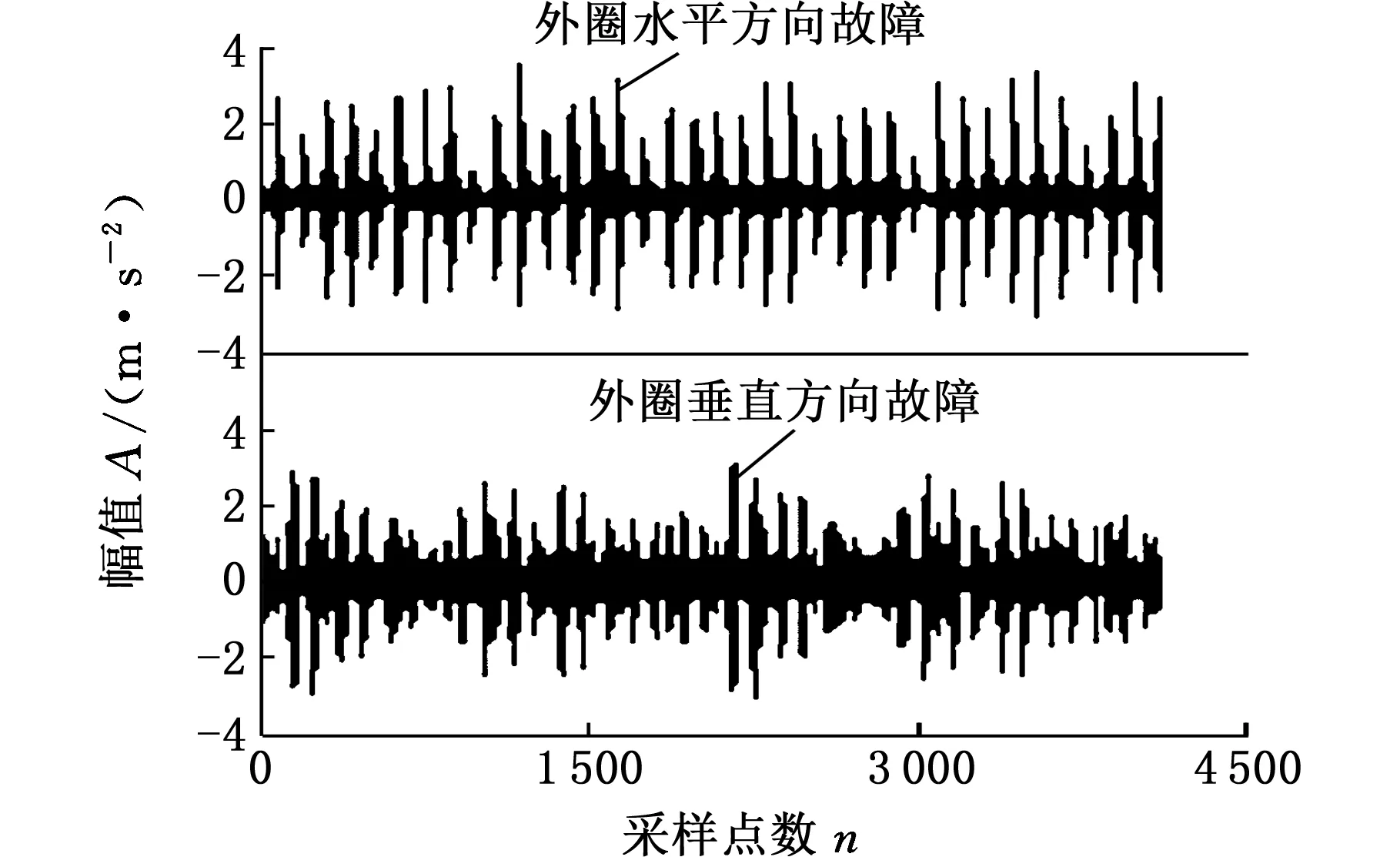
图4 外圈水平和垂直方向时域信号Fig.4 Horizontal and vertical signals of outer ring

将原始水平和垂直两个方向的时域故障信号分别进行ITD分解后得到若干PRC分量，这里只取前四个分量和一个残余分量进行分析，如图5所示。

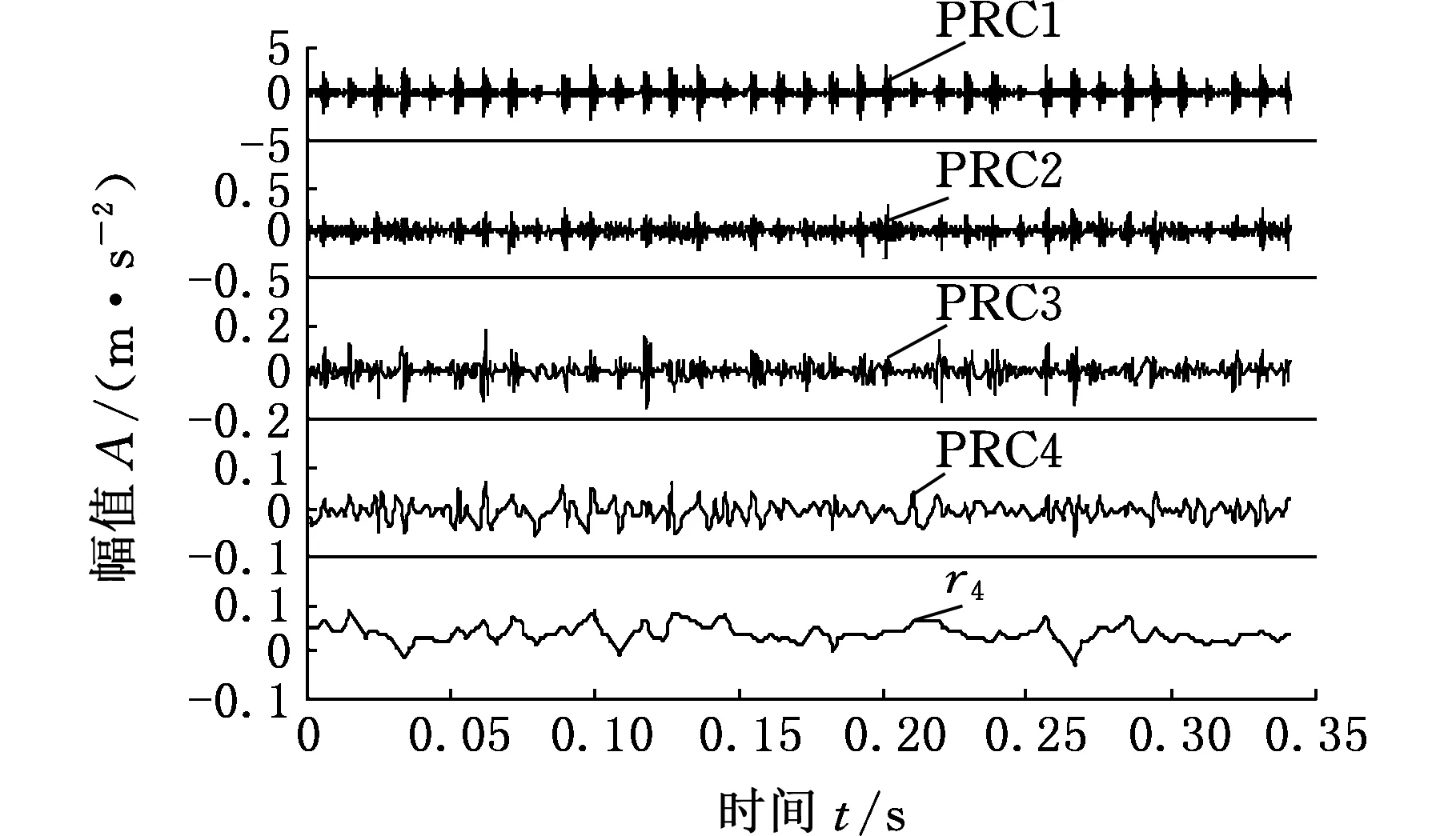
(a)水平方向各PRC分量信号

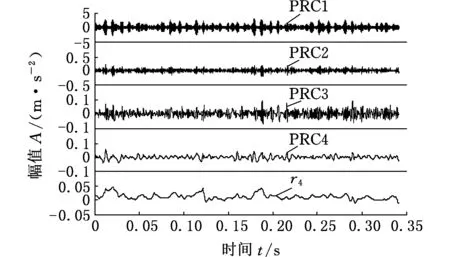
(b)垂直方向各PRC分量信号图5 水平和垂直方向各PRC分量信号Fig.5 Horizontal and vertical PRC component signal

分别计算水平方向和垂直方向各PRC分量信号与原始信号的相关系数，如表3所示。

由表3可知，PRC1、PRC2与源信号相关系数较大，PRC3，PRC4与源信号相关系数较小，故将其重组构建虚拟噪声通道，将相关系数较大的重组信号和噪声重组信号都作为FastICA的输入通道，通过ICA解混得到x、y两方向的独立分量(IC)时域图，如图6所示。

表3 水平和垂直方向PRC分量与源信号相关系数

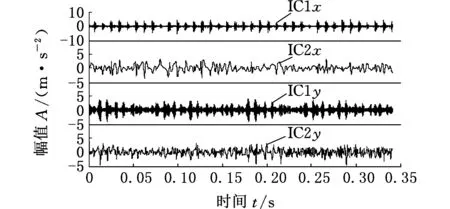
图6 x、y方向各独立分量时域图Fig.6 Time domain of independent components of x and y

对x、y方向ICA分解所得各独立分量(IC)信号进行希尔伯特包络分析，如图7所示。由图7a可看出，水平方向x的分量IC1轴承外圈故障频率f=108.4 Hz，转频为29.3 Hz，二倍频f=213.9 Hz，三倍频f=322.3 Hz，故障频率及倍频特征明显，而分量IC2无明显故障频率特征，是噪声信号，被有效分离出来。由图7b可知垂直方向y的分量IC1轴承外圈故障频率f=108.4 Hz，二倍频f=216.8 Hz，四倍频f=430.7 Hz，与x方向相比故障倍频有细微差别，而分量IC2也无明显故障频率特征，噪声信号得以分离。图7说明轴承x、y方向的故障特征存在差异，说明轴承不同方位所呈现的故障存在细微差别，单方向单通道信号不能全面反应轴承的故障特征。

(a)x方向ICA分量包络谱

(b)y方向ICA分量包络谱图7 x、y方向ICA分量包络谱Fig.7 Envelope spectrum of ICA components of x and y

分别对x、y方向两通道信号信噪分离后的两个分量IC1x、IC2x进行同源信息融合的全矢希尔伯特包络分析，如图8所示。由图8可以看出，轴承外圈转频、故障特征频率及各个倍频与理论计算所得故障频率和倍频更接近，故障特征更明显，并且包含更完整的故障信息，故障特征频率可达九倍频处。

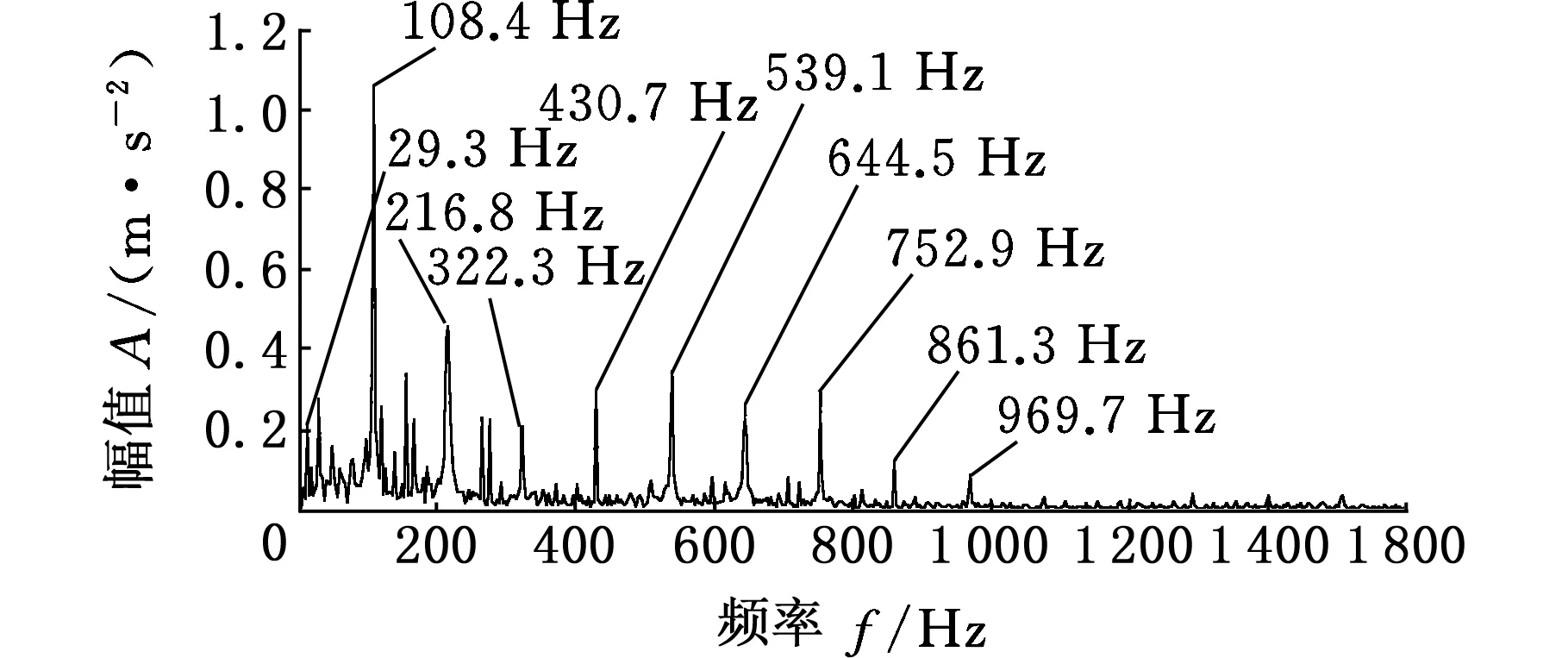
图8 全矢希尔伯特包络谱Fig.8 Full vector Hilbert envelope spectrum

图9 有效ICA分量包络谱Fig.9 Envelope spectrum of effective ICA components

为了说明此方法的优越性，图9采取只对单通道ITD和ICA信噪分离后的有效ICS分量进行包络分析。由图9可知，轴承故障频率在一倍频、二倍频和四倍频处较为明显。

对比图8和图9可以看出，对信噪分离后的有效分量ICS做全矢谱的分析，提取出的轴承故障频率可至九倍频处，故障特征更显著。

6 结论

采用全矢ITD-ICA方法对双通道轴承故障同源信号进行盲分离降噪处理，再对其做全矢希尔伯特包络谱分析可使故障特征更显著，能够更有效地提取出轴承的故障特征。对比轴承单通道信号降噪处理和希尔伯特包络分析实验，所提方法解决了单通道信号故障特征提取效果不明显、故障信息不完整的问题。不足的是该方法在双通道采集信号时要求同一轴承的同源信息采集，后续才能有效进行全矢信息融合和全矢谱分析，对于不同源采集到的振动信号不可用，具有一定的局限性，需要进一步研究。

参考文献：

[1] 陈恩利,张玺,申永军,等.基于SVD降噪和盲信号分离的滚动轴承故障诊断[J].振动与冲击,2012,31(23):185-190.

CHEN Enli, ZHANG Xi, SHEN Yongjun, et al. Fault Diagnosis of Rolling Bearings Based on SVD De-noising and Blind Signals Separation[J].Journal of Vibration and Shock,2012,31(23):185-190.

[2] 柏林,陆超,赵鑫,等.基于ITD与ICA的滚动轴承故障特征提取方法[J].振动与冲击,2015,34 (14): 153-156.

BO Lin, LU Chao, ZHAO Xin, et al. Fault Diagnosis Method for Rolling Bearings Based on ITD and ICA[J].Journal of Vibration and Shock,2015,34 (14): 153-156.

[3] 李晓晖,傅攀.基于EEMD的单通道盲源分离在轴承故障诊断中的应用[J].中国机械工程，2014,25(7):924-930.

LI Xiaohui, FU Pan. Application of Single-channel Blind Source Separation Based on EEMD in Bearing Fault Diagnosis[J].China Mechanical Engineering，2014, 25(7):924-930.

[4] 韩捷,张瑞林.旋转机械故障机理及诊断技术[M].北京:机械工业出版社,1997:85-89.

HAN Jie, ZHANG Ruilin. Fault Mechanism and Diagnosis Technology of Rotating Machinery [M].Beijing: Machinery Industry Press, 1997:85-89.

[5] 韩捷,石来德.全矢谱技术及工程应用[M].北京: 机械工业出版社, 2008:92-99.

HAN Jie, SHI Laide. Full Vector Spectrum Technology and Its Engineering Application [M].Beijing: Machinery Industry Press, 2008:92-99.

[6] 胥永刚，陆明，谢志聪．基于固有时间尺度分解的能量算子解调法及故障诊断应用[J].海军工程大学学报，2013，25(1) :27-31．

XU Yonggang, LU Ming, XIE Zhicong. Teager Energy Operator Demodulation Method Based on ITD and Its Applications in Fault Diagnosis [J].Journal of Naval University of Engineering, 2013,25(1):27-31.

[7] 李力.机械信号处理及其应用[M].武汉：华中科技大学出版社，2007:92-98.

LI Li. Mechanical Signal Processing and Its Application[M]. Wuhan:Huazhong University of Science and Technology Press, 2007:92-98.

[8] 李志农,王心怡,张新广,等.基于全矢谱核函数主元分析的旋转机械故障诊断方法研究 [J].振动与冲击，2008，27(7):55-57.

LI Zhinong, WANG Xinyi, ZHANG Xinguang, et al. Fault Diagnosis of Rotating Machinery Based on Full Vector Spectrum Kernel Principal Component Analysis[J].Journal of Vibration and Shock,2008,27(7):55-57.

[9] 韩捷，巩晓赟，陈宏.全矢谱技术在齿轮故障诊断中的应用[J].中国工程机械学报，2010,8(1):81-85.

HAN Jie, GONG Xiaoyun, CHEN Hong. Application of Full Vector Spectrum Technology in Gear Fault Diagnosis[J].Chinese Journal of Construction Machinery,2010,8(1):81-85.

[10] 韩捷,王宏超,陈宏,等.滚动轴承故障的全矢小波分析[J].轴承，2011(3):45-47.

HAN Jie, WANG Hongchao, CHEN Hong, et al. Full Vector Wavelet Analysis of Rolling Bearing Fault[J].Bearing，2011(3):45-47.

[11] 卞家磊，朱春梅，蒋章雷，等.LMD-ICA联合降噪方法在滚动轴承故障诊断中的应用[J] 中国机械工程，2016,27(7):904-910.

BIAN Jialei, ZHU Chunmei, JIANG Zhanglei, et al.Application of LMD-ICA to Fault Diagnosis of Rolling Bearings[J]. China Mechanical Engineering, 2016,27(7):904-910.

[12] ŽVOKELJ M, ZUPAN S, PREBIL I. Multivariate and Multiscale Monitoring of Large-size Low-speed Bearings Using Ensemble Empirical Mode Decomposition Method Combined with Principal Component Analysis[J]. Mechanical Systems & Signal Processing, 2010, 24(4):1049-1067.