基于离散广义S变换与双向二维主成分分析的内燃机故障诊断

张世雄 蔡艳平 石林锁 王 旭

火箭军工程大学，西安，710025

0 引言

受旋转部件和往复运动部件的惯性作用力影响，内燃机系统的激励与响应呈现出非线性、非平稳性的特征，因此，在旋转机械设备状态监测与故障诊断中的许多成熟技术不能很好地推广到内燃机故障诊断中去。如何从复杂多变的系统响应中提取故障信息并对其进行准确识别，一直是相关研究的热点与难点。

目前，利用时频表征方法将内燃机振动信号生成时频图像来进行模式识别已得到广泛的应用和认可。文献[1]通过对小波降噪后的非平稳信号进行短时傅里叶变换(STFT)，实现对主轴振动特征的准确提取。文献[2]将小波包振动谱图像用于柴油机故障诊断实例，达到了较高的识别率。此外，魏格纳时频分布[3]、自适应最优核时频分布[4]以及S变换[5-6]在振动谱图像生成方面也得到广泛的研究。其中，S变换是在STFT和小波变换(WT)的基础上发展而来的，不仅弥补了STFT中单一分辨率的问题，而且保留了小波变换所不具备的相位信息[7]。然而，将一维函数映射为一个二维函数后，在二维平面上往往会存在信息的冗余[8]。离散广义S变换可利用二维平面上的离散栅格实现对原信号的重构，不仅可消除信号处理中的信息冗余，而且可以提高时频图像的聚集性。

图像特征提取是模式识别中的关键环节，将主成分分析技术[9]用于机械设备的故障诊断获得了广泛的研究。文献[10]提出的二维主成分分析(2DPCA)避免了将图像矩阵转化成向量进行处理的问题，使运算更加便捷。文献[11]在2DPCA的基础上引入图像分块的思想，使提取后的特征系数矩阵类间散度更大，类内散度更小。然而，前几种特征提取方法只是对图像进行单向压缩，故均存在特征维数较大的问题。文献[12]在轴承故障研究当中采用双向二维主成分分析(two-directional two dimensional principal components analysis，TD-2DPCA)技术大大缩减了特征维数，在保证识别率的同时，极大地提高了运算速度。

针对内燃机气阀机构的故障诊断研究，本文提出一种结合离散广义S变换与TD-2DPCA的诊断方法，将其应用于气阀机构8种不同状态的分类识别。对比2DPCA、二维线性判别分析(2DLDA)[13]以及基于模块的2DPCA可知，本文所提算法具有计算速度快、识别精度高的优势。

1 离散广义S变换与TD -2DPCA的诊断方法

1.1 内燃机信号离散广义S变换时频表征

离散广义S变换是标准S变换的推广，通过在窗函数中引入调节参数k、p改变窗口变化速度，使得“基函数”与信号达到更佳的匹配，提高时频聚集性。同时，离散化的广义S变换可减少二维平面内信息的冗余，在不损失信息量的前提下，大大减小计算量和存储空间。

在能量有限空间L2(R)中，若x(t)∈L2(R)，则信号x(t)的S变换定义为

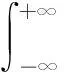
(1)

其中，τ为时移因子，f为频率，w(t)为高斯窗，窗函数标准差σ(f)=1/|f|。由式(1)可以看出，随着信号频率的增加，窗函数宽度会减小。为增强标准S变换中窗函数的适应性，在其标准差σ(f)中引入两个调节因子k、p，则

σ(f)=k/|f|p

(2)

此时，窗函数为

(3)

由此可得信号广义S变换的定义：

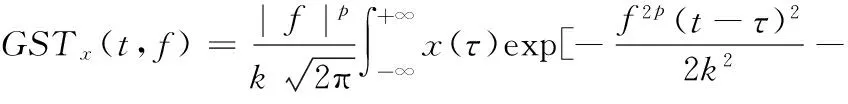
(4)

利用傅里叶变换和卷积定理与式(4)类似推理过程，可得

(5)

其中，X(α+f)为信号x(t)的傅里叶变换并平移频率α。将式(5)离散化，令f→n/(NT)，τ→jT，T为采样间隔，N为采样点数，则信号x(t)的离散广义S变换为

(6)

式中，j代表时间，j=0，1，…，N-1；n代表频率，n=0，1，…，N-1。

特别地，n=0时的离散广义S变换定义为

(7)

由式(7)可见，离散广义S变换可以用快速傅里叶变换(FFT)和卷积定理来实现。

1.2 TD-2DPCA图像特征提取

TD-2DPCA本质上是对图像数据重新编码，使特征维数进一步约减，从而极大地减小运算量，提高计算效率。

假设有c类模式w1、w2、…、wc，M个训练样本图像A1、A2、…、AM，每个图像大小为u×v，则训练样本的总体散度矩阵为

(8)

式中，Gt为v×v维的非负定矩阵。

因此可得，矩阵Gt有v个标准正交的特征向量：

GtXi=λiXi

(9)

λ1≥λ2≥…≥λn≥0

其中，Xi为v维单位化的列向量。为提高多分类样本的区分度，取矩阵Gt的前d个特征值所对应的特征向量构成最优投影矩阵P=[X1X2…Xd]。图像样本矩阵A通过投影得到特征系数矩阵B，B=AP。此时特征系数矩阵的维数为u×d，只达到了对图像进行横向压缩的目的，若想进一步减小矩阵维数，可从纵向对特征系数矩阵再次进行压缩。

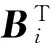
(10)

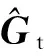
U=ΒT[Z1Z2…Zh]=PTATQ

(11)

此时U的维数为h×d，与原图像矩阵维数u×v相比，数据计算量得到了有效的缩减。

1.3 诊断流程

基于离散广义S变换和TD-2DPCA的内燃机故障诊断流程如图1所示。为方便对比，分别采用标准S变换及离散广义S变换将诊断实例中的内燃机缸盖振动信号生成时频图像，然后通过4种不同的特征提取方法对图像进行特征提取，最后利用最近邻(NNC)分类器进行分类识别。

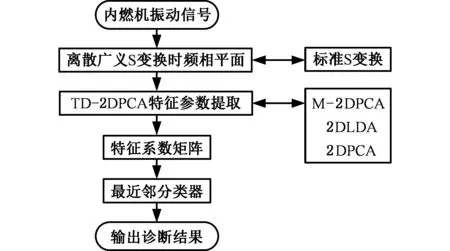
图1 故障诊断流程Fig.1 Flowchart of fault diagnosis

2 诊断实例

2.1 内燃机实验工况

数据来源为6135G型柴油机，现场采集平台，实验中采用QY8051622型光电转速传感器测量第2缸缸盖的上止点信号，L14型压电式加速度传感器测量缸盖的振动响应信号，传感器的布置方式如图2所示。采集过程中，采样频率为25 kHz，转速为1 500 r/min，且空载运行。

图2 光电转速传感器与加速度传感器布置方式Fig.2 Installation locations of photoelectric speed sensor and acceleration sensor

实验模拟了气阀机构常见的8种工况：气门间隙过小、间隙过大、轻微漏气、严重漏气等。具体数据见表1。其中，0.06 mm、0.3 mm和0.5 mm分别代表气门间隙过小、正常、过大，以排气门上4 mm×1 mm的开口模拟严重漏气。“新气门”表示气门未经研磨，模拟气门轻微漏气。实验采集8种工况各60组信号，共480个。

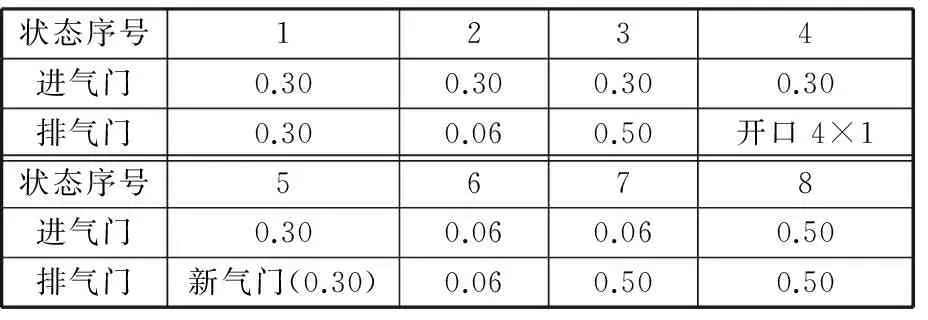
表1 内燃机8种工况参数设置

2.2 内燃机缸盖振动信号时频分析

首先取气阀机构正常状态下的振动信号，通过离散广义S变换生成振动谱图像。为描述正常状态下气体燃烧效率，同时将信号的时域图以及功率谱图一并给出，结果如图3所示。

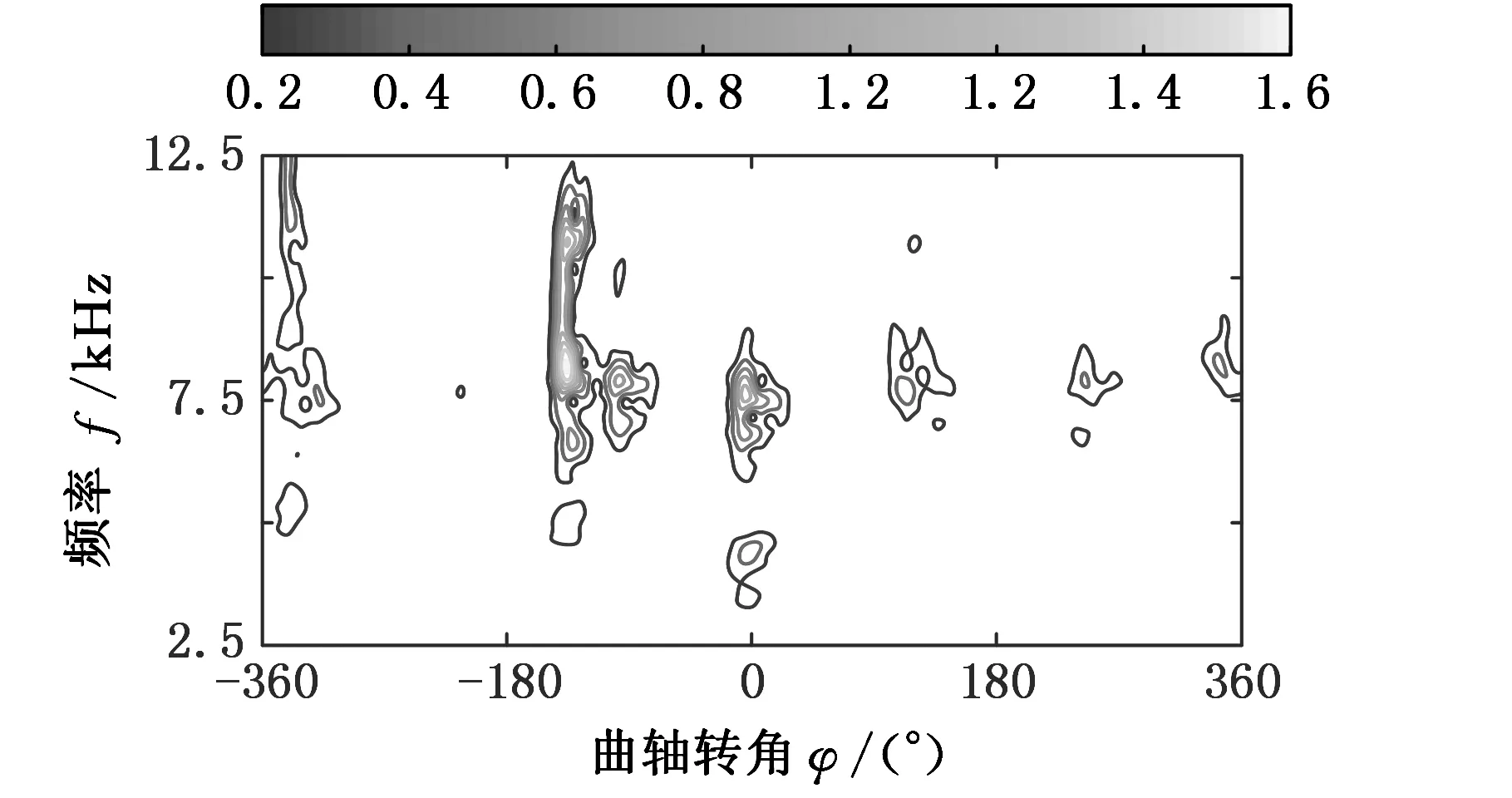
(a)振动谱

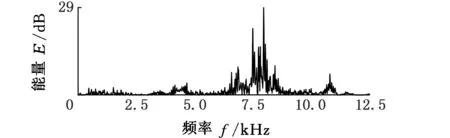
(b)功率谱

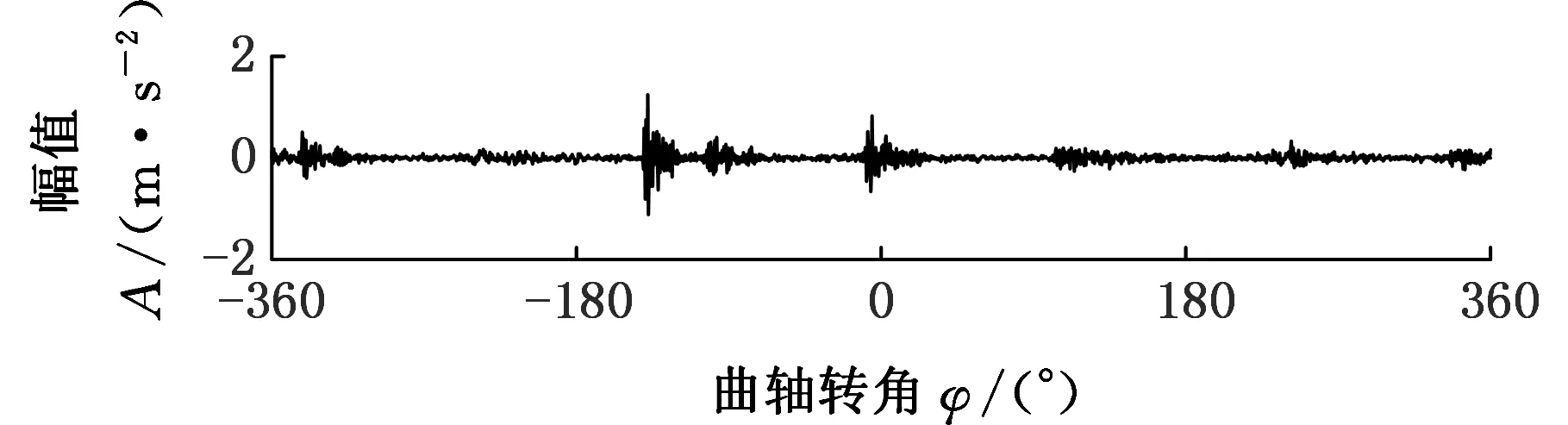
(c)时域波形图3 振动信号的离散广义S变换Fig.3 Discrete Generalized S-transform of Vibration Signals

由图3可以看出，信号的时频相平面(等高线图)具有对信号的局部定位功能。气体燃烧效率和进、排气门开启和关闭作用的时间，均可在图像中反映出来，且正常状态下，振动信号的频率多集中于高频(5～12 kHz)。

不同工况下，缸盖表面的振动信号的频率分量有所不同，因此要结合实际情况，适当调整参数大小，从而在信号分解过程中使“基函数”与振动信号达到更好的匹配。表2参数设置下的时频表征如图4所示。

表2 不同工况下的参数取值

从工况2、4、5可知，由于漏气的影响，混合气体的燃烧功率得到不同程度的下降。工况6中，当进、排气门间隙均小时，对气体燃烧激励的影响最大。对于工况3、7和8，当排气门间隙过大时，排气门开启迟后，缩短排气时间，从而改变了正常的配气相位，造成功率下降。通过以上分析可知，不同进、排气门间隙的情况下，气门落座冲击和混合气体的燃烧效率不同，因此利用振动谱图像对气阀状态进行分类识别是切实可行的。

(a)工况1

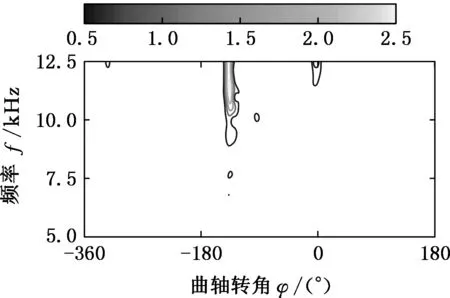
(b)工况2

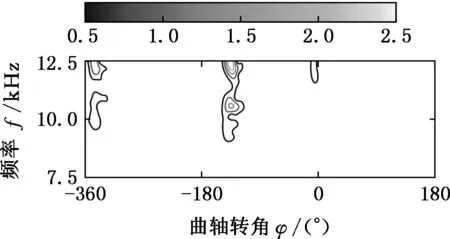
(c)工况3

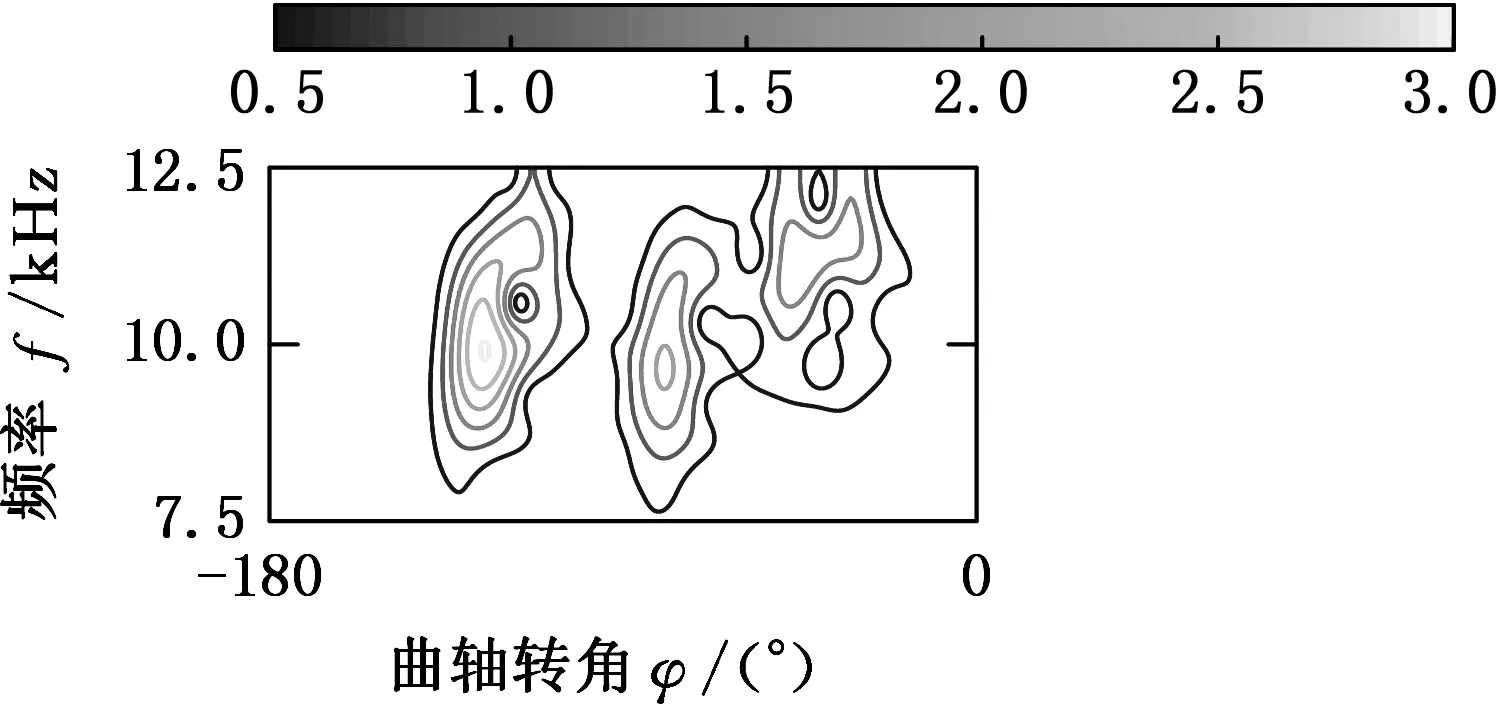
(d)工况4

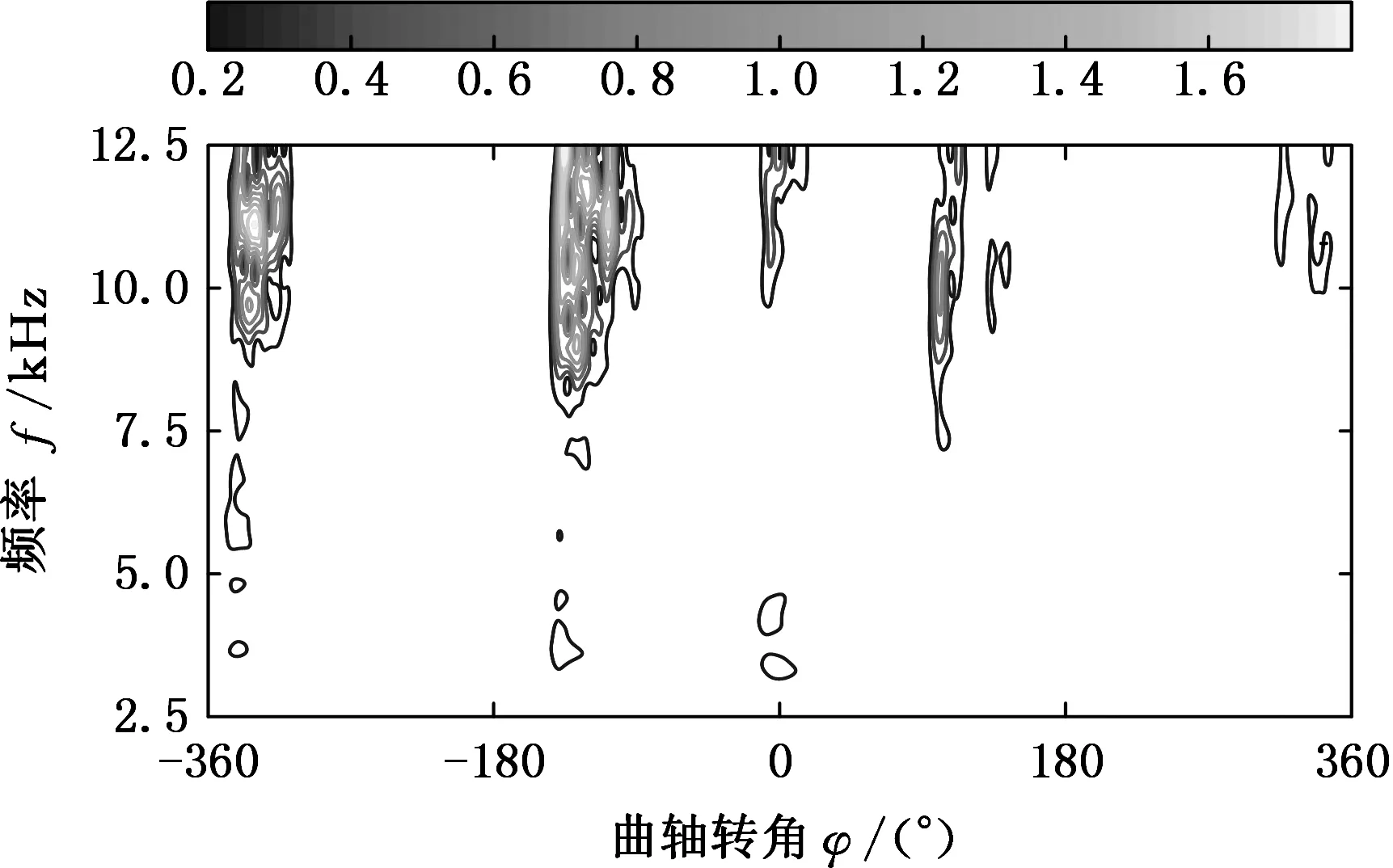
(e)工况5

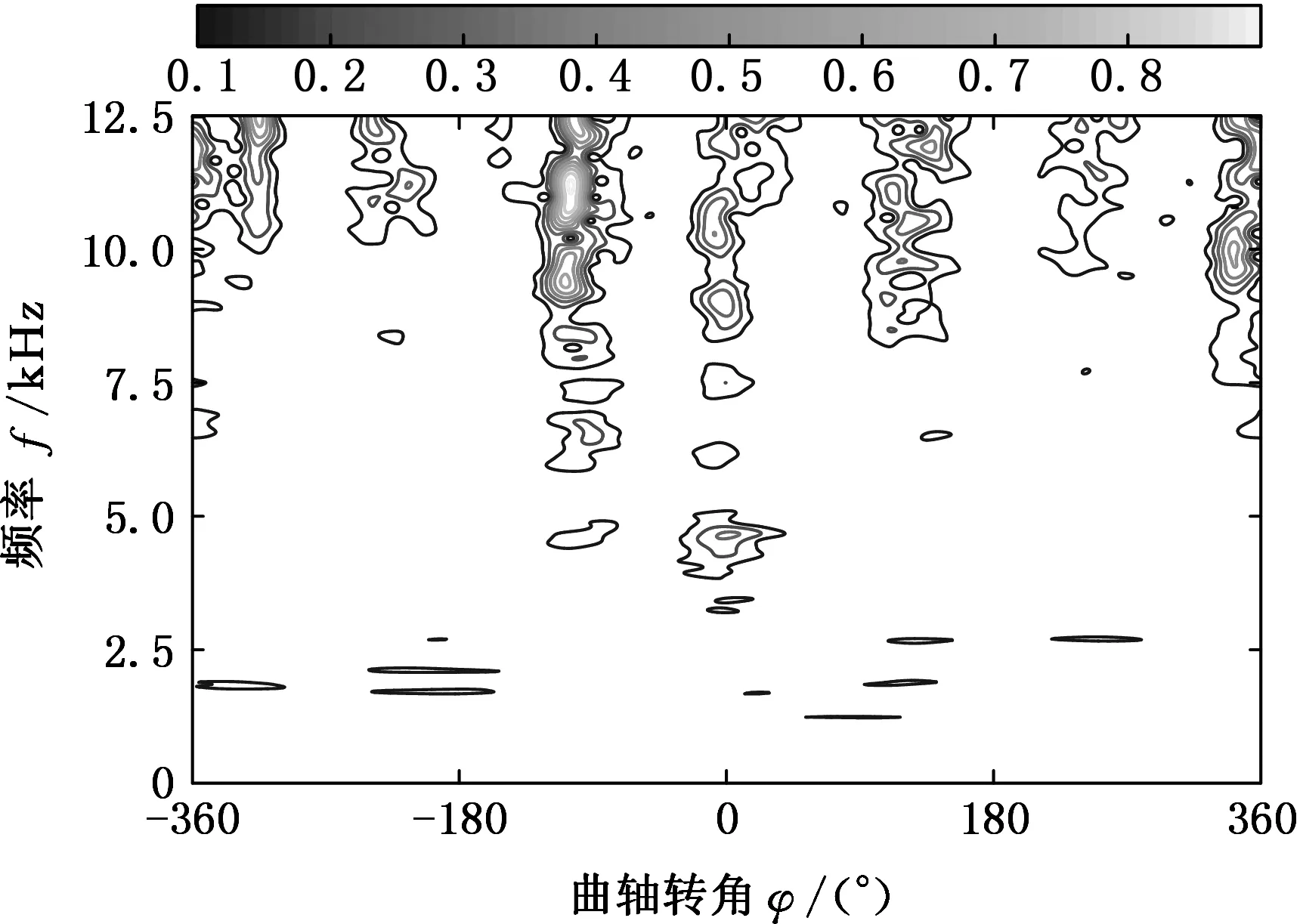
(f)工况6

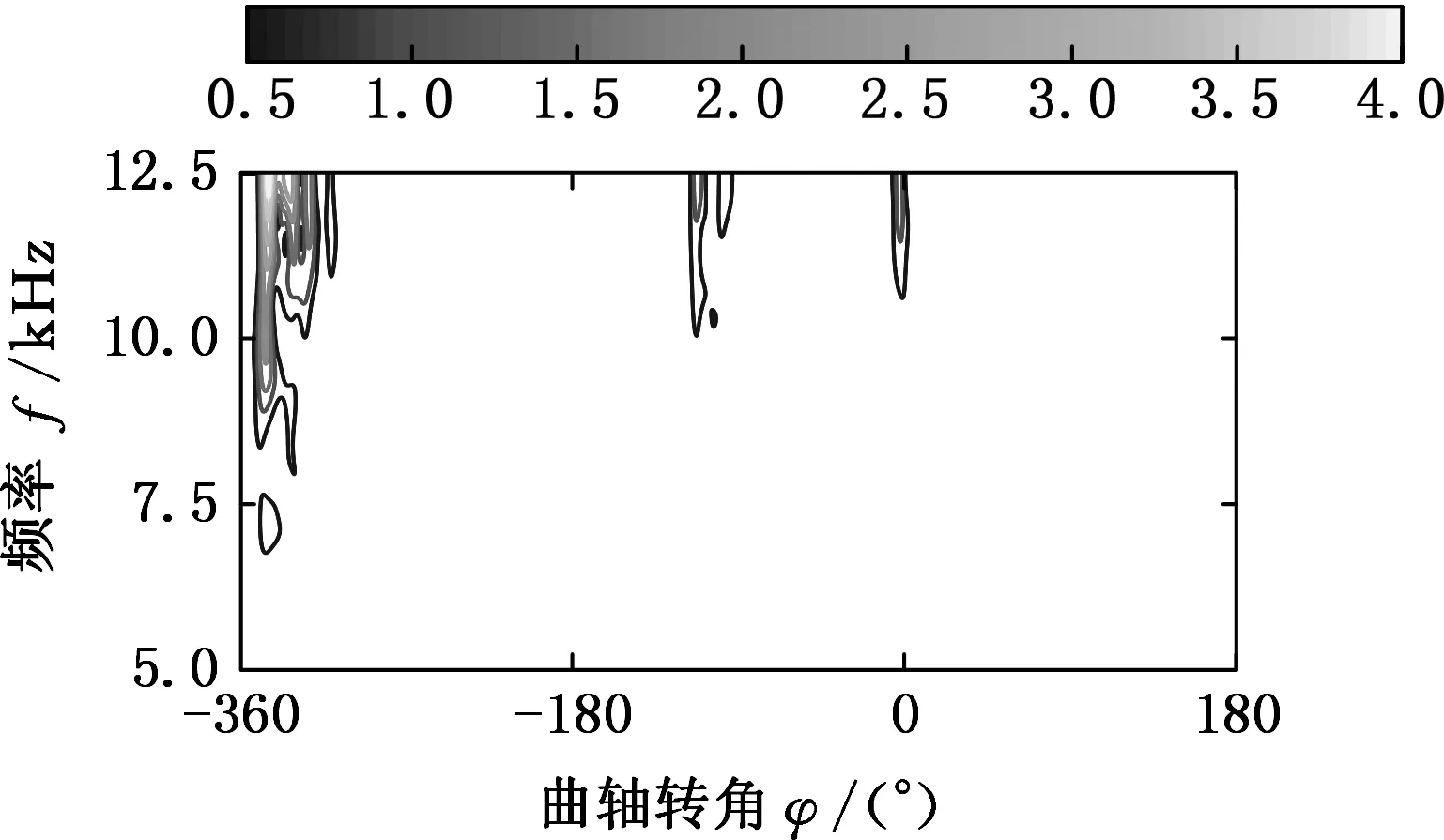
(g)工况7

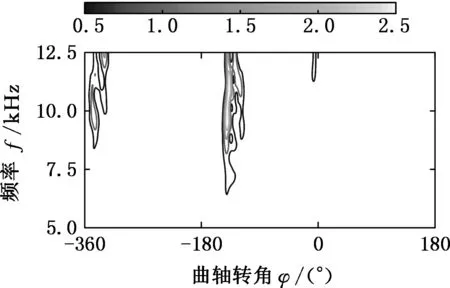
(h)工况8

2.3 离散广义S变换时频图像特征提取

对于特征提取来讲，随着图像处理个数的增加，特征系数所占用的存储空间逐步增大，计算效率逐步降低。为突出本文所提方法的实用性，在图像处理个数相同的情况下，分别采用模块二维主成分分析(M-2DPCA)、二维线性判别分析(2DLDA)、2DPCA以及TD-2DPCA对图像进行特征提取，并对比计算效率，结果如表3所示。由于前三种方法只能对图像进行单向压缩，所以在计算效率的对比方面只对比单方向上图像特征维数相同时的耗用时间，即d=(4，5，6，7，8，9)。同样，M-2DPCA特征提取时，每个样本图像分成4×4块，且设定子图像的特征维数与其他方法的特征维数相同。

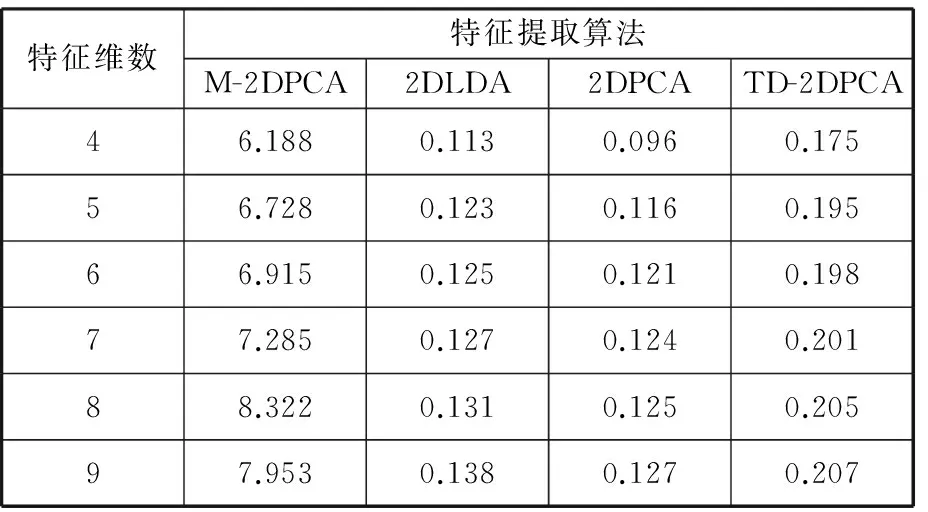
表3 不同特征提取方法的计算效率

由表3得知，随着维数的增加，4种特征提取方法的计算时间均会延长。M-2DPCA特征提取方法需要对图像进行分块处理，然后利用所有子图像计算最优投影矩阵，特征系数矩阵类间散度得以提升但计算效率下降严重。TD-2DPCA、2DPCA以及2DLDA在计算效率上有了极大的提高，相比之下TD-2DPCA特征提取中增加了图像纵向压缩环节，计算时间稍长于另外两种方法，但依然表现出良好的适用性。

经TD-2DPCA特征提取后的图像，大小由84×112变为h×d，在保留图像主要信息的基础上极大地减小了图像维数。图5给出的是h×d=10×10时，离散广义S变换时频表征的特征系数矩阵，图像中每个像素的灰度严格与样本系数值一一对应。此处只选前4种工况，每种工况取5个样本来说明问题。

由图5可得，同类样本间的相似性和不同类样本的差异性比较明显，且图的左上角集中反映特征编码值的大小。这是因为对图像进行特征提取时，首先进行横向压缩，提取的第一主分量位于第一列，其次进行纵向压缩，提取的前两个主成分位于前两行。类内相似和类间差异为设备运行状态的模式识别提供了有力支撑。

2.4 分类识别

最近邻分类器通过比较未知样本与已知样本间的欧氏距离，从而决定其从属类型[14]。本文采用最近邻分类器检验4种特征提取方法的适用性，并对比标准S变换、离散广义S变换两种时频表征方法的识别结果，以说明离散广义S变换的优越性。

实验中，每种工况各60幅图像，8种工况共480幅。取各工况任意30幅图像，共240幅组成训练样本，其余240幅组成测试样本。同种诊断方法的测试结果重复10次取平均值，作为最终识别率，结果如图6、图7所示。

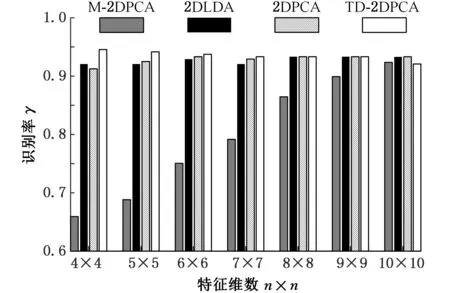
图6 标准S变换振动谱图识别精度Fig.6 Recognition accuracy of standard S-transform

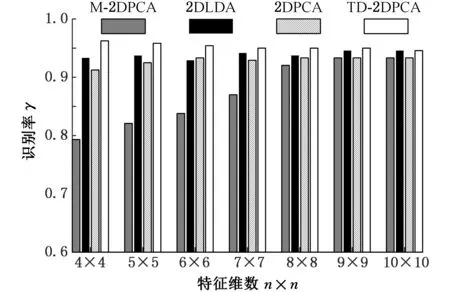
图7 离散广义S变换振动谱图识别精度Fig.7 Recognition accuracy of discrete generalized S-transform

由图7可知，当特征维数较小时，M-2DPCA特征提取方法识别率较低，但随着特征维数的增加，识别率逐步提高；其余3种特征提取方法受特征维数的影响较小，TD-2DPCA特征提取方法识别率相对较高。对比图6、图7可知，离散广义S变换提高了时频表征的聚集性，4种特征提取方法的识别精度均有大幅提高，其中，M-2DPCA提取方法的识别精度提高最为明显，然而依旧低于其他三种方法。此时，在低维特征空间中，TD-2DPCA最高识别率可达到96.25%，高于文献[15]中采用时序分析与神经网络模拟其中5种工况的平均识别率92.2%。同时，当训练样本所占全部样本的比例等同于文献[16]中的比例时，针对模拟的相同的8种工况，本文方法的识别率也高于文献[16]的识别率95%。从文中的对比分析可知，离散广义S变换时频表征优于标准S变换，同时TD-2DPCA特征提取在计算效率和识别精度上均体现出较好性能。

3 结论

(1)离散广义S变换可根据内燃机振动信号的不同特点，调节窗函数中参数大小使“基函数”与信号实现更好的匹配，从而有效提高时频图像聚集性，并在离散化处理的过程中减少信息冗余，降低了运算复杂度。

(2)TD-2DPCA在2DPCA的基础上对图像进行纵向压缩，在保证识别精度的同时极大缩减了特征系数矩阵的维数，且此特征系数矩阵能保证同类样本相似、不同样本差异的特性。

(3)将离散广义S变换与TD-2DPCA的诊断方法用于内燃机气阀机构的故障诊断，实验结果表明该方法在计算效率与识别精度方面都具有良好的诊断性能，体现出实用性。

另外，在窗口调节的过程中受到启发，不同的参数设置方式对窗函数变化有较大影响，针对不同的时频图像寻找更优良的窗函数模型将是下一步研究的方向。

参考文献：

[1] 胡振邦,许睦旬,姜歌东,等.基于小波降噪和短时傅里叶变换的主轴突加不平衡非平稳信号分析[J].振动与冲击, 2014, 33(5):20-24.

HU Zhenbang, XU Muxun, JIANG Gedong, et al. Analysis of Unbalanced Non-stationary Signal of Spindle Based on Wavelet Denoising and Short-time Fourier Transform[J]. Vibration and Shock, 2014, 33(5):20-24.

[2] 岳应娟,孙刚,蔡艳平.基于小波包振动谱图的柴油机在线故障诊断方法[J].舰船科学与技术, 2016, 38(8):128-133.

YUE Yingjuan, SUN Gang, CAI Yanping. On-line Fault Diagnosis Method of Diesel Engine Based on Wavelet Packet Vibration Spectrum[J]. Ship Science and Technology, 2016, 38(8):128-133.

[3] 蔡艳平,李艾华,石林锁,等. 基于EMD-WVD振动谱时频图像SVM识别的内燃机故障诊断[J].内燃机工程, 2012, 33(2): 72-79.

CAI Yanping, LI Aihua, SHI Linsuo, et al. Fault Diagnosis of Internal Combustion Engine Based on EMD-WVD Vibration Spectrum Time-frequency Image SVM Recognition[J]. Internal Combustion Engine Engineering, 2012,33(2):72-79.

[4] 李志农,朱明,龙盛蓉.新非平稳信号处理方法——自适应径向墨西哥草帽核时频分布[J].振动与冲击, 2015, 34(10): 184-190.

LI Zhinong, ZHU Ming, LONG Shengrong. New Non-stationary Signal Processing Method—Adaptive Radial Mexican Straw Kernel Time-frequency Distribution[J]. Vibration and Shock, 2015, 34(10):184-190.

[5] STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the Complex Spectrum: the S Transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.

[7] 郭远晶,魏燕定,周晓军,等. S变换用于滚动轴承故障信号冲击特征提取[J]. 振动、测试与诊断, 2014, 34(5): 818-822.

GUO Yuanjing, WEI Yanding, ZHOU Xiaojun, et al. S-transform is Used to Extract the Impact Characteristics of Rolling Bearing Fault Signal[J]. Vibration, Testing and Diagnosis, 2014, 34(5): 818-822.

[8] 胡广书.现代信号处理教程[M]. 2版.北京：清华大学出版社, 2015.

HU Guangshu. Modern Signal Processing Tutorial[M]. 2nd ed. Beijing: Tsinghua University Press,2015.

[9] LIU K, CHENG Y Q, YANG J Y. Algebraic Feature Extraction for Image Recognition Based on an Optimal Discriminant Criterion[J]. Pattern Recognition, 1993, 26(6): 903-911.

[10] YANG J, ZHANG D, FRANGI A F, et al. Two-dimensional PCA: a New Approach to Appearance-based Face Representation and Recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137.

[11] 陈伏兵,陈秀宏,张生亮,等.基于模块2DPCA的人脸识别方法[J]. 中国图象图形学报, 2006, 11(4): 580-585.

CHEN Fubing, CHEN Xiuhong, ZHANG Shengliang, et al. Face Recognition Method Based on Module 2DPCA[J]. Journal of Image and Graphics, 2006, 11(4): 580-585.

[12] 李巍华,林龙,单外平.基于广义S变换与双向2DPCA的轴承故障诊断[J]. 振动、测试与诊断, 2015, 35(3): 499-506.

LI Weihua, LIN Long, SHAN Waiping. Bearing Fault Diagnosis Based on Generalized S-Transform and Bidirectional Principal Components Analysis[J]. Vibration, Testing and Diagnosis, 2015, 35(3): 499-506.

[13] LI M, YUAN B. 2D-LDA: a Statistical Linear Discriminant Analysis for Image Matrix[J]. Pattern Recognition Letters, 2005, 26(5): 527-532.

[14] 许国根,贾瑛.模式识别与智能计算的MATLAB实现[M]. 北京：北京航空航天大学出版社, 2012.

XU Guogen, JIA Ying. Realization of Pattern Recognition and Intelligent Computing[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2012.

[15] 夏勇,商斌梁,张振仁,等.基于时序分析与神经网络的气阀机构故障诊断[J]. 机械设计与研究, 2001,17(1):71-74.

XIA Yong, SHANG Binliang, ZHANG Zhenren, et al. Fault Diagnosis of Valve Mechanism Based on Time Series Analysis and Neural Network[J]. Mechanical Design and Research, 2001,17(1):71-74.

[16] 王成栋,魏瑞轩,张优云,等.模糊函数图像与概率网络在柴油机气阀故障诊断中的应用[J]. 内燃机工程, 2004, 25(5): 19-23.

WANG Chengdong, WEI Ruixuan, ZHANG Youyun, et al. Application of Fuzzy Function Iimage and Probabilistic Network in Diesel Engine Valve Fault Diagnosis[J]. Internal Combustion Engine Engineering, 2004, 25(5): 19-23.