指数和高斯随机粗糙表面光散射特性数值研究∗

闫克丁 付永升 于小宁 杨建华

（西安工业大学 西安 710021）

1 引言

粗糙表面光散射是一个长期保持吸引力的研究领域，现代科技中许多技术以此为基础，比如雷达，随着纳米技术的进步，根据光散射理论来设计具有特定表面光学散射特性的新材料，比如超材料、光子晶体、光时钟、可设计表面等。第一位理论研究表面散射的学者是Lord Rayleigh，他在19世纪末开始系统研究粗糙表面的波散射而难题，研究了光垂直入射到正弦表面的散射现象［1］，1913年Mandel'shtam［2］第一个考虑到随机粗糙表面散射，开创了一个新的研究领域：随机粗糙表面的波散射，他主要研究了液体表面的光散射。近年来一些随机表面光散射的新现象被理论预测和实验验证，如多次散射，增强后向散射，卫星峰现象等［3～5］。目前广泛使用的随机粗糙表面光散数值计算仿真方法有电磁场数值方法包括有限元法（FEM）、时域有限差分法（FDTD）和矩量法（MOM）等方法［6～8］。FEM和FDTD数值计算需要对整个仿真域进行离散，MOM则只需对粗糙表面进行离散，是一种有效研究这类粗糙面散射问题的方法及工具。

在目前随机粗糙表面的光散射研究中时，大部分的文献采用的是高斯分布随机粗糙表面，而对指数分布随机粗糙表面的散射特性研究较少，指数分布随机粗糙表面适用于描述具有尖峰的不规则表面，通过对指数分布随机粗糙表面的光散射性质的研究，可以帮助我们了解这类表面的光学性质。因此本文生成采用线性滤波法分别生成高斯分布和指数分布的随机粗糙表面，采用矩量法数值计算两类随机表面的平均差分散射系数，对比两类表面的光散射特性。

2 随机粗糙表面

一般可认为随机粗糙表面高度可由许多不同频率的谐波叠加而成，因此可采用线性滤波法来生成随机粗糙面：先进行频域滤波，然后进行逆傅里叶变换得到粗糙面高度，来生成模拟随机粗糙面模型［9～10］。根据以上分析，长度为 L 的一维粗糙面模型可表示为

3 锥形入射波

随机表面光散射计算时，需要计算无限大表面，但数值计算只能针对有限尺寸的表面，因此必须对表面截断。当 ||x，y＞L时，表面电流密度为0，在表面的边界会产生电流密度的突变。通常有两种方法处理电流密度突变：设置周期边界和锥形入射波。设置周期边界方法会产生近似，引入误差，一般较少使用；锥形入射波具有Gauss特性，入射波在边界时衰减到0，这样可避免表面电流密度的突变。

一维锥形入射波公式：

入射波波矢为

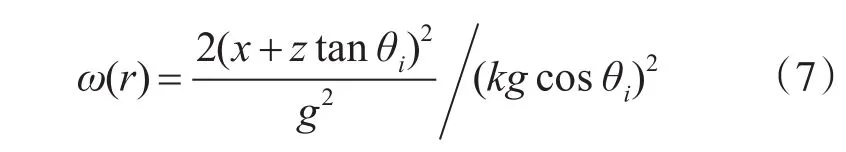
其中，g为锥形宽度，一般选择在L 4和L 10之间，决定入射波宽度和随机粗糙表面尺寸，g越大，入射波宽度越大，粗糙表面尺寸越大，计算结果更精确，但计算强度增加，计算时间加大，因此必须选择合适的g值，锥形宽度由入射角决定，随机粗糙表面的长度L由g决定。

根据上式可得一维锥形入射波的振幅分布如图1所示。

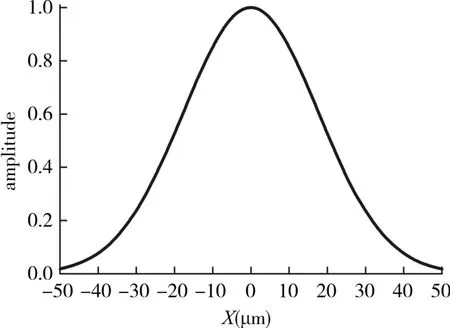
图1 一维锥形入射波的振幅分布

4 基于MOM粗糙表面散射计算方法

一维随机粗糙表面散射示意图如图2所示，θi为入射角，θs为散射角，ki为入射光波矢，ks为散射光波矢。

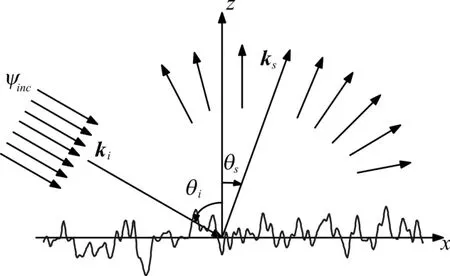
图2 一维随机粗糙表面散射结构示意图

对于良导体随机粗糙表面光散射，总场等于入射场与散射场之和：

利用格林函数可得

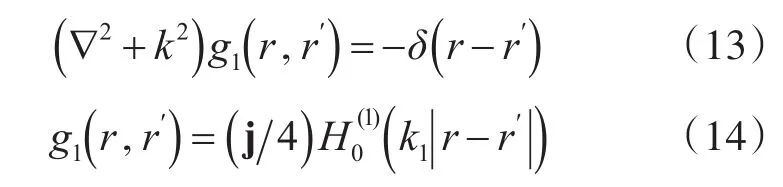
应用格林第二恒等式，化简可得到

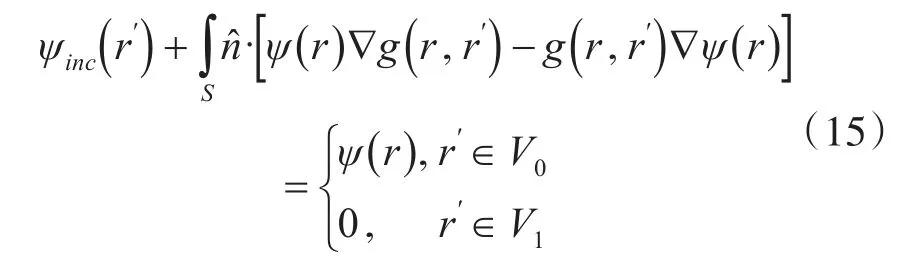
r在粗糙表面，r′在粗糙面上V0或下V1。

由于光波照射在电介质表面上会产生电流和磁流，因此必须建立电磁场双积分方程：

根据边界条件：

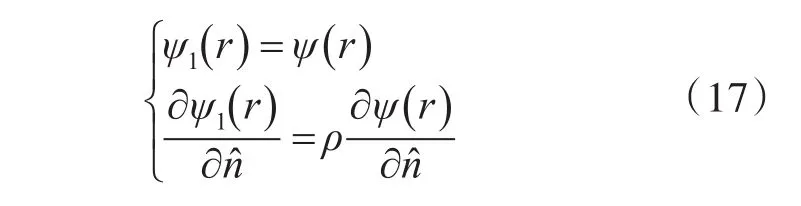
其中当入射光为S偏振光时，ρ为μ1μ，入射光为P偏振光时ρ为ε1ε，将边界条件带入节分方程得

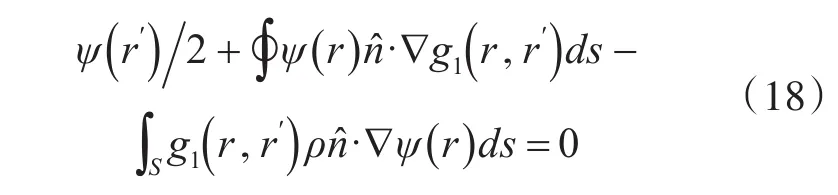
对于金属表面和电介质表面散射得到的积分方程（15）和（18）采用点配法得到矩阵方程，采用Bi-CGSTAB算法求解矩阵方程，最后得到散射场ψ(r′)S

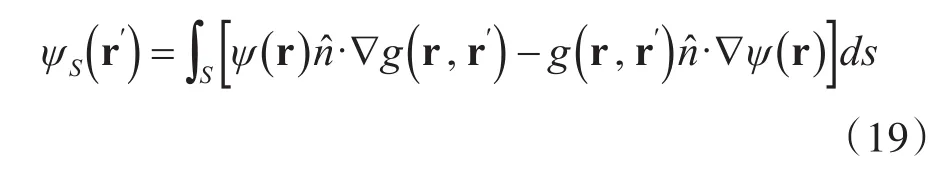
当 r′在远场时，散射场波矢=sinθS+cosθS，g(r ， r′)为格林函数为

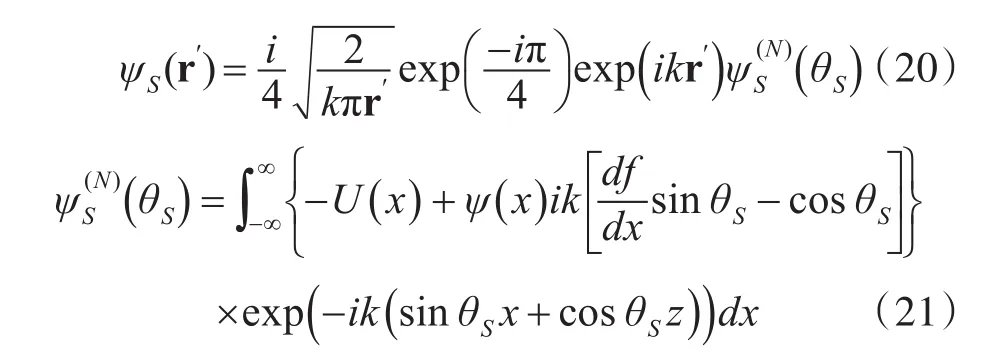
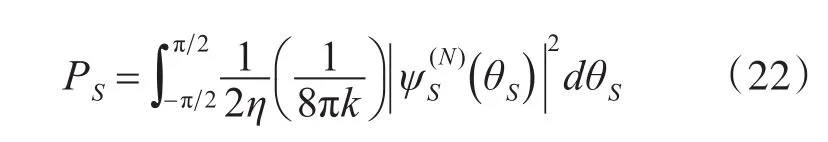
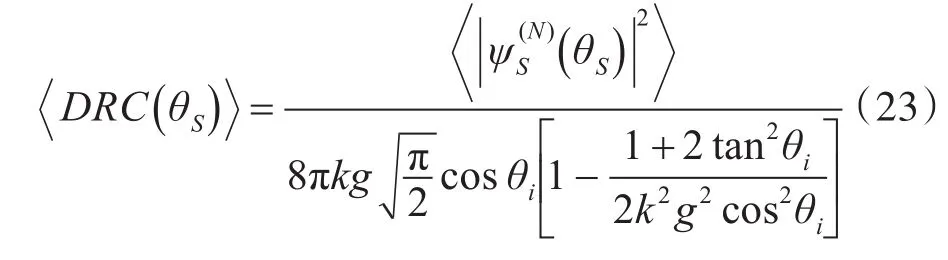
5 结果与讨论

光散射特性进行数值研究选择入射光波长λ=1.064μm，每个参数的计算分别产生10000个样本表面，每个样本长度为100λ，数值计算采样点数为N=2048。选择一组表面，表面粗糙度参数如表1所示，这些表面属于常见的微粗糙和弱粗糙表面。

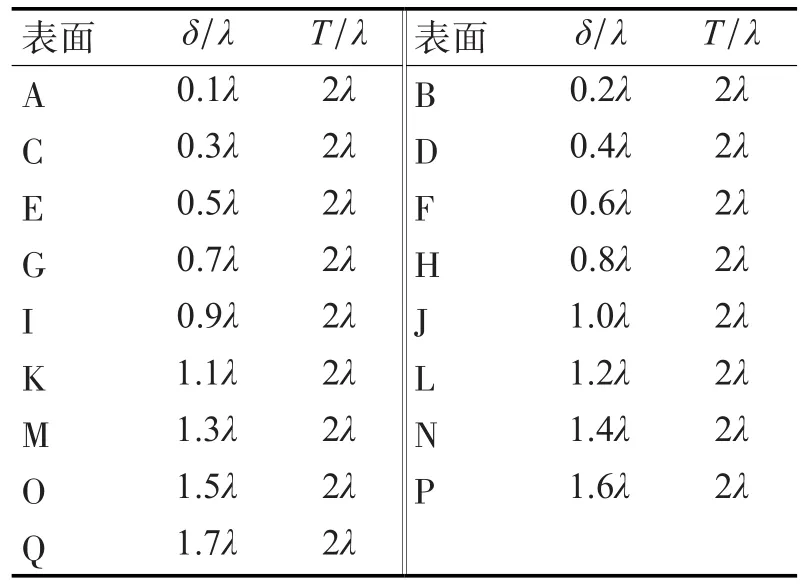
表1 粗糙表面样本粗糙度参数

高斯分布随机粗糙良导体表面在30°入射角情况下散射结果结果图3所示。

对良导体随机粗糙表面光散射MDRC分布特性用分布宽度、散射峰值、峰位置三个参量表示。

从图3中可以看到高斯分布随机粗糙表面散射特性，T=2λ固定不变，当 δ=0.1λ时，如图3（a）中出现镜像散射峰，S入射光与P入射光散射分布相似，镜像峰值随着入射角的增大而增大；随着δ的增大，散射强度分布变宽，出现类似朗伯体漫反射现象，散射强度分布变宽，因此在T固定时，δ会有一个朗伯散射区间出现，朗伯散射强度随着入射角度的增大而增大，但增幅不大，并且散射峰值向大散射角方向移动，此时S入射光比P入射光散射峰值要大一些；随着δ的进一步增大，δ=0.8λ时S入射光散射出现后向增强峰值，P光则没有，后向增强峰值在θi＜20°时比较明显，并且随入射角增大，后向增强峰值变小，对比图3（K）（L）（M）可发现随粗糙度增大，后向散射峰值变大。

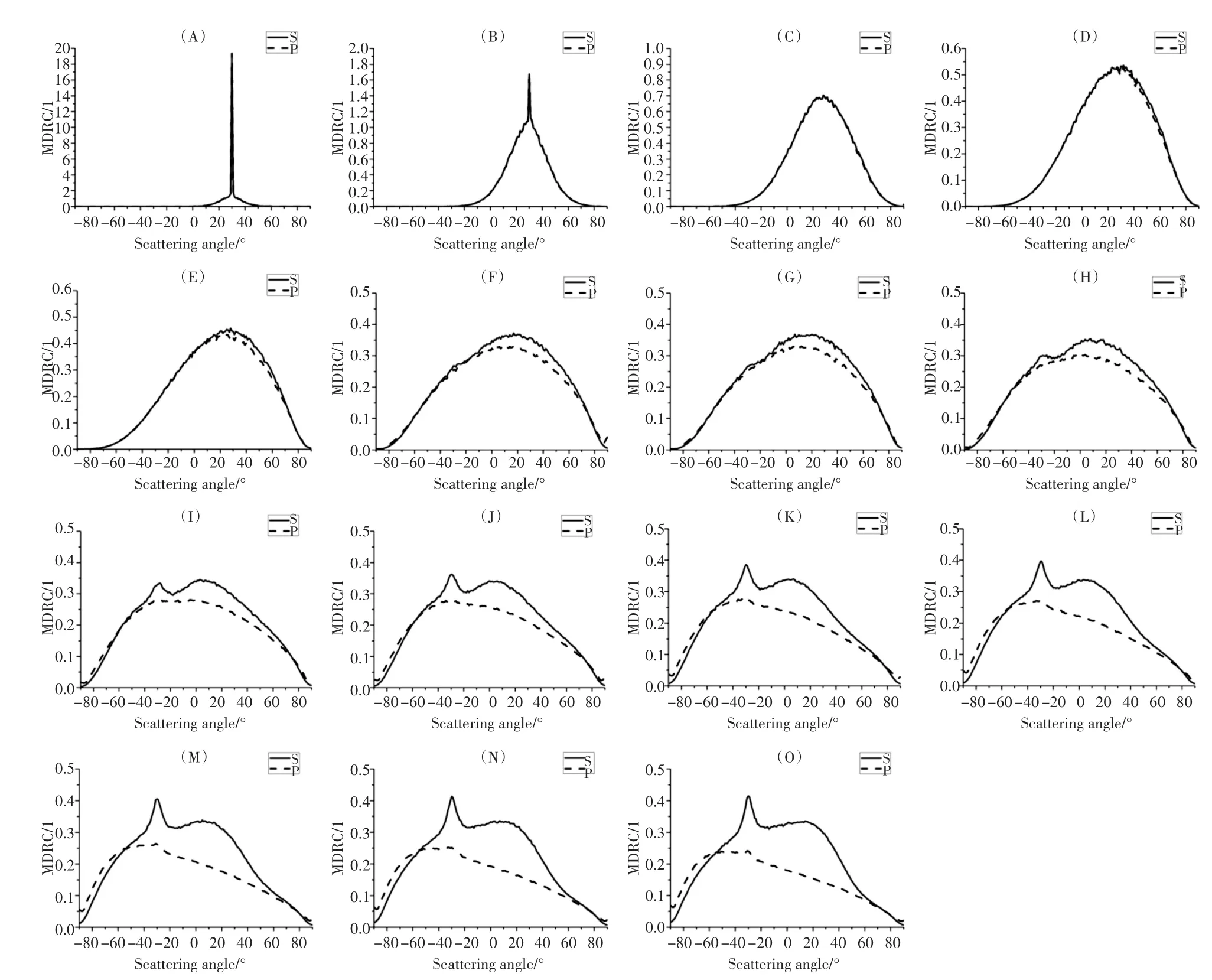
图3 高斯分布随机粗糙表面光散射MDRC分布

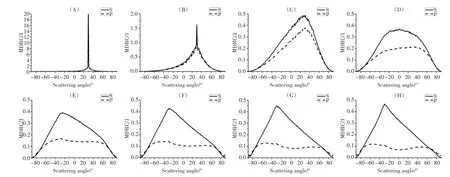
图4 指数分布随机粗糙表面光散射MDRC分布

从图4中可得到指数分布随机粗糙表面散射特征：δ=0.1λ时，指数分布粗糙表面具有与高斯分布粗糙表面相似的散射特征，散射光强相近。δ=0.2λ时，指数分布粗糙表面与高斯分布粗糙表面散射光有相同的峰值，但是散射光强分布曲线有差异，指数分布粗糙表面散射分布曲线具有指数增长和下降趋势，而高斯粗糙表面的散射分布对称。δ=0.3λ时，指数分布粗糙表面散射峰值与δ=0.4λ的高斯分布粗糙表面散射峰值相同，但散射分布有差异，高斯分布粗糙表面散射分布比较光滑，而指数分布粗糙表面散射分布比较尖锐。当δ=0.4λ时，指数分布粗糙表面的散射峰值与δ=1λ的高斯分布粗糙表面散射峰值相同，指数分布粗糙表面散射为朗伯散射，散射宽度比指数分布粗糙表面散射宽度更宽。随着方均根高度进一步增大，当δ=0.5λ和δ=0.6λ时，指数分布粗糙表面散射分布出现后向峰值，并且分布曲线以接近直线的形式向峰值两端下降。经指数分布随机粗糙表面与高斯分布粗糙表面散射光特性对比可知，具有相同粗糙参数情况下，指数分布随机粗糙表面比高斯分布粗糙表面显得更为粗糙。

为了更好地对比指数分布粗糙表面和高斯分布粗糙表面的散射特征，设定一组粗糙表面参数：粗糙面方均根高度为δ=0.5λ，相关长度为T=4λ，采样点数N=2048，粗糙面长度L=100λ。使用该组粗糙参数分别生成指数分布表面和高斯分布表面两种表面，如图5所示。

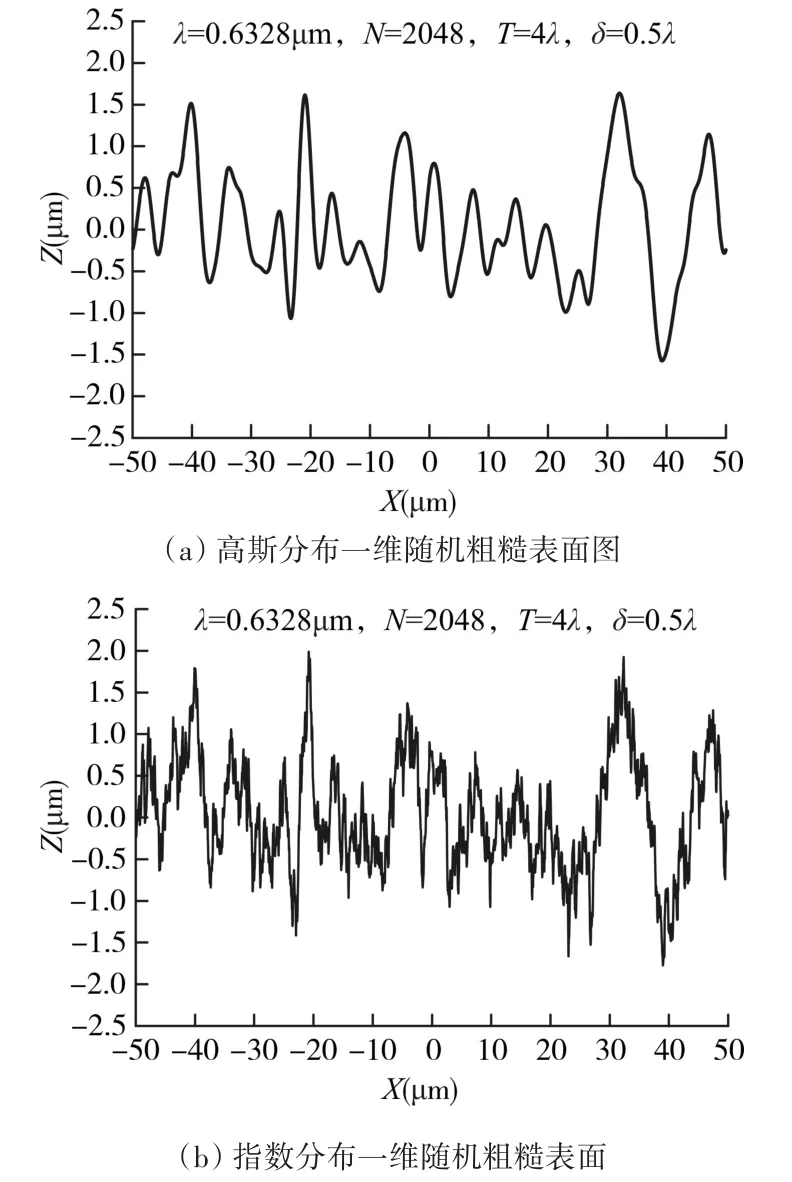
图5 高斯分布与指数分布一维随机粗糙表面

从图5中可看出，相同随机数生成的高斯分布和指数分布随机粗糙表面之间有相似的起伏变化趋势，但高斯表面比较光滑，指数表面相比于高斯表面具有更多毛刺，因而比高斯分布粗糙表面更加粗糙，从而造成了上述指数分布表面和高斯分布散射结果的差异。

6 结语

本文研究了高斯分布和指数分布随机粗糙表面的光散射分布特性，采用线性滤波法生成一组高斯分布和一组指数分布随机粗糙表面，采用基于矩量法的蒙特卡罗算法分别计算了指数分布和高斯分布表面的散射光强度平均差分散射系数MDRC，分析了MDRC分布、散射峰值、散射峰位置等特征。数值计算结果显示高斯分布和指数分布随机粗糙面的散射特征具有显著差异，研究结果对复杂背景下提高激光雷达目标识别能力具有重要意义。

［1］Rayleigh L.On the dynamical theory of gratings［J］.Pro⁃ceedings of the Royal Society of London.Series A，Con⁃taining Papers of a Mathematical and Physical Character，1907，79（532）：399-416.

［2］Landsherg G S，Mandelstam L I.New phenomenon in scat⁃tering of light（preliminary report）.Journal of the Russian Physico-Chemical Society，1928，Physics Section 60，335-336.

［3］Letnes P A，Maradudin A A，Nordam T，et al.Calcula⁃tion of the Mueller matrix for scattering of light from two-dimensional rough surfaces［J］.Physical Review A，2012，86（3）：031803.

［4］Simonsen I，Maradudin A A.Numerical simulation of elec⁃tromagnetic wave scattering from planar dielectric films de⁃posited on rough perfectly conducting substrates［J］.Op⁃tics communications，1999，162（1）：99-111.

［5］O'Donnell K A，Méndez E R.Enhanced specular peaks in diffuse light scattering from weakly rough metal surfaces［J］.JOSA A，2003，20（12）：2338-2346.

［6］Harvey J E，Krywonos A，Vernold C L.Modified Beck⁃mann-Kirchhoff scattering model for rough surfaces with large incident and scattering angles［J］.Optical Engineer⁃ing，2007，46（7）：078002.

［7］Simonsen I，Vandembroucq D，Roux S.Electromagnetic wave scattering from conducting self-affine surfaces：an analytic and numerical study［J］.JOSA A，2001，18（5）：1101-1111.

［8］Bruce N C，Dainty J C.Multiple scattering from random rough surfaces using the Kirchhoff approximation［J］.Jour⁃nal of modern optics，1991，38（3）：579-590.

［9］Hu Y.Z.and Tonder K.Simulation of 3-D random rough surface by 2-D digital filter and fourier analysis.Interna⁃tional Journal of Machine Tools and Manufacture，1992，32（12）：83-90.

［10］Patir，N.，A numerical procedure for random generation of rough surfaces.Wear，1978.47（2）：263-277.