最值问题简解探源

江苏省如皋中学

孙心怡 范栋志 (邮编：226500)

1 试题呈现 答案比较

(2016-2017江苏省苏北四市高三联考试卷第14题)已知函数f(x)=|x2-4|+a|x-2|x∈[-3,3].若f(x)的最大值是0，则实数a的取值范围是______.

参考答案1因为函数f(x)的最大值为0，故函数f(x)≤0在[-3，3]上恒成立，从而f(3)≤0⟹a≤-5.

又f(x)=

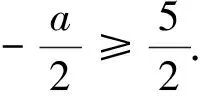
参考答案2因为f(x)=|x-2|(|x+2+a),|x-2|≥0,且函数f(x)的最大值为0，故|x+2|+a≤0在[-3，3]上恒成立，从而a≤-|x+2|在[-3，3]上恒成立.因为-|x+2|的最小值为-5，故a≤-5.

2 解法探究 寻根概念

显然，参考答案2比参考答案1简单，为什么函数的最大值可以转化为恒成立问题？会不会出现范围扩大的问题？是不是所有的最值问题都可以转化为恒成立问题？高兴之余，还要寻找支撑这种方法的理论根据，只有有据可依，才能在解题时灵活应用.俗话说：一切方法的源头在于概念，理解概念的内涵与外延是解题的基础.下面尝试着从最值的概念上寻找答案(苏教版必修1).

对最值概念理解如下：

(1) 函数的最大(最小)值就是函数值域中的最大(最小)的元素.(直观感知)

(2) 从图象上理解：函数的最大(最小)值就是函数图象最高(最低)点的纵坐标.

(3)最值定义中的(1)是不等式恒成立，(2)说明最值是函数值，必须要有自变量与之对应，这样等号才能取到.

(4)函数y=f(x)取得最大值(最小值)m时，其图象都不在直线y=m的上方(下方)，且与直线y=m有交点.

上述试题中f(x)=|x2-4|+a|x-2|，x∈[-3,3]中f(2)=0一定成立，由上述最值概念理解(3)可知，已满足第(2)个条件，只需要满足第(1)个条件，即f(x)=|x2-4|+a|x-2|≤0在x∈[-3,3]上恒成立.

定义是充要条件，所以其逆命题也是正确的.设函数y=f(x)的定义域为I，m是函数y=f(x)的最小值(最大值)，则(1)对于任意的x∈I，都有f(x)≥m(f(x)≤m)；(2)存在x0∈I，使得f(x0)=m.

据此可知参考答案2的解法不仅不会出现范围扩大，而且起到了化繁为简的作用，的确是一种好方法.

兴奋之余期待大展身手.翻开笔记一道试题映入眼帘.

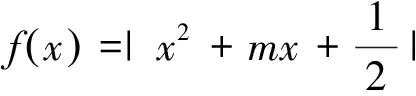
回忆之前解决这道题的过程，利用图象讨论了二次函数对称轴与区间的三种位置关系，还要研究在区间内函数值的正负，层次多，分类杂.上述解法层次清楚，简单明了，极大简化了过程和运算.

3 疑窦丛生 深度理解

惊叹上述解法的同时，极力寻找更多的用武之地，期待得到再次证明.翻开笔记、错题集，试题集，发现函数最值的试题很多，但完全满足上述条件的试题少之又少，难道这种方法不具有普遍性，不是通性通法？放弃研究还是继续前行，我徘徊在十字路口.“最值概念由理解(3)中(1)(2)共同决定，只要保证同时满足(1)(2)就行了”，老师的及时点拨拨开了思维的迷雾，让我顿悟了一般试题与上述试题的本质区别，上述两道试题均已恒满足条件(1)，但绝大多数试题两个条件均不恒满足.下面借助一道试题来小试牛刀.

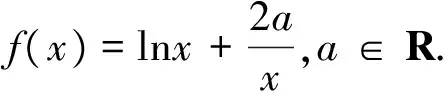
分析由题意可知f(x)应满足条件(2)即f(x)≥3在[1,e]上恒成立，化简可得2a≥3x-xlnx.因为(3x-xlnx)′=2-lnx>0，所以函数3x-xlnx在[1,e]上单调递增，可得3x-xlnx的最大值为2e，推出a≥e.

要使得函数f(x)上的最小值为3，还必须满足条件(1)，即等号能够取到，有自变量与之对应.可转化为不等式2a≥3x-xlnx中等号能够取到，由于3x-xlnx≤e，当a>e时，直线y=a与函数y=3x-xlnx无交点，不存在自变量与之对应.当a=e时，直线y=a与函数y=3x-xlnx有唯一交点(e,e)，存在自变量x=e与之对应.

结合函数最值的定义，可知a=e.

类比上述解法发现“已知函数在某区间的最值，求参数的取值”此类问题可以先从条件(2)出发，将最值问题转化为恒成立问题，通过分离参数的方法，计算出参数的取值范围.再利用条件(1)去伪存真.类比上述发现其实参数的取值就是其范围的边界值.恒成立问题在高中数学中较为常见,其解决的途径有很多.将最值问题转化为恒成立问题来处理，拓宽了最值问题解决的渠道.

数学学习痛并快乐着，其中有惊喜，有烦恼，更有对意志力的考验，那种大彻大悟后的酣畅淋漓值得久久回味，我愿意在数学学习的道路上不断前行，深度思考，享受数学的美与妙.