立足课本 拓宽思维 提升能力
——例谈圆锥曲线统一方程在切线问题中的应用
2018-04-24安徽省滁州中学
安徽省滁州中学
郭守静 (邮编:239000)
文[1]中介绍了圆锥曲线的离心率与统一方程,如图1,取过焦点F,且与准线l垂直的直线为x轴,点F(O)为坐标原点,建立直角坐标系,利用圆锥曲线的统一定义:
M∈{M||FM|=e|MH|}
其中e为圆锥曲线的离心率,定义p为圆锥曲线焦点到相应准线的距离.经过计算可以得到圆锥曲线(椭圆、双曲线、抛物线)在直角坐标系中的统一方程:
(1-e2)x2+y2-2pe2x-p2e2=0.

图1
课本中作为阅读与思考给出圆锥曲线的统一方程,课堂教学中笔者利用此结论,结合高考试题,论证圆锥曲线中具有统一性质的问题.本文通过几个具体实例谈谈圆锥曲线统一方程在切线问题中的应用.
引理已知圆锥曲线C:Ax2+Cy2+2Dx+2Ey+F=0(A2+C2≠0),则称点P(x0y0)和直线l:Ax0x+Cy0y+D(x0+x)+E(y0+y)+F=0是圆锥曲线C的一对极点和极线.
(1)若极点P在曲线C上,则极线l就是曲线C在点P处的切线;
(2)若过极点P可作曲线C的两条切线,MN为切点,则极线l就是直线MN.
文[2]中对上述引理作了充分的证明,本文就不作细证,由此引理可得对于圆锥曲线的统一方程而言,极线l:(1-e2)x0x+y0y-pe2(x0+x)-p2e2=0.
应用1圆锥曲线统一方程在切线问题中过定点问题

(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
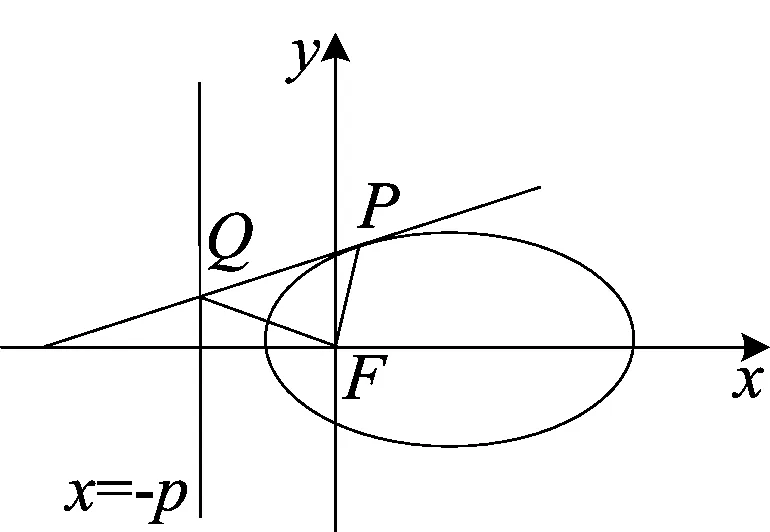
图2
文[3]对本题作了详细的证明,并由此题探究出圆锥曲线的统一完美的性质:如图2,已知点P是圆锥曲线C上一点,若曲线C在点P处的切线与曲线C的准线相交于点Q,则以PQ为直径的圆恒过该准线对应的焦点.
现用圆锥曲线统一方程可证明如下:
取过焦点F,且与准线l(与焦点F相对应的)垂直的直线为x轴,点F(O)为坐标原点,建立直角坐标系.
设P(x0,y0),椭圆的方程为:(1-e2)x2+y2-2pe2x-p2e2=0.
则切线PQ的方程为:(1-e2)x0x+y0y-pe2(x0+x)-p2e2=0
①

所以以PQ为直径的圆恒过该准线对应的焦点.
应用2圆锥曲线统一方程在切线问题中过定值问题

(1)求双曲线C的方程;
(2)过C上一点P(x0,y0)(y0≠0)的直线


现用圆锥曲线统一方程可证明如下:
圆锥曲线的统一方程:(1-e2)x2+y2-2pe2x-p2e2=0
②
P(x0,y0)为圆锥曲线上一点,则在P点处的切线方程为
(1-e2)x0x+y0y-pe2(x0+x)-p2e2=0
③


③中令x=-p,则-(1-e2)x0p+y0y-pe2(x0-p)-p2e2=0,



④


结合试题1、2,我们可以看到圆锥曲线统一方程在解决切线问题时有其特有的优势,课堂教学中以课本为主体,可以进行适当的拓展。对于圆锥曲线的统一方程:
(1-e2)x2+y2-2pe2x-p2e2=0.
当0
应用3圆锥曲线统一方程在切点弦问题中的应用

图3

本题是文[5]中对圆锥曲线切线的统一性质的探究,现用圆锥曲线统一方程来尝试解决.
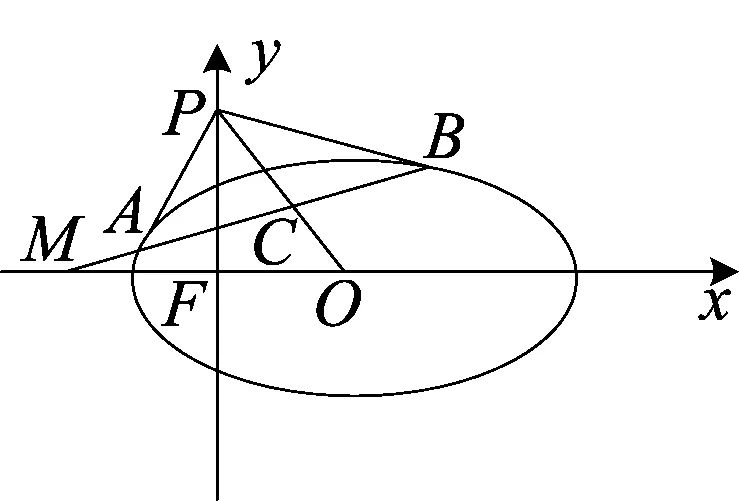
图4
解(1)如图4,取过焦点F,且与准线l垂直的直线为x轴,点F为坐标原点,建立直角坐标系设P(x0,y0),椭圆的方程为:(1-e2)x2+y2-2pe2x-p2e2=0.
则直线AB的方程为:(1-e2)x0x+y0y-pe2(x0+x)-p2e2=0
⑤
由题直线AB过点M(-p,0),代入直线方程可得:
-(1-e2)x0p-pe2(x0-p)-p2e2=0,
化简得到:x0=0,故PF⊥x轴.


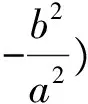
(3)将x0=0代入⑤中得:y0y-pe2x-p2e2=0,联立
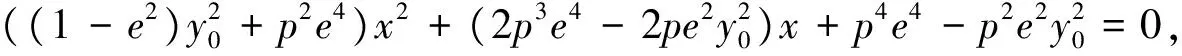
由C为AB的中点可知
代入直线AB方程可得

由P(0,y0),
即kPC=kPO,所以直线PC过原点.
受到篇幅限制,本文对双曲线和抛物线就不做详细论证,有兴趣的读者可以尝试一下.圆锥曲线具有许多的统一性质,而我们在研究相关问题时,可以借助圆锥曲线的统一方程来解决.在上述问题中,已知条件有焦点和焦点对应准线,此时用统一方程很方便.笔者也将会继续探究圆锥曲线统一方程的应用,并在课堂教学中积极探索,探求其规律性,拓展学生思维,激发学生学习解析几何的兴趣.也希望通过本文,能和广大读者一起探讨圆锥曲线的奥秘.
1 刘绍学.普通高中课程标准实验教科书数学选修2-1[M].北京:人民教育出版社,2007
2 邹生书.圆锥曲线极点与极线的一组性质[J].中学数学教学,2010(4):22-23
3 邹生书.对2012年高考福建卷理科解析几何题的研究[J].数学教学,2013(1):17-19
4 黄永生 杨丹.一道2014年江西高考题的推广[J].福建数学教学,2014(7,8):22-24
5 邱波.圆锥曲线切线的一个统一性质[J].数学通讯,2013(10):45
