把握降维分析思想 巧构立体图形截面

广东省广州市第六中学

璩 斌 (邮编：510300)

在高中立体几何里为了研究几何体的内部结构、性质及有关数量关系时，经常需要使用截面作为分析工具.因为特征性的截面可以在二维层面集中反映几何体的主要元素，揭示它们之间的内在本质联系，把几何体中的关键的内隐元素及其关系集中展现或暴露在平面图形上，将立体空间问题化归为二维平面问题，达到降维分析的目的.多面体的特征性截面的寻找与构造问题成了高中立体几何的常见问题，也是高中立几教与学的难点问题.高中立体几何教学的一个很重要的目的就是培养学生具有较强的空间想象能力，对截面寻找与构造问题的研究有利于立体几何教学目的的实现，近年来有关截面的问题在高考、自主招生考试和高中数学竞赛中经常涉及到.

所谓截面，是指一个平面与几何体相交所得的图形，包括边界及其内部，截面的边界叫交线.常见的截面有对角面、轴截面、直截面以及满足某些特殊条件的截面，截面问题常涉及：①建构截面并判断截面形状；②计算截面周长和面积；③研究截面图形的性质和最值等问题.要解决这些问题必须首先掌握多面体截面的建构，难点是找到“特征性”截面.对学生进行特征性截面作图训练正是培养和发展学生的空间想象力,综合运用立体几何知识的有效办法.

1 巧用平行性 建构立体图形截面

利用立体几何中的线面平行、面面平行的判断和性质定理来寻找立体图形截面.

图1

略；

(2)求面SCD与面SBA所成的二面角的正切角.

分析此题求二面角的关键是作出两个平面的交线，根据公理可知两平面若有一个公共点有且仅有过这个点的公共直线，现已知点S在交线上，寻找另一个公共点，延长BA、CD相交于点E，连接SE，则SE是所求二面角的棱，易证∠BSC是所求二面角的平面角.

例2(2005年全国高中数学联赛江苏赛区初赛)设四棱锥P-ABCD的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形. 则这样的平面α( )

A.不存在 B.只有一个

C.恰有两个 D.有无数多个

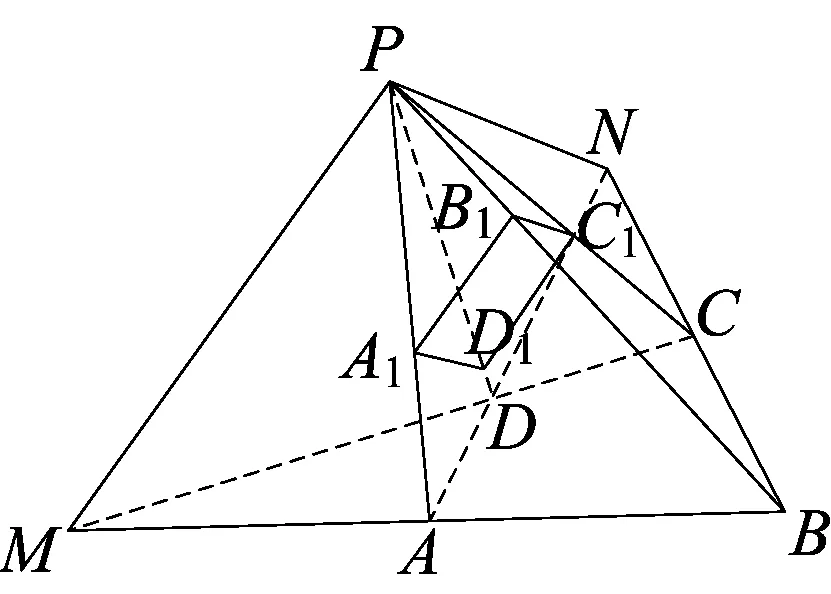
图2

分析：如图2,延长BA、CD,交于点M, 连接PM，则PM为侧面PAB与侧面PCD的交线；同理，PN为侧面PAD与侧面PBC的交线. 所要构造的平行四边形截面上的相应对边平行，则这组平行对边必同时平行于其所在对侧面的交线，即如图A1B1平行D1C1，则这组平行对边必同时平行于MP；反之，若截平面α平行此对侧面交线PM，则截面上的相应对边平行(降维分析思想的体现).

设由直线PM、PN所确定的平面为β，作与平面β平行的平面α与四棱锥的各个侧面相截，则截得的四边形是平行四边形(图中的四边形A1B1C1D1).可知，这样的平面α有无数个.故选D.

2 巧用“对称性”构造立体几何体的截面

充分利用长方体、正方体、正棱锥、正棱台和球等立体图形的对称性及其构成对称性的要素，寻找与构造多面体的特征性截面.例如长方体的对角线是长方体外接球的直径等的特征性来构造立体几何中的截面.

图3

例3如图3，已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球，求平面ACD1截球O的截面面积．

事实上，有关两个几何体相接或相切的问题，一般总要选取一个适当的截面，这个截面要能充分反映这两个几何体的特点，并能反映它们之间的关系，也就是所谓的特征性截面. 本例中，由于透视图上球O图形干扰了学生对平面ACD1截球O的截面图形形状的判断，教学中可以根据平行性和对称性，将问题转化为作平面A1C1B截球O的截面图形，则容易判断截面图形为正三角形A1C1B的内切圆．

例4半径为r的球内切于一个正三棱锥，求此正三棱锥的全面积的最小值.

分析半径为r的球内切于一个正三棱锥，由正三棱锥的对称性，内切球的球心必在棱锥的高上，因此应该根据这一特征过高SO1及一条侧棱作一截面，将空间问题转化成平面问题.

图4

如图4，过正三棱锥高SO1与一侧棱SC作截面，交棱AB于中点D，在此截面上，球的大圆O与SD及CD相切，OD平分∠SDC，设∠SDC=θ，则

例5如图5，在棱长为1的正方体内，有两球相外切且又分别与正方体内切.

图5

(1)求两球半径之和；

(2)两球的半径各为多少时，两球体积之和最小？

分析此题很多学生做起来很困难，主要是这个题对空间想象力要求比较高，若通过作特征性截面的办法来研究，可大大降低难度.

(1)由球以及正方体的对称性可知，可选取对角面D1DBB1为过球心的对角面见图6，从而找到了特征性截面.

(2)设两球体积之和为V，则

由于对称性，正三棱锥内切球和外接球的球心必在棱锥的高、长方体对角线必是长方体外接球的直径等特征性，是寻找立体图形特征性截面的重要线索.

3 巧用“相似性” 建构立体图形截面

利用平面图形的全等或相似的性质，计算数量关系，得出关键的数据，精准作图，构造立体几何体的特征性截面.

例6已知正三棱柱ABC-A1B1C1底面边长为10，高为12，过底面的一边AB作与底面ABC成600角的截面，求截面的面积.

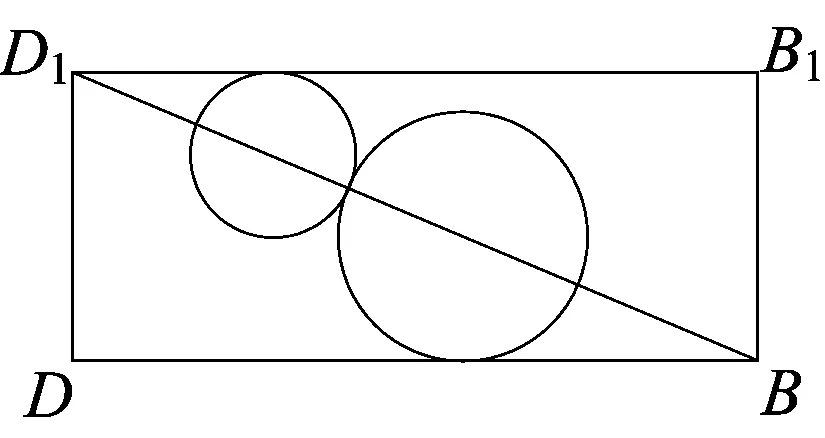
图6

错解设截面与棱CC1的交点为D，过C作CE⊥AB于E，连结DE，因为CC1⊥底面ABC，所以AB⊥DE，∠DEC为截面与底面ABC所成的角，因为

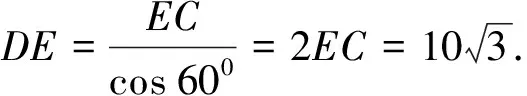
注意此解错在没有把截面的位置、形状等特征性情况搞清楚，可见截面的准确构建对其对解题的重要性.

而CC1=12，故D在CC1的延长线上，且CD=15.

连结BD交B1C1于M，AD交A1C1于N，连结MN，则ABMN为截面.

图9

例7如图9，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A、P、Q的平面截该正方体所得的截面记为S. (1)判断CQ的不同取值，所对应的S的形状.(2) 当CQ=1时，求S的面积.(2013安徽理科高考题改编)

分析本例已知截面S的一部分，即△APQ要构造出截面S，需要找到截面S与面ADD1A1的交线及截面S与面CDD1C1的交线.注意到这两交线必与棱DD1共点，即问题的关键在于确定这个点的位置.设截面S与棱DD1相交于T，则AT平行于PQ且AT=2PQ，从而DT=2CQ.

图10

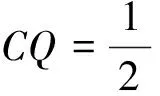
图11

图12

图13

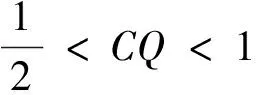
通过以上例题的分析，可见在立体几何中通过巧构立体图形的截面将复杂抽象的空间问题化归为平面问题，达到了降维的目的，从而有效的降低题目的难度，有利于正确解决问题，其关键是找到能代表其属性的特征性截面.画出正确的截面，因此在立体几何的课堂的教学中对学生进行截面作图方面的训练，使其掌握截面的建构和作图的常见方法，提升空间想象能力，思维能力，这对解决空间问题的能力是行之有效的方法.

1 傅钦志. 立体几何中的截面问题[J].中等数学, 2007(3)

2 侯典峰.正方体截面问题的再研究[J].数学通讯, 2011(7)

3 陈群星. 正方体截面研究[J].中学教研(数学), 2002(10):6-7

4 吴梁.作空间几何体截面的方法[J].中学教学参考, 2010(2):33-34

5 滕于忠.空间几何体截面的作法[J].河北理科教学研究, 2007(3):15-16