小学数学智慧学习探究

摘要：小学数学智慧学习，体现的是为未知而教、为未来而学的理念，重视引领学生灵活地调整学习策略，自觉地观照思维活动，生成并创造出自我学习智慧。教学的基本路径有重组教学资源、学会掘井思维、捕捉创新火花、移植师生经验、建设个人智库等。可用的策略有学会整理、学会转化、呈现直观、实现共生、学会阅读等。小学数学智慧学习，指向未来的适应力，提升带得走的学力，有助于发展学生的核心素养。

关键词：小学数学;智慧学习;实施路径;策略

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2018）02A-0088-06

一、瞻望智慧学习

进入新世纪，世界各国都在大力进行教育改革，其核心为发展学生的核心素养，致力于学生学习能力、学习品格的培养和提高。其主要路径为充分激发学生的主动性和积极性，使教学过程从以“教”为中心，转变为以“学”为中心，从知识授予，转向智慧生产，即“转知成智”。

新课改以来，尽管以学为先导的教学模式如雨后春笋般不断涌现，但深入实际我们不难发现学生的学习负担并没有减轻，只是由课内移到了课外，某种程度上反而加重了。此外课改实验中重知识技能轻思想经验，重共性结果轻个性体验，教与学不和谐统一等问题也较凸显。

直面以上问题，作为在教坛摸爬滚打了近三十年的一名小学教师，笔者所能做的就是改变我的课堂，影响我的学生，优化我的主张。在小学数学教学中，如何既遵循学科的特性，又关注学生的本性，让学生快乐、主动、充满智慧地去学习？我们认为，只有在教学中更多地关注学生智慧的发挥和发展，关注学生智慧学习方式的建立，关注学生主动、和谐、充满个性的发展，才能充分体现时代精神和课改需求。

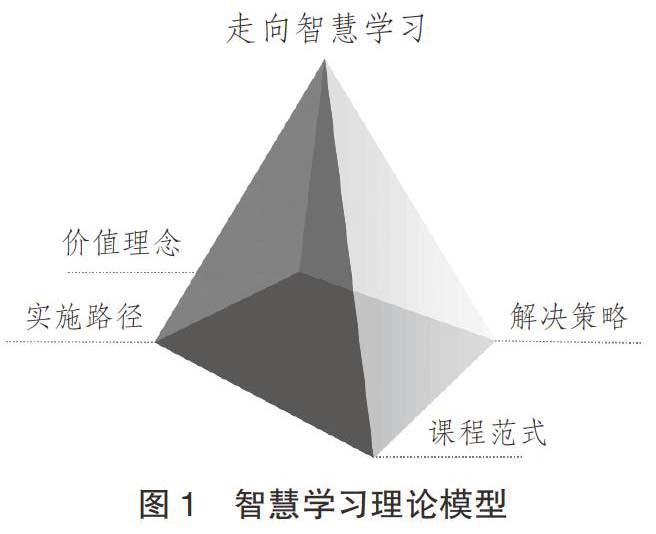
基于以上思考，我们提出了关注学生智慧学习的小学数学教学主张，并基本构建出了涵盖价值理念、实施路径、解决策略、课程范式等的理论模型，见图1。

二、解析智慧学习

智慧学习是智慧教育的重要组成部分，它有别于美国斯坦福大学王捷等学者所提出的基于信息化、全球化和协同创新与知识融合的全新学习方法。所谓小学数学智慧学习是指具有学生特质的智慧学习方式，是指学生通过师长的引领以及自身的努力，灵活地调整学习策略，自觉地观照思维活动，生成并创造出自我学习智慧的过程。这具体包括三层含义。一是明晰了“怎么教”。教师要侧重于学习方法、学习策略的教学。二是阐明了“怎样学”。学生要通过观照、反思，实现学习与创造的融合。三是指明了“走向哪里”。通过教与学的融合，最终学生形成属己的智慧学习能力。

观念是行动的指南，教学改革必须从教学观念的转变、更新开始。引领学生走向智慧学习，作为教师或家长需要确立几个观念——

（一）学习为人的全面的终身的成长而奠基

学习应该是人的成长过程，不仅是知识技能的成长，而且是身心各方面的成长;不仅是在学校、在教室里的成长，而且是整个人生的随时随地的成长。要从世界的变化看学习，从学习的变化看人生。

每个人都有适合自己的学习类型，都必须做自己学习的主人。人有语言、数学、空间、音乐、动觉、人际交往、自省等智能，有不同的学习类型。学习是人的本能，只要有心、用心，就能找到适合自己的智慧学习方式，同样也能够享受到由此带来的成功和快樂。

（二）学会怎样学习比学到具体知识更重要

终身学习要求我们把学习方法摆在重要的位置，经常处在学习的状态。要经常反思：我这样学下去行吗？有没有更好的学习方法？有了更好的学习方法，我们的学习就会事半功倍。

（三）我们的身体具有创造学习奇迹的潜能

多元智能理论启示我们，在我们的身体里，充满学习的潜在能力。每个人都有“神通”，每个学生都是亟待发展的天才。要相信我们自己，把身体里的力量发挥出来。一旦找到了适合自己的学习方式，我们将不断地创造学习的奇迹。

（四）婴幼儿的学习提供了最佳学习状态的样例

婴幼儿借助他们的活动、游戏和交流而学习。他们随时随地地学习，在学习中运用了所有能运用的感官和能力，包括无意注意、身体语言和潜意识。他们不怕犯错误，不耻下问，不厌其烦，不知疲倦，他们为自己取得的每一点成绩、每一点进步而欢喜。如果我们都能像婴幼儿那样学习，我们的学习效率就会有惊人的提高。

三、践行智慧学习路径

促进学生智慧学习的小学数学教学，力图通过一条经过实践检验的有效学习路径，让学生的学习行为开放起来。这种开放一方面表现在学习路径的多元选择上，另一方面表现在教学目的的投射远度上。

（一）建立数学知识间的联系

布朗思福特认为：卓越的学习者，其头脑中的知识组织是结构化的，散乱的知识不利于记忆、迁移、理解。要切实减轻学生的数学学习负担，就要帮助学生建立起数学知识间的联系，设法帮助学生提炼出合理的知识结构。

一种是将许多貌似不太相关的数学知识统整到一个思想框架内成为一个整体。如以“转化思想”为线索，让学生将相关的数学知识链接起来，有“数”方面的转化：小数、分数、百分数之间互化，各种运算之间的转化等;“形”方面的转化：有关图形面积或体积计算公式的推导、等积变形等;“量”方面的转化：名数的改写、数量关系之间的转换等……像这样鼓励学生用独具个性、智慧的方式重组教材，有利于学生进行整体学习、自主学习。另一种是引导学生不断提炼知识结构，这个提炼的过程是反复的，逐次递进的，需要经历一个建构（舍弃具体情境，看到本质的东西），到变构（打破已有结构，炼制新的意义），再到通达更优结构的过程。

拥有了这样一根“智慧链条”，我们的学生才能真正从零散、繁琐的知识中“立”起身来，对数学知识进行整体把握、灵活应用，从而进入一种智慧的状态。

（二）打通两种模式思维的联系

学习尤其是数学学习要有深度和创造力，需要在专注模式与发散模式之间自然转换。专注模式下的数学思维活动是利用理性、连贯、分解的途径直接解决问题。专注模式与大脑前额叶皮层集中注意力的能力相关。[1]而发散模式似乎与任何一个特定脑区的关系都不太密切，它更像是弥散于整个大脑之中。当学生在一个问题上挣扎许久而不得思路，发散思维会冷不防地提供一个新点悟。当学生放松注意力，任由思维漫步、驰骋时，发散模式思维就出现了。

在数学教学中培养学生的掘井思维，能促使学生在专注思维与发散思维间互动往来。如在教学“已知男生的和女生的相等，求男生人数和女生人数的比”这一内容时，教师先让学生把注意力集中在问题上，每个学生充分调动已有的知识、经验，启动各自的专注模式思维，尝试用自己最擅长的方法独立解决问题。在相互交流算法的过程中，学生的注意力暂时得到放松，各自不同的算法在脑中来回穿梭。不经意间，发散模式思维来临了，基于他人又超越他人的不同方法不断涌现。一道看似平常实则开放的数学问题，在学生两种模式思维的持续作用下，衍变成一个丰实立体、创意无限的知识系统，这样的学习无疑是充满着智慧、极富生命力的。

学会掘井思维，教师要为学生选准一个切入口。它可以是一个关系句，可以是一组信息，也可以是一个开放性的问题。在教师的引导下，学生从各个角度去分析、去思考，去寻觅新联系，去获取新突破。学会掘井思维，教师要为学生提供一个着力点。对于所提供的素材，教师自己首先要有一个全面、深入的思考，然后选择一个最贴近学生实际的角度展开研究，从而产生新联想，获得新进展。学会掘井思维，教师还要为学生创造一个思维场。既要培养认真倾听的良好习惯，又要营造热烈交流的民主氛围。在倾听、交流中，学生的视界得到拓展，思维产生共振，智慧获得生长。

（三）发现突破与创新的联系

学生创新意识的培养，需要一定的契机。学习过程中出现的一些疑难、困惑，会让学生不满足，同时也能促使学生尽力扭转这种不平衡的状况。为消除这种不平衡，就需要打破常规、突破限制，一些奇思妙想就会应运而生。学生的奇思妙想中孕育着创新的火花，如果能及时地捕捉并加以合理利用，就会产生创新的成果。

创新的希望火花，还产生于平常悉心的观察。如在除法计算中怎样准确、快速地试商一直是一个教学难点，很难找到一个有效的解决办法。一次在计算“8151÷13”时，一名学生说把13看作20来试商，引起哄堂大笑。为激发学生的求异思维，教师补充道：“说不定这是个创造性的试商法呢？”这名学生灵机一动，脱口而出：“先把13看作20来试商，再把13看作10来试商！”教室里一下安静下来，不一会儿几只小手同时举了起来，并迫不及待地喊起来：“商是6！”[2]（把13看作20来试商，百位商4;看作10来试商，商是8。4与8的平均数是6，百位应该商6）“平均试商法”由学生直觉地创造出来。

学生心智的觉醒虽极其重要，但又是转瞬即逝的。这就需要教师用自己的教育智慧有意识地去开发它，敏锐地去发现它，尽力地去留住它，想法设法去丰富它。一方面我们需要创设和营造一种生动的情景和宽松的氛围，激发学习兴趣，激活学生思维，让学生敢想、敢问;另一方面我们需要多长个“心眼”，及时捕捉学生思维中的一些哪怕是一丁点儿的亮点、生长点，用力去保护，用心去点拨。同时教师也要引导学生用心去捕捉周围生活和日常学习中的一些“亮光”，用它来照亮创新的思路，开启智慧的大门。

（四）沟通直接、间接经验间的联系

杜威认为教育的定义应该是经验的解放和扩充。小学数学教学要特别注重与学生丰富多彩的经验的对接。这样的经验不一定是直接的，也可以是間接的，还可能是类似经验的迁移。“只有当相继出现的经验彼此结合在一起的时候，才能存在充分完整的人格。”[3]因此，我们应改变过多依赖教师经验展开教学的状况，不断勾连知识与经验、学生经验与教师经验、直接经验与间接经验的联结，从经验认知出发，通过对照、联系、体验、探究，提升学生数学学习的品质与境界。

杜威还指出：无论如何，一个人应能利用别人的经验，以弥补个人直接经验的狭隘性，这是教育的一个必要组成部分。[4]在挖掘、利用学生经验资源的同时，教师也应适当地向学生提供、呈现自己的经验资源，从而使师生双方实现经验互补，智慧共享。师生联合不仅能让学生发现自身经验的意义，还能有意识地考虑别人的经验，并将它迁移到新的经验上加以运用，这是智慧的命脉。

移植师生经验，首先，要唤醒学生经验。只有在民主平等的氛围中，学生才能畅所欲言，向教师和同伴展示自己的生活、学习经验。其次，要实现经验共享。教师要有利用师、生经验资源的习惯和意识，要尽力把新的知识与自己已经知道的知识联系起来，用自己已有的经验去生发出新知识，这样的学习才有效。反对灌输，主张个性;反对外部制约，主张自由活动;反对单向学习，主张多向学习，从经验中学习;反对固定的目的和教材，主张熟悉变化着的世界……这些蕴含教育哲学的教育实践，值得学习和借鉴。

（五）发掘自我与世界的联系

生理学研究发现，运用书写整理思绪或创意，有刺激头脑、激发脑的生机的作用。人体肌肉中有种感觉器“纺锤肌”，附着在它周围的肌肉由于动作呈紧张状态时，其本身也会受到刺激，并立即将刺激通过神经传导到延髓网状结构处，使意识作用趋于活跃。因此勤于动笔的人，头脑往往更为灵活，思路更为畅快。“智慧在指尖跳跃”，说的就是这个道理。

勤读助思。读书本，读新鲜事，一旦读出了味道，读出了创意，就毫不犹豫地记录在卡片上，为属于自己的智慧库增添储备，是发展创新智慧的一项“基本建设”。当学生在数学学习上遇到问题时，比较智慧的做法是先不直接告诉学生解决问题的方法，而是引领学生先独立思考，再通过交流、讨论，或课后自己去查找、阅读有关的资料，最终获得解决问题的最佳方法。如学生尝试解答蔡金法教授设计的一道题：“餐厅里有一些大小一样的比萨饼。7个女孩平分2个披萨饼，3个男孩平分1个披萨饼。每个女孩与每个男孩相比，谁分的饼多？”在学生用常规的策略（先求出平均每个女孩、每个男孩分的饼数，再用通分、化小数的方法来比较）解答后，有学生追问：“美国学生是怎样解答的？是采用的常规策略，还是非常规的方法？”教师并没有直接呈现美国学生的解法，而是引导学生先独立思考，再在小组内进行交流，课后再上网进行搜索。这样每个学生至少掌握了八种不同的解题方法，并且从中筛选出了最具创意、最优化的解题策略和方法。

勤“读”与勤“笔”相结合，不仅能催生创意思维，丰富文化积淀，还能提高主动学习的能力和水平。如学生尝试用多种方法解决了“分饼问题”后，以《谁分的饼多》为题，完成了一篇数学日记或数学小论文。学生获得了“要冲出常规方法的束缚，我们也能像美国学生那样创造各种不同的方法”“我们不应满足于找到最优方法，而应先发散自己的思维，然后再从中找出最好的方法，这样我们的想象力和创造力才会越来越强”等诸多独到的体验和感悟。

智慧学习路径的选择，其实是寻求影响学习的各要素之间联系的一种哲思与探行。诺尔·诺丁斯说：一切教育效果的评判标准，取决于学生究竟学了什么、学得如何以及继续学习的潜力与愿望。在教师的引领、同伴的启发以及自我的观照下，每一名学生都能形成比较稳定的、智慧的学习方式。一旦学生形成了一种智慧的学习方式，将引起学习行为、学习能力的比较持久的改变，虽然这些变化不一定表现出外显的行为，但却让学生终身受益。它既能带给学生知识和能力，更将带给学生智慧、希冀和力量。

四、践行智慧学习策略

策略是从观念走向行动、从理论走向实践的方式和方法。有了正确的教育观念，还得进一步把观念转化为可操作的策略，这样，关注学生智慧学习的小学数学教学才能真正落地。

（一）学会整理——学生智慧学习的“脚手架”

操作要领：

1.尝试归纳。学生在自学教材时，试着对教材内容进行批注，概括出主要内容;一堂课结束后，让学生在书本留白处记下本堂课的主要内容;一个单元学习结束后，让学生试着画出知识结构图。

2.个性设计。当学生能够从数学学习中获得个人意义时，学习的效果特别显著。引导学生对一堂课、一个单元的学习内容进行个性化整理，其实是对学习成果系统化、合理化、艺术化的再挖掘、再发展。各具特色的知识网、知识树，赋予了个人独特的意义，蕴含着一定的创造因子，将成功纳入学生的“智慧宝库”。

3.展示交流。定期对学生整理的知识结构图进行展评，有利于学生的自我调整与完善，更有利于学生将整理策略内化于心，外化于行。

（二）学会转化——学生智慧学习的“密码箱”

操作要领：

1.聚焦问题。学生收集一些可生发、可拓展的数学开放题，并尝试用多种不同的方法来解答。

2.积累方法。教师结合具体问题，帮助学生提炼常用的转化方法，如数形转化、关系转化、视角转化等。有了这些具体方法的支撑，学生对转化策略的应用才会驾轻就熟、了然于心。

3.走向综合。教师可通过综合实践，提高学生综合应用数学知识、数学方法解决实际问题的能力，引领学生走向生活，使他们意识到并不是所有的生活问题都可转化成数学问题，而数学知识的丰富性、立体化决定着转化策略应用水平的高低。

（三）呈现直观——学生智慧学习的“简化器”

操作要领：

1.建立认知图式。数学概念、数学定理的几何意义的阐释，有利于学生形成表象，促进学生的知识记忆，同时，学生在这个过程中积累了表象建构经验。这种经验的丰富又增加了各种直观化发生的可能性，同时为问题解决过程中的表象迁移提供了潜在的可能。

2.利用直观推理。在独立解决问题时，教师应允许学生用一些比较直观的方法（如图示法、假设法、特殊值代入法等）来分析问题。直观推理经验的积累，有利于提高学生自我构建图式的能力;直观推理经验的优化，有利于实现从直观到抽象的跨越。

3.实现数形对应。引导学生进行数与形的转换、数与形的对应，有益于学生拓宽学习视野，打破思维界限，从而实现整体学习、创新学习。

（四）实现共生——学生智慧学习的“加油站”

操作要领：

1.唤醒个体经验。通过情境创设，成功唤起学生的先有经验，是实现经验扩充的先决条件。

2.分享师生经验。通过合作学习、交流分享，有利于学生修正自己的错误经验，强化、优化自己的正确经验，从而不断丰富、完善各自的经验系统。

3.筛选网媒经验。利用搜索引擎、微信平台，比较不同的方法与经验，学生自身经验得到扩充与发展，从而赋予新的意义和价值。

（五）学会阅读——学生智慧学习的“营养餐”

操作要领：

1.激发兴趣。小学数学故事课程的建设，使学生在读故事、品故事、讲故事、编故事中体验到数学阅读的满足感。

2.自我设问。结合数学阅读材料，教师引导学生自行发现问题、提出问题，并尝试自己分析问题、解决问题。通过自问自答、互问互答，能有效提高学生的数学阅读水平。

3.实现链接。借鉴脑科学的最新研究成果，大脑具有一种迁移功能（它可以将在一种情境下所学习的内容，以一种可能经过调整的或概括化的方式应用于另一种情况）。提高链接式阅读，能使学生对数学知识的理解更加全面、深入，便于学生看清數学知识的体系构成与发展脉络，从而不断提高学生整体学习的能力和水平。

相对而言，整理策略对应重组教学资源这一智慧学习路径，转化策略对应学会掘井思维的智慧学习路径，直观策略对应捕捉创新火花的智慧学习路径，共生策略对应移植师生经验的智慧学习路径，阅读策略对应建立个人智库的智慧学习路径，但这只是为了理解与表达的方便，实际上，它们的关系不是简单的对应关系，而是复杂的多向关系。任何一项好的策略都同时体现了若干条理念，而任何一条好的理念、路径也同时需要多项策略去落实。

关注学生智慧学习的小学数学教学除了要有理念的指引、路径的选择及策略的支撑，还需要建立一套科学的评价方式。小学数学智慧学习评价的目的就是要让智慧教学回到本意，即教学生学会学习。小学数学智慧学习评价应包含三层含义：一是评价教师是否侧重于数学思想、数学学习策略和方法的教学。如果教师只满足于数学知识的讲授、技能的训练，不善于提炼蕴含于数学知识之中的数学思想方法，不善于捕捉、开发蕴含着重要数学方法的现实情境、核心问题，不善于改进传统的教学方式，那么这样的教学是不大可能促进学生智慧的发展的。二是评价学生是否形成了属于他们自己的数学学习方式。离开了教师的教，学生能不能主动地、自主地学习;面对相对比较陌生、有难度的问题，学生解决问题的思路是否单一，能否调动已有的经验逐步走出困境，在相互交流、倾听的基础上有没有形成自己独到的见解等。学生的这些外在表现折射出的是他们内在的学习方式、思维方式的建立。三是评价教师的教学是否真正以学生学会学习为核心。真正的智慧教学，教师心中是有“纲”的，以发展学生核心素养、促进学生智慧发展为纲;教师心中又是有“目”的，以核心问题为抓手，以策略、经验的积累为根本。这样的“纲举目张”，方能体现以学生学会学习、智慧学习为核心。

關于“智慧”，古今中外的大家、学者有着各自不同的理解。尽管引领学生走向智慧学习目前只是一种理想、一种愿景，但有了一群挚爱后生的智者的指引，更有了一群志同道合的同伴的携行，我们终将朝着这一理想愿景不断地靠近！

参考文献：

[1][美]芭芭拉·奥克利.学习之道[M].教育无边界字幕组，译.北京：机械工业出版社，2016：10.

[2]任卫兵.小学数学智慧学习的实施路径[J].江西教育，2017（6）.

[3][4]邱磊.杜威教育箴言[M].上海：华东师范大学出版社，2015：7.18.

A Study of Primary School Mathematics Intelligent Learning

REN Wei-bing

（Tongzhou Center for Teacher Development， Nantong 226300， China）

Abstract：  Primary school mathematics intelligent learning embodies the idea of teaching for the unknown and learning for the future， emphasizes students flexible adjustment of learning strategy， consciously focuses on thinking activities， and generates and creates self-directed learning wisdom. The basic paths to teaching are restructuring teaching resources， learning to thinking， capturing creative sparks， transplanting teacher-student experience and building personal think tanks. Corresponding strategies include learning to sort out， learning to transfer， presenting intuitively， realizing symbiosis， and learning to read. It points to the future adaptation ability and promotes transferable learning ability， which is helpful to develop students core accomplishments.

Key words： primary school mathematics; intelligent learning; implementing path; strategy