基于转速信号的旋转机械故障诊断方法研究
2018-04-08李仲兴柳亚子王子豪薛红涛
李仲兴,柳亚子,王子豪,薛红涛
(江苏大学 a.汽车与交通工程学院; b.机械工程学院, 江苏 镇江 212013)
轮毂电机式电动汽车由于结构紧凑、污染小、电机响应快等优点[1],已经成为汽车领域新的研究方向。轮毂电机式电动汽车配置4个轮毂电机,每个轮毂电机的正常运行可以保证车辆行驶的稳定性和安全性,然而一旦某个电机运行出现故障将导致汽车的失稳。为保证轮毂电机安全、稳定、高效地运转,有效避免车辆严重故障或事故的发生,有必要开展对轮毂电机的状态监测和故障诊断理论方法研究。
阶次跟踪法是一种角域频谱分析方法,可有效消除旋转部件转速变化对信号分析产生的影响,在旋转机械故障诊断、噪声分析等领域应用较为广泛。目前国内外许多学者针对旋转机械的阶次跟踪诊断技术进行了大量研究,也取得了一定的成果。在阶次算法方面,宋宝玉等[2]、陈向民等[3]将阶次跟踪与角度域同步平均、形态分量分析等算法结合在一起,提高了阶次分析的可靠性;Borghesan等[4]提出速度同步阶次分析,利用瞬时速度的优势提高阶次计算结果的准确度;Sapena-Bano等[5]使用谐波阶次分量作为独立的故障变量来跟踪分析感应电机故障,减少了阶次分析算法的计算量。在工程应用方面,朱茂桃、王科盛等[6-8]利用阶次跟踪法对齿轮箱中齿轮以及滚动轴承故障进行准确定位与分析;Alwodai、Akar等[9-10]国外学者运用阶次跟踪对感应电机静态偏心故障及定子故障进行有效诊断。
阶次跟踪方法以旋转轴旋转频率为基准,将转速信号作为中间量,实现对振动信号的角域重采样,从而使得旋转机械振动信号由时域非平稳性转化为角域平稳性。但是在一些工程应用中,无法同步获取转速和振动信号,且传统阶次跟踪方法可能会因忽略了中间量——转速信号而产生非正常波动,这在一定程度上限制了故障特征的提取与分析,影响了阶次跟踪方法的适用范围,降低了旋转机械故障识别精度。因此,本文提出一种新的方法——阶次自分离法,并将此方法运用在轮毂电机的故障诊断上。
1 阶次自分离方法
在传统阶次跟踪分析中,阶次(Order,O)的定义为振动信号频率与基准频率或参照旋转轴旋转频率的比值,其表达式如式(1)所示[11]。
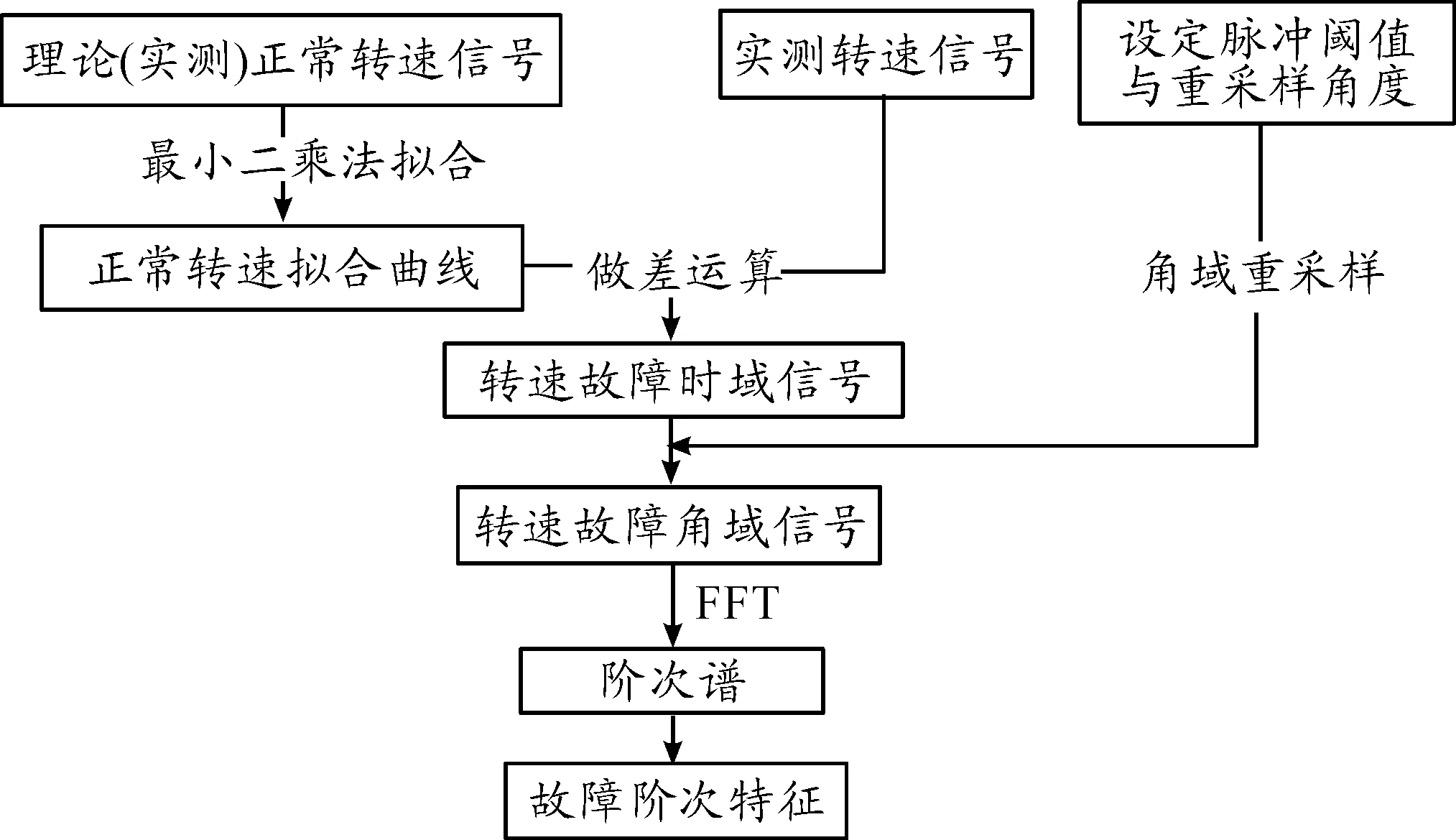
图1 阶次自分离方法流程
(1)
式中:fsignal为振动信号频率;fbase为基准频率或参照旋转轴旋转频率。
阶次自分离方法摆脱了传统阶次跟踪分析方法需同时采集转速信号和振动信号的局限性,以转速信号为研究重点,提取旋转部件转速信号中由故障引起的非正常波动成分,并利用转速信号跟踪该非正常波动成分将其转换为角域信号,进一步通过重采样、傅里叶变换等手段,找到转速信号中因故障而引起的转速波动信息与旋转机械故障状态之间的关系。因此,相比传统阶次跟踪方法,阶次自分离方法中阶次被定义为转速故障信号频率与参考轴旋转频率的比值,即式(1)中fsignal为转速故障信号频率。为便于叙述,将正常状态下转速定义为正常转速信号,在故障状态下由故障引起的转速波动成分定义为转速故障信号。阶次自分离方法的实现流程如图1所示。
传统阶次跟踪方法根据时间与转角所呈关系设定等角度间隔的重采样时刻,再采用线性拟合、多项式拟合或样条插值拟合,便可将时域中的故障信号映射到角域中来,完成角域重采样。阶次自分离算法则需先将转速信号转化为转角信号,这一问题可通过梯形积分法加以解决。
设ti时刻对应的旋转部件转过的转角为θi,转速为ωi(ωi=π·ni/30),则:
(2)
式中M为插入重采样时刻后的总采样点数。
2 基于仿真信号的阶次自分离分析
轮毂电机在正常运行状态下,转速输出信号nnormal由理论转速信号和噪声信号组成。当电机发生异常时,其实测转速信号nspeed由理论转速信号和转速故障信号、噪声信号3部分组成。为了验证阶次自分离方法对故障信号特征提取的有效性,假定轮毂电机在正常和异常状态下产生的噪声信号是相同的,于是在故障状态下仿真信号的模型可设为:
nspeed=nnormal+nwave
(3)
式中:nnormal为正常转速信号;nwave为转速故障信号。
本研究假设正常转速随时间的变化呈二次曲线规律,即
nnormal=a2t2+a1t+a0
(4)
式中a0、a1、a2为待定系数。
由于电机故障往往包含多种频率成分,因此假设转速故障信号nwave由2种频率与振幅不同的故障信号组成,且波动频率与旋转部件旋转频率呈一定阶次关系。当故障成分为矩形波信号时,其随时间的变化关系为
(5)
式中:O1、O2为矩形故障信号的阶次;A1、A2为矩形故障信号的振幅。
利用等时间间隔转速信号nspeed进行故障信号分离诊断。当a0=300,a1=-120,a2=60,O1=10,O2=5,A1=10,A2=5时,转速-时间曲线如图2所示。
通过对正常转速信号进行二次曲线拟合,同时将nspeed与拟合结果做差,得到时域内转速故障信号,如图3所示。对分离出来的转速故障信号进行角域重采样,重采样后的角域信号如图4所示,对角域内转速故障信号进行傅里叶变换得到阶次谱图。图5为该故障信号的阶次自分离诊断结果。从图5中可得到该转速信号中存在两个故障信号,其中:一个信号阶次为4.99,引起转速波动幅值约为10.02 r/min;另一个信号阶次为10.01,引起转速波动幅值约为23.38 r/min。
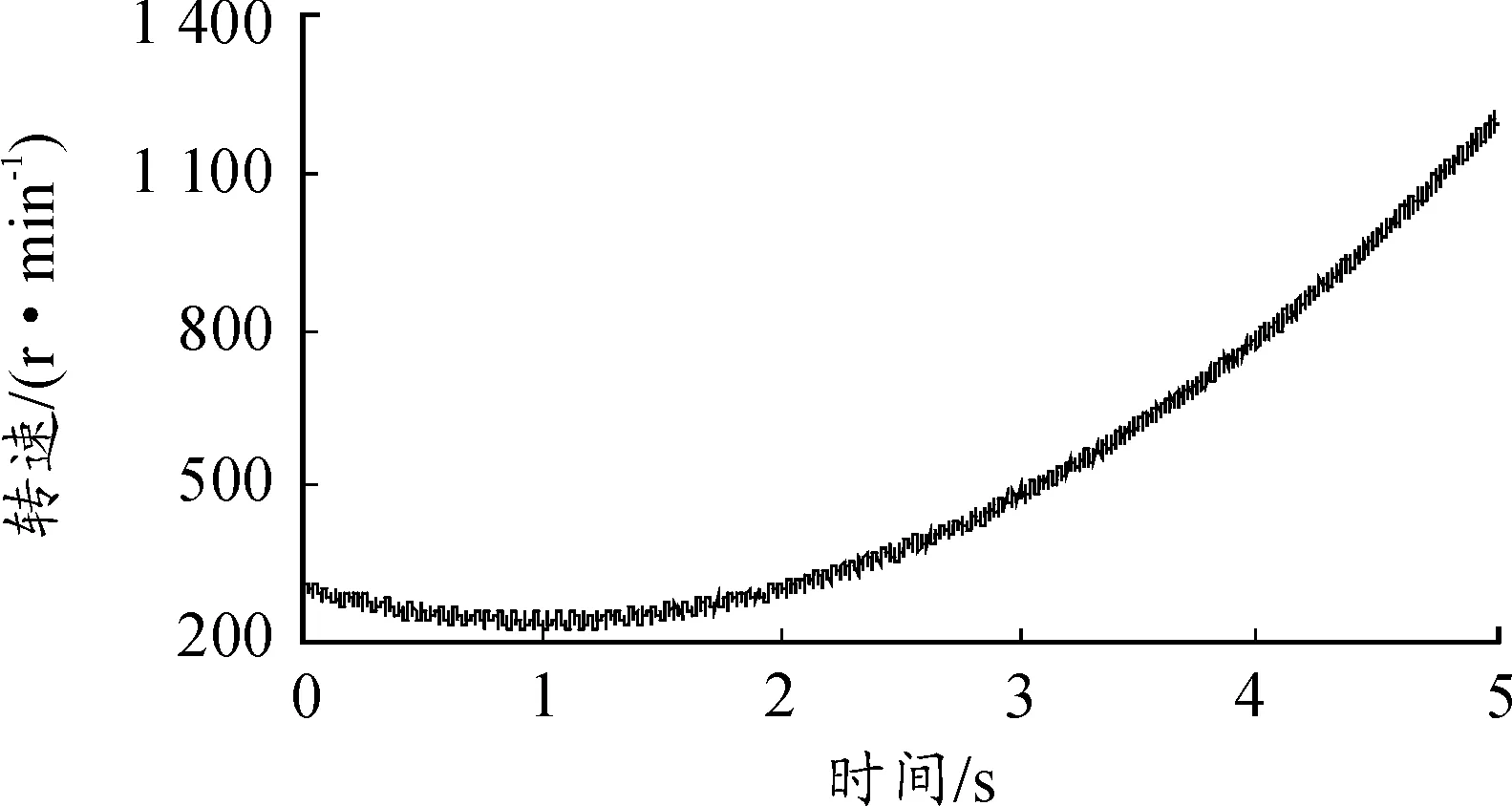
图2 多矩形故障下转速信号
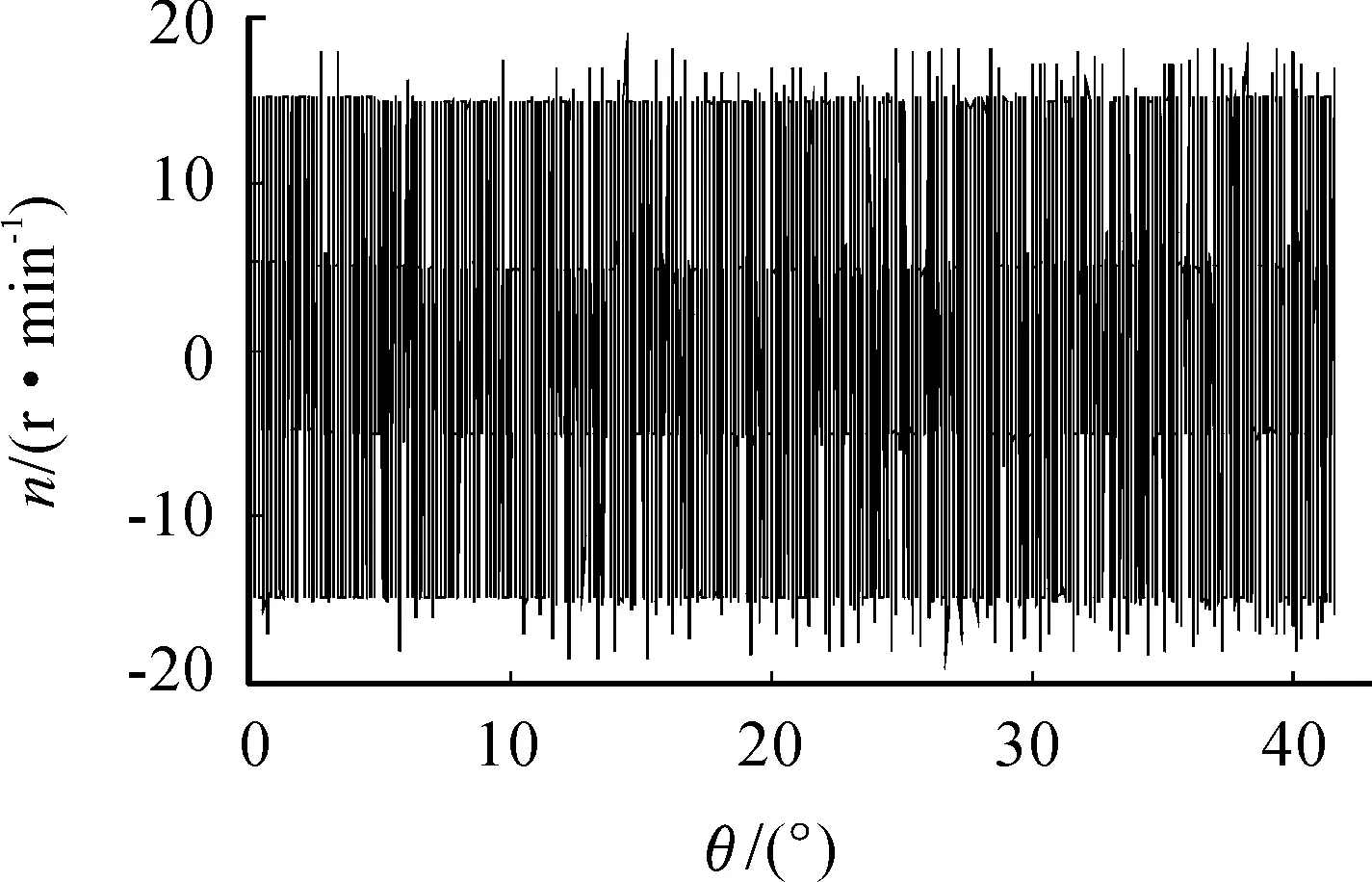
图4 转速故障信号(角域)
由此可见,阶次自分离方法既可以精确识别故障信号的阶次,还可以准确判断转速故障信号的波动幅值。
3 实验验证
3.1 实验系统
为进一步验证阶次自分离方法在轮毂电机故障诊断中的可行性,本文设计了轮毂电机漏电实验,并利用所提出的阶次自分离方法对其漏电故障进行诊断。
实验时,采用轮毂电机故障诊断实验系统,设置采样频率为20.48 kHz。当电机绕组发生相间漏电故障,即电枢回路电阻发生变化时,电机绕组部分的输出功率降低,电机电枢端电压将发生变化,从而导致电枢电流改变,进一步影响电机输出转速。所提阶次自分离方法适用于波动频率随转速大小变化的故障信号,因此综合考虑电机三相电流的交流特性,在漏电故障支路设有整流二极管,使得故障支路上产生频率随转速增大而增大的交变方向脉动电流,同时利用功率电阻阻值消耗电机功率。
为方便对不同漏电程度故障进行阶次自分离诊断,由多个二极管与不同阻值的功率电阻、开关a-f等构成漏电故障。漏电支路设置在电机A、B两相之间。
3.2 实验结果
利用Arduino微控制器电路板控制电机转速由0匀加速增加至最高转速。选定功率电阻阻值为6 Ω,切换漏电故障支路模块上硅二极管导通个数分别为0、5、10个,即漏电故障支路截止导通电压为0、2.5、5 V,将这3种状态分别记为1号漏电状态、2号漏电状态、3号漏电状态。图6所示为正常状态和1号漏电状态下的电机三相电流,从图6中可以看到:相比正常状态,发生漏电故障时A、B两相的相电流在某一固定状态内间歇性地发生规律性波动,C相电流无显著波动。由该电流信号变化特征可知,当轮毂电机发生相间漏电时,其输出转速中存在由漏电故障引起的非正常波动。
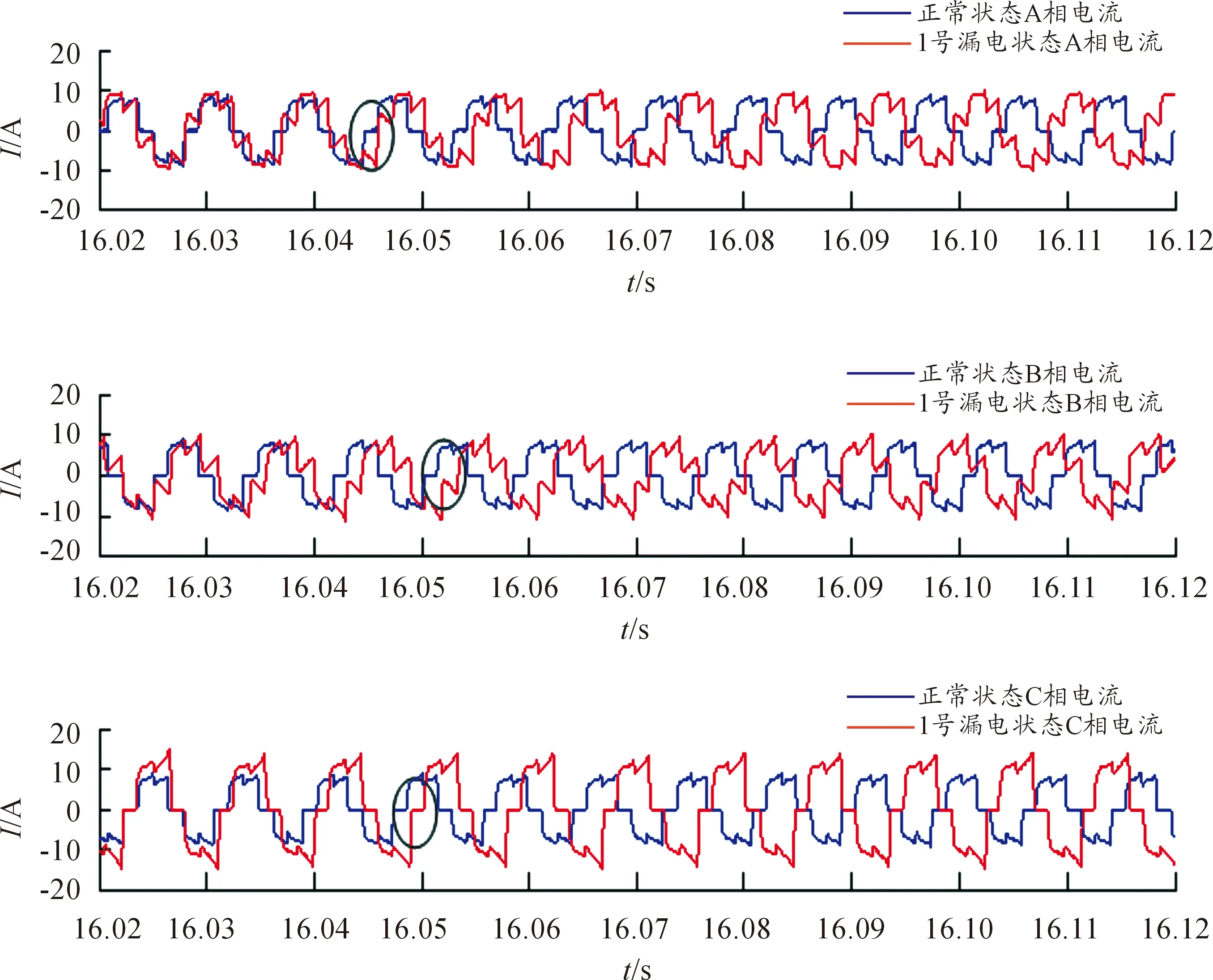
图6 正常状态和1号漏电状态下电机三相电流
利用所提阶次自分离分析方法对电机转速中存在的非正常波动进行故障诊断。图7为正常状态和3种漏电状态下的电机输出转速。本文以1号漏电状态为例,详细分析其阶次自分离处理过程。
基于拟合后的正常转速信号对1号故障状态下的转速信号进行阶次分离分析,提取转速故障信号,如图8所示。从图8中可看到:转速故障信号为一幅值随时间逐渐降低的信号,带有明显的趋势项。其原因在于:对电机来说,漏电故障引起的波动成分在作用一段时间后将使得电机整体输出功率减小,会导致其输出转速整体下降,即表现为带有趋势项的波动信号。由于该趋势项并非幅值恒定的直流分量,而是类似于二次曲线的变化规律,故基于最小二乘法消除故障波动成分中的趋势项[12-13],得到消除趋势项后的时域转速故障信号,如图9所示。
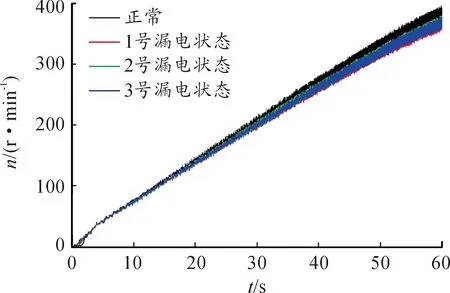
图7 正常和漏电状态下电机转速信号
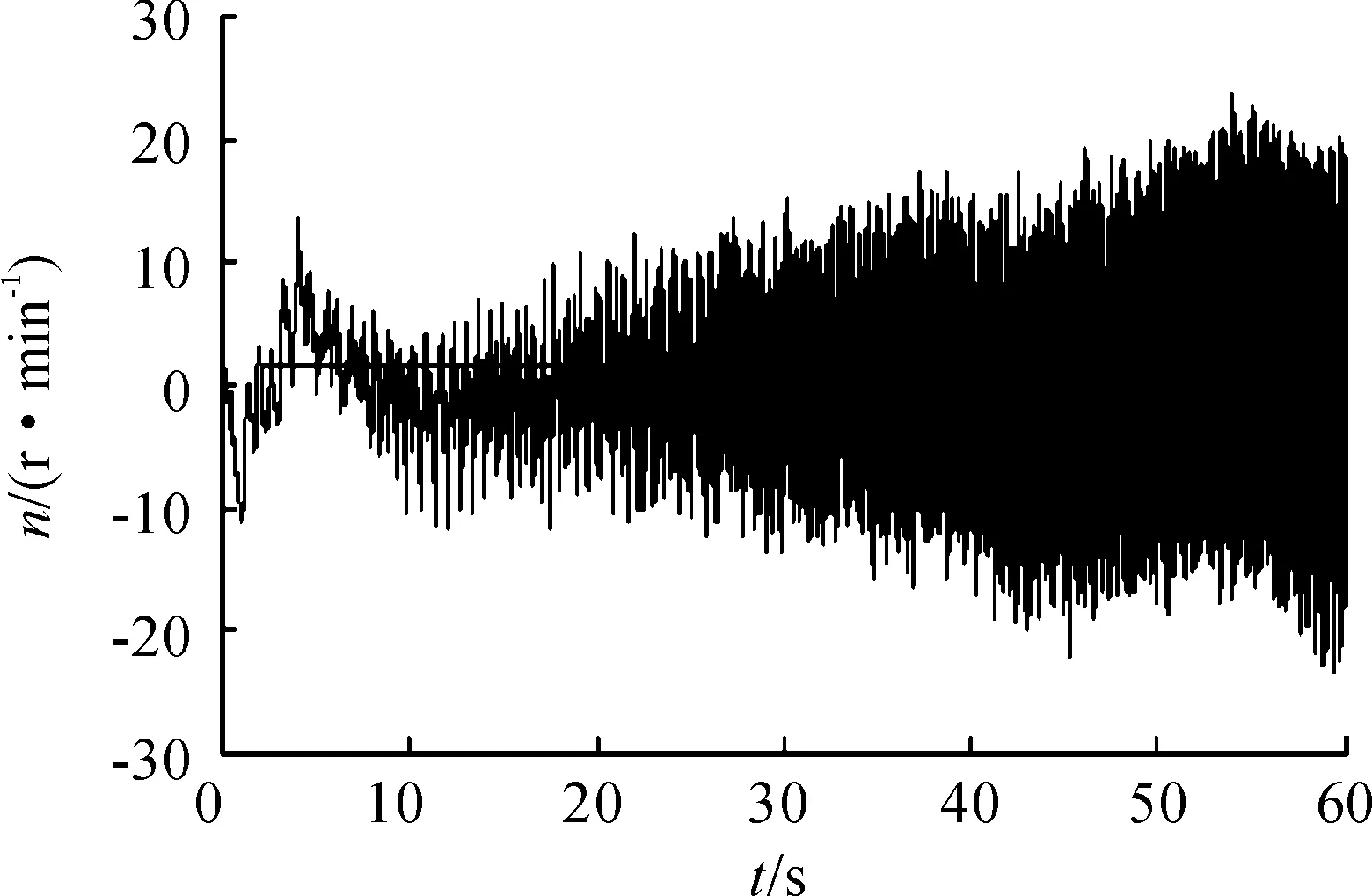
图9 转速故障信号(时域)
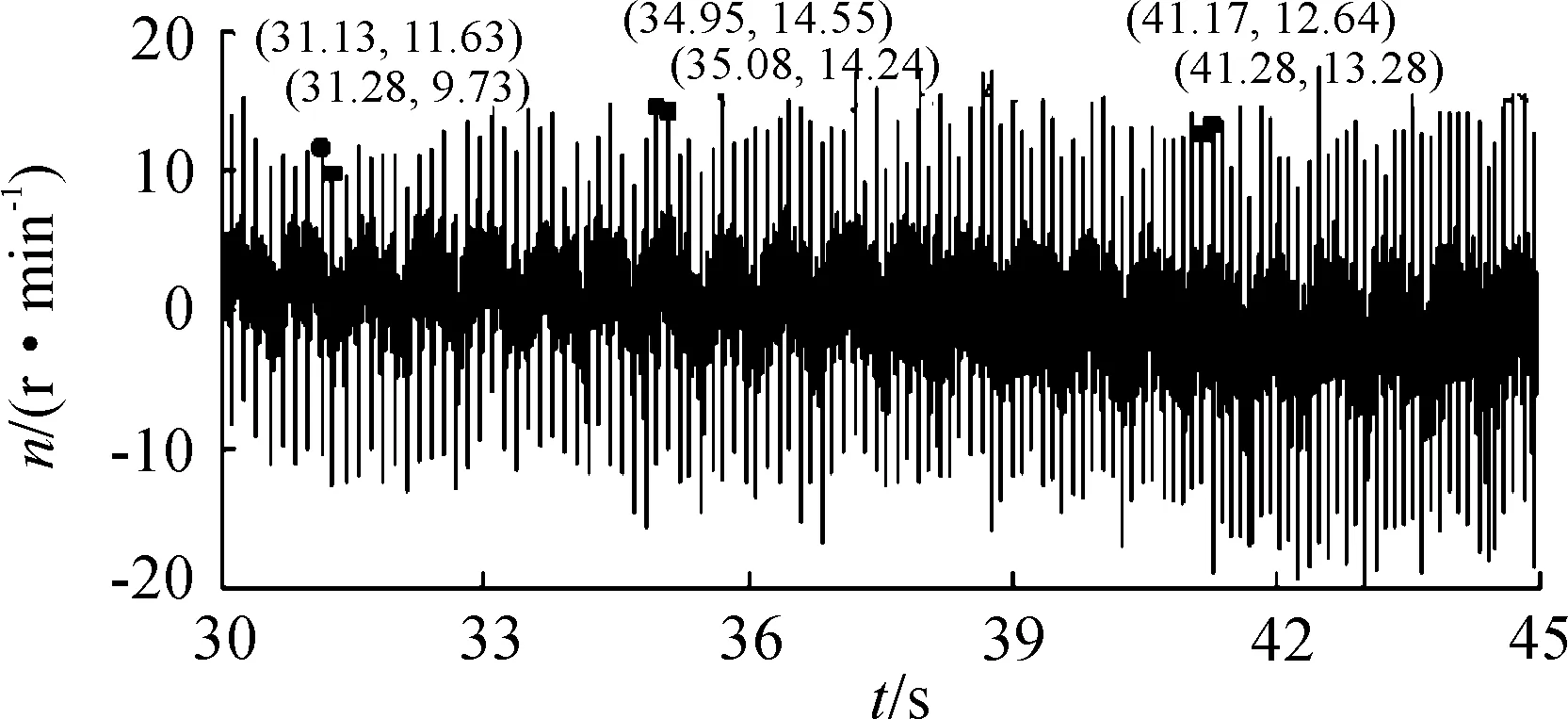
图10 局部转速故障信号(时域)C
从图9中可以看到:消除趋势项后的转速波动成分为幅值围绕零附近上下波动的非平稳信号,随着时间的增加,电机转速持续不断增加,波动幅值越来越大。图10为图9的局部图,图中标注的峰值时标间隔分别为0.15、0.13、0.11 s,可以看出波动的频率也随转速增大而提高。对转速故障信号进行角域重采样,重采样频率为30.72 kHz,采样角度θi为2π/30 720=0.017 3°,重采样点数为222=4 194 304。图11和图12分别为角域内转速故障信号和其局部图,可以看出:经过重采样后的转速故障信号频率变得平稳,峰值时标角度间隔均为0.7r。
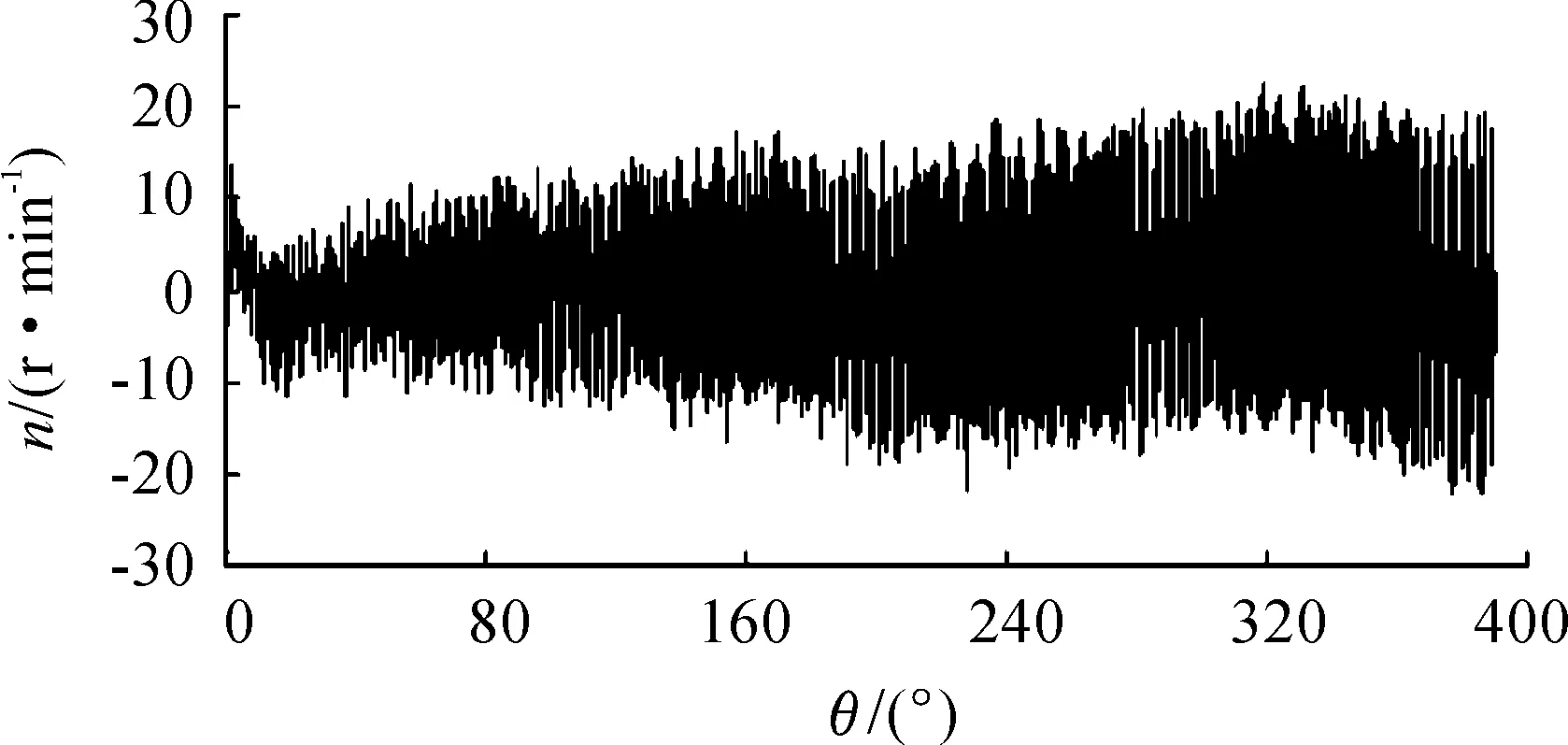
图11 转速故障信号(角域)
将重采样后的转速故障信号进行快速傅里叶变换,得到其阶次谱图。同时,对正常转速信号和其余两种程度的漏电故障进行阶次自分离分析,图13为正常转速信号与3种漏电状态下转速故障信号的自分离诊断结果。
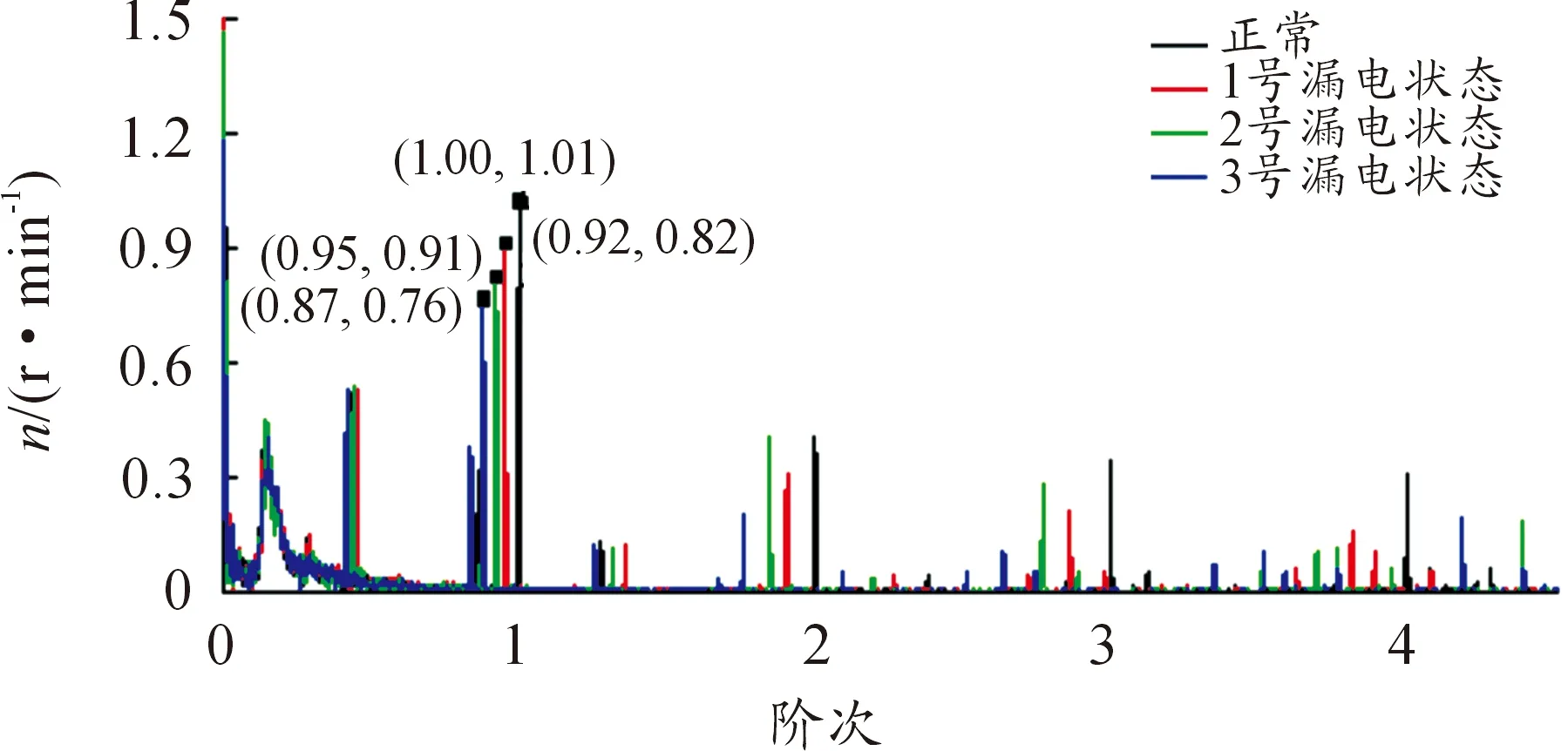
图13 正常和漏电状态下阶次谱
从图13可看到:相比正常转速在1阶及其2、3、4倍频处的阶次特征,轮毂电机3种不同程度漏电故障状态下的阶次特征均有变化。值得一提的是,由于实验中编码器安装并不能保证完全对中,3种故障状态均在靠近0.5阶处有1个阶次特征且存在该阶次的2、3倍频,该特征阶次并不随故障特征的改变而发生变化,因此该特征阶次表征为编码器安装误差的体现。由图中标出阶数可以看到:3种漏电状态下故障阶次特征分别减小0.130阶、0.008阶、0.005阶,可以判断,随着二极管个数增加故障阶次呈递减趋势。因此,通过阶次自分离方法可达到对轮毂电机漏电故障的故障类型及程度的识别和判断。
4 结束语
本文提出的阶次自分离方法以转速信号为监测对象,对蕴含在转速信号中的故障信息进行提取与分析,拓展了传统阶次跟踪技术的应用范围。基于含多矩形波故障的仿真信号对阶次自分离算法可行性进行验证,仿真分析结果表明:所提阶次自分离方法可以识别故障信号的阶次。同时,以轮毂电机为实验对象,利用阶次自分离方法对其漏电故障进行诊断,实验结果进一步表明:阶次自分离方法可提取出蕴含在轮毂电机输出转速中的非正常波动成分的阶次特征,且随着漏电故障支路上二极管导通个数的增加,即漏电故障程度的递减,转速故障信号的阶次特征逐渐减小。因此,阶次自分离方法可较好地从转速信号中提取表征轮毂电机漏电故障状态的特征,这对轮毂电机的故障诊断理论研究具有一定的参考价值。该方法也可以拓展到其他类型旋转机械的故障诊断中。
参考文献:
[1]CHAN C C.The state of the art of electric and hybird vehicles[J].Proceedings of IEEE,2002,90(2):247-253.
[2]宋宝玉,解志杰,张锋,等.基于角度域同步平均和阶次分析的低速斜齿轮故障诊断[J].吉林大学学报(工学版),2015,45(2):454-459.
[3]陈向民,于德介,李蓉.基于形态分量分析与阶次跟踪的齿轮箱复合故障诊断方法[J].航空动力学报,2014,29(1):225-232.
[4]BORGHESANI P,PENNACCHI P,CHATTERTON S,et al.The velocity synchronous discrete Fourier transform for order tracking in the field of rotating machinery[J].Mechanical Systems and Signal Processing,2014,44(2):118-133.
[5]SAPENA-BANO A,PINEDA-SANCHEZ M,PUCHE-PANADERO R,et al.Harmonic Order Tracking Analysis:A Novel Method for Fault Diagnosis in Induction Machines[J].IEEE Transactions on Energy Conversion,2015; 30(3):1-9.
[6]王况,王科盛,左明健,等.基于阶次分析技术的行星齿轮箱非平稳振动信号分析[J].振动与冲击,2016,35(5):140-145.
[7]王贞云,刘永强,廖英英.基于阶次分析的变转速滚动轴承故障诊断[J].汽车工程师,2016(7):46-50.
[8]朱茂桃,徐 祥,田 园.动力分流混合动力变速箱噪声源阶次分析研究[J].机械设计与制造,2014(3):220-223.
[9]ALWODAI A,YUAN X,SHAO Y,et al.Modulation signal bispectrum analysis of motor current signals for stator fault diagnosis[J].IEEE International Conference on Automation and Computing,2012(5):1-6.
[10] AKAR M.Detection of a static eccentricity fault in a closed loop driven induction motor by using the angular domain order tracking analysis method[J].Mechanical Systems and Signal Processing,2013,34(1/2):173-182.
[11] 王海童.阶次分析在1.5 MW风电增速箱故障诊断中的应用研究[M].沈阳:沈阳工业大学,2016.
[12] 于钟深,方向,张卫平,等.基于平滑先验法的被动声信号趋势项消除[J].探测与控制学报,2015(4):34-36.
[13] 何鹏举,冯亮.加速度信号随机噪声及趋势项实时消除方法研究[J].电子设计工程,2013,21(14):18-22.
