特殊线性方程组的求解

罗美金，林远华，欧阳云，覃炜达

（河池学院　数学与统计学院，广西　宜州　546300）

在高等数学、线性代数中，求解线性方程组对于大多数人并不陌生，从简单的一元方程到二元方程组以及多元方程组，在各个领域中都具有广泛的应用.线性方程组的形式多样，未知数个数可以大于、等于或小于方程组个数，解的形式也有无穷多解、唯一解和无解的情形.本文以含有n个未知数x1,x2,…,xn的n个线性方程的方程组（1）为例，只讨论具有唯一解的情形.

结合矩阵的基本运算，可将任意的线性方程组表示成Ax=b，其中A,b分别为线性方程组的系数矩阵和等式右端的常数项.因此，（1）式可利用矩阵表示为：

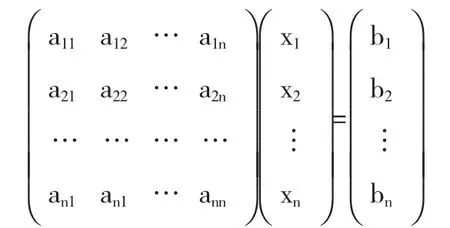
不妨假设n=3，以下线性方程组（2）为例，并分别利用行列式、矩阵初等变换、逆矩阵求解.

1　利用行列式求解方程组

含有n个未知数n个线性方程的Ax=b，若系数行列式|A|≠0时，则可借用克莱姆（Cramer）法则求解，这时所得方程组具有唯一解，且其中 |Ai|是 b1,b2,…,bn对应替换|A|中第i列的元素a1i,a2i,…,ani所得的行列式[1-3].

分析：利用克莱姆法则求解线性方程组，必须要满足两个条件：①方程个数等于未知数个数；②系数行列式不等于0.

解计算线性方程组（2）的系数行列式

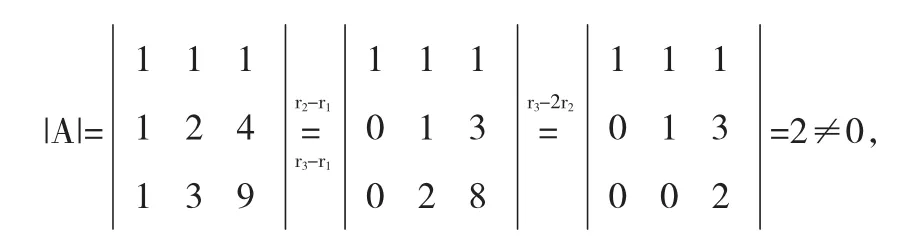
同理，可求得|A1|=4，|A2|=1，|A3|=1.根据克莱姆法则可得，此时方程组具有唯一解，且

2　利用矩阵的初等变换求解方程组

众所周知，求解线性方程组最直接方法的是消元法.矩阵初等变换求解方程组过程类似于消元法，所不同的是矩阵初等变化是消元法的简化，方程组在变换过程中实际上发生改变的只有A和b.因此，利用矩阵的初等变换求解方程组只需将(A,b)（(A,b)为系数矩阵A的增广矩阵）化简为行阶梯形矩阵或行最简形矩阵，再还原成方程组解出即可.

非零矩阵为行阶梯形矩阵若满足[1-2]：①非零行在零行的上面；②非零行的首零元所在列在上一行的首非零元所在列的右面.非零矩阵为行最简形矩阵若满足[1-2]：①是行阶梯形矩阵；②非零行的首非零元为1；③首非零元所在的列的其他元均为0.

分析：利用矩阵初等变换，将线性方程组（2）的增广矩阵(A,b)化简为行阶梯形矩阵或行最简形矩阵.

3　利用逆矩阵求解方程组

若系数矩阵的行列式|A|≠0，则A可逆，记为A-1[1-2].因此，要求解方程组Ax=b，在方程组等式左右两端左乘A-1，则可得x=A-1b.

求解逆矩阵A-1，可利用为矩阵A的伴随

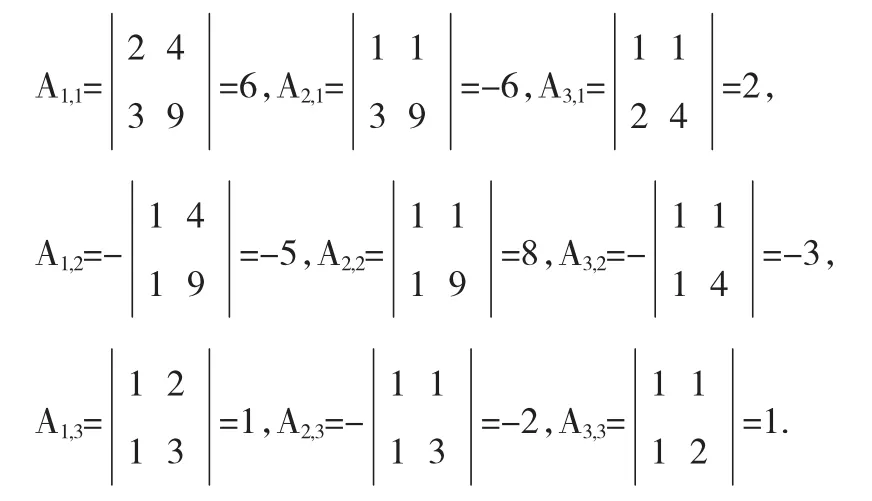
所以，

综上，利用行列式、矩阵初等变换、逆矩阵三种方法求解含有n个未知数x1,x2,…,xn的n个线性方程的方程组，三种方法各有优势，其中利用行列式、逆矩阵求解时比较适用于n≤3时，且需熟悉行列式的计算、代数余子式的计算；利用矩阵初等变换求解方程组的适用范围更广，尤其是n值较大时，则优先使用此方法.此外，也可借用数学工具matlab、maple等来计算.掌握线性方程组的求解对于学好数学类基础课程具有重要的作用，从而为各专业的后继课程的学习奠定了基础.

参考文献：

〔1〕同济大学数学系.工程数学线性代数[M].北京：高等教育出版社，2005.

〔2〕周勇，朱砾.线性代数[M].上海：复旦大学出版社，2009.

〔3〕同济大学数学系.高等数学[M].北京：高等教育出版社，2004.