最大模原理的推广及其应用
2018-04-03阮世华宋丽平
阮世华,宋丽平
(莆田学院 数学与金融学院,福建 莆田 351100)
最大模原理是解析函数特有的性质.最大模最小模原理是解析函数论中最有用的定理之一,具有许多重要的应用.
1 单复变函数的最大模、最小模原理及其推论
定理1(最大模原理[1])设函数f(z)在区域D内解析,则|f(z)|在D内任何点都不能达到最大值,除非在D内f(z)恒等于常数.
最大模原理说明了解析函数在区域边界上的最大模可以限制区域内的最大模.则也是解析函数特有的性质.
由此原理我们不难得出下面几个推论:
推论1[1]设(1)函数f(z)在有界区域D内解析,在闭区域=D+∂D上连续;
则除 f(z)为常数的情形外,|f(z)|<M(z∈D).
推论2(最小模原理[1])若区域D内不恒为常数的解析函数f(z),在D内的点z0有f(z0)≠0,则|f(z0)|不可能是|f(z)|在D内的最小值.
那么对应的最小模原理的推论:
推论3[1]设(1)函数f(z)在有界区域D内解析,在有界闭区域=D+∂D上连续;
(2)f(z)≠0(z∈D);
(3)存在 m>0 使 |f(z)|≥M(z∈D),则除 f(z)为常数外,|f(z)|>m(z∈D).
推论 4设(1)函数 f(z)在区域 D 内解析,(2)f(z)≠0(z∈D);则除f(z)为常数外,|f(z)在D内既不能达到最大值,也不能达到最小值.
2 多元复变函数的最大模、最小模原理及其推论
我们分别用Cn和Rn表示n个复变数和实变数的空间,Cn=Rn+iRn,Rn空间中的点用 x=(x1,x2,…,xn),y 等表示,Cn空间中相应的点用 z=(z1,z2,…,zn)=x+iy,ζ,…表示.
定义1[2]函数f(z)称为在点z0∈Cn全纯,如果在这点的某一个邻域存在所有一阶偏导数,α=1,2,…,n.即如果满足Cauchy-Riemann条件,α=1,2,…,n.
其中 f=u+ivn,zα=xα+iyα.
因此,函数f(z)在Riemann意义下在z0∈Cn全纯,如果它在这点的某一邻域分别对每一个变量全纯(当固定其余变量时).
定理2[2]若f(z)在域D⊂Cn全纯,在D中一非空开子集上为零,则f(z)在D恒等于零.
定理3(最大模原理[2])如果f(z1,z2,…,zn)在区域D⊂Cn内全纯,在闭区域=D+∂D上连续,则除了f(z1,z2,…,zn)为常数的情形外,那么|f(z1,z2,…,zn)|只能在D的边界上取最大值.
证明实际上只要证明,如果|f(z)|在D内的一点a=(a1,a2,…,an)达到其极大值,则f(z)在D内为常数.根据定理2,只需证明f(z)在一包含于D的多圆柱Dn(a,r)为常数即可.设b=(b1,b2,…,bn)为 Dn(a,r)的任一点,据假设,|f(a1,an-1,…,an)|≥|f(a1,an-1,…,an)|,当 |zn-an|<rn.应用单复变函数的最大模原理知,f(a1,an-1,…,an)为常数,故有 f(a1,an-1,…,an)=f(a1,…,an-1,bn).再应用最大模原理于单复变数函数f(a1,an-2,…,zn-1,bn),可知f(a1,…,an-2,bn-1,bn)=f(a1,…,an-2,an-1,bn).如此继续,最后得出 f(a1,…,an-1,an)=f(b1,…,bn-1,bn),故 f(z)在 Dn(a,r)为常数.
同样的,我们可以由这个最大模原理推出对应的最小模原理.
定理4(最小模原理) 若区域D⊂Cn内不恒为常数的全纯函数f(z),在D内的点 z0有f(z0)≠0,则|f(z0)|不可能是|f(z0)|在D内的最小值.
证明(反证法)假设|f(z0)|是|f(z)|在D内的最小值.因为f(z0)≠0,所以f(z)在D⊂Cn为恒不为零.则是在内的最大值,且在D内全纯.则由最大模原理在D内恒为常数.所以假设不成立,所以|f(z0)|不可能是|f(z)|在D内的最小值.
则有下面的推论
推论5设(1)函数f(z)在有界区域D⊂Cn内全纯,在有界闭区域=D+∂D上连续;
(2)f(z)≠0(z∈D);
则除 f(z)为常数外,|f(z)|>m(z∈D).
定义 2[2]设 Dα为 zα(α=1,2,…,n)平面的有界区域,当 z1,z2,…,zn彼此无关地分别在D1,D2,…,Dn上变动时,复数组(z1,z2,…,zn)的全体所构成的Cn中的区域,称为广义多圆柱区域,以(D1,D2,…,Dn)表示之,即(D1,D2,…,Dn)=D1×D2×…×Dn.
这时D=D1×D2×…×Dn的整个边界∂D由以下的点组成
zα∈∂Dα,(z1, …,zα-1,zα+1, …,zn)∈1×…α-1×α+1…×n,α=1,2,…,n.
而 n 维可定向的曲面 τ=∂D1×∂D2×…×∂Dn称为广义多圆柱域的特征流形,它是D域的边界上的一部分.
特别的,有下面的结论
定理5[2]若函数f(z)在广义多圆柱域D=D1×D2×…×Dn上全纯,且在仍然连续,则|f(z)|在D的特征流形上达到其最大值.
类似的,我们可以得到下面结论
定理6若(1)在广义多圆柱域D=D1×D2×…×Dn上不恒为常数的全纯函数f(z),且在仍然连续;
(2)f(z)≠0(z∈D);
则|f(z)在D的特征流形上达到其最小值.
3 应用
3.1 证明调和函数的极值原理
定理7[3]一个在区域D内不为常数的调和函数,不可能在这区域的内点达到最大值或最小值.
证明假定调和函数u(z)不为常数,且在区域D的内点z0处达到最大值.设圆盘 |z-z0|<ρ(0<ρ<+∞)在区域 D 内.做出在|z-z0|<ρ内解析的函数 f(z),使其实部为 u(z).显然,f(z)不为常数.于是在|z-z0|<ρ解析的函数ef(z)(不为常数)的模在z0达到最大值eu(z0),与最大模原理相矛盾.因此u(z)在z0不可能达到最大值.考虑函数e-f(z),可以证明u(z)在区域D内一点也不可能达到最小值.
注:类似的,我们可得到次调和函数也是满足极大值原理[2].但由于多于一个复变量时调和函数和全纯函数的实部不是等价的,因此我们就不涉及这方面的问题.
而关于单复变量的最值原理的应用还有很多方面[4-8],比如利用它证明代数学基本定理、证明函数有零点存在、证明函数为常数、证明函数为分式线性函数等等.已经有很多的文章做了非常详细的证明,在此就不再详述.
下面我们看一个多复变量最值的应用.
3.2 证明Cn中全纯域的圆盘性质
复数平面C1上任一开集都是全纯域,但在Cn中并非如此的.特别的,单位圆盘在复数平面上是很有代表性的区域,它的重要性质就是它是一个全纯域.下面我们来看一下Cn中的全纯域的圆盘性质.
定义3[2]我们称Cn中的域D具有圆盘性质,如果对C1中的圆盘Δ,存在一簇映射
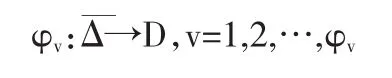
定理8[2]若D⊂Cn为全纯域,则D具有圆盘性质.
证明设 {φv}为圆盘性质定义中的一簇映射,取K=设D为全纯域,因而全纯凸.则对任何f∈A(D),z∈φv(Δ),由极大值原理可知
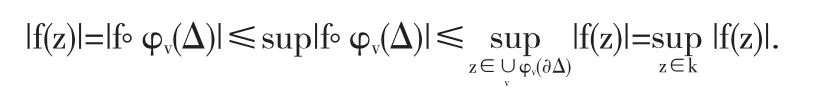
参考文献:
〔1〕钟玉泉.复变函数论[M].北京:高等教育出版社,2013.
〔2〕钟同德,黄沙.多元复分析[M].河北:河北教育出版社,1990.
〔3〕余家荣.复变函数[M].北京:高等教育出版社,2014.
〔4〕朱丽芹.最小模原理的证明[J].济南大学学报(自然科学版),2009,23(3):315-316.
〔5〕袁邢华,吕效国,李磊.最大模原理及其应用[J].高师理科学刊,2011,31(5):5-6.
〔6〕彭小智,凌能祥.相依样本下回归函数分割估计的渐近正态性[J].南通大学学报(自然科学版),2009,8(4):89-94.
〔7〕李云霞.最大模原理的推广[J].数学的实践与认识,2000,30(2):153-155.
〔8〕陈继理.复函数在代数基本定理证明中的应用[J].杭州师范学院学报,2004,3(3):277-278.
