Maple软件在高等代数课程中的应用探索
2018-04-03刘秀英孔祥强
刘秀英,孔祥强
(菏泽学院 数学系,山东 菏泽 274015)
Maple、Mathematica和MATLAB是数学类的三大软件.Maple软件是由加拿大滑铁卢大学和Waterloo Maple Software公司注册的一套为微积分、代数学和微分方程等使用的数学软件[1].Maple软件不仅具有很好的符号运算功能,而且具有强大的数值计算功能和动态处理图形的功能[2].在数学的很多分支中有着广泛的应用[3,4,5,6].
高等代数课程内容比较深奥、抽象,证明过程比较繁琐、难懂,针对课程的这些特点,引入Maple软件,可很好的帮助解决这些问题.数学软件与传统教学方式相结合,可大大提高学习的积极性,增强学习的趣味性,达到提高学习效率和教学质量的目的,为进一步学习其他专业课打下坚实的基础.
1 Maple软件在多项式计算中的应用
高等代数中有关多项式的内容,主要包括多项式整除、因式分解定理、多项式函数及多元多项式等.最大公因式部分是多项式整除中的重要内容,主要是用辗转相除法求多项式的最大公因式,而当多项式的系数不是整数时,该法计算起来非常复杂,极易出错.为了实现计算迅速且结果准确的目标,不妨借助Maple软件编程,可达到事半功倍的效果.
案例1设多项式求(f(x),g(x)),并求 u(x),v(x),使得(f(x),g(x))=u(x)f(x)+v(x)g(x).
利用Maple软件编程可轻松实现这一过程,避免了用辗转相除法进行复杂、繁琐的计算.

s,t
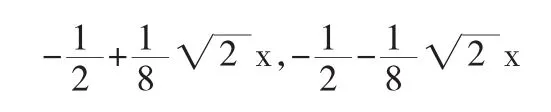
准确地计算出多项式的最大公因式,是学好多项式中其他内容的基础[7].
2 Maple软件在矩阵计算中的应用
有关矩阵计算方面的内容非常丰富,主要包括矩阵的加法、减法、乘法、乘方;矩阵的三种初等变换;矩阵的转置;矩阵的秩;方阵的行列式计算;矩阵的特征值和特征向量;逆矩阵及伴随矩阵的求法等.以下通过实际数例,说明Maple软件的具体应用.
案例2设矩阵A=
通过Maple编程,实现矩阵高次方的计算.
with(LinearAlgebra):
A:=Matrix([[1],[0,-2,0,0],[0,0,-3,0],[0,0,0,-4]]):
MatrixPower(A,5)
MatrixPower(A,6)
MatrixPower(A,n)
wuth(linlg):
L:=matrix(4,4,[0,0,1,-1,0,3,1,4,2,7,6,-1,1,2,2,-1]):
adj(L)
程序输出的结果为A5=
矩阵可以看作学好高等代数课程的重要工具,而矩阵的计算是必须熟练掌握的内容.以Maple软件为依托,使得计算简单易行.通过软件,也可动态的实现每一步的计算过程,可以通过修改参数,讨论不同的情形,从而更深刻地掌握知识点.
案例3判断矩阵A=是否相似?矩阵C=是否相似?
通过调用软件包with(linalg)语句,编程
with(linalg):
A:=matrix(3,3,[2,-1,-1,-1,2,-1,-1,-1,2])
B:=matrix(3,3,[1,0,0,0,1,0,0,0,0])
issimilar(A,B)
false
with(linalg):
C:=matrix(3,3,[1,0,1,0,3,0,1,0,1])
H:=matrix(3,3,[2,0,0,0,3,0,0,0,0])
issimilar(C,H)
trie
由输出的结果知,A和B不相似;C和H相似.
案例4求矩阵的特征值和
特征向量.
利用Maple软件编程,
with(linalg):
A:=matrix([[5,-2,-4,3],[3,-1,-3,2],[-3,,,-],[-10,3,11,-7]]])
E:=array(1..4,1..4,identity):
et(matadd(evalm(lambda·E),-A)):
f:=lambda→λ4-λ3+λ32:
linsolve(matadd(evalm(0·E),-A),vector([0,0,0,0]))[2_t1-_t23_t1-t2_t1_t2]
linsolve(matadd(evalm(1·E),-A),vector([0,0,0,0]))[3_t1_t1_t1-2_t1]
linsolve(matadd(evalm(1·E),-A),vector([0,0,0,0]))2[-4_t1-2_t1_t16_t1]
3 Maple软件在解线性方程组中的应用
线性方程组的求解是高等代数中的重要内容.设方程组系数矩阵的秩为R(A),增广矩阵的秩为R(AMd),方程组中未知量的个数为n,则(1)当R(A)=R(AMd)时,方程组有解.若R(A)=R(AMd)=n,则方程组有唯一的解;若 R(A)=R(AMd)<n,则方程组有无穷多组解.(2)当R(A)≠R(AMd)时,方程组无解.判断矩阵的秩,一般是先把矩阵化为行阶梯形;而为了求方程组的解,一般需化到行最简阶梯形,这样方便求解.利用Maple软件,通过实际例子进行说明.
案例5将矩阵A=及矩阵B=化为行最简阶梯形.
利用Maple软件编程,
with(student[LinearAlgebra]):
A:=〈〈0,-3,3,6〉|〈1,2,-3,-9〉|〈3,7,2,1〉|〈-6,9,3,0〉〉:
b:=〈0,1,2,-3〉:
GaussianElimination(A):
ReducedRowEchelonForm(〈A〉)
ReducedRowEchelonForm(〈B〉)
有了行阶梯形作为铺垫,求方程组的解就容易多了.
案例6解线性方程组
Maple程序
with(linalg):
A:=matrix(5,5,[1,3,5,-4,0,1,3,2,-2,1,1,-2,1,-1,-1,1,-4,1,1,-1,1,2,1,-1,1]):
b:=matrix(5,1,[1,-1,3,3,-1]):
B:=augment(A,b):
gaussjord(B);
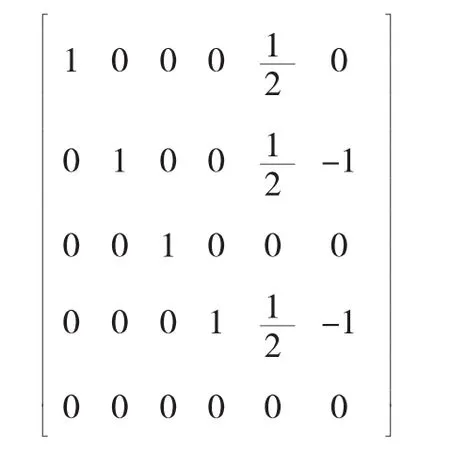
solutions:=backsub(%);
由输出的结果知,R(A)=R(A,b)=4,n=5,所以方程组有无穷多组解,其通解为其中k为任意常数.利用类似的编程方法,还可判断出线性方程组有唯一解和无解的情形.
4 结束语
本文通过具体的数学实例,探讨了Maple软件在高等代数课程中的应用.实际上,代数中的很多问题都可以通过编程实现.将数学软件引入课堂,可大大提高学生学习的积极性,
增强数学的趣味性,实现复杂内容的简单化、抽象问题的具体化.打好了基础,才能更深入地学习其他的数学知识.利用Maple软件提供的软件包,可以帮助实现做题过程的动态化展示,从而更深刻地理解解题思路和方法.
参考文献:
〔1〕李锐,程美玉,张伟.Maple软件在线性代数与解析几何学习中的应用[J].实践探索,2016(9):77-78.
〔2〕张晓丹,堵秀凤,李祥林,张永胜,张永春.Maple 的图形动画技术[M].北京:北京航空航天大学出版社,2005.
〔3〕阿荣.Maple在线性代数教学中的应用[J].高等数学研究,2013,16(4):97-99.
〔4〕李姝妹.数学软件Maple在常微分方程教学中的应用[J].阴山学刊,2013,27(4):55-57.
〔5〕吴珞.Maple和Maple T.A.在大学数学教学中的应用[J].上海第二工业大学学报,2013,30(2):130-134.
〔6〕孔祥强.Maple在高等数学教学中的应用探索[J].钦州学院学报,2016,31(1):54-57.
〔7〕李治强,梁燕来,胡源艳,易亚钊.Maple在高等代数实验教学中的应用探索——以一种多项式因式分解方法为例[J].玉林师范学院学报,2011,32(5):32-36.
