一类非线性椭圆方程解的存在性
2018-04-03陈俊龙杨柳青柴晓娟
陈俊龙,杨柳青,柴晓娟
(安徽大学 数学科学学院,安徽 合肥 230601)
1 引言
设Ω是RN(N≥2)上一个有界光滑区域,本文研究如下带低正则值和退化耗散系数的非线性椭圆方程解的存在性,
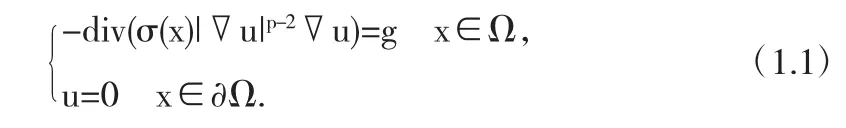
其中,g∈L1(Ω),p∈(1,N),耗散系数 σ(x)非负、有界可测,在区域Ω内部至多有限个零点并且满足如下假设:
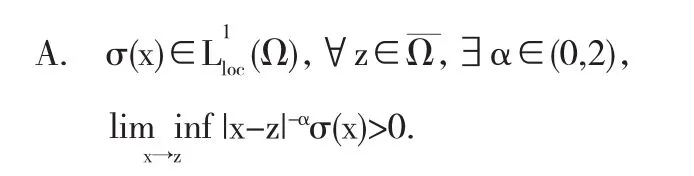
带低正则值得椭圆方程解的存在性问题一直偏微分方程领域比较热点的问题.自上世纪七十年代以来,Stampacchia、Benilan、Brezis等学者对外力项为可积函数或一般Radon测度的线性或半线性椭圆方程界的存在性问题进行了深入研究[1-4].近年来,围绕带低正则值的椭圆、抛物方程解的存在性问题产生了大批新的结果,参见[5,6,7]及本文第三作者的工作[8].
带有退化耗散系数的椭圆或抛物方程主要产生于非均匀介质中扩散现象的描述.在文献[9]中,Cardiroli等学者研究了g∈L2(Ω)时上述方程弱解的存在性.本文借助文献[3,4]的思想,研究g∈L1(Ω)时上述方程解存在性问题.
2 预备知识和主要结果
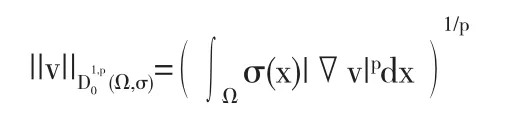
定义2.1我们称v∈T10,1(Ω,σ)是方程(1.1)的熵解.如果∀k>0,Tk(v)∈W10,p(Ω),且对任意的 φ∈D10,p(Ω,σ)∩L∞(Ω),有
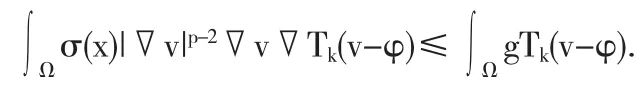
定理 2.2设g∈L1(Ω),σ(x)非负、有界可测,在区域Ω内部至多有限个零点且满足条件A,则问题(1.1)至少有一个熵解.
3 定理证明
设{gn}是光滑的函数列,在L1(Ω)中收敛于g,且满足||gn||L1(Ω)≤||g||L1(Ω).考虑如下逼近方程
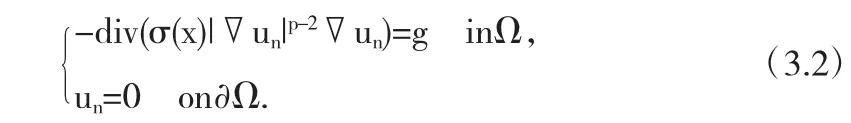
由经典的椭圆方程解的存在性结果可知,对于任意给定的 n,方程(3.2)至少有一个解 un∈D10,p(Ω,σ).下面我们建立un的一致估计,进而给出原方程解的存在性.令q∈[1,Np/(N+α)),由(3.2)及 Holder不等式可得
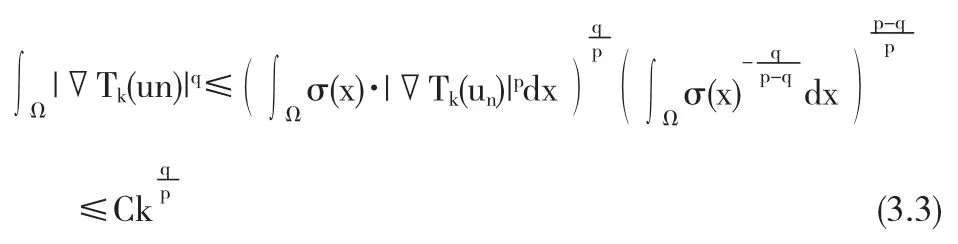
记 q*=Nq/N-q,则∀0<ξ≤k,
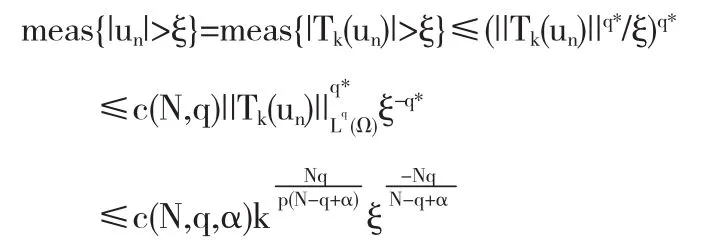
取 ξ=k,则∀s<Nq/(2N-2q+2α)(>1),
由(3.3)及 Sobolev嵌入定理知{Tk(un)}是L1(Ω)中的柯西列,因此也是测度意义下的柯西列.由于∀δ>0,
meas{|un-um|>δ}≤meas{|un|>k}+meas{|um|>k}+meas{|Tk(un)-Tk(um)|>δ}.
结合(3.5)知{un}是以测度意义下的柯西列.不妨假设其依测度收敛于函数u.下面证明{▽un}在测度μ=σdx下是依测度柯西列.∀δ>0,
meas{σ|▽un-▽um|>δ}≤meas{|un-um|>η}+meas{|un-um|≤η,σ|▽un-▽um|>δ}≐E1+E2
由于{un}是以测度柯西列,当η充分小时,有E1<ε.另一方面,
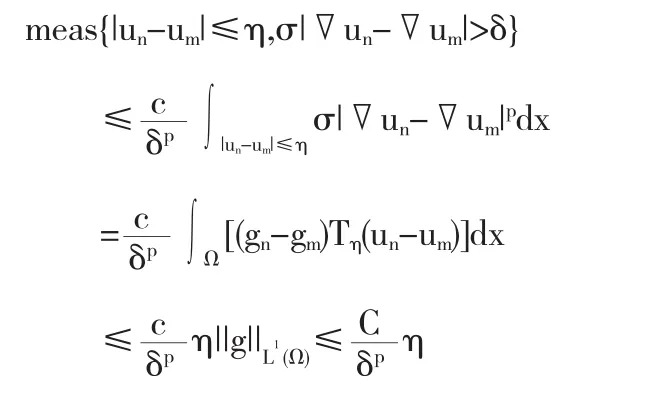
当 η 充分小时,有 E2<ε.因此{▽un}在测度 μ=σdx 下是依测度柯西列,且其极限为▽u.取Tk(un-φ)作为试验函数,其中φ∈D10,p(Ω,σ)∩L∞(Ω),则由(3.2)得
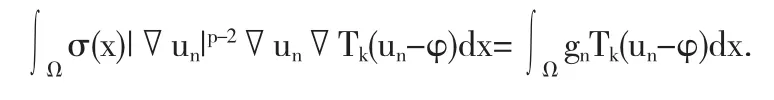
显然∫Ωgn·Tk(un-φ)dx→∫Ωg·Tk(un-φ)dx.进一步,由于Tk(un-φ)dx在 D10,p(Ω,σ)中弱收敛到 Tk(un-φ),根据 Fatou 引理可推出
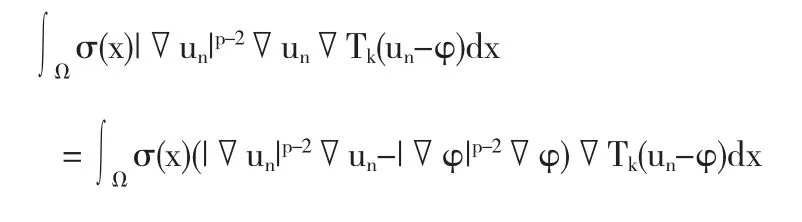
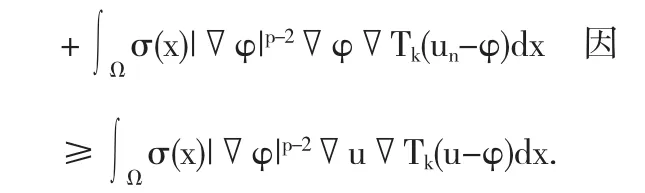
因此u是问题(1.1)的熵解.证毕.
参考文献:
〔1〕G.Stampacchia,Equations elliptiques du second ordre a coefficients discontinus,Presses de l’Universite de Montreal,1966.
〔2〕Ph.Benilan,H.Brezis,Nonlinear problems related to the Thomas-Fermi equation,J.Evolution Equations 3(2004)673–770.
〔3〕L.Boccardo,T.Gallou?t,Nonlinearellipticand parabolicequationsinvolvingmeasuredata,J.Funct.Anal.87(1989)149–169.
〔4〕Ph.Benilan,L.Boccardo,Th.Gallouet,R.Gariepy,M.Pierre,J.L.Vazquez,An L 1-theory of existence and uniqueness of solutions of nonlinear elliptic equations,Ann.Sc.Norm.Super Pisa Cl.Sci.22(4)(1995)51–273.
〔5〕H.Brezis,M.Marcus,A.C.Ponce,Nonlinear elliptic equations with measures revisited.Mathematical aspects of nonlinear dispersive equations,55--109,Ann.of Math.Stud.,163,Princeton Univ.Press,Princeton,NJ,2007.
〔6〕L.Boccardo,L.Moreno-Mérida,solutions of nonlinearproblemswithnonhomogeneousNeumann boundary conditions.Milan J.Math.83(2015),no.2,279–293.
〔7〕L.Francesco,R.Eugénio,S.Vasile Quasilinear elliptic systems with measure data.Nonlinear Anal.154(2017),210–224.
〔8〕X.Chai,W.Niu,Existence and non-existence results for nonlinear elliptic equations with nonstandard growth.J.Math.Anal.Appl.412(2014)1045–1057.
〔9〕P.Cardiroli,R.Musina,On a variational degenerate elliptic problem,NoDEA Nonlinear Differential Equations Appl.7(2000)47–199.
