永磁电机气隙磁场计算比较研究∗

武红斌 王柯人

1 引言

随着永磁材料以及计算机技术的发展和应用，电机的结构及设计出现了许多新的变化。由于永磁电机不需要外部励磁就能建立磁场，因此可使电机结构简单，尺寸减小，可靠性及效率提高。特别是稀土永磁材料，给永磁电机提供了更广泛的发展前景。然而，新材料的使用迫切需要有新的理论和方法去指导实际的电机设计。

永磁电机气隙磁场的分布是永磁电机设计的基本问题［1］。永磁电机的力矩及脉动情况等为设计者所关注的问题，都与电机气隙磁密波形的准确计算有密切的关系。目前，对于永磁电机气隙磁场分析和计算，学者们提出了很多种方法。这些方法大致可以分为有限元数值法和解析法两类，都基于一定的简化和假设，有着各自的使用范围和优缺点。

有限元数值分析法能够准确地计算气隙磁场，但在电机的优化设计中并不方便。解析法虽然精度稍差，但能准确表述影响磁场分布的参数，可以直观地调整参数，进行优化。

2 有限元分析法

永磁电机采用永磁体励磁，电机内部的电磁场分布较为复杂，采用传统的等效磁路方法分析一般比较复杂，而且可能会带来较大的误差，为保证计算的准确性，一般采用有限元法对电机内部电磁场进行数值计算。

2.1 编程进行有限元法数值分析［2］

有限元分析时的假设：

1）磁场沿轴向不变，因此可作为二维磁场处理。

2）磁场仅被限制在电机的内部，定子外部边界是零矢量磁位线，即Az=0。

3）电机的铁心磁导率各向同性。

电磁场有限元模型采用有限元法对同步电动机空载磁场进行分析，首先应建立永磁体的数学模型，将永磁体的作用模拟为面电流的作用，其值为：Jm=Hc=νBr

式中Hc为磁体矫顽力，Br为剩余磁密，ν为磁体磁化方向的磁阻率。

建立电机应满足的准泊松方程的边值问题为

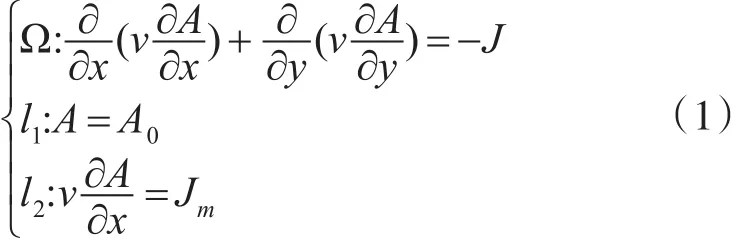
该方程等价于下面的条件变分问题：

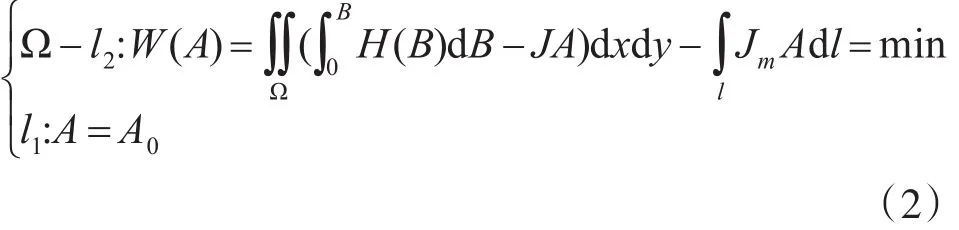
然后，可采用加权余量法、加辽金法等方法求解以上变分问题。

从以上分析可见，应用有限元法进行数值分析，需对有限元法熟练掌握，编制计算程序，工作繁琐且精度不高，后处理能力有限。

2.2 通过ANSYS软件进行有限元分析

ANSYS是目前应用最为广泛、使用最方便的通用有限元分析软件之一，该软件融结构、热、电磁、流体、声学于一体，能进行多物理场耦合计算，并具有极为强大的前、后处理功能。

在使用时，以有限元数值分析法为基础，按要求输入所要计算问题的结构和参数，通过计算机计算，便可获得结果，并可对结果进行进一步的开发使用，而不需要了解求解的详细过程，更不需要掌握有关技巧和编制任何程序，极大地方便了使用，节省了时间和精力。一般采用ANSYS软件进行有限元分析步骤如表1所示。

表1 用ANSYS软件对永磁电机进行有限元分析步骤［3］

用ANSYS对某高速永磁同步发电机内电磁场进行分析，过程及结果如下：

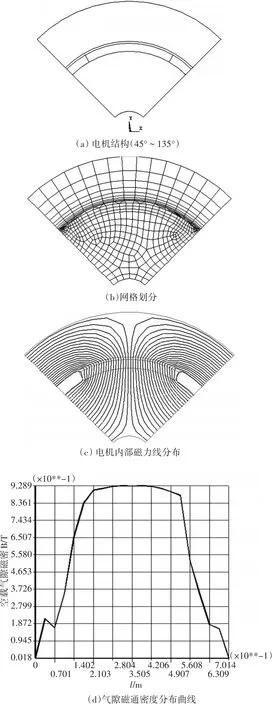
图1 用ANSYS对永磁同步发电机内电磁场进行分析的过程及结果

另外有一种等效磁网络法［4～6］实质上是简化的有限元方法，其突出的优点是网络中各单元的划分可形成规范化，前后处理工作量小，便于对不同磁路结构的电机进行计算。尤为重要的是，非线性的节点磁位方程阶数一般不超过100阶，同电磁场有限元分析相比，计算时间大为减少。其网络形成的依据是等效磁通管原理，即将电机中磁通分布较均匀而几何形状又比较规则的部分作为一个独立的单元，计算其等效磁导，这样的单元有很多，如：电机中定、转子各个齿部以及齿与齿之间的轭部都可作为独立的单元，各单元之间通过节点相连接。根据磁网络与电网络的相似性，由节点法或回路法即可求出各节点的磁位或通过各单元的磁通，进而求得电机的有关参数。

同有限元方法相比，等效磁网络法计算误差主要产生于：1）它不能精确表示出齿槽对气隙磁密分布的影响，计算的气隙磁密曲线显得粗糙。2）为了使等效磁导的划分与实际齿的各个部分饱和程度相同，必须对齿进行细分，等效为多个磁导。

3 解析方法

目前，学者们提出了许多种永磁电机气隙磁场的解析分析法，由于其基本假设的不同，通用性和适用的范围也不一样。在此，仅举一例作详细说明。

文献［7］提出了一种通用性较强的解析方法。为了简化分析，其基本假设为：1）两平行背铁沿x方向长度近似认为无穷大，磁导率认为是无穷大。2）磁极与背铁的深度（沿z方向）足够大。3）永磁电机的磁极材料选用稀土材料（如NdFeB）。将永磁磁极等效为一个集中线圈，位于定子表面，等效磁势为F0。永磁电机的基本模型和等效磁势F0沿空间分布如图2、图3所示。

图2 永磁电机的磁场计算模型

图3 永磁磁极磁势分布图

定子表面的磁势表达式为

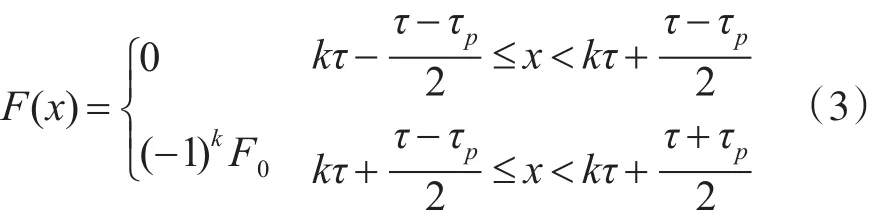
其中，τp为极宽，τ为极距，k=0，±1，±2，…。

将F(x)展开成傅立叶级数：

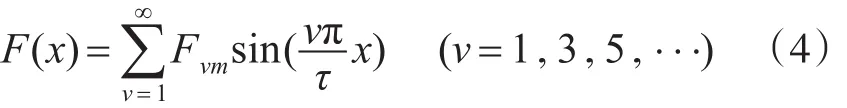
由于气隙中无电流分布，所以气隙磁场是无旋场。设气隙域中标量磁位为φm，则∇2φm(x，y)=0。整个问题为求解具有第一边值的拉普拉斯方程问题。

相应的边界条件为

1）y=δ时，φm(x，δ)=0

采用分离变量法［8］，可解得

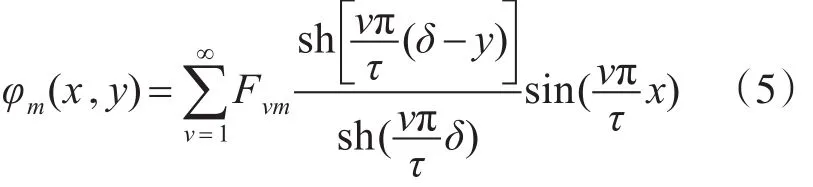
由 B=-μ0∇φm可解得

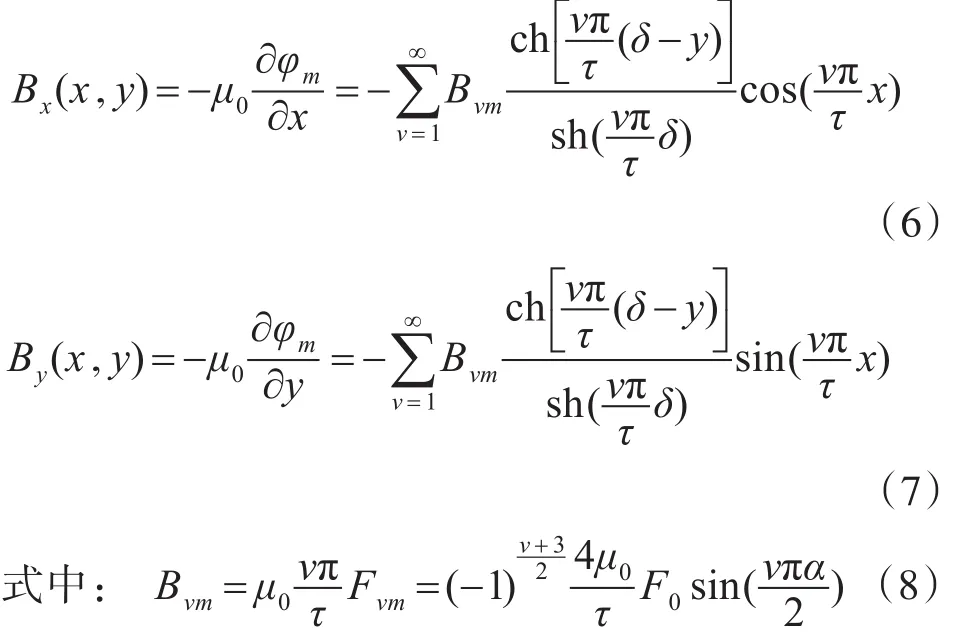
式（6），（7）给出了气隙中任意位置的磁通密度。形式上表现为各次谐波分量的和。

由以上方法可见，解析分析方法能准确表述影响磁场分布的参数，可以直观地调整参数，进行优化。

此外，文献［1］、［9］利用解析方法对气隙磁场进行计算，求解出气隙磁场的分布波形，文中忽略了齿槽的影响。文献［10］讨论了永磁电机中定子斜槽（或转子斜极）、永磁体磁化方式、气隙长度、转子半径和永磁体极弧系数对气隙磁场分布的影响，给出计算气隙磁场分布的经验公式，由此计算出相绕组反电动势变化波形，文中忽略了齿槽的影响，公式的通用性也较差。文献［11］采用等效磁路的方法构造出考虑齿槽效应的气隙磁导分布函数，以此求解电机内气隙磁场的分布，文中等效磁路法默认为齿槽效应对气隙磁场分布的影响程度与气隙内的径向位置无关，这与实际磁场分布有一定偏差［12］。文献［13］采用部分区域的方法，利用连续边界条件求解齿槽对气隙磁场的影响，文中忽略了永磁体相对磁导率μr的影响。

4 结语

在气隙磁场的求解方法中，有限元数值计算方法可以较准确计算出气隙磁场的分布波形，具有通用性强、适用于各种媒质的特点。但其对使用者有较高的要求，在电机优化设计中不直观，不便采用。解析方法可以较准确地计算气隙磁场分布波形，同时可以观察到气隙磁场分布与结构尺寸之间的关系，满足电机设计“准确和直观”的要求，具有很大的工程实用价值。学者们提出了多种解析方法，一般都基于一定的简化和假设，有着各自的使用范围和优缺点，在实际的电机设计中，可以根据具体要求，选择适当的方法。

［1］陈阳生，林友仰.永磁电机气隙磁密的分析计算［J］.中国电机工程学报.1994，14（5）：17-26.

［2］江辉，林荣文.基于有限元法和傅立叶变换求解稀土永磁同步电动机空载反电势［J］.中小型电机，2002，29（1）：16-18.

［3］吴海鹰.永磁电机电磁计算［J］. 船电技术，2004（5）：18-22.

［4］张伟雄.基于磁网络模型方波永磁电机气隙磁场的研究［J］. 微特电机，1999（6）：3-7.

［5］张伟雄，郑婵君，张敬华.基于等效磁网络模型的永磁电机气隙磁场的分析［J］. 中小型电机，2000，27（4）：12-18.

［6］梁华，李训铭，严登俊.稀土永磁同步电机优化设计分析［J］. 南京理工大学学报，2002，26（12）：138-143.

［7］秦世耀，熊光煜，牛华.永磁电机气隙磁场的解析分析［J］. 太原理工大学学报，2002，33（2）：121-124.

［8］汤蕴.电机内的电磁场［M］.北京：科学出版社，1981：54-56.

［9］N.Boules．Prediction of no-load flux density distribution in PM machines［J］.IEEE Trans.On Industrial Applica⁃tion，1985，21（4）：633-643.

［10］Sebastian T．Analysis of induced EMF waveforms and torque ripple in a brushless permanent magnet machine［J］.IEEE Trans.On Industry Appl． 1996，32（1）：195-200.

［11］Zhu Z Q，Howe D．Analytical prediction of the cogging torque in radial-field permanent magnet brushless motors［J］.IEEE Trans.On Magnetics，1992，28（2）：1371-1374.

［12］程福秀，林金铭.现代电机设计［M］.北京：机械工业出版社，1993：97-98.

［13］Q.Gu，H.Gao.Effect of slotting in PM electrical ma⁃chines［J］.Electrical Machines and Power Systems，1985，10（3）：273-284.