分形维数约束ICA-RLS的遥测振动信号降噪方法∗

玄志武 商诺诺 刘 学

1 引言

受试验环境、飞行器本身的振动和冲击以及测量传输等因素的影响，采集到的遥测振动信号夹杂着大量的高频、低频和冲击噪声、各阶次的谐波分量，频谱成分异常复杂。噪声的存在对于信号包络的有效提取是一种障碍，致使分解得到的包络信号变得不准确，对自适应时频分析技术的影响尤为明显，从而影响对信号进行进一步的时频处理。好的降噪效果对提高时频分析的分辨率、提高算法性能以及对信号特征的提取具有重要的实际价值和理论意义。

自适应降噪一直是信号处理领域研究的热点，如文献［1］提出利用样本熵方法对眼电信号中的伪迹成分进行自适应降噪，文献［2］提出采用模板匹配方法对眼电信号中的伪迹成分进行自动去除，且无需设置参考信号，但这两种方法需要根据先验信息或者历史经验去设定阈值，受人为因素影响较大。文献［3］提出直接利用RLS滤波器进行自适应滤波，但是RLS自适应滤波本质也是一种回归滤波方法，需要输入参考信号，因而它也回归滤波方法固有的“双边干扰”问题，且对遥测振动信号处理时，由于缺乏先验信息，很难确定参考信号。最近文献［4］提出一种独立分量分析（ICA）与递归式最小均方（RLS）相结合的ICA-RLS方法［4］对脑电噪声进行自适应降噪的方法，但是该方法是将ICA分解后的所有源信号进行滤波，很可能将部分信号当作噪声滤除，这对遥测振动信号处理是不可接受的，如果故障信息因滤波而损失或被滤除，将对试验的分析与鉴定产生严重影响。针对这一问题，本文提出一种基于分形维数约束的ICA-RLS的遥测振动信号降噪方法，首先提出基于峭度最大化的牛顿迭代ICA方法，对振动信号进行盲源分离；然后采用分形维数去筛选所需滤波的源信号，可以有效地避免把振动信号作为噪声被滤除；最后通过实际采集的遥测振动信号进行仿真验证，结果表明所提算法可以有效避免有用信息不受损失，且具有较好的降噪效果。

2 基于ICA的盲源分离方法

2.1 相空间重构

遥测振动信号通常采用单通道观测，其结果往往是一个矢量，如果想利用ICA盲源分离方法对单通道观测矢量数据进行处理，就需要进行相空间重构，本文采用混沌序列相空间重构的方法将振动信号扩展到多维相空间，使混叠的各源信号在多维空间中重新展开，然后采用ICA方法对源信号进行分离。

对遥测振动信号{x | xi， i=1，2，…，N}进行混沌相空间重构，得到 m维相空间{y | x1， x2+τ，…，xM+(m-1)τ} ，其中 m 和 τ分别为嵌入维数和延迟时间，M=N-(m-1)τ为相空间重构后的向量点数。相空间的重构质量与嵌入维数和延迟时间的选择有直接关系。由于对遥测振动信号缺乏先验信息，嵌入维数选取较为困难，可以先求延迟时间，根据延迟时间去确定嵌入维数，求取延迟时间的算法很多，如C-C算法［5-6］、G-P算法［6］、互信息量法［6］等，具体算法流程参见文献［5～6］，对比算法性能和计算效率，本文采用互信息量法获取延迟时间 τ，然后根据 τ和Takens原理［7］采用Cao算法［8］得到嵌入维数 m 。

2.2 基于峭度最大化牛顿迭代ICA算法

ICA是在统计独立性的假设下对混叠信号中的各独立源进行盲源分离的方法。即找到分离矩阵W，通过下式：

得到对源信号的估计 S^=[s^1，s^2，…s^M]T，进而达到盲源分离的效果，其中 S=[s1，s2，…sM]T为源信号矢量，A为混叠矩阵，X=[x1，x2，…xN]T为混叠信号矢量。由于传统的基于峭度的ICA方法采用不动点迭代法计算分离矩阵，存在计算效率低，分离矩阵不收敛，分离效果差等缺点。文献［9］采用牛顿迭代法来去获取分离矩阵W，但该方法存在当约束条件导致源信号的均值为零时致使算法不稳定的缺陷，针对这些问题，本文从峭度极大化的角度提出一种牛顿迭代的ICA方法，使用牛顿迭代法对峭度公式在约束条件的约束下对分离矩阵的迭代运算，在迭代的过程中通过降低分离结果的高斯性分离出各源信号，仿真实验表明该方法可以有效提高算法的运算效率和分离效果。

首先定义信号的峭度［9］

设s^=wTx，其中w为分离矩阵的W 的一个分量，则 kurt(s^)对 w 的梯度为［9］

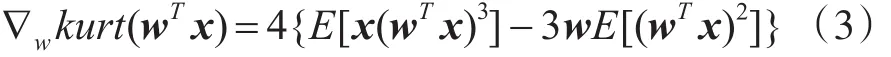
基于峭度最大化的目的，采用拉格朗日算法计算在约束条件E[(wTx)2]=||w ||=1下的极值解

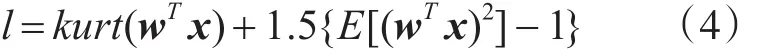
采用牛顿迭代法，得到w的迭代公式

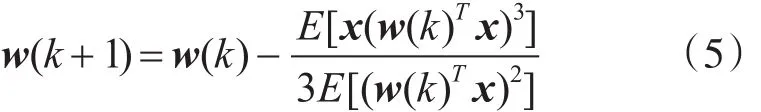
利用该迭代公式，当完成 p个独立分量的估计，为了防止各分量收敛到相同的极值点，本文采用去相关抽取法对每一次迭代后的线性组合进行去相关抽取，然后再进行归一化处理，这样就可以有效避免因约束条件使得各独立分量收敛到相同的极值点，导致源信号的均值为零致使算法不稳定的问题。具体公式如下：

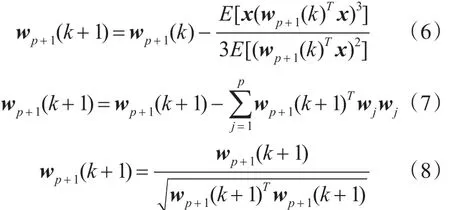
采用上面的方法对所有分量w进行估计后，就可以得到分离矩阵W。

3 分形维数约束ICA-RLS降噪方法

3.1 分形维数

分形理论作为一种重要的数学工具，可以对自然界中各种复杂的信号、形状和结构等进行定量描述，是当前信号处理领域研究的热点。本文采用分形维数对信号复杂度和不规则度进行度量。根据分形理论，分形维数大表明信号成份丰富且复杂，反之，表明信号简单且具有规律性。对于遥测振动信号处理而言，首要关心的是信号中的异常成份，通过异常频率去分析本身结构以及各系统是否出现异常，受试验环境、飞行器本身的振动和冲击以及测量传输等因素的影响，异常信号成份往往非常复杂，呈现较大的非线性和非平稳性，分形维数较大。通过大量试验分析，异常信号的分形维数（网格维数）大于1.5，这样就可以通过分形维数对ICA分离出的源信号进行筛选，对分形维数较大的予以保留，避免信息损失，对分形维数较小的源信号进行RLS滤波，达到降噪的目的。

3.2 网格维数与计算方法

分形维数又分为盒维数、关联维数、Hausdorff维数和网格维数等。对于一维信号来说盒维数与网格维数是等价的，本文采用网格维数更便于计算机处理。

给定遥测振动信号{x | xi， i=1，2，…，N}，其网格维数［10］定义为

3.3 分形维数约束ICA-RLS降噪方法

ICA-RLS降噪方法结合了盲源分离与自适应滤波算法的优点，采用ICA将混叠信号分解成源信号，再通过RLS自适应滤波对各独立源信号进行自适应滤波，在脑电信号降噪应用中取得了较好的效果，但在遥测振动信号应用中，由于该方法会对所有的源信号进行滤波，难免会造成信息损失，特别是将异常信号作为噪声滤除将大大减少该遥测信号的利用价值，对试验分析将产生严重影响，为了解决这一问题，本文采用分形维数去约束ICA-RLS滤波过程，避免有用信息的损失。算法流程如下：

1）对采集到的遥测振动信号进行预处理：零漂修正、趋势项消除，然后对其进行相空间重构；

2）采用基于峭度最大化牛顿迭代ICA算法对信号进行盲源分离，得到源信号分量S^=[s^1，s^2，…s^M]T和分离矩阵W ；

3）计算各源信号的网格维数Di，i=1，2，…，M ，利用网格维数筛选滤波源信号，根据前期大量实测信号的试验分析，包含异常信号分量源信号的网格维数大于1.5，保守起见，采用靠近网格维数为1.5的Di曲线最大的阶跃点作为筛选条件，具体操作过程：将网格维数Di进行升序排列，以排列后的Di曲线最大的阶跃点作为筛选条件。到此便可以把源信号分量S^划分为两部分，一部分为待滤波源信号S^dl，另一部分为保留源信号S^b；

4）对滤波源信号S^dl进行RLS自适应滤波，参考信号可选网格维数较低的几个源信号组合，RLS滤波原理如图1所示；

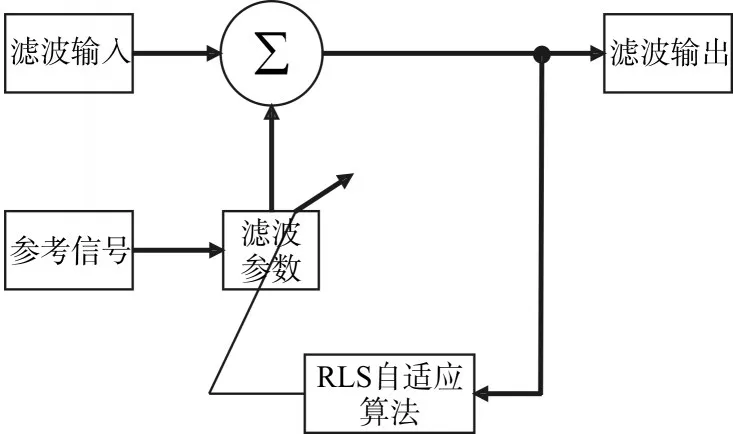
图1 RLS滤波原理图

5）将滤波后的源信号S^l与S^b进行重新组合得到重组源信号S^′，在组合的过程中保持相对位置不变，利用分离矩阵W对源信号进行重构得到X=WS^′，对相空间信号X进行还原即可得到降噪后的遥测振动信号，相空间还原方法参加文献［11～12］。

4 实验与结果分析

为验证文中提出方法的有效性，采用某次试验任务采集的遥测高频振动信号进行处理验证。采样频率为5kHz，其时域波形如图2所示。

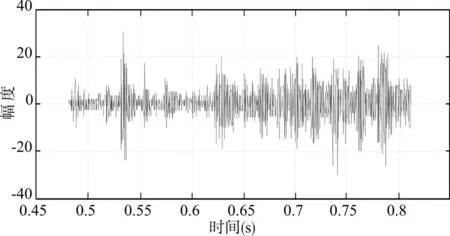
图2 采集的遥测振动信号

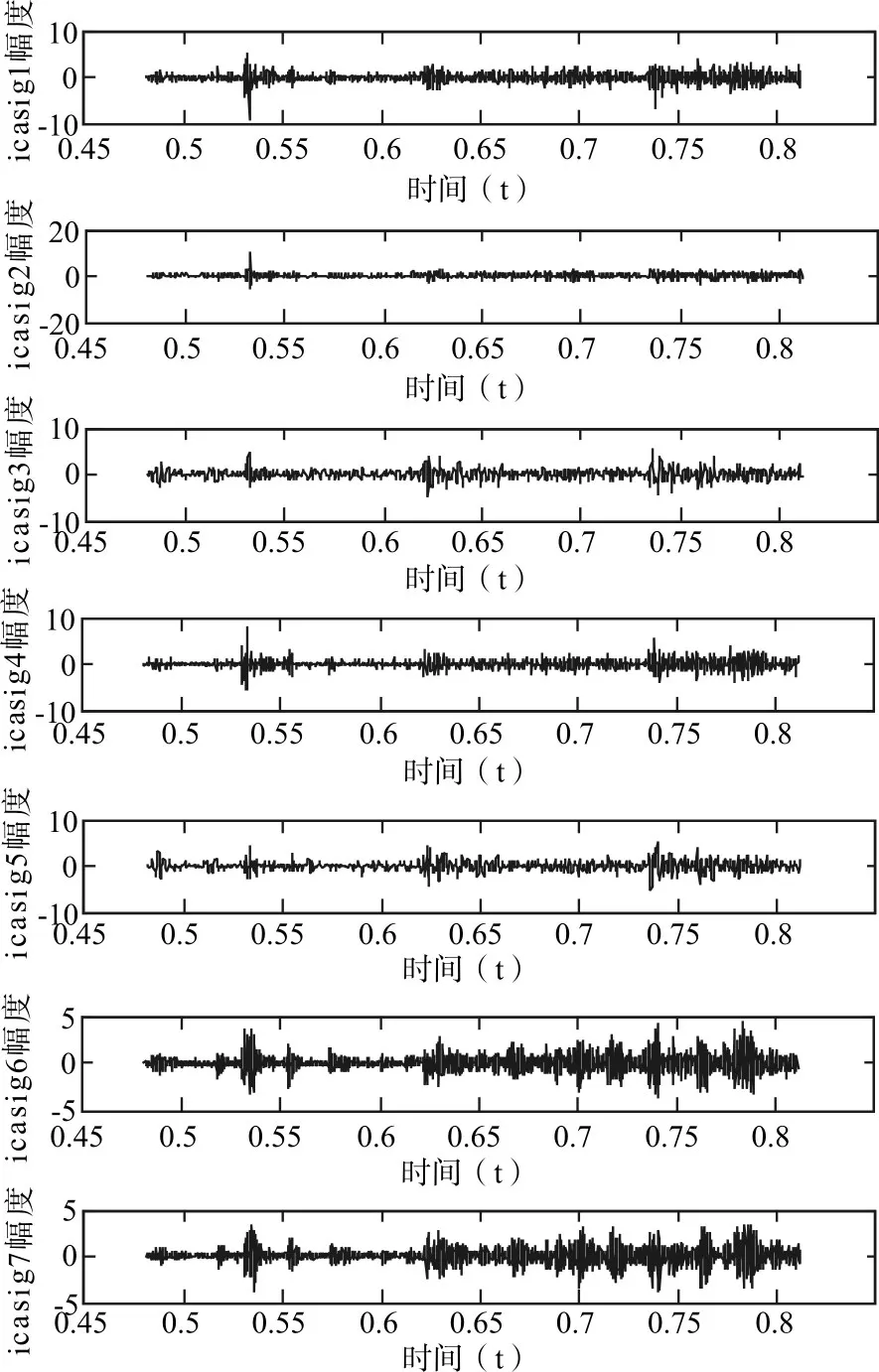
图3 ICA分离结果

利用互信息量法求取其延迟时间τ=3，Cao算法得到嵌入维数m=7，混沌相空间重构后，采用基于峭度最大化牛顿迭代ICA算法对信号进行盲源分离，得到如图3所示的7个独立源信号分量，分别求取各源信号的网格维数并进行排序，得到如图4所示的网格维数分布图，根据算法第3）步的约束条件可知，排序后源信号序号5以前的为待滤波源信号S^dl，序号为6和7的源信号为保留源信号S^b，对S^dl进行RLS滤波然后与S^b进行重组，利用第2）步估计出的分离矩阵W对源信号进行重构，相空间还原后得到滤波后的遥测振动信号，如图5所示。

从实验结果可以看出，遥测振动信号成份非常复杂，呈较大的非线性和非平稳性，本文所提的分形维数约束ICA-RLS的遥测振动信号降噪方法结合了分形分析、盲源分离与自适应滤波算法的优点，采用分形维数去约束ICA-RLS滤波过程，避免ICA-RLS将异常信号作为噪声滤除的缺点，在保证有用信息不受损失的原则下对信号进行降噪，从图4可以看出降噪后的信号更为平滑，毛刺相对减少，降噪效果较好。但降噪后信号幅度有大幅衰减，这是因为ICA算法在迭代进行盲源分离的过程中会对信号进行白化和归一化处理，幅度不确定性是ICA的固有缺陷，但幅度的变化不影响对信号频域成份的分析，不会造成时频分布的变化，对试验分析鉴定不产生影响。

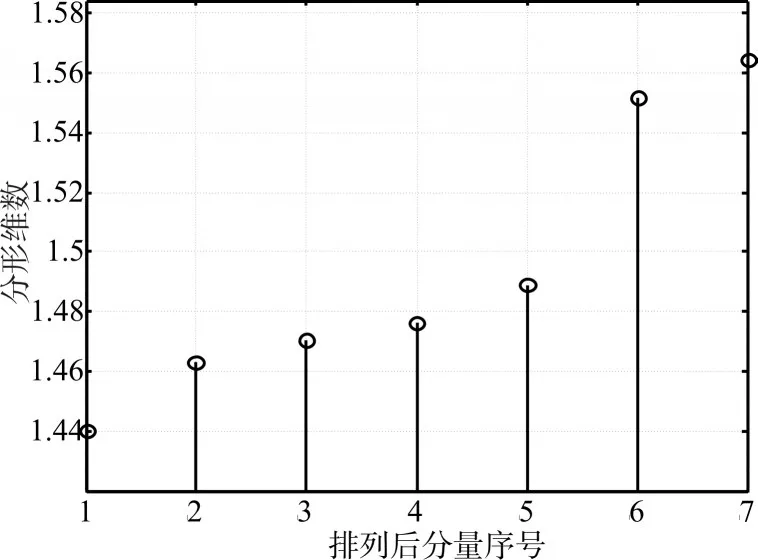
图4 网格维数分布图

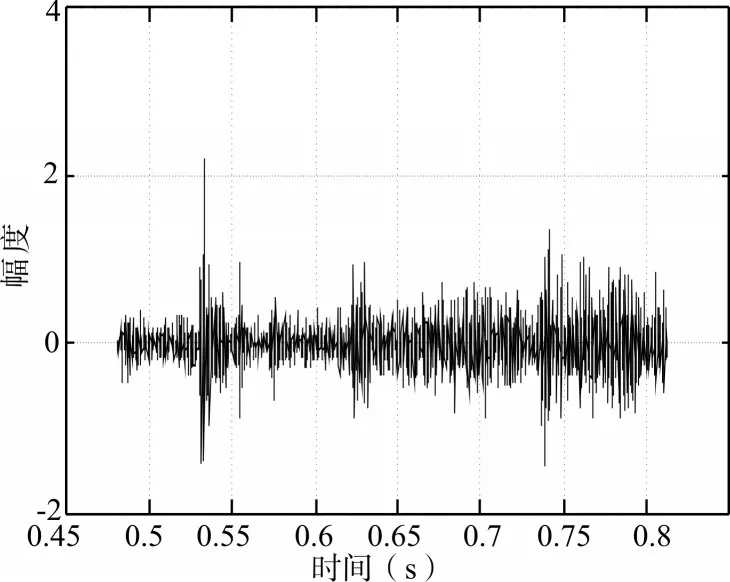
图5 滤波后的遥测振动信号

5 结语

提出一种分形维数约束ICA-RLS的遥测振动信号降噪方法，结合了分形分析、盲源分离与自适应滤波算法的优点，采用分形维数去约束ICA-RLS滤波过程，有效解决了ICA-RLS将异常信号作为噪声滤除的缺点，在保证有用信息不受损失的原则下对信号进行降噪，实测信号实验表明该方法具有较好的降噪效果，对试验的分析与鉴定有较高的理论与实用价值，同时，所提方法具有普遍的适用性，也可推广到其它降噪领域。

［1］ ZHU Dan-hua，TONG Ji-jun，CHEN Yu-quan.An ICA-based method for automatic eye blink artifact correc⁃tion in multi-channel EEG［C］//Proceeding of the 5thinter⁃national Conference on Technology and Applications in Biomedicine.Shenzhen：IEEE，2008：338-341.

［2］LI Yan-dong，MA Zhong-wei，LU Wen-kai.etal.Auto⁃matic removal of the eye blink artifact from EEG using an ICA-based template matching approach［J］.Physiologi⁃cal Measurement，2006，27（4）：425-436.

［3］HE P，WILSON G，RUSSELL C.Removal of ocular arti⁃facts from electro-encephalogram by adaptive filtering［J］.Medical Biological Engineering and Computing，2004，42（3）：407-412.

［4］Guerrero-Mosquera C，Navia-Vazquez A．Automatic re⁃moval of ocular artifacts using adaptive filtering and inde⁃pendent component analysis for electroencephalogram data［J］.IET Signal Processing，2012，6（2）：99-106.

［5］Arjunan S P，Kumar D K.Fractal properties of surface electromyogram for classification of low level hand move⁃ments from single-channel forearm muscle activity［J］.Journal of Mechanics in Medicine and Biology，2011，11（3）：581-590.

［6］Phinyomark A，Phukpattaranont P，Limsakul C.Fractal analysis features for weak and single-channel upper-limb EMGsignals［J］.Expert Systems with Applications，2012，39（12）：11156-11163.

［7］ TAKENS F.Detecting strange attractors in turbulence［M］.Dynamical Systems and Turbulence， Berlin：Springe-Verlag，1981：366-381.

［8］YANGJunyan，ZHANGYou-yun，ZHU Yong-sheng.In⁃telligent fault diagnosis of rolling element bearing based SVMs and fractal dimension［J］.Mechanical Systems and Processing，2007（21）：2012-2024.

［9］李舜酩.转子振动信号的盲源分离研究［J］.仪器仪表学报，2008，29（8）：545-549.

［10］LIShunming.Trend of the research of Blind source sepa⁃ration on vibrational signal of rotor［J］.Chinese Journal of Scientific Instrument，2008，29（8）：545-549.

［11］任丽娟，姚竹亭.分形网格维数在齿轮故障诊断中的应用［J］.机械工程与自动化，2006（6）：55-57.

［12］REN Lijuan，YAO Zhuting.The Application of Fractal in fault diagnosis of gear［J］.Mechanical Engineering&Au⁃tomation，2006（6）：55-57.

［13］Klados M A，Papadelis C，Braun C，et al.REG-ICA：a hybrid methodology combining blind source separation and regression techniques for the rejection of ocular arti⁃facts［J］.Biomedical Signal Procession and Control，2011（6）：1-10.

［14］J.Wang，Q.He，F.Kong.Adaptive multiscale noise tun⁃ing stochastic resonance for health diagnosis of rolling el⁃ement bearings［J］.IEEE Transactions on Instrumenta⁃tion and Measurement，2015，64（2）：564-577.