基于连续体模型应力评估的水下机器人刚度强化设计∗

杨 冲

1 引言

随着人工智能控制技术的发展，水下机器人的智能性越来越高，水下机器人是实现水下目标探测、目标跟踪识别和水下物体搜索等功能为一体的水下智能潜航器，水下机器人在未来的军事领域和海底作业等领域都表现出来广阔的应用价值，研究水下机器人的优化设计方法，在未来军事科学中具有重要的应用价值［1］。在水下机器人设计中，机械设计是基础，由于水下机器人处于高压强的海水中，随着作业深度的增加，对机械的抗载荷和压力要求不断提升，研究机器人的机械刚度强化设计方法是保障机器人稳定可靠工作的关键因素。

目前，对水下机器人刚度强度设计和应力评估方法采用平面约束机构模型、不规则三角网剖分模型以及尺度约束类型等［2～3］，结合对水下机器人的平行、同轴、共点、共面的运动学结构分析和连杆结构控制，在七自由度空间内进行机器人的应力评估的刚度强化设计，实现对水下机器人的机械系统动力学自动分析，提高机械强度，文献［4］中提出一种基于结构降耦和运动解耦设计的机器人刚度并联拓扑结构设计方法，采用基于Pro/E-ADAMS仿真运动曲线模型进行机器人的运动解耦性分析，根据机器人构件之间的联接关系进行应力评估和水下连杆机构的屈服效应分析，提高机器人的连杆抗压能力，但该系统结构模型对复杂结构下的机器人设计方面的应用效能不高。文献［5］中提出一种基于面三轴立铣加工控制的水下机器人的机械刚度强化设计方法，通过三轴空间结构模拟得到水下机器人连杆结构的内力分配关系，结合自由度下的应力关系进行机械加工进刀轨迹优化控制，提高了机器人的抗拉能力和应力屈服响应能力，但该机械加工方法不能对机器人的复杂曲面进行有效的应力评估，导致整个机械结构的脆弱节点较多，整体抗拉强度不好。

针对上述问题，本文提出一种基于连续体模型应力评估的水下机器人刚度强化设计方法。首先构造水下机器人刚度强化评估的应力学结构模型，进行机器人刚度强化加工的控制约束参量模型构造和分析，采用连续体模型应力评估方法进行水下机器人的钢化强度加工机械设计的荷载力学分析，实现机器人解耦构型的屈服强度等参量的准确运算，得到机器人机械结构优化构型的位置正解，进行应力评估和结构解耦性设计，最后进行了仿真测试分析，展示了本文方法在提高水下机器人机械结构性能方面的优越性。

2 机器人刚度强化评估的应力学结构模型及参数建模

2.1 约束参量分析与机器人应力学结构模型

水下机器人数学模型的刚度强化结构建立方法主要有三种，分别是七自由度屈服响应分析方法，基于拉格朗日方程的分析方法以及惯性力学分析方法，在对水下机器人机械强度和机械结构的动力学分析中，对机器人的连杆结构看作整体，进行全局受力分析，本文提出把水下机器人进行7连杆结构分解，进行动力学数学建模和力学分析［6］，首先给出水下机器人刚度强化结构设计的系统参数和变量含义描述如下：X表示水下机器人质心中心的位移；θ表示摆杆与竖直方向的角度；δ，δ.分别表示水下机器人在做航行和横滚运动角度和角速度；MP，MR分别表示机器人的主体质量和连杆部位的质量；JR=JRL=JRR，JPθ，JPδ分别表示水下机器人的横滚控制转动惯量，机器人绕通过质心且平行于Z轴的转动惯量和机器人绕运动曲线识别机构的转动惯量；R：表示机器人作业的半径；L表示并联机构原始构型的作用距离；D连杆结构之间的距离；Km，Ke表示机构自由度和末端执行点反电动势系数；UL，UR表示机械操纵自由度控制电压，以上各变量均采用国际单位。

在此基础上，给出水下机器人机械强度设计受到的几个约束条件如下

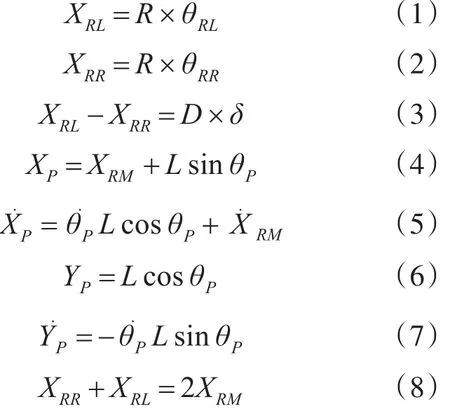
其中式（5）由式（4）微分得到，式（7）由式（6）微分得到。对水下机器人的刚度强化机械结构模型进行建模时，需要在水下应力屈服点附近进行线性化处理，选定动平台上任意一点进行机械工件运动轨迹解耦运算，在小角度的机械加工进刀范围内，取 sinθp=θp，cosθp=1，另取 JPδ是机器人的绕垂直方向轴（Y轴）的转动惯量，它的值还与θp有关，工件绕工件坐标系原点范围内不断变化，取JPθ|θP=0来代替JPδ。在对水下机器人的刚度强度主体结构设计中，采用有限元分析方法进行应力屈服响应的网格化配置，在水平荷载下分析结构试件的屈服机制和受力模型。

2.2 水下机器人机械荷载力学分析

采用连续体模型应力评估方法进行水下机器人的刚化强度加工机械设计的荷载力学分析［7］，水下机器人刚度强化构造动力学模型的数学表达式可表达为

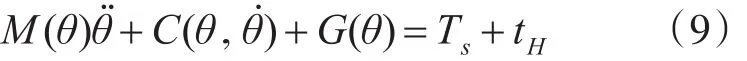
式中，θ为荷载位移，Ts为作用在水下机器人应力点上的力矩，tH为竖向荷载强度，机器人在运动时，通过最佳受力模型理论，使得tH趋于0，由此采用连续体模型预测方法，得到水下机器人的试件的屈服机制状态空间分布方程为

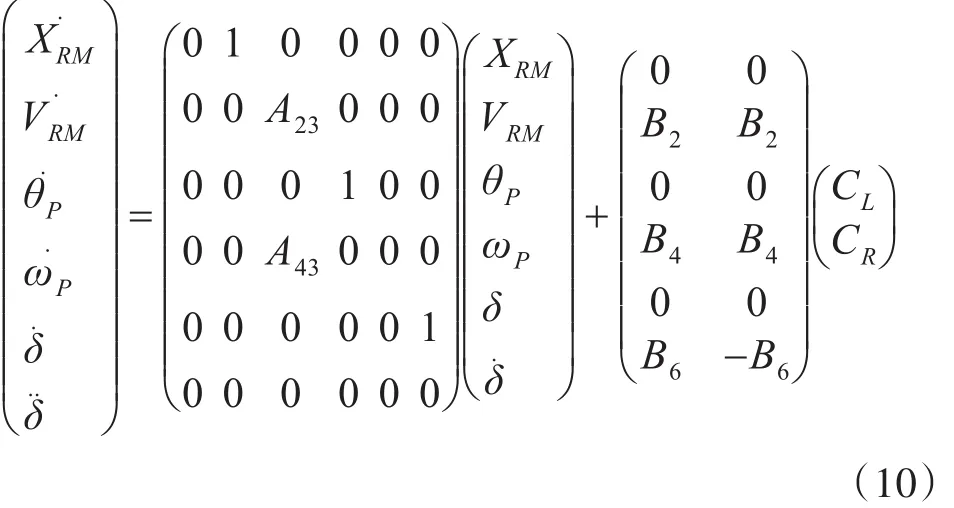
其中

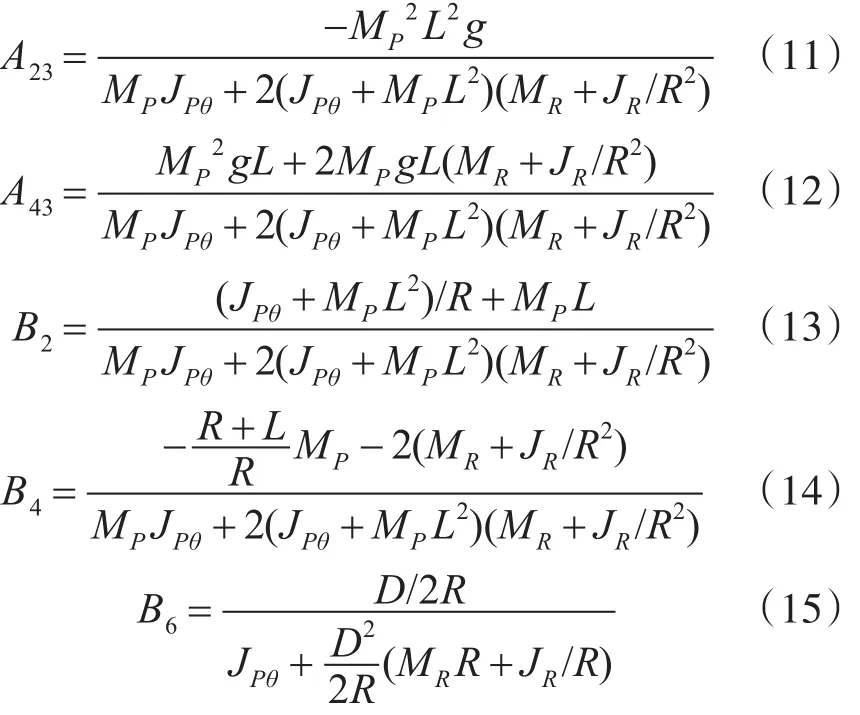
机械作用转矩C和抗拉强度U的关系为：C=Km(U-Keθ.P)，其中Km，Ke为弹性模量力矩系数和反电动势系数。可以看出水下机器人刚度强化设计中运动副轴线绕Y轴左右旋转的状态转移矩阵为常值矩阵，没有不确定性［8］，通过结构降耦合设计，能提高机械荷载。

3 水下机器人刚度强化设计优化

在上述进行了水下机器人刚度强化评估的应力学结构模型构造和刚度加工机械设计的荷载力学分析的基础上，进行水下机器人的刚度强化优化设计，本文提出一种基于连续体模型应力评估的水下机器人刚度强化设计方法。采用连续体模型应力评估方法进行水下机器人的刚度加工机械设计的荷载力学分析，实现机器人解耦构型的机构耦合度、运动灵巧度、方位特征、构件应力以及屈服强度等参量的解耦运算［9］，水下机器人的机械结构分布的连续体模型在体坐标系Oxyz中的坐标为(xa，0)，各结构耦合杆件的质心 Gi(xi，zi)，在刚度强化设计的开链回路中，水下机器人各个受力部位杆件的机构自由度分解式表达如下：

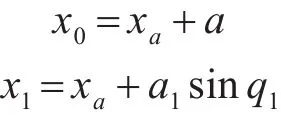
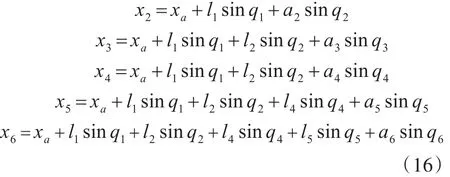
对于zi，分别为

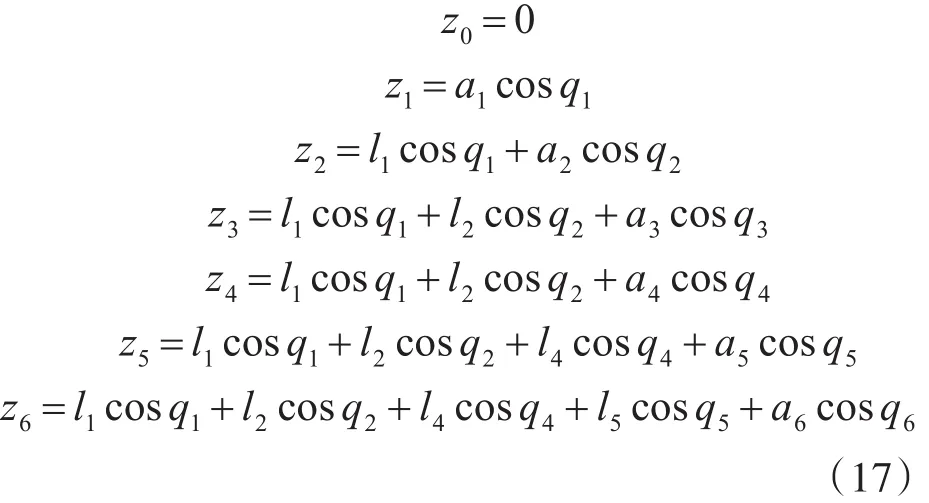
从而得到水下机器人在连续体模型中的应力评估能量估计方程为

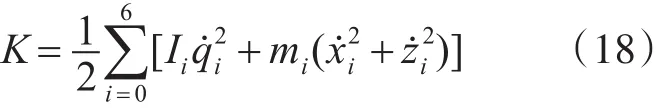
上式中，Ii为任选两条支链中的确定机构机械应力屈服响应惯量，在并联机构中水下机器人的惯性势能为

此时，水下机器人在七自由度空间中的刚度强化Lagrange函数为

机器人解耦构型的机构耦合度、运动灵巧度的关系式为

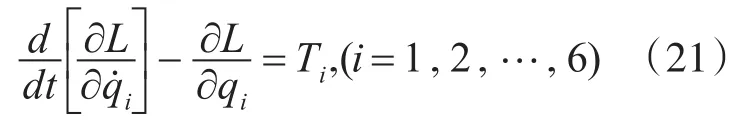
上式中，Ti为水下机器人肢体连杆的作用力矩，用M表示水下机器人质量矩阵，用向量G表示重力矢量，得到水下机器人刚度强化构件应力以及屈服强度的关系式为

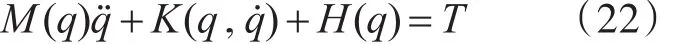
对水下机器人机械部件的运动灵巧度、方位特征、构件应力以及屈服强度等参量的解耦运算［10］，得到机器人机械结构优化构型的位置正解方程为

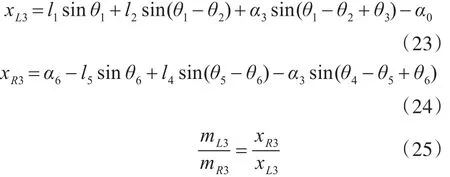
综合上四个公式，可以计算出mL3和mR3的值。通过应力评估和结构解耦性设计［11］，得到水下抗载荷和强度的计算式：

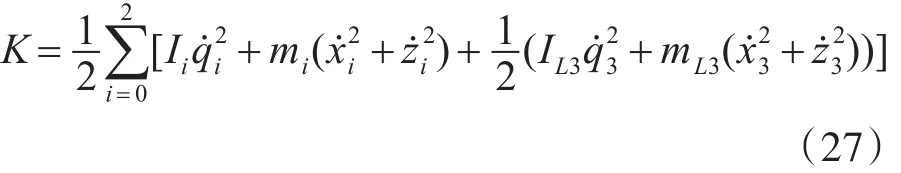
其中，Ii为机器人质心转动惯量。Lagrange动力学方程为

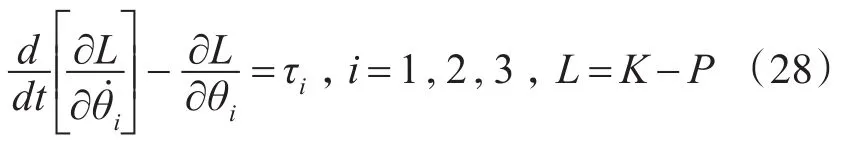
水下机器人受压屈服强度计算式为

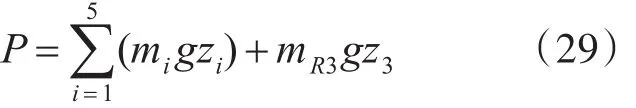
代入Lagrange动力学方程式，可以求出机械荷载作用力矩，通过应力评估和结构解耦性设计，提高水下机器人的水下抗载荷能力和强度。

4 仿真实验与性能分析

为了测试本文方法在实现水下机器人刚度强化设计，提高机器人机械设计性能方面的优越性，进行仿真实验，实验中的算法设计采用Matlab编程计算，机器人载荷和刚度应力分析采用ABAQUS有限元软件分析，机器人样机采用Smart UUV II型水下机器人作为测试对象，机器人的体结构设计中的材质选用ϕ6@200型合金材料，截面几何尺寸设定为H200mm×120mm×25mm×20mm，机器人的应力载荷测量采用三轴电子罗盘LSM303DLH，相应的建模误差、扰动误差以及测量误差矩阵的参数取值，根据上述仿真参数设定，采用不同材质进行水下机器人的表面材料设计，得到应力分布载荷如图1所示。

根据图1所示的不同材料下的机器人应力载荷分布图，使用ADAMS软件得到简化的水下机器人应力评估模型，得到水下机器人刚度强化构造动力学分析计算机视觉仿真系统，界面如图2所示。

根据上述仿真环境和参数设定，进行水下机器人刚度强化设计仿真，进行水下机器人的刚度强化分析仿真，得到，弹性荷载力学分析结果见表1，机器人的刚度强化参数计算值与试验值对比结果见表2。

分析表1和表2结果得知，水下机器人的构件承载力增大采用本文方法进行强度优化设计后，得到有效提高，刚度参数的实验值和拟合值具有很好的匹配性能，说明采用本文方法进行水下机器人刚度强化设计，能提高机器人的承载性能和应力性能。最后，为了对比性能，采用不同方法进行水下机器人机械设计，得到水下机器人的机械弹性载荷对比结果如图3所示。分析得知，本文方法进行水下机器人刚度强化设计，机器人的机械弹性载荷较高，水下应力载荷和抗压能力得到提升，性能优越。

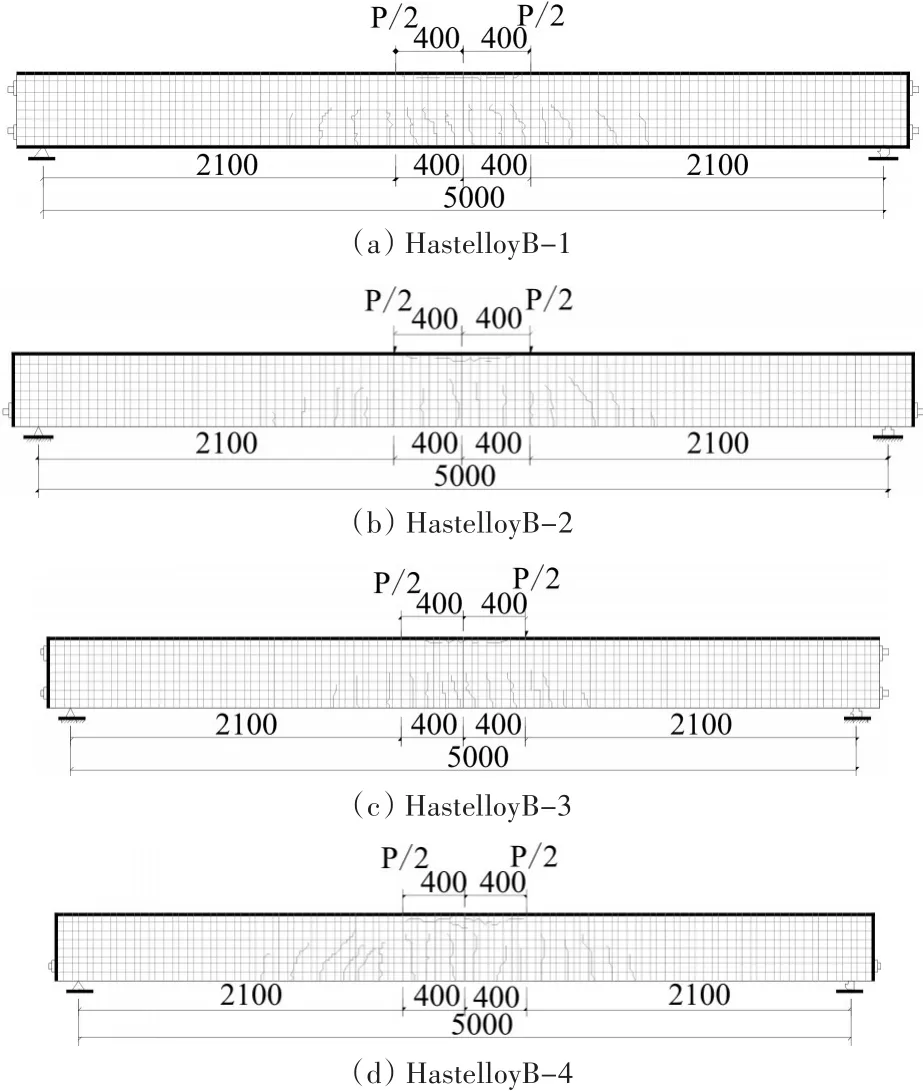
图1 水下机器人应力载荷分布

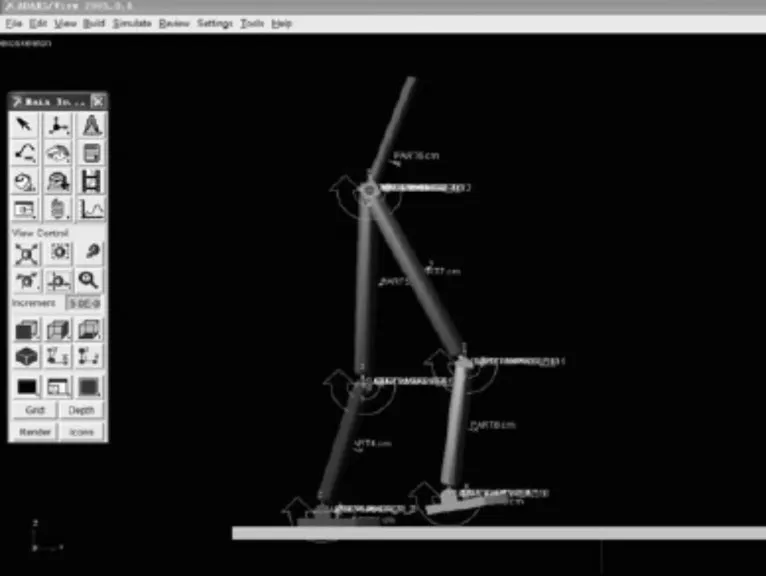
图2 水下机器人刚度强化设计的仿真界面

5 结语

为了提高水下机器人机械设计的工艺，本文提出一种基于连续体模型应力评估的水下机器人刚度强化设计方法。构造水下机器人刚度强化评估的应力学结构模型，分析机器人刚度强化加工的控制约束参量，采用连续体模型应力评估方法进行水下机器人的刚度加工机械设计的荷载力学分析，实现机器人解耦构型的机构耦合度、运动灵巧度参量的解耦运算，进行机器人机械结构优化构型的位置正解分析，通过应力评估和结构解耦性设计，提高水下机器人的水下抗载荷能力和强度。研究得知，采用本文方法进行水下机器人刚度强化设计，机器人的机械弹性载荷较高，水下应力载荷和抗压能力得到提升，在机器人机械设计的构型优选和加工工艺改进等方面具有广阔的应用前景。

表1 弹性荷载力学分析结果

表2 刚度参数与试验值对比

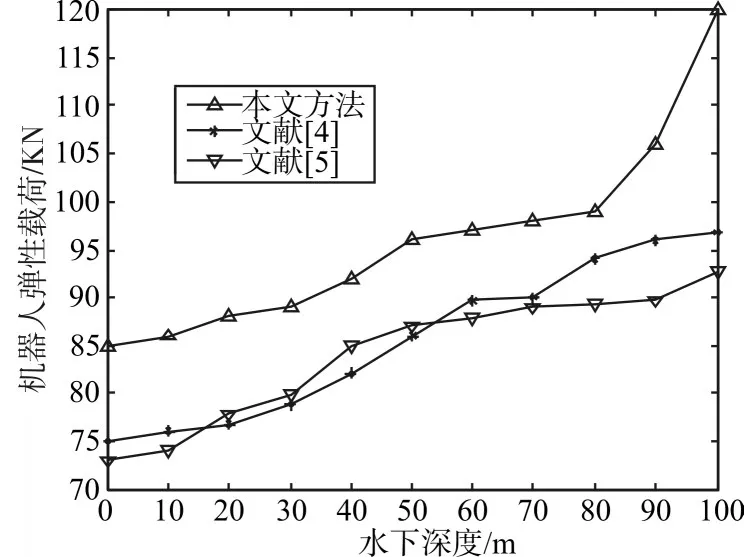
图3 水下机器人的机械弹性载荷对比结果

［1］王永强，尹韶辉，李叶鹏，等.磁流变平整加工中平动对平整度的影响［J］. 机械工程学报，2017，53（1）：206-212.

［2］李煜琦，邵珠峰，田斯慧，唐晓强.基于吊丝配重的空间机械臂零重力模拟装置卸载率分析及评价［J］.机器人，2016，38（3）：293-300.

［3］刘建娟.水下航行器组合导航蔽障控制器的设计与实现［J］.舰船科学技术，2017，39（2A）：64-66.

［4］沈惠平，李菊，王振，等.基于结构降耦和运动解耦的并联机构拓扑结构优化及其性能改善［J］.机械工程学报，2017，53（19）：176-186.

［5］Ihsan A Kareem，Mehdi GDuaimi.Improved accuracy for decision tree algorithm based on unsupervised discretiza⁃tion［J］.Int J of Computer Science and Mobile Comput⁃ing，2014，3（6）：176-183.

［6］李可，米捷.基于变结构PID的仿生机器人机电控制算法［J］.河南工程学院学报（自然科学版），2016，28（2）：32-37.

［7］刘炜，陆兴华.飞行失衡条件下的无人机惯导鲁棒性控制研究［J］. 计算机与数字工程，2016，44（12）：2380-2385.

［8］陆兴华，陈锐俊，池坤丹.引入人体红外释热探测的救援机器人感知系统［J］. 舰船电子工程，2016，36（3）：151-155.

［9］任朝晖谢吉祥周世华闻邦椿.斜齿轮-转子-轴承弯扭轴耦合振动特性分析［J］.机械工程学报，2015，51（15）：75-89.

［10］张霖，欧林林，俞立.执行能力有限的两差动轮机器人目标跟踪控制器［J］. 信息与控制，2015，44（2）：152-158.

［11］闫清东，穆洪斌，魏巍，等.双循环圆液力缓速器叶形参数优化设计［J］.兵工学报，2015，36（3）：385-390.