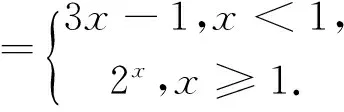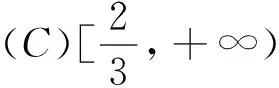内设 外求 图相助
——一类复合函数零点的判断
2018-03-23陈和平
陈和平
安徽省安庆市第二中学 (246000)
近几年比较流行一类高考数学试题,形如y=f[g(x)]的复合函数零点问题的判断,由于其计算量小、数学思想方法丰富、很深的思维层次.因此具有较好的选拔功能,试题通常作为高考小题的压轴题,受到命题者的青睐,题型有求方程解的个数及求参数取值范围.本文从解决此类问题过程、包含的思想、解题策略中提炼出几个关键词“内设 外求 图相助”与大家共享.
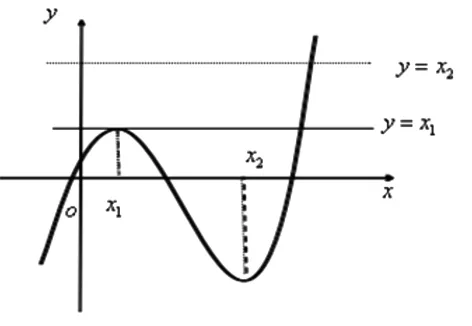
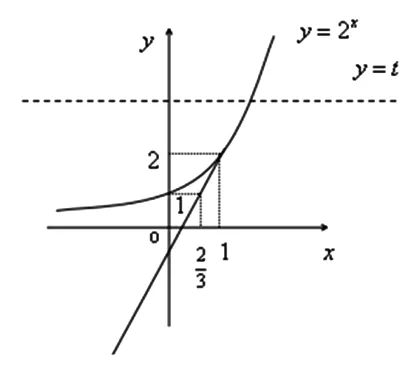
题型1 (2013年安徽理科高考)若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1 (A)3 (B)4 (C)5 (D)6 研究该题必须弄清几个关键点.首先,理解复合函数的概念,设函数y=f(x),x∈A,y=g(x),x∈B且g(x)∈A则称函数y=f[g(x)],x∈B为复合函数,通常y=f(x)称为外函数,y=g(x)称为内函数.其次,理解函数的零点(方程的解、两个函数图像的交点)的概念. 图1 解题分析:设f(x)=t,则g(t)=3t2+2at+b.由题意知:f′(x)=3x2+2ax+b导函数的零点为x1,x2(t=x1,x2)也就是y=f(x)的两个极值点.所以方程f(x)=x1及f(x)=x2解的个数(情况)进行分析,借助y=f(x)的图像与直线y=x1,y=x2的交点个数.不难看出,该题的选项为A. 特别强调的是,由于通过换元,关于方程3t2+2at+b=0的解有两个x1,x2(x1 解题时将复杂的问题化归为简单的问题,不熟悉的问题化归为熟悉的问题.运用数形结合的思想认清问题的本质,采取各个击破,找到思维的突破口. 图2 解题分析:设f(a)=t,则f(t)=2t.由分段函数得出f(t)=2t约束t的取值范围,得出满足方程f(a)=t有解时a的取值范围. 反思:2018届毕业班的复习迎考工作正在展开,课堂教学工作应扎实有效,就需要毕业班的老师探究不同的教学模式和更新教学理念.重讲题型不注重思想方法的渗透,学生的思维能力就得不到提高和升华.追求课堂容量而不花时间引导学生分析问题的本质,学生的解题能力得不到锻炼,因此复习课的课堂需要引导学生学会“数学的思维”,从而自觉地运用数学思想方法分析、解决问题,提高思维的深度和广度.真正做到“解一题、通一类、会一片”的高效复习.