信息技术视角下的幂函数探究性学习*
2018-03-23张天群
张天群
华东师范大学数学系 (200241) 牛伟强河南省洛阳市43中学 (471012)
一、引言
随着时代的发展,信息技术融入数学教学已经成为不可逆转的趋势.教师和学生恰当地使用信息技术可以完成许多传统课堂中完全做不到的事情,更有利于学生理解和掌握数学的本质,能更有效地培养学生的想象力和创造力[1].信息技术特别是其强大的可视化功能使得数学的教和学大为改观,不少研究发现信息技术可以改善学生的数学学习方式,提高学生的数学学习兴趣,促进学生数学学习成绩的提高[2-3].高中数学课程标准明确指出“数学探究课题的选择是完成探究学习的关键”.高中数学探究性学习的一个重要方法就是试验、观察、归纳、猜想和证明,简单的说就是先猜后证[4].因此,借助信息技术通过先猜后证的方法开发合适的探究性学习案例是促进高中数学探究性学习发展的重要途径.
二、教学设计
新课标人教版教材只研究几个具体的幂函数,给人一种只见树木不见森林的感觉,不利于学生数学素养的发展.鉴于此,研究者应用MATLAB软件绘制特殊的幂函数的图像,通过对幂函数图像的观察,利用先猜后证的方法引导学生分组合作探究一般情况下幂函数的性质,从而实现探究性学习的目的.
(一)新课引入
(二)探究教学
通过对α赋值研究幂函数的特例进而推测一般情况下幂函数的性质.探究从正整数开始.令α=1,2,3,4,5,6,为了便于探究,根据α的奇偶性分别画图.

图1
1.指数为正整数
当α=1,3,5时,幂函数的图像如图1(左)所示.观察可知,此时幂函数是定义域为R的增函数,并且关于原点成中心对称图形.据此,可以提出如下猜想:
猜想1:α=2k+1,k∈N时,幂函数y=xα为R上的增函数且值域为R,并且是奇函数.
师:如何证明这个猜想呢?
生:可以发现对任意x∈R,幂函数都有定义,因此它的定义域是全体实数.
师:很好,这就证明了它的定义域是全体实数,但是如何证明它是一个增函数并且是一个奇函数呢?
生:可以根据增函数和奇函数的定义来证明,课本上就是根据定义来证明的.
师:非常好!大家根据定义动手试一试,看谁先证出来.(两分钟之后)有没有同学证出来了,给大家展示一下?
生:我证出来了!当指数是正奇数的时候,幂函数的定义域为全体实数,关于原点对称,并且y(-x)=(-x)2k+1=-x2k+1=-y(x),所以y(x)为奇函数.
师:非常好!这个证明是严格的,完全正确.这样就解决了奇偶性问题.那么有没有人证明出它是增函数?
生:我证出α=1,3时它是增函数,但对于一般的正奇数不知道如何证明.
师:那就先说一下α=1,3时你是如何证明的吧!

师:非常好!事实上,这个方法对于一般的正奇数仍然是可行的.
设∀x1,x2∈R且x1 当x1,x2同为正数或负数时,因为x2k-i1xi2均为正数,所以此时y(x1)-y(x2)<0;当x1,x2一正一负时,因为x1 综上可知,α=2k+1,k∈N时,幂函数y=x2k+1为R上的增函数. 这里证明的关键是用了一个公式: x2k+11-x2k+12=(x1-x2)(x2k1+…+x2k-i1xi2+…+x2k2). 生:原来对任意正奇数它都是成立的,1和3只不过是两个最简单的情况! 师:是的. 生:我明白了. 师:那么如何证明幂函数y=x2k+1的值域是R呢? 生:当x趋近+∞时,y单调递增并趋近+∞;当x趋近-∞时,y单调递减并趋近-∞.所以α=2k+1,k∈N时,幂函数y=x2k+1的值域为全体实数. 师:很好,这样就证明了上述猜想是正确的. 到此,α为正奇数时,幂函数的定义域、奇偶性、单调性和值域我们就掌握了.如果α为正偶数时,幂函数又有哪些性质呢?我们接着往下探究. 当α=2,4,6时,幂函数的图像见图1(右).此时幂函数在(-∞,0)单调递减,(0,+∞)单调递增且始终有y≥0,并且关于y轴对称.据此,可以提出如下猜想: 猜想2α=2k+2,k∈N时,幂函数y=xα在(-∞,0)单调递减,在(0,+∞)单调递增且值域为[0,+∞),并且是偶函数. 由于篇幅所限,猜想2以及下面的猜想3-6的证明不再给出. 2.指数为正有理数 (1)p为偶数q为奇数 图2 观察图2可以发现,此时幂函数在[0,+∞)上单调递增且始终有y≥0,图形不具有对称性.据此,可以提出如下猜想: (2)p为奇数q为偶数 观察图3可以发现,此时幂函数在(-∞,0)单调递减,在(0,+∞)单调递增且始终有y≥0,并且关于y轴对称.据此,可以提出如下猜想: 图3 (3)p为奇数q为奇数 图4 观察图4可以发现,此时幂函数在R上单调递增,并且关于原点成中心对称图形.据此,可以提出如下猜想: 3.指数为正无理数 图5 观察图5可以发现,此时幂函数在定义域(0,+∞)内单调递增且始终有y>0,不具有对称性.据此,可以提出如下猜想: 猜想6 当α为正无理数时,幂函数y=xα定义域为(0,+∞),在定义域内单调递增且值域为(0,+∞),并且是非奇非偶函数. 至此,α∈R+时,幂函数的定义域、奇偶性、单调性和值域我们就理解并掌握了.如果α为0和负数时,幂函数的性质又将如何呢?限于篇幅,此处省略. 尽管探究性学习有利于培养学生的探究意识和创新能力,然而高中数学课堂教学中探究性学习并不如人意[5].高中数学探究性学习面临的一大困难就是缺乏紧扣教学内容的探究性学习案例.研究者应用MATLAB软件绘制幂函数的图像,通过对幂函数图像的观察,利用先猜后证的方法引导学生分组合作探究幂函数的性质,从而实现幂函数性质的“再发现”和“再创造”.需要指出的是这些猜想既没有必要也没有可能要求学生在一节课内完全解决,教师只需要引导学生完整地探索两三个猜想及 其证明即可,至于其他的猜想完全可以留到课下,供有兴趣的学生独自或小组合作进行探究.通过先猜后证的方式对幂函数性质的探究不仅能够帮助学生加深对幂函数性质的理解,而且有助于提高学生的数学问题提出能力和数学问题解决能力.探究过程中研究者不仅希望引导学生得到幂函数的性质,而且希望使学生初步体会到数学研究是如何进行的,体验到探究的乐趣,从而提高学生的数学学习兴趣和数学学习自信心. [1]章建跃.数学·信息技术·数学教学[J].课程.教材.教法,2012,12:62-66. [2]张春莉.试论信息技术对数学课堂教学的影响[J].课程.教材.教法,2010,1:75-79. [3]郭衎,曹一鸣,王立东.教师信息技术使用对学生数学学业成绩的影响——基于三个学区初中教师的跟踪研究[J].教育研究,2015,1:128-135. [4]牛伟强.高中数学探究性学习课题与策略研究[D].新乡:河南师范大学,2011. [5]牛伟强,熊斌.高中数学课堂中探究性学习的困惑与思考[J].教学与管理(中学版),2016,10:55-57.
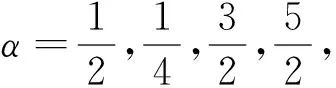








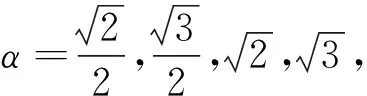

(三)结论生成(略).
三、结语
