模糊环境下低碳闭环供应链网络设计多目标规划模型与算法

李 进，朱道立

(1.浙江工商大学 管理工程与电子商务学院，浙江 杭州 310018；2.浙江工商大学 现代商贸研究中心，浙江 杭州 310018； 3.上海交通大学 安泰经济与管理学院，上海 200052)

0 引言

随着快速发展的城市化和工业化，环境污染、气候变化和全球变暖已经成为全球关注的焦点问题。2009年，我国政府明确了减少碳排放的国家目标，即与2005年相比，2020年每单位GDP的温室气体排放量减少40%～50%。美国、欧盟等国家也纷纷出台各种碳税、碳交易和碳限额政策积极控制二氧化碳的排放。在此背景下，以节能、环保和可持续发展为理念的低碳经济得到世界各国的普遍重视。供应链中的各个环节都存在能源消耗和二氧化碳排放，而供应链中的生产、运输和回收等环节更是二氧化碳的排放大户。能源、资源和环境约束的日益紧张以及中国政府对单位GDP碳排放的承诺等，加速了供应链管理向绿色低碳运营模式的转变。

消费者和政府日益关注企业的环保表现，对企业的环境责任和社会责任提出了更高的要求，越来越多消费者开始考虑所购买商品的环境记录[1]。供应链管理中的碳排放控制方法主要包括基于物理过程的碳排放控制方法和基于运作优化的碳排放控制方法两类[2]：基于物理过程的碳排放控制方法通过采用能源利用效率更高的设备、绿色产品设计和使用新能源等减少碳排放；基于运作优化的碳排放控制方法从供应链网络结构优化设计的角度减少碳排放，是一种日渐受到重视且更为有效和低成本的碳减排方法[3]，例如英国的乐购、美国的沃尔玛等均开始采用合理布局设施选址、优化货运方式和运输路线等供应链网络设计方法实践企业的碳足迹管理，并取得初步成效。供应链网络设计是一种重要的战略决策，一般需要安排供应链中设施的最佳位置、数量、容量和设施间的物流量[4]。近年来，供应链网络设计问题得到了广泛研究。学者们主要从网络的物流流向上将供应链网络设计问题划分为正向网络设计[5-6]、逆向网络设计[7-8]和闭环网络设计[4,9-10]3个类别进行研究。

供应链的全球化发展极大地增加了供应链网络中节点的数量和节点间的运输，从而增加了温室气体尤其是二氧化碳的排放量，低碳闭环供应链和绿色供应链网络设计是应对当前严峻的环境问题的有效措施。传统的闭环供应链设计问题仅考虑满足顾客需求情况下最小化成本这一经济目标，低碳闭环供应链则考虑碳排放的影响，加入了对环境目标的考量，并实现了经济目标和环境目标的平衡。近年来，学术界开始广泛关注低碳和环保供应链网络设计问题。文献[11]研究了环境投资决策对供应链网络设计问题的影响，建立了考虑总成本和环境影响的多目标优化模型;文献[12]针对有容量限制和灵活存储分配的绿色物流设施定位问题，提出一种同时考虑经济成本和二氧化碳排放的基于自适应调整拉格朗日松弛模型的演化多目标优化方法;文献[13]综合考虑供应链中从采购、制造、运输到库存管理的所有环节，建立了需求不确定下的供应链网络设计模型，探讨了碳限额与碳税等各种碳规制政策下的供应链响应决策，分析了各种政策对成本和最优网络配置的影响;文献[14]提出一种多式联运网络设计模型，该模型实现了直接采用货车运输与采用多式联运之间的站点定位和配置优化，从成本、碳排放和模式转换的视角研究了内陆网络多式联运求解的动态性;文献[15]研究了考虑能耗和碳排放的具有固定车辆数的多车型低碳路径问题，设计了基于划分的多起点禁忌搜索算法;文献[16]建立了家电闭环供应链网络设计中考虑碳补贴的网络规划模型，分析了补贴力度对消费者中绿色消费者的比例和整个网络规划的影响。

低碳闭环供应链网络设计中的另外一个重要问题是如何控制参数的不确定性。在低碳闭环供应链网络设计中，不确定性存在于供应、生产、分销、需求估计和产品回收的各个环节。供应链的动态性和复杂性大大增加了供应链决策的不确定性，从而显著地影响整个供应链网络的绩效[17]。在供应链网络设计这种战略层忽略不确定性，对整个系统造成的损害往往难以恢复，因此设计一个可靠的供应链网络，使其在参数不确定时仍然能够稳定地运作十分必要。当前常用的处理供应链网络设计不确定性问题的数学规划方法包括随机规划[18-19]和模糊规划[20]。随机规划方法无法处理缺少精确的历史统计数据和计算复杂性高的问题[21]，模糊规划则能更好地解决实际应用中缺少参数真实值的不确定性问题，是处理供应链网络设计不确定性的有效工具。

综上所述，现有文献对供应链网络设计中模糊规划问题的研究主要集中在正向或逆向物流网络设计的模糊规划问题，虽然有些文献研究了闭环供应链网络设计的模糊规划问题，例如文献[20]提出的带有清晰和模糊目标的闭环供应链网络设计问题及其遗传算法，但其研究只考虑了目标函数的模糊性，而且优化目标为单个目标，缺少对闭环供应链网络中碳排放和模糊性的综合考虑。为此，本文将探索带有参数模糊性的低碳闭环供应链网络设计(Low-carbon Closed-loop-supply-chain Network Design with Fuzziness, LCNDF)问题，建立面向LCNDF的多目标模糊规划模型，该模型利用模糊规划方法处理参数的模糊性对低碳闭环供应链网络配置的影响；其次，模型还将综合考虑战略层的制造工厂、回收中心和处置中心的选址与数量决策，以及战术层的网络节点间多产品流和多运输方式的选择决策；另外，除了成本目标外，该模型还有一个最小化碳排放的环境目标，低碳目标将考虑设施建设、网络节点间的车辆运输、设施中产品的不同处理流程等各种排放源产生的碳排放。为了求解该模型，本文还将设计一种交互式ε约束算法(Interactive Epsilon-constraint Algorithm, IEA)。

1 模型的建立

1.1 问题描述

本文研究的供应链网络是一个集成正向和逆向物流的多层级、多产品的闭环供应链网络，如图1所示。正向网络包括制造工厂和客户两级主体，制造工厂负责新产品制造和回收产品的再制造，产成品直接从制造工厂销往客户点。逆向网络包括客户、回收中心和处置中心三级主体，其中：回收中心负责从客户处回收已消费的产品，并对回收产品进行检验和测试，根据检验结果将可再制造的产品送往制造工厂，将废弃品送往处置中心；处置中心负责废弃品的填埋、焚烧和丢弃等处理。假设：客户点位置固定且对每类产品的需求均已知，设施具有容量限制；产品通过正向物流进行分销，已消费产品采用逆向物流系统进行回收和处置；销往任一客户点的产品，消费完后该产品或其部件从同一客户点回收；从客户点到制造工厂回收再利用产品的运输成本小于该产品再制造可以节约的生产成本;各网络节点间有多种运输方式可供选择，每种运输方式的容量和碳排放不同。采用梯形模糊数对客户点的需求量、产品的单位生产成本、产品的单位运输成本和产品的单位处置成本等模糊参数进行表示。

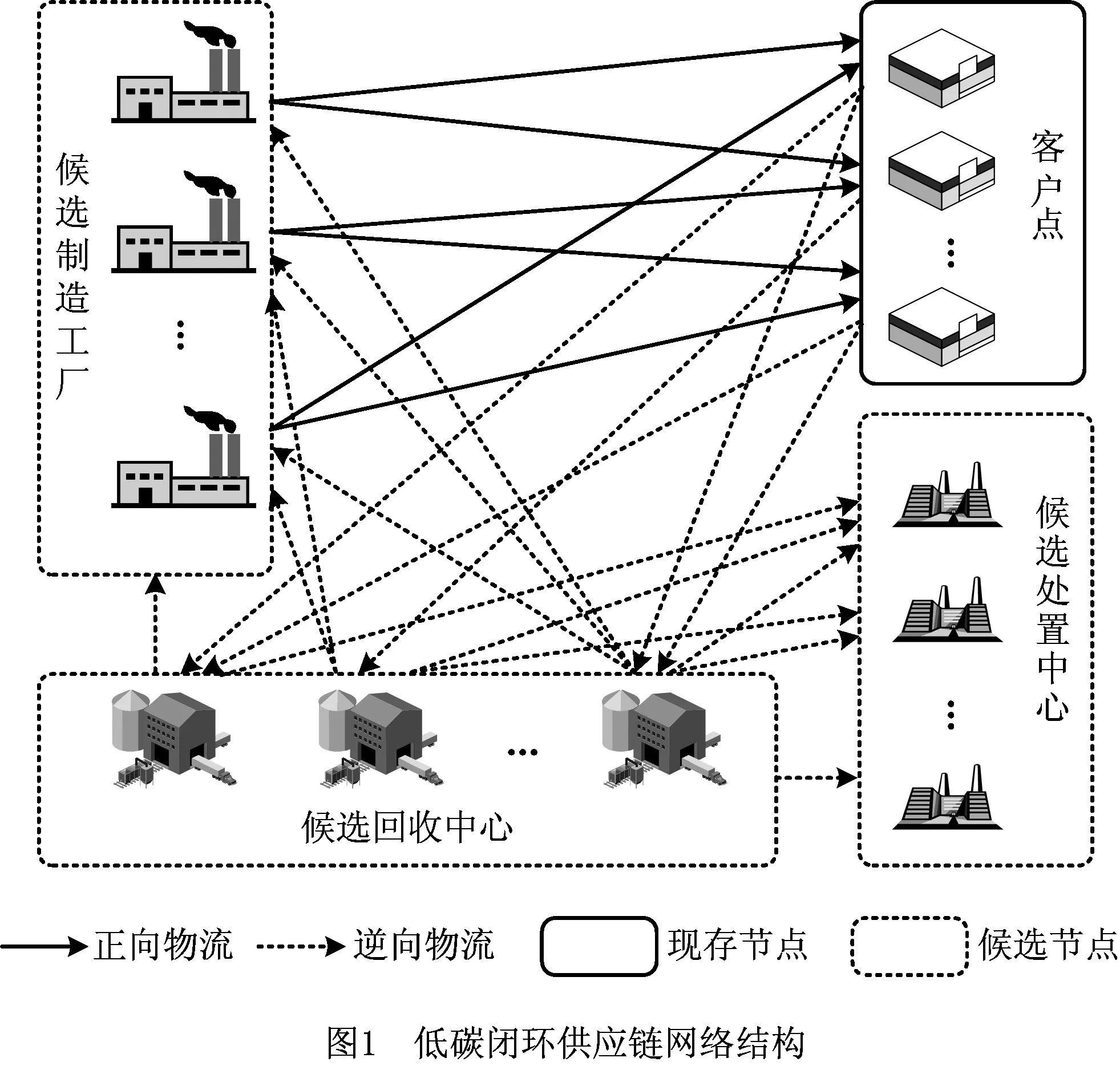
基于以上假设条件，本文需要决定：在战略层面，确定建立制造工厂、回收中心和处置中心的最佳位置和数量；在战术层面，确定闭环供应链网络节点间正向和逆向的产品流与运输方式，满足所有客户点的需求，目标是实现闭环供应链网络设计的总成本和总碳排放最小化。因为最小化总成本的经济目标和最小化总碳排放的环境目标存在冲突，所以本文将研究如何通过战略和战术两个层面的决策选择合理地平衡这两个目标；同时，本文还将利用模糊规划方法进行建模，探讨网络参数的模糊性对LCNDF的影响。

1.2 符号说明

定义如下参数和变量：

(1)参数

I为候选制造工厂节点集合,J为候选回收中心节点集合，K为客户点集合，L为候选处置中心节点集合，P为产品类型集合，T为可用运输方式集合。

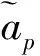
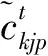
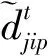
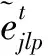
fi为制造工厂i的固定建设费用，i∈I；

gj为回收中心j的固定建设费用，j∈J；

hl为处置中心l的固定建设费用，l∈L；

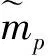
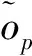
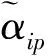
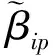
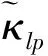
tik为制造工厂i到客户点k之间的距离，i∈I，k∈K(同样可定义tkj，tji和tjl)；

rkp为从客户点k回收的产品p的数量，k∈K，p∈P；

λp为产品p的平均处置率，p∈P；

evt为采用运输方式t每辆车每千米的二氧化碳排放量，t∈T；

eci为建设制造工厂i的二氧化碳排放量，i∈I；

emip为制造工厂i每制造/再制造一个产品p所产生的二氧化碳排放量，i∈I，p∈P；

erj为建设回收中心j的二氧化碳排放量，j∈J；

etjp为回收中心j每处理完成一个回收产品p所产生的二氧化碳排放量，j∈J，p∈P；

edl为建设处置中心l的二氧化碳排放量，l∈L；

eslp为处置中心l每处置完成一个废弃产品p所产生的二氧化碳排放量，l∈L，p∈P；

vct为运输方式t的车辆容量，t∈T。

(2)决策变量

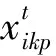
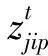
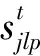
ui在候选节点i处建立制造工厂时为1，否则为0，i∈I；

vj在候选节点j处建立回收中心时为1，否则为0，j∈J；

wl在候选节点l处建立处置中心时为1，否则为0，l∈L。

1.3 模型构建

针对所研究的LCNDF含有模糊参数的问题，拟采用机会约束模糊规划方法建立研究模型。常用的模糊规划模型主要有期望值模型、机会约束规划模型和相关机会规划模型[22]，相比之下，机会约束规划模型可以使用可能性(Pos)和必要性(Nec)测度，能够使决策者控制机会约束成立的置信水平，同时也支持三角形和梯形等各种模糊数形式。必要性测度能够直接将模糊机会约束转化成相应的清晰等价形式，且在处理机会约束上更具有实际应用意义[23]。为此，本文对目标函数中的不确定参数采用期望值方法进行建模，对机会约束规划采用必要性测度进行建模，并采用梯形模糊分布处理模型中的模糊参数。

基于上述分析，本文将LCNDF描述为如下的机会约束多目标模糊规划模型M1：

(1)

(2)

s.t.

(3)

∀i,p;

(4)

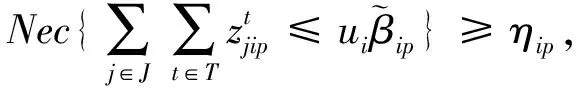
(5)

(6)

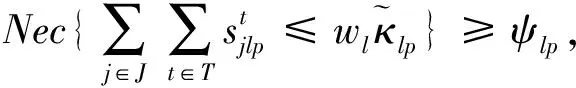
(7)

(8)

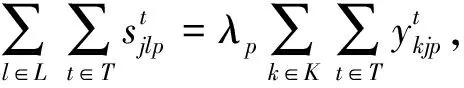
(9)

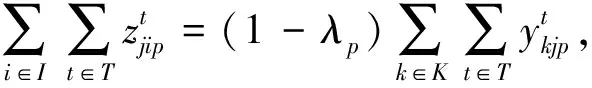
(10)

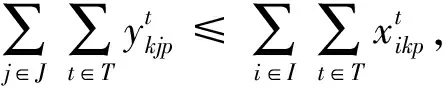
(11)

(12)

δkp,φip,ηip,θjp,ψlp∈[0.5,1],

∀i,j,k,l,p,t。

(13)

其中：目标函数(1)使总期望成本最小，包括制造工厂、回收中心和处置中心的固定建设成本,从制造工厂到客户点的产品生产期望成本和运输期望成本,从客户点到回收中心的运输期望成本,从回收中心到制造工厂的回收可节约生产期望成本和运输期望成本，从回收中心到处置中心的处置期望成本和运输期望成本；目标函数(2)是使总二氧化碳排放量最小，包括网络中各节点间运输产生的二氧化碳排放量，制造工厂、回收中心和处置中心各设施建设产生的二氧化碳排放量，以及产品在设施中进行各种处理产生的二氧化碳排放量；式(3)表示完全满足所有客户点对不同产品需求的必要性测度不小于δkp，δkp∈[0,1]；式(4)～式(7)表示制造工厂、回收中心和处置中心满足容量约束的必要性测度不小于φip，ηip，θjp和ψlp，这些约束也保证只能在建立的制造工厂、回收中心和处置中心运送产品；式(8)保证所有客户点的回收产品都能够被收集；式(9)确保每种回收产品都具有一定的平均处置率；式(10)为在回收中心处每种产品的流守恒约束；式(11)和式(12)表示在客户点和制造工厂的正向流总是不小于逆向流；式(13)为对应决策变量的非负约束和0-1约束。

本文的模糊规划模型将机会约束最低的置信水平作为一定范围内的决策变量，该变量基于模型的目标函数和约束进行优化。因此，决策者不需要决定机会约束置信水平的最优值，该模型能够主动管理参数的不确定性。同时，模型还综合考虑了战略层的候选制造工厂、回收中心和处置中心的设施选址决策，以及战术层网络节点间双向多产品流和多种运输方式的选择决策，从而保证了所建模型的新颖性和实用性。

1.4 清晰等价模型

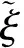
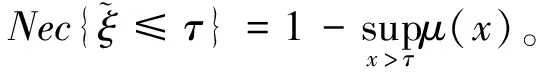
(14)

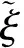
(15)

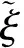
(16)

(17)

根据式(16)和式(17)，有如下定理成立：

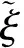
⟺τ≥(1-α)τ3+ατ4,

(18)

(19)

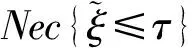
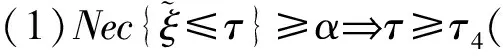
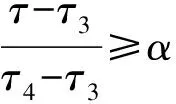
因此，式(18)成立。证毕。同理也可证明式(19)成立。

根据梯形模糊数的期望值，以及式(18)和式(19)，可将机会约束多目标模糊规划模型M1转化为如下清晰等价模型M2：

(20)

目标函数2同式(2)。

s.t.

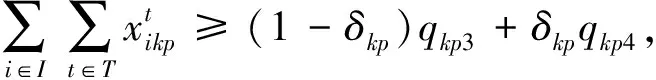
(21)

∀i,p;

(22)

∀i,p;

(23)

∀j,p;

(24)

∀l,p;

(25)

式(8)～(13)。

2 交互式ε约束算法

本文所研究的是一个多目标模糊规划模型。目前，常用的多目标问题求解方法主要有先验式、交互式和后验式方法3种[24]。相比之下，交互式方法具有高效性和灵活性的特点，可以按照决策者的偏好对每个目标函数的满意水平进行交互和渐进地测量与调整，从而确保得到的最优解能够更好地满足决策者的偏好要求。为此，本文提出一种交互式ε约束算法。

在缺少信息的情况下，多目标问题的Pareto最优解没有优劣之分，通常决策者需要提供额外的偏好信息来选择最优解。多目标优化问题一般包括优化和决策支持两个部分。本文采用ε约束方法对多目标问题进行优化求解以获得Pareto最优解，ε约束方法能够通过调整目标函数约束的ε获得不同的最优解，适合非凸问题求解，同时本文的ε约束方法还具有如下特点：①对每个目标函数通过字典序优化保证构建的支付矩阵只含有Pareto最优解；②通过引入松弛变量将目标函数约束转换为等式约束，确保了有效解的产生[25]。另外，本文采用交互式方法,有利于引导解的搜索向决策者的偏好解收敛，从而帮助决策者选择最符合其偏好的Pareto最优解，该交互式方法具有如下优点：①每次迭代，决策者可以选择多个Pareto最优解；②通过将决策者选择的解的目标函数增加上界约束来缩小搜索空间；③不用限制算法迭代的次数，决策者根据其所获得的解的满意度决定算法的终止。

交互式ε约束方法的具体步骤如下：

步骤1利用模糊参数的期望值以及式(18)和式(19)将模糊目标函数和机会约束转化为清晰等价形式。

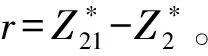
步骤4基于第2个目标函数的变化范围，设定网格点的数量为g。

步骤5将第2个目标函数作为约束，对于每个网格点，求解如下问题P：

minZ1(X)-ρs/r。

s.t.

X∈S,Z2(X)+s=ε。

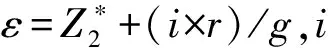
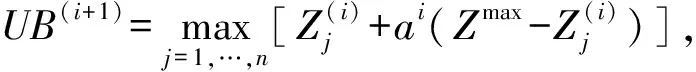
3 算例

本文采用如下算例验证模型和算法的有效性与可行性。某办公电器(生产复印机和扫描仪等)制造商负责一地区两种产品的制造/再制造和回收，计划重新设计其闭环供应链网络以更好地满足顾客需求。制造商在该地区拥有6家客户区域、4个候选制造工厂、4个候选回收中心和2个候选处置中心。结合实际企业应用数据的调研结果，本文利用均匀分布随机产生各参数值，并给出产生各参数的分布与均值，其中与经济目标相关的确定参数和模糊参数设置如表1所示，与碳排放目标相关的参数设置如表2所示。选用两种类型货车负责产品运输，第1种货车的容量为vc1=100，第2种货车的容量为vc2=160，两种类型货车的碳排放量如表2所示。

在以上算例设置下，多目标规划模型M1或M2拥有决策变量388个、约束条件88个。针对该大规模复杂性较高的问题，考虑到LINGO软件在交互式计算和求解优化规划模型方面的优势，本文利用LINGO 11.0编写算法程序进行求解，运行计算机CPU为i5-5 200 U 2.20 GHz PC(4.00 GB SDRAM)。对于交互式ε约束算法，经初步计算实验，设定g=20，n=3。

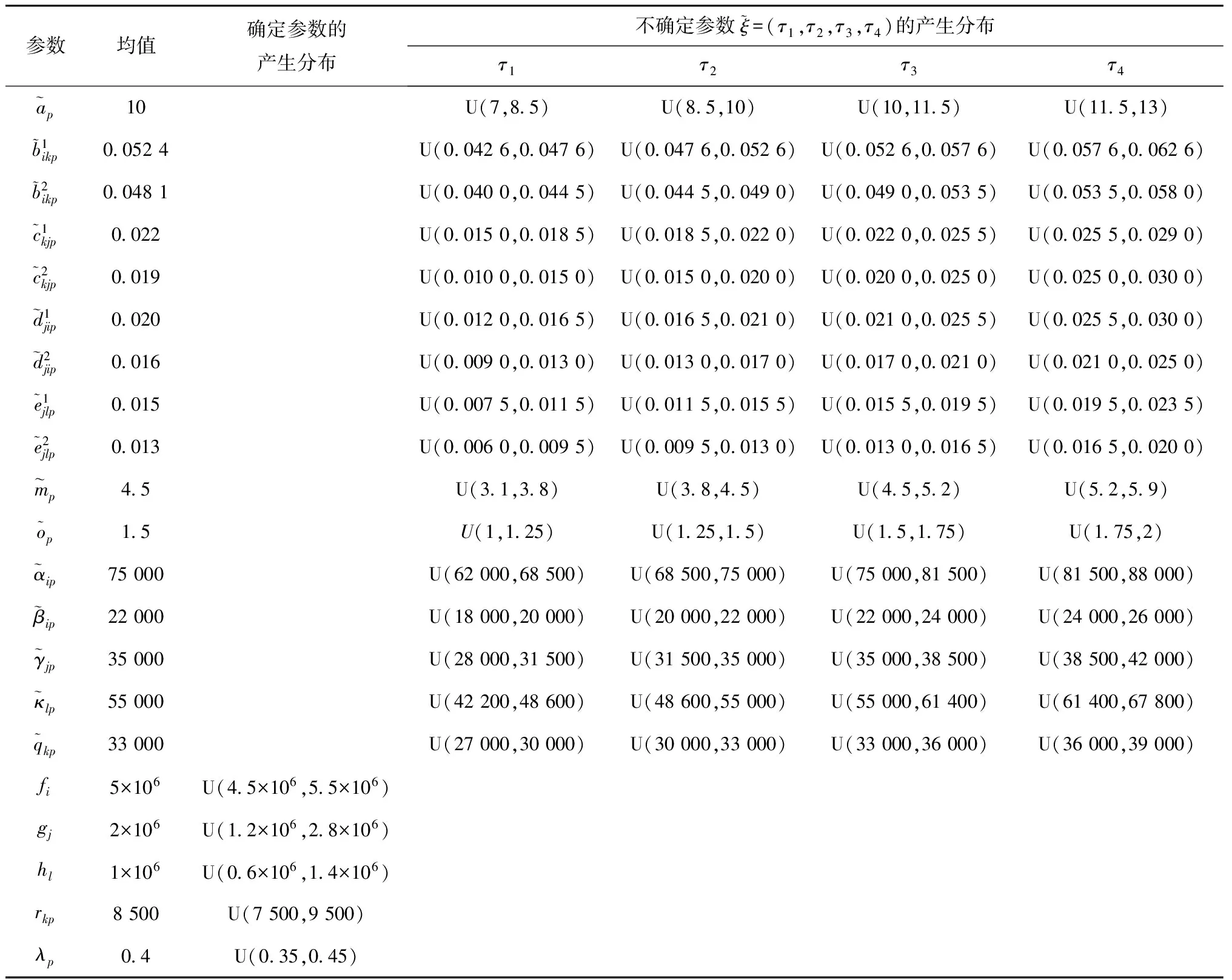
表1 与经济目标相关的参数设置

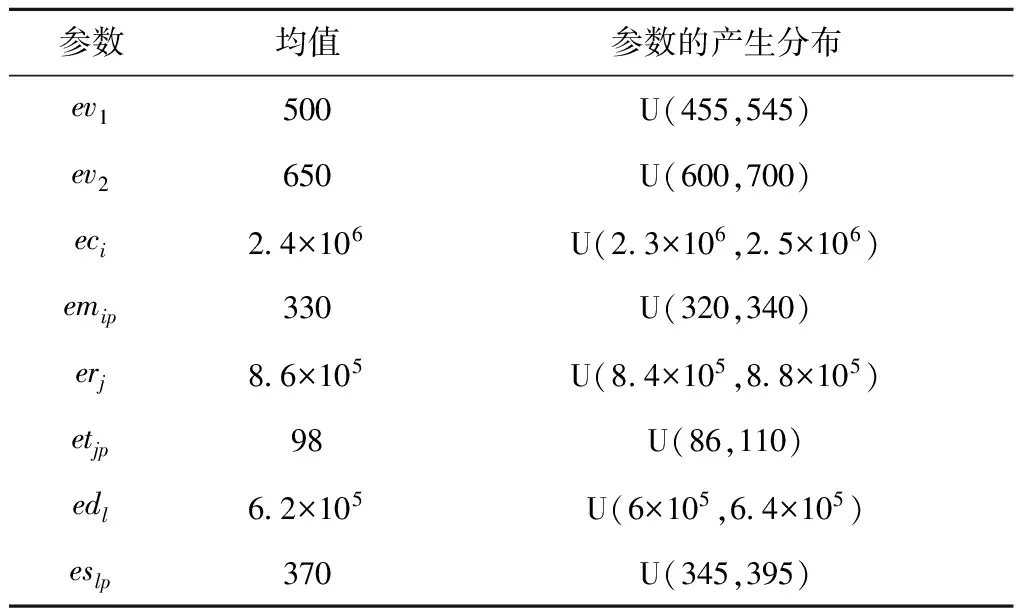
表2 与碳排放目标相关的参数设置

3.1 算法比较

为了验证算法的有效性，将本文的IEA与传统的ε约束算法[25](Conventional Epsilon-constraint Algorithm, CEA)和基于字典序优化的ε约束算法(Lexicographic Optimization-based Epsilon- constraint Algorithm, LOEA)进行比较。为了使多目标问题具有可比性，设定第1个目标函数的权重为0.6，第2个目标函数的权重为0.4，在IEA中，决策者将选择目标函数加权值最小的解，若后续10次迭代没有发现更好解，则算法终止。

按照表1的方法利用均匀分布随机产生10组测试用例，这些算法均采用LINGO 11.0编写算法程序，运行计算机为i5-5 200 U 2.20 GHz PC(4.00 GB SDRAM)。表3所示为各算法的计算结果，对比指标包括加权目标函数值(WObj)、目标函数1的值(Obj1)、目标函数2的值(Obj2)、算法的计算时间(CPU(s))、计算结果的均值(Ave.)和标准差(Std.)。

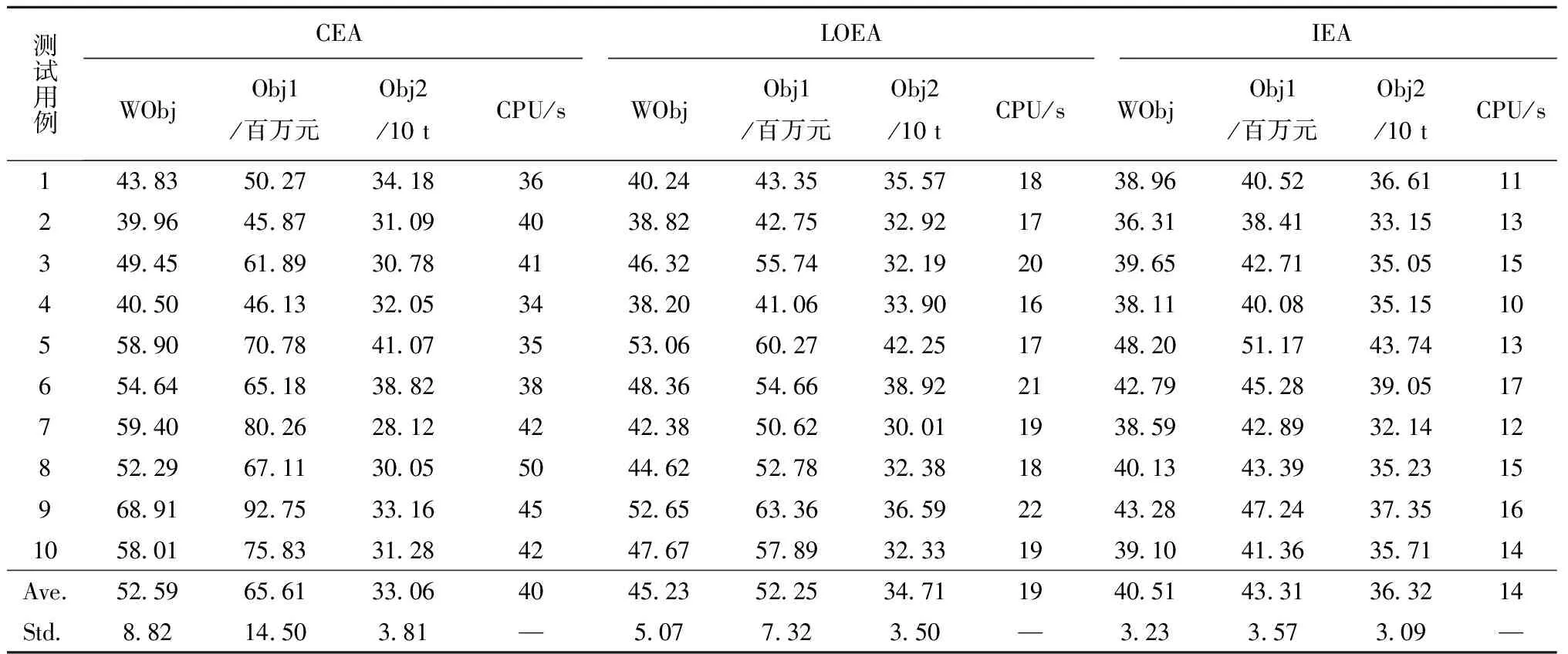
表3 算法比较的计算结果

由表3可以看出，IEA和LOEA的平均加权目标函数值比CEA分别减少了29.82%和16.27%，说明采用字典序优化有利于算法跳出局部最优解，可以提高求解质量。LOEA算法的平均计算时间比CEA算法减少了110.53%，说明字典序优化方法能够大幅节约计算时间，提高计算速度。相比之下，IEA算法的平均加权目标函数值比LOEA算法减少了11.65%，计算时间也更短，说明采用交互式方法和目标函数转换进一步提高了算法的收敛速度和求解性能。另外，IEA计算结果的标准差比LOEA和CEA更小，说明IEA具有更好的可靠性和鲁棒性。综上所述，算法对比表明，所设计的IEA是求解LCNDF问题的一种有效算法。

3.2 确定模型和模糊模型的求解结果比较

选取一组测试用例，首先研究M1为确定模型时，即仅包含确定性参数(本文采用不确定参数的均值作为确定参数的计算数据)，求解确定模型得到的结果为：目标函数1的最优值为3.41×107元，需要选择建立制造工厂1,3,4、回收中心3和4、处置中心2；目标函数2的最优值为298.16 t，需要选择建立制造工厂1,3和4、收回中心1和3、处置中心1。对于具有不确定参数的模糊规划模型，利用IEA计算得到的10次迭代结果如表4所示。从表4可以看出，与确定模型相比，模糊规划模型目标函数1的最优值增加了16.63%，目标函数2的最优值增加了14.88%，说明考虑模糊性会增加经济成本和碳排放。另外还可以看出，当闭环供应链网络中含有模糊参数时，减少碳排放在超过一定临界值(如本例中的361.15 t)时会导致经济成本急剧上升。

表4 模糊规划模型的计算结果

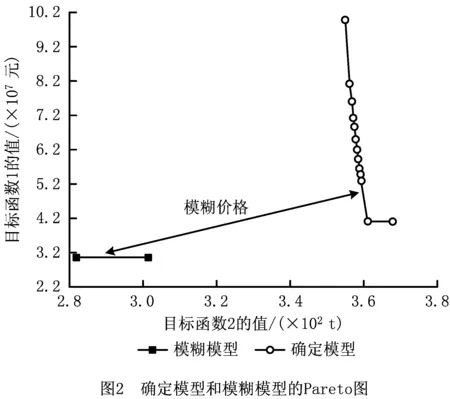
图2所示为不同算法迭代下计算得到的确定模型和模糊模型的Pareto图。由图2可以看出，模糊规划模型的Pareto图是一个下降曲线，说明减少碳排放会导致经济成本上升；由曲线的趋势进一步可以看出，当碳排放较大时，减少碳排放需要支付较低的经济成本，而当碳排放较小(小于某临界值)时，降低碳排放需要支付更大的经济成本。此外，确定模型的目标函数值总优于模糊模型，供应链网络设计的成本也更低，对于决策者来说，当模糊模型中考虑不确定参数时会增加经济成本，称为模糊价格，即为了应对模糊性需要在闭环供应链网络设计中增加配置的成本，如图2所示。

3.3 模糊规划模型的最优置信水平分析

为了说明模糊规划模型对置信水平的优化效果，拟对模糊规划模型在不同置信水平下的计算结果进行对比分析。根据表1的数据随机产生10组测试用例，分别取模糊规划模型的机会约束置信水平α=0.7,0.8,0.9，在不同测试用例下计算模糊规划模型的解，并与优化置信水平下的模糊规划模型最优解进行比较，采用加权目标函数值作为评价指标，计算结果如表5所示。

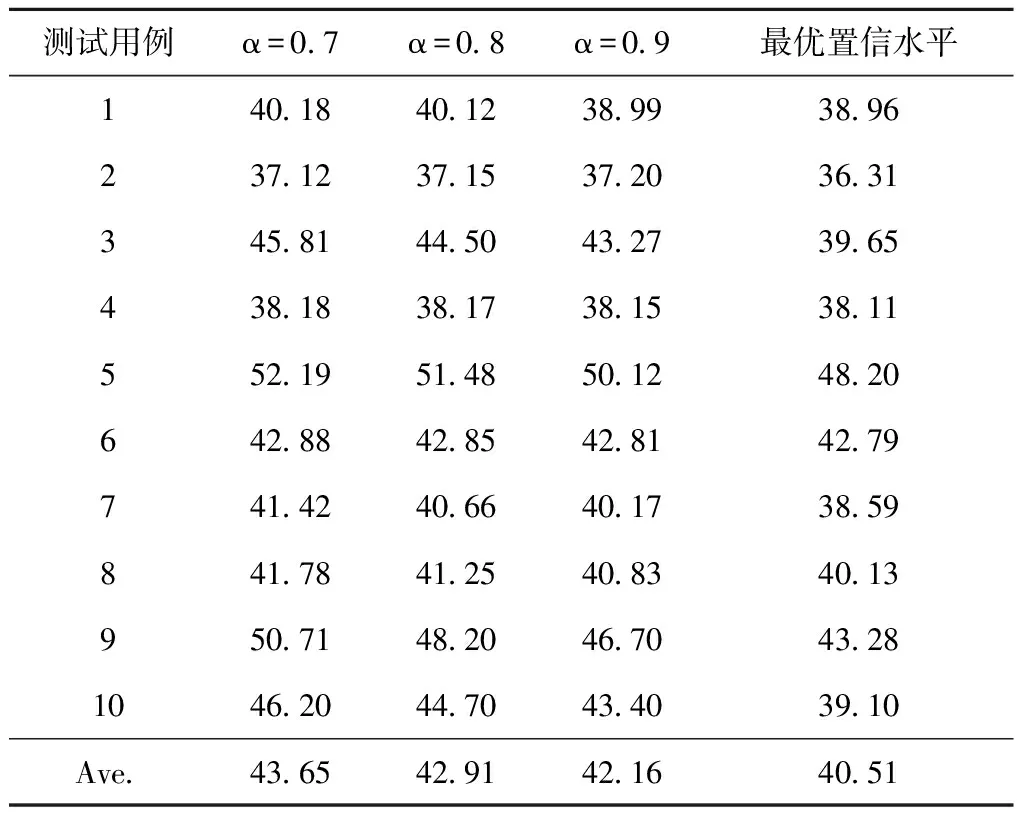
表5 不同置信水平下的求解结果对比

从表5可以看出，在10组测试用例下，优化置信水平的模糊规划模型分别比固定置信水平为α=0.7,0.8,0.9的模型产生的平均加权目标函数值减少了7.75%,5.92%和4.07%，且优化置信水平的模糊规划模型均产生了更优的解，说明模糊规划模型通过优化机会约束最低置信水平可以实现经济目标和环境目标的有效平衡。

4 结束语

供应链中的生产、运输和回收等环节存在大量的能耗和碳排放，发展低碳供应链是实现可持续发展和低碳经济的必由之路，研究低碳闭环供应链网络设计问题可以为有效和低成本地控制碳排放提供决策支持和方法指导。

针对模糊环境下集成正向和逆向物流的多层级、多产品的，涉及制造工厂、客户、回收中心和处置中心多个参与主体的闭环供应链网络设计问题，建立了LCNDF的机会约束多目标模糊规划模型。该模型不仅考虑供应链网络设计中最小化总成本和总二氧化碳排放两个目标，还综合考虑了供应链网络参数的模糊性、多产品流和多种运输方式的选择等特点，更符合闭环供应链网络设计的实际情况。同时，该模型还将机会约束的最低置信水平作为决策变量，实现了对机会约束置信水平的优化，从而可以合理地平衡经济目标和环境目标。此外，本文还设计了一种IEA对建立的模型进行求解。最后，通过一个制造商的算例验证了模型和算法的有效性和可行性。数值结果分析表明，模糊规划模型能够有效地处理低碳闭环供应链网络的参数模糊性，对于决策者来说，降低碳排放会增加经济成本，特别在大于一定临界值时，减少碳排放将支付较低的经济成本，而小于该临界值会导致经济成本急剧上升；同时，应对低碳闭环供应链网络的模糊性也会增加经济成本，即需要支付模糊价格。

进一步研究将综合考虑供应链网络的参数不确定性和多周期性、战略层的设施定位和战术层的库存与运输等决策，对现有模型进行完善，建立更加灵活的模糊规划模型，如鲁棒模糊规划模型、动态模糊规划模型等。另外，随着全球对可持续发展的日益重视，在可持续供应链网络设计中进行综合经济、环境和社会层面的研究将是未来的一个发展方向。

[1] LASH J, WELLINGTON F. Competitive advantage on a warming planet[J]. Harvard Business Review,2007,85(3):94-102.

[2] CHEN Jian. Study on supply chain management in a low-carbon era[J]. Journal of Systems & Management,2012,21(6):721-728(in Chinese).[陈 剑.低碳供应链管理研究[J].系统管理学报,2012,21(6):721-728.]

[3] BENJAAFAR S, LI Y Z, DASKIN M. Carbon footprint and the management of supply chains:insights from simple models[R]. Minneapolis，Minn.,USA:University of Minnesota,2009.

[4] PISHVAEE M S, FARAHANI R Z, DULLAERT W. A memetic algorithm for bi-objective integrated forward/reverse logistics network design[J]. Computers & Operation Research,2010,37(6):1100-1112.

[5] NI Linglin, SHI Feng. Hub location and allocation optimization of multiple allocation hub-and-spoke express networks[J]. Systems Engineering—Theory & Practice,2012,32(2):441-448(in Chinese).[倪玲霖,史 峰.多分配快递轴辐网络的枢纽选址与分配优化方法[J].系统工程理论与实践,2012,32(2):441-448.]

[6] MA Weimin, LI Bin, XU bo, et al. Reliable supply chain network design under facility disruption and demand uncertainty[J]. Systems Engineering—Theory & Practice,2015,35(8):2025-2033(in Chinese).[马卫民,李 彬,徐 博,等.考虑节点中断和需求波动的可靠供应链网络设计问题[J].系统工程理论与实践,2015,35(8):2025-2033.]

[7] FRANCAS D, MINNER S. Manufacturing network configuration in supply chains with product recovery[J]. Omega,2009,37(4):757-769.

[8] LEE D H, DONG M. Dynamic network design for reverse logistics operations under uncertainty[J]. Transportation Research Part E:Logistics and Transportation Review,2009,45(1):61-71.

[9] CHEN Y T, CHAN F T S, CHUNG S H. An integrated closed-loop supply chain model with location allocation problem and product recycling decisions[J]. International Journal of Production Research,2015,53(10):3120-3140.

[10] ZHAO Xiaomin, HUANG Peiqing. Modeling and simulation on a SM closed-loop supply chain system[J]. Journal of Management Sciences in China,2011,14(5):29-42(in Chinese).[赵晓敏,黄培清.SM两级闭环供应链系统建模与仿真研究[J].管理科学学报,2011,14(5):29-42.]

[11] WANG Fan, LAI Xiaofan, SHI Ning. A multi-objective optimization for green supply chain network design[J]. Decision Support Systems,2011,51(2):262-269.

[12] HARRIS I, MUMFORD C L, NAIM M M. A hybrid multi-objective approach to capacitated facility location with flexible store allocation for green logistics modeling[J]. Transportation Research Part E:Logistics and Transportation Review,2014,66(1):1-22.

[14] BOUCHERY Y, FRANSOO J. Cost, carbon emissions and modal shift in intermodal network design decisions[J]. International Journal of Production Economics,2015,164(6):388-399.

[15] LI Jin, FU Peihua. Heterogeneous fixed fleet Low-carbon routing problem and algorithm[J]. Computer Integrated Manufacturing Systems,2013,19(6):1351-1362(in Chinese).[李 进，傅培华.具有固定车辆数的多车型低碳路径问题及算法[J].计算机集成制造系统,2013,19(6):1351-1362.]

[16] GAO Juhong, WANG Rui, WANG Haiyan. Closed-loop supply chain network design under carbon subsidies[J]. Computer Integrated Manufacturing Systems,2015,21(11):3033-3040(in Chinese).[高举红,王 瑞,王海燕.碳补贴政策下闭环供应链网络优化[J].计算机集成制造系统,2015,21(11):3033-3040.]

[17] ÖZKLR V, BALLGIL H. Multi-objective optimization of closed-loop supply chains in uncertain environment[J]. Journal of Cleaner Production,2013,41(2):114-125.

[18] SALEMA M I G, BARBOSA-POVOA A P, NOVAIS A Q. An optimization model for the design of a capacitated multi-product reverse logistics network with uncertainty[J]. European Journal of Operational Research,2007,179(3):1063-1077.

[19] RAMEZANI M, BASHIRI M, TAVAKKOLI M R. A new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level[J]. Applied Mathematical Modelling,2013,37(1):328-344.

[20] DEMIREL N, ÖZCEYLAN E, PAKSOY T, et al. A genetic algorithm approach for optimizing a closed-loop supply chain network with crisp and fuzzy objectives[J]. International Journal of Production Research,2014,52(12):3637-3664.

[21] PISHVAEE M S, RABBANI M, TORABI S A. A robust optimization approach to closed-loop supply chain network design under uncertainty[J]. Applied Mathematical Modelling,2011,35(2):637-649.

[22] LIU Baoding, PENG Jin. A course in uncertainty theory[M]. Beijing:Tsinghua University Press,2005(in Chinese).[刘宝碇,彭 锦.不确定理论教程[M].北京：清华大学出版社,2005.]

[23] INUIGUCHI M, RAMLK J. Possibilistic linear programming:a brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem[J]. Fuzzy Sets and Systems,2000,111(1):3-28.

[24] HWANG C L, MASUD A S M. Multiple objective decision making-methods and applications[M]. Berlin, Germany:Springer-Verlag,1979.

[25] MAVROTAS G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems[J]. Applied Mathematics and Computation,2009,213(2):455-465.