基于决策树和模型树的作业工时估计方法

李奇倚，王 磊

(上海交通大学 工业工程系，上海 200240)

0 引言

流程工业包括化工、炼油、冶金和制药等行业，具有较高的自动化程度，并且随着计算机技术、传感器技术和通信技术的发展，流程工业在生产过程中积累了大量的数据，这些数据中隐含着大量的有用信息，然而由于缺少有效的分析工具和高效的计算技术提取有用信息，其数据的价值未被充分利用[1-2]。目前采取的手段是将数据压缩，将短时间段的数据存档，仅在特殊运行状况下进行数据恢复与分析[3]。近年来一些相关研究，如基于数据的调度模型[4-5]和基于数据的关键参数预测方法[6-8]等，证明了从底层数据中挖掘相关的信息和知识并应用于生产决策，可减少决策的不确定性，实现快速分析并减少错误决策的次数[9]。在制造生产中，工时参数是进行生产计划和生产调度的重要依据[6]，被用来确定作业任务量和各个任务的作业时间区间，是计划生产中的关键参数。目前企业主要采用人工粗略估计的方式制定工时，存在费时和准确率低等问题，而基于不准确的工时参数估计生产任务量和作业时间等，会使计划与实际生产有较大偏差，易导致执行脱节[10-11]。基于底层数据的关键参数预测方法是解决该问题的有效手段，因此本文研究基于历史生产数据预估工时参数的方法具有实际意义。

近年来，有关工时预测问题国内外有较多的研究成果：文献[12]采用程序仿真法预测数控加工时间;文献[1,7,13]针对船舶装配工时与航空零件机械加工工时预估问题，采用反向传播神经网络(Back Propagation Neural Network, BPNN)方法，即根据零部件的特征，对相似的零部件分别建立神经网络工时预估模型;文献[14]针对多工位和多夹具加工中心的工时预估问题，采用BPNN方法预测加工工时;文献[8]针对BPNN方法预估精度低的问题，利用基于遗传算法优化的BPNN方法解决化工设备设计工时定量预测问题，并与BPNN及支持向量回归进行了预测效果对比;文献[15]针对船舶生产流程中的工时预估问题，利用分类与回归树(Classification and Regression Tree, CART)方法建立工时预估模型，获得了较好的效果;文献[16]采用CART算法解决制造企业提前期预估问题。然而，大多数研究面向的领域是离散制造业，流程工业因为具有生产连续性的特点，原料和成品多为液体或气体，其加工时间与生产批量之间并非简单的线性关系，而且加工时间还受产品种类、加工者技能熟练程度和作业环境等多种因素影响，所以当前常用的工时预估方法不适用于流程工业中的工时预估问题。

为实现流程工业中生产工时的预测，本文在调研润滑油企业的基础上，首先分析了生产任务分派过程和生产数据的特点，然后针对多品种小批量生产模式且工时受多种因素影响的特点，提出基于决策树[17]和模型树[18]构建工时预估模型的方法。

1 问题描述

因润滑油炼制行业具备流程工业的典型特征，故分析了润滑油企业的生产过程和历史数据的特征，并依此提出需要解决的工时预估问题。

1.1 任务分派中的工时参数

润滑油炼制是将按比例调配好的基础油及催化剂混合在反应釜中进行物化反应的过程，生产过程受操作员熟练程度、天气因素和工艺条件等多因素的影响。

图1所示为任务分派过程，用于解决各生产任务在何时由何种设备、何人操作的问题，其输出结果为短期计划。在该过程中，工时参数用于计算生产负荷，选派合适的设备、人资源，最终确定各个任务的作业时间区间。计划员根据历史生产数据和自身经验制定各产品经济生产批量(Economic Production Quantity, EPQ)下的标准加工时间(Standard Operation Time, SOT)，作为各产品加工工时的标准。在实际生产中，少数产品因批量改变而人工调整炼制时间，其余任务都以SOT作为炼制时间预估值，而这些生产任务中大部分任务的生产批量与EPQ相异，即使某产品以EPQ生产，其实际炼制时间也因生产设备、操作员技能和操作员操作习惯的不同而与SOT相异。因此，当前问题是如何基于现有数据，提供使预估工时能更准确地估算实际任务量的方法。

1.2 数据描述

由数据库中获取的生产数据记录包含6个属性维度，分别为：产品编号(Product No，标称属性)、操作者(Operator，标称属性)、生产批量(Batch，离散数值属性)、反应釜(Kettle，标称属性)、日期(Date，数值属性)、炼制时间(Time，数值属性)。

原始数据中存在噪声数据和不一致数据。噪声最终会导致模型出现偏差，因此在建模前有必要处理掉噪声数据，本文在2.3节利用离群点分析的方法解决该问题;不一致表现为数据记录中的格式不统一,数据经一致化处理后，如表1所示。

表1 预处理后的数据示意

1.3 问题定义

目前需要解决的问题是基于历史数据对炼制时间给出更为精确的估计。炼制时间的直接影响因素有产品种类、生产批量、生产设备、操作者,间接影响因素为日期。因技术提高、工艺改进和环境温湿度变化等潜在因素的影响，炼制时间随着日期的变化呈增长或下降的趋势。

问题的特点有：①产品种类多，不同产品之间存在不同的工时映射关系，而且各产品的历史记录数不均衡(如图2)；②数据集采用混合类型属性描述，输入变量包括标称和数值属性，预测变量为数值属性；③产品炼制时间与生产批量和生产日期之间存在复杂的映射关系，如分段线性关系或不存在显著的线性关系。

记炼制工时为Rt，其与影响因素的关系表示为

Rt=f(Sc(A1,A2,…,Ai),Sn(Ai+1,…,Ak))

=f(A1,A2,…,Ai,…,Ak)。

(1)

式中:Sc表示标称型影响因素的集合，Sn表示数值型影响因素的集合。

研究中，求解模型f的难点在于：①因为产品种类多，且各产品历史记录数不均衡(如图2)，所以人工神经网络方法、多元回归法难以适用；②数据集由混合类型属性描述，因为CART方法使用前需将标称型数据转换为二值型数据，所以无法直接用于解决本问题；③模型f是由多个线性组合构成的映射关系，因其值域非连续的特性而难以直接进行线性拟合；④如何针对各产品建立自身的子模型。在本文背景中，因某些产品的炼制时间与生产批量和生产日期之间并不存在显著的线性关系，若不加处理地将不显著的解释变量加入线性模型，则会导致预测偏差。

在实际问题中需求出两种工时(如表2)，分别记为Rt1和Rt2：

Rt1=f1(p,m,b,d);

(2)

Rt2=f2(p,m,o,b,d)。

(3)

式中p,m,o,b,d分别为产品种类、作业设备、操作员、生产批量和生产日期。

表2 两种工时及考虑因素

3 工时估算方法

因为润滑油产品品种多，生产工时受生产批量、机器、操作员等多种因素影响，不同种类产品存在不同的工时映射关系，所以本文的处理思想为利用众多局部逼近的组合隐含地表示全局目标函数，即首先用决策树构建出各产品所有操作状态的组合，然后用模型树法对各组合依次建立工时映射关系。

工时预估包括模型训练和模型预测两个阶段，如图3所示。

2.1 决策树和模型树

决策树学习采用自顶向下的递归方式构造决策树，以实例为依据，从一组无序、无规则的实例数据中推理出用于决策树形成的分类规则，并根据分类结果进行预测[17]。特征选择是构建决策树的关键步骤，目前的特征选择方法有穷举法、启发式方法和随机法。在使用决策树模型对样本进行分类时，从根节点开始逐步对该样本的属性进行测试，并沿相应的分枝向下行走，直至到达某个叶节点，此时叶节点所代表的类型即为该样本的类型[19]。

模型树是经典CART算法的变体，其训练集需由连续型属性或连续型及二值型属性描述，用于预测连续型的目标变量。针对CART方法，将叶节点设定为常数值的问题，模型树在叶节点处给出某个线性模型，其优势是通过自动优选分段数来拟合非连续、分段线性等问题[20]。模型树算法自提出以来，在众多数值型变量预测问题中证明了其有理想的预测性能，如基于高光谱遥感预测地表生物物理化学参量问题[21]、汽轮机汽耗性预测[22]、有效浪高预测[23-24]、河流污染物纵向分散系数预测[25]、闸下冲刷预测[26]和洪涝灾害预测[27]等。

2.2 模型框架

本文采用决策树和模型树相结合的方法，解决问题的思路是将数据集中的类别型变量和数值型变量分开处理。处理类别型变量问题是一个分类问题，可用决策树方法给出每类的数据集，然后对各类数据集基于模型树法分别给出各类的工时映射关系，最终整个树结构就是整体的工时映射关系，如图4所示。大致过程为：对于混合属性描述的数据集，首先对标称属性用穷举法构建部分树，然后在各分枝上对数值属性用模型树法构建子树，在叶节点处给出线性模型，使该树模型能够用混合属性的数据预测数值型的工时参数。

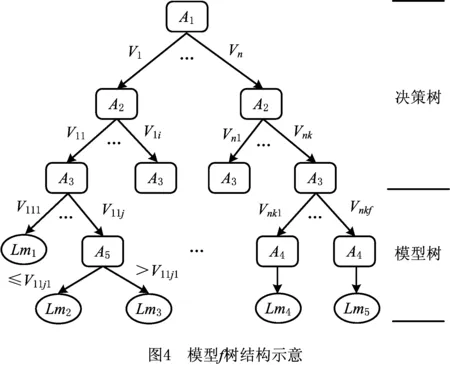
树结构构建分为决策树建树和模型树建树两个阶段。图4中用A1～A5依次表示属性p,m,o,b和d。

2.3 训练算法

获得模型f的关键在于模型训练方法，图5所示为训练算法流程，分为决策树建树阶段(步骤7～8)、回溯操作阶段(步骤10～12)、模型树建树阶段(步骤13)和训练参数选取阶段(步骤3～4，步骤14～16)4个阶段。在训练过程中，只有决策树法和模型树法用于构建树结构模型，回溯操作阶段和训练参数选取阶段用来提升模型的预测精度、提高模型泛化性。

算法中的相关符号说明如下：N为样本量，∂为回溯阈值，θ为切分最少样本数，γ为使用盒图法最少样本数，Bl为内限范围系数，Pis为原始数据集用决策树法划分后所得的所有无节点分枝的集合。

主算法如下：

主算法：main_algorithm。

输入：数据集Dt。

输出：树结构模型。

(1)初始化模型训练参数N，∂，θ，γ和Bl，各自取其最小值。

(2)while训练参数组未遍历完解空间{//遍历所有可选参数值组合

(3)将训练集分成10折，记为FD={Fd1,Fd2,…,Fd10}

(4)for FD中第i折{

(5)train_set={Fd1,…,Fdi-1}∪{Fdi+1,…,Fd10}

(6)test_set={Fdi}

(7)for 属性Aj在序列(A1,A2,A3)中{

(8)用Aj建立节点，并用Aj在train_set所有可能的取值建立分枝}

(9)for 集合Pis中分枝pik{

(10)while pik对应数据集Dik的样本量<∂或未回溯到根节点

(11)回溯操作，并用所处节点的数据集对Dik进行更新

(12)if Dik样本量<∂：生成叶节点，用均值标记

(13)else{子树sub_tree=model_tree(Dik,θ,γ,Bl)；在分枝pik下添加子树sub_tree}

(14)计算模型在第i折上的拟合优度(R2)}//R2计算方法参照式(6)

(15)将10次结果(R2)的均值作为本次训练效果指标并记录}

(17)用得出的较优训练参数组训练模型。

在主算法中，为解决在不同属性描述的数据集上建立模型的问题，采用先对标称属性(A1,A2和A3)基于决策树实现数据集的切分，然后对数值属性(A4和A5)给出用基于模型树构建各段线性关系的方法。对于历史记录不均的问题，在算法中设定了回溯阈值∂，当某类别的数据记录较少时，其能通过回溯操作获得更多相关的数据记录。

(1)决策树建树阶段

决策树建树阶段解决标称属性的划分问题，该阶段依据标称属性的值将数据集划分为多个子集，其过程为：首先在根节点划分属性A1，将各产品类型生成一个分枝；然后在各分枝下生成属性A2节点，在A2上进一步切分各数据子集，再在A3上对各分枝进行更细的切分。在决策树建树阶段指定各层级划分的属性基于以下两点思考：①常用的属性选择度量方法(ID3,C4.5和信息增益等)要求决策目标为类别变量，而文中决策变量为连续型变量，因此这些方法不适用；②本文在决策树阶段属性划分的顺序并不会对模型的预测结果造成影响，而且为便于在各叶节点给出拟合模型，需在决策树阶段完成标称属性的划分。

(2)回溯操作阶段

原有数据集经过多次切分后，某些数据子集的样本量较少，而少量样本无法有效反映某产品炼制工时的规律，容易因过拟合导致模型预测偏差。因此，在算法中设定最少样本数阈值∂，记为回溯阈值。假设当前扫描到分枝pik，则首先判断该分枝对应的数据集包含的样本数，若大于∂，则用pik对应的数据集作为建模数据集；否则向根节点方向逐步回溯，直至当前节点对应数据集的样本量大于∂或到达根节点，并将当前节点对应的数据集作为建模数据集。若回溯步骤因到达根节点而停止，则直接在分枝pik下添加叶节点，并赋予当前数据集的均值。阈值参数的设置在本节训练参数选取阶段中进行详述。

(3)模型树建树阶段

利用A4和A5对各数据子集进行进一步切分,并最终在叶节点处给出某个工时映射关系，用于描述炼制时间与生产批量及生产日期之间的关系。在此过程中需要建立回归模型，然而某些数据子集中自变量与因变量的线性关系不显著，目前常用的解决方法有向前选择法、向后选择法和逐步回归法[28]。因变量个数不多，本文采用向后选择法，设定显著性系数为0.1，通过逐步建模并进行显著性分析选取合适的自变量，对于被剔除的不显著变量，设其回归系数为0。显然，两个自变量都被剔除时，叶节点的值与CART方法中给出的均值相同。

模型树建树方法对应模块model_tree，其为main_algorithm的子模块。model_tree中包含的模块best_split_point用于寻找在A4或A5上的最佳切分点，其中包含regression模块，regression用于线性回归和显著性分析。

模块：model_tree(Dik,θ,γ,Bl)//给出依据数据集Dik得出的子树。

输入：数据集Dik，切分最少样本数θ，盒图法最少样本数γ，内限范围系数Bl。

输出：Dik生成的子树。

(1)集合Set={Dik},temp_set=Set

(2)while(Set非空){

(3)for Set中每个子集Dc{

(4)值v，fik=best_split_point(Dc,θ,γ,Bl)

(5)if 值v非等于None//判断是否存在切分点

(6)用值v切分Dc并将切分后的子集添加到temp_set

(7)else：生成叶节点用fik标记}

(8)从temp_set删除Dc；令Set=temp_set}

(9)Return依据Dik生成的子树

在模块model_tree中有3个关键输入参数，θ用于防止过度切分，γ和Bl为盒图法中的两个参数，它们影响离群点的识别效果。

模型树基于二元切分法，以误差平方和(式(4))作为误差准则，用最大化误差减小(式(5))作为切分点选择方法。

(4)

maxz=SSE(Dc)-SSE(Dpil)-SSE(Dpir)。

(5)

式中：n为样本量，yi为真实值，yi′为预测值，Dc为当前数据集，Dpil和Dpir为在点pi对Dc切分后且用盒图法剔除过噪声对象的两个数据子集，SSE(Dc)表示在Dc上的SSE。当某一节点上的样本集分裂后,目标值变化很小或无法使切分后的数据子集都大于θ时，停止切分并在分枝上添加叶节点，用对应的线性模型标记。

模块：best_split_point(Dc,θ,γ,Bl)//寻找最佳切分点，返回：1 切分点或None；2 regression(Dc,0.1)。

输入：数据集Dc，切分最少样本数θ，盒图法最少样本数γ，内限范围系数Bl。

输出：1 切分点或None，2 regression(Dc,0.1)。

(1)回归参数=regression(Dc,0.1)，可得到y′=fik(A4,A5)，计算SSE

(2)属性A4，A5在Dc中所有可能取值的集合Va4i，Va5i，有值集合Vti=Va4i∪Va5i

(3)for 值pi∈Vti{

(4)用pi划分Dc，划分后利用参数配置为γ和Bl的盒图法剔除噪声点，得到Dpil和Dpir

(5)if Dpil且Dpir的样本数都≥θ{

(6)求得fil(A4，A5)，fir(A4，A5)，并计算err=SSE-SSE(Dpil)-SSE(Dpir)

(7)if err>1：记录err在序列err_list中}

(8)else continue}

(9)if err_list中最大值>1：return该值对应的切分点，fik

(10)Else：return None，fik

对于某产品炼制工时映射关系可能由分段线性关系组合而成的问题，best_split_point模块中通过切分操作来判断是否需用分段线性进行拟合，其中切分最少样本数(θ)用于防止数据集被过度切分。此外，每次切分后，都利用参数配置为γ和Bl的盒图法剔除离群点后再进行拟合(步骤(4))，避免噪声点对拟合造成干扰。

模块：regression(Dc,s_v)//线性回归，返回常数项和回归系数。

输入：数据集Dc，显著系数s_v=0.1。

输出：const，a，b //y=const+ax1+bx2。

(1)自变量集Xs={x1，x2}

(2)While Xs不为空{

(3)用集合Xs中的变量与炼制时间建立线性模型

(4)计算Xs中各变量回归系数的显著性，集合s_t中记录了各变量的显著性系数

(5)If s_t中的最大值>=s_v：剔除对应解释变量

(6)Else{获得const值和回归系数，被剔除自变量回归系数设定为0；break}

(7)If Xs为空{const=Dc中炼制时间均值，且a=b=0}}

(8)Return const，a，b

对于某些产品，生产批量或生产日期与炼制时间并不存在显著的线性关系，模块regression通过向后选择法逐步进行建模，并通过显著性分析选取合适的自变量(步骤(3)～(6))。若在Dc中变量与炼制时间不存在显著关系，则计算Dc中炼制时间的均值(步骤(7))。

(4)训练参数选取阶段

算法中训练的参数有N，∂，θ，γ和Bl，模型对这些参数很敏感。为解决模型参数设置问题，本文采用的方法为：利用全局搜索法，依次用各可行参数组建立模型，并用10折交叉验证法作为模型训练效果的测试方法，以确定性系数R2(式(6))作为评价指标，可得用各参数组建模的评价值集合，最后选出较优参数组用于训练模型。本文设定各参数的取值范围分别为N∈[300,788],∂∈[5,15]，θ∈[5,30]，γ∈[5,30]，Bl∈[0.5,1.5]，其取值范围的确定是基于以下考虑：①通过缩短计算时间来减少算法计算量。②基于经验设定各参数的取值范围，使模型达到较好的预测精度。③拟合时所需的样本量一般为变量数的3～10倍，因此设定最小样本数∂的取值在5～15之间；最小切分数是为保证切分后子集的样本量，因此设定θ在5～30之间；盒图法的内限范围系数Bl常设定为1.5，因为文献[29]论证了该参数的不同取值会直接影响离群点的识别效果，所以本文设定Bl为0.5～1.5，而使用盒图法需满足的最小样本量γ在相关研究中并未有统一的规定，文中给出较为宽松的取值范围，在5～30之间。

(6)

3 方法效果评估

为验证本文所提方法的效果，将某炼油企业获得的828条数据记录随机划分为测试集和训练集两个相互独立的子集，分别包括40条和788条数据记录。因为在实际任务分派中需给出两种工时(Rt1和Rt2)，所以利用训练集依次训练出模型f1和f2，然后在测试集上验证模型效果，本文采用两种方法评估方法效果：①在测试集上对比预估时间和实际时间，计算两者的偏差;②从任务分派层面考虑，将各方法对每日的预估任务负荷量与实际任务负荷量进行比对。

3.1 预估偏差分析

本文采用平均绝对偏差MAD和平均绝对百分比误差MAPE评估方法的预测效果。平均绝对偏差用于评价方法的预估精度，注重反映个体样本上的预测偏差量，其值越小越好；平均绝对百分比误差剔除了单位的影响，是一个无量纲的值，能够反映平均偏离的程度，其值越小越好。

(7)

(8)

式中：n为测试样本数，yi为实际值，yi′为预测值。

表3所示为f1，f2的较优参数在测试集上的预估偏差评价结果。在当前测试集，f1，f2及SOT的MAD分别为0.774，0.752和1.830，MAPE分别为11.94，12.84和32.16，从两个评估指标上来看，本文方法的预估偏差明显低于当前方法，因此在预估精度上，f1和f2均优于SOT。从指标MAD来看，f2相对于f1的预测精度有所提升，但提升幅度不大。

表3 较优训练参数及各自的MAD,MAPE值

图6所示为分别用f1,f2及SOT预测时的偏差折线图，偏差值为预估时间与实际时间之差的绝对值。结合图6，在绝大多数测试样例上，f1和f2的预估偏差都比直接使用SOT要低，而在少数测试样例上出现SOT优于f1，f2的情况，是因为实际生产的偶然性使得在某些时候SOT反而更接近实际炼制时间。而对比f1和f2发现，两模型的预估效果并无显著差异，f2在f1基础上的预估精度提升得并不明显。其原因是：只有部分产品常由不同操作员生产，而在这部分产品中，有些又因生产记录数低于∂进行回溯操作而得到与f1一样的结果。另外，在指标MAPE上，f2的精度低于f1的原因是MAPE容易受到极值的影响。

3.2 预测值与实际值对比分析

图7所示为预测值和实际值的对比图，图中若预测值与实际值完全一样，则点应位于对角线y=x上。这里可用R2评价预测结果的优劣，R2值越接近1，预测效果越好。f1，f2及SOT的R2分别为0.970,0.969和0.957，说明本文方法优于当前方法。

当炼制时间较长时，f2的预测值大多出现在对角线下方，表明其值偏小。而对于绝大部分测试样例，SOT值均位于对角线上方，表明SOT总体偏大。

3.3 日生产负荷量预测分析

在任务分派过程中，会依据工时估算各反应釜每日的任务量，因此本节通过分析对各每日生产负荷量的预测效果来验证所提方法的有效性。

图8所示为各反应釜上每日的实际负荷量以及分别用SOT,Rt1和Rt2预测的结果。可见Rt1及Rt2较为接近实际值，能较好地预估实际任务量，而基于SOT的预估量偏差较大。表4所示为各方法的平均预估偏差率z(式(9))，其值越小表明对日负荷量的预估越精确。

(9)

式中:li为实际负荷量，li′为预测负荷量，wd为该设备的实际生产天数。

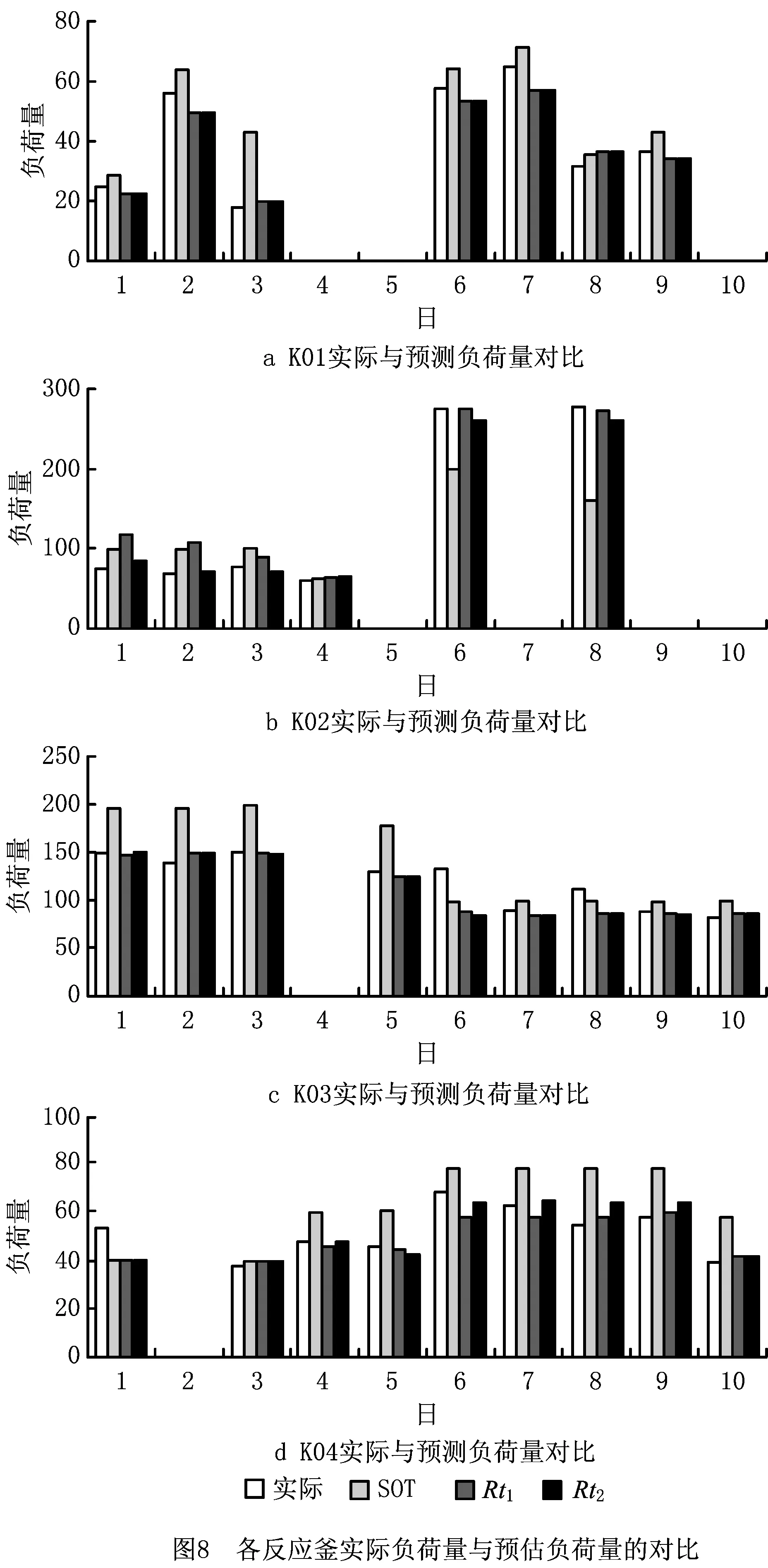
表4 各反应釜日作业任务平均预估偏差率

反应釜K01K02K03K04f19562136867789f2956597870886SOT2724314625622785

在各反应釜上，本文方法在日任务平均预估偏差率上均优于当前方法，且基本都在10%的偏差范围内，因此在任务量预估精度上，本文方法优于当前的预估方法。此外，在K02上发现SOT预估效果较差，原因是某些产品类型的炼制时间变化较大，SOT因更新不及时而无法有效反映当前生产状态。

4 分析讨论

为了探究训练参数对预测精度的影响程度，以及训练参数选取阶段的必要性和有效性，本章通过敏感度分析给出各参数的影响程度，然后给定不同训练集讨论训练参数选取的效果。

4.1 敏感度分析

算法中有训练参数N，∂，θ，γ和Bl，模型对这些参数很敏感。下面分析各个参数取值的变化对预测精度的影响,以及各参数对预测精度的影响程度。

4.1.1 训练参数变化对预测精度的影响

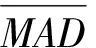
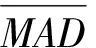
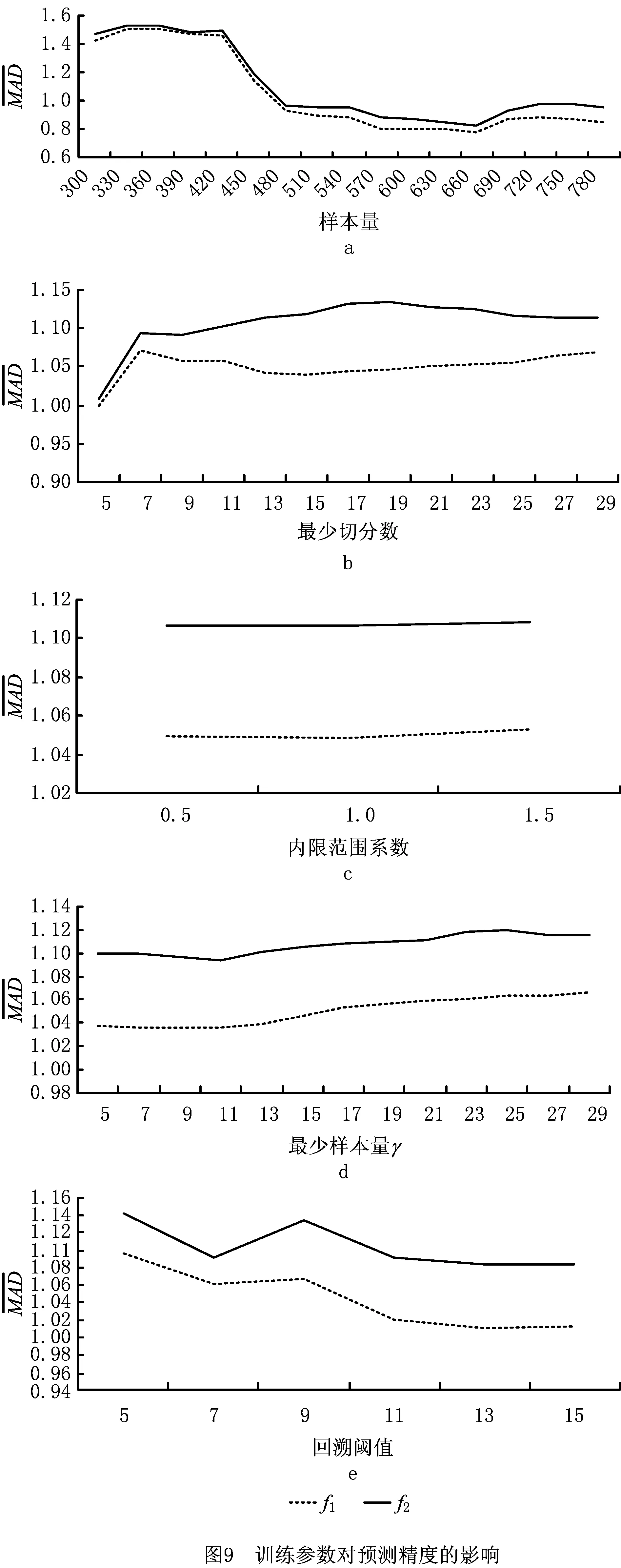
图9b中当最少切分数从5变化到7时，预测精度出现了明显的下降，可能是因较多产品的历史记录数在10～13范围内，取值为5可进一步切分而有更好的拟合效果。之后，随着最少切分数的增加,f1和f2预测精度的变化不是很明显。

图9c和图9d给出了盒图法中两个参数变化对预测精度的影响。图9c中内限范围系数只有3个取值，可能因取值少而使不同内限范围系数的预测精度区别不大。图9d显示，随着γ的增加，预测精度先提高，然后呈现下降的趋势，原因是当前各类产品的样本量并不多，γ越大，因样本量不够而未进行去噪操作的子集越多，因此直接拟合会导致预测精度降低。

4.1.2 训练参数方差分析

为探究各参数与预测精度的相互关系，并量化各参数对结果的影响程度，目前常用的方法为方差分析法[30-32]，本文设定显著性水平为0.05。由于包含5个参数，且各参数的水平数不等(如Bl有3种水平，分别是0.5,1.0和1.5)，这里采用方差分析中的一般线性模型，结合Minitab软件进行计算分析。

表5和表6所示为各参数的连续平方和(Seq SS)、调整的平方和(Adj SS)、调整均方(Adj MS)、F统计量及其P值。

表5 f1训练参数方差分析表

表6 f2训练参数方差分析表

在表5和表6中，各参数对应的P值都小于给定的显著性水平0.05，表明每个训练参数都对f1和f2的预测精度有显著影响，但影响程度不同。对于f1，参数样本量(N)的F统计量最大，为主要影响因素，其次为回溯阈值(∂)，然后为最少切分数(θ)，再次为最少样本量(γ)，最后为内限范围系数(Bl)，各参数按影响程度高至低排列依次为N—∂—θ—γ—Bl;对于f2，各参数按主次顺序排列为N—θ—∂—γ—Bl。在f2中，影响程度有所增强的有∂,θ。因为在f2中比f1多考虑了工人因素，所以决策树划分后，各子集所包含的样本数更少，在回溯操作阶段常需进一步判断处理，而回溯阈值作为是否回溯操作的判断标准，更易影响f2的预测精度。类似地，若最少切分数较大，则部分较小子集还未切分就直接给出了叶节点，因此样本数偏小的子集的θ取值更难权衡，从而使θ对f2的影响更为显著。

综上可知，训练参数对模型的预测精度都有显著的影响,对于f1和f2而言，样本量均为影响最为显著的训练参数。f2相对于f1，因多考虑了操作员因素，其预测精度更易受到参数取值的影响。因此在实际中，若有模型f3考虑了更多影响因素，则可能使模型的效果更加不稳定，但在训练参数取值合适时，其效果优于考虑因素较少的模型，而当参数变动时，其预测精度将出现较大波动。

4.2 训练集规模约束下训练参数的优化

本文收集的数据是一个时段的数据记录，而实际中的数据是变化的，且随生产不断积累。为了解训练集规模不一致时本文方法的效果，以及参数选取阶段对预测精度所起的作用，给出两组训练集，训练集1包括788条数据记录，训练集2包括540条数据记录，两者的测试集相同。同样以MAD和MAPE作为效果评价指标。

两组训练集分别用于训练，给出的较优参数如表7所示。对于训练集1，基于较优训练参数建立的f1和f2在测试集上的MAD分别为0.774和0.752，MAPE分别为11.94和12.84，而对于该测试集，若训练样本量相同，则其能达到的最优效果分别为MAD=0.628,0.600，MAPE=10.66,11.37，当参数取值N=330,∂=12,Bl=1.5,γ=9,θ=5时，求出的f1预估精度最低，为MAD=1.741；当参数取值N=360,∂=5,Bl：1.5,γ=23,θ=5时，求出的f2预估精度最低，为MAD=1.715。将本文方法的预估精度与在各种训练参数下所得模型的预测精度进行对比，本文方法的预估精度所处的分位值为f1=13.77%，f2=1.54%，即f1的预估精度超过了所有可取参数组中86.33%的对象，f2的预估精度超过了所有可取参数组中98.46%的对象。对于训练集2，本文方法的预估精度所处的分位值为f1=4.25%，f2=9.62%。因此，本文方法能够有效找出较优训练参数。

表7 在不同训练集上的训练参数和方法效果

续表7

当给定的数据集不同时，本文方法给出的训练参数也有差异。在训练集1上，给出的需求训练样本量小于全部样本量，而在训练集2上，给出的需求训练样本量等于全部样本量，且样本量较多时的模型效果明显优于样本量较少时模型的效果，表明要获得更高的预测精度需要保证足够量的样本量用于训练。此外，将f1和f2建立模型时所需的样本量和预测精度进行对比发现，若样本足够，则f2可达到比f1更高的预测精度，且所需的样本量多于f1，样本量对f2预测精度的影响更加显著。因此在实际中，若样本数据较少，则可尝试选用模型f1，以期得到更好的效果。

综上，本文方法能够找出较优训练参数，其给出的参数有一定的参考价值，当数据量变化时，本文方法有一定的适应能力。因条件限制，当前方法并未在大样本集上进行测试分析，当数据量较多时，该方法的效果还需进一步验证。

文中采取十折交叉验证的方法来避免过拟合，提高模型的泛化性，虽然在十个不同的折上验证了模型的效果，但仍不可避免地存在抽样误差。因此，在实际中为获得更加稳定的效果，可在给定数据集上多次运行该算法，并人工对训练参数进行挑选。

5 结束语

本文针对流程工业任务分派过程中存在的问题,提出基于决策树和模型树的工时估算方法,该方法适用于较小的训练样本集，能够结合标称值和数值变量来预估作业时间。在实例分析中，采用某润滑油炼制企业的实际数据建立了两种工时估算模型，相对于用SOT预估时32.2%的误差，本文模型可使实做工时与预估工时的误差保持在12.8%以内，预估工时在任务分派过程中能够更准确地预估实际任务量，用于进一步优化设备和操作员资源配置。

目前方法中并未考虑离群点的产生机制及可能的含义，且在低维空间剔除离群点时因忽略了某些情境属性，可能导致错误识别和部分离群点被正常对象掩盖。本文在参数选取阶段用所有可能的参数组建模，然后挑选出较优的训练参数，存在训练时间过长的问题。未来将针对这两点作进一步研究，以提高预估模型的进度并减少模型训练时间。

[1] WU Xindong, ZHU Xinquan, WU Gongqiong, et al. Data mining with big data[J]. IEEE Transactions on Knowledge & Data Engineering,2014,26(1):97-107.

[2] SYED A R, GILLELA K, VENUGOPAL C. The future revolution on big data[J]. Future,2013,2(6):2446-2451.

[3] LIU Qiang, QIN Sizhao. Perspectives on big data modeling of process industries[J]. Acta Automatica Sinica,2016,42(2):161-171(in Chinese).[刘 强,秦泗钊.过程工业大数据建模研究展望[J].自动化学报,2016,42(2):161-171.]

[4] LIU Min, HAO Jinghua, WU Cheng. A prediction based iterative decomposition algorithm for scheduling large-scale job shops[J]. Mathematical & Computer Modelling,2008,47(3):411-421.

[5] GRADISAR D, MUSIC G. Production-process modelling bas-ed on production-management data:a Petri-net approach[J]. International Journal of Computer Integrated Manufacturing,2007,20(8):794-810.

[6] LIU Bin, JIANG Zuhua. The intelligent man-hour estimate technique of assembly for shipbuilding[J]. Journal of Shanghai Jiaotong University,2005,39(12):1979-1983(in Chinese).[刘 滨,蒋祖华.船舶装配作业工时智能估算技术[J].上海交通大学学报,2005,39(12):1979-1983.]

[7] SHEN Ling, ZHANG Zhiying. Research on the work quota estimation method for ship iron outfitting pieces[J]. Industrial Engineering & Management,2011,16(4):96-102(in Chinese).[沈 玲,张志英.船舶铁舾件工时定额估算方法研究[J].工业工程与管理,2011,16(4):96-102.]

[8] DAI Jianwei, JI Hua, YANG Gang, et al. Man-hour forecast model based on GA_BP for chemical equipment design[J]. Computer Integrated Manufacturing Systems,2013,19(7):1665-1675(in Chinese).[戴健伟,吉 华,杨 岗,等.基于GA_BP算法的化工设备设计人工时预测[J].计算机集成制造系统,2013,19(7):1665-1675.]

[9] OBITKO M, JIRKOVSKY V, BEZDICEK J. Big data challenges in industrial automation[C]//Proceedings of International Conference on Industrial Applications of Holonic and Multi-Agent Systems. Berlin, Germany:Springer-Verlag,2013:305-316.

[10] LI Li, SUN Zijin, NI Jiacheng, et al. Data-based scheduling framework and adaptive dispatching rule of complex manufacturing systems[J]. The International Journal of Advanced Manufacturing Technology,2013,66(9/10/11/12):1891-1905.

[11] LI Qiyi, WANG Lei, XU Jingjing. Production data analytics for production scheduling[C]//Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management. Washington, D.C.,USA:IEEE,2015:1203-1207.

[12] COELHO R T, DE SOUZA A F, ROGER A R, et al. Mechanistic approach to predict real machining time for milling free-form geometries applying high feed rate[J]. The International Journal of Advanced Manufacturing Technology,2010,46(9/10/11/12):1103-1111.

[13] LI Yajie, HE Weiping, DONG Rong, et al. Man-hour forecasting and evolution based on MES data collection[J]. Computer Integrated Manufacturing Systems,2013,19(11):2810-2818(in Chinese).[李亚杰,何卫平,董 蓉,等.基于制造执行系统数据采集的工时预测与进化[J].计算机集成制造系统,2013,19(11):2810-2818.]

[14] DONG Qiaoying, LU Jianshan, KAN Shulin. A study on man-hour calculation model for multi-station and multi-fixture machining center[J]. Advances in Intelligent and Soft Computing,2012,149:403-411.

[15] HUR M, LEE S K, KIM B, et al. A study on the man-hour prediction system for shipbuilding[J]. Journal of Intelligent Manufacturing,2015,26(6):1267-1279.

[16] OZTRK A, KAYALGIL S, OZDEMIREL N E. Manufacturing lead time estimation using data mining[J]. European Journal of Operational Research,2006,173(2):683-700.

[17] QUILAN J R. Induction of decision trees[J]. Machine Learning,1986,1(1):81-106.

[18] QUILAN J R. Learning with continuous classes[C]//Proceedings of Australian Joint Conference on Artificial Intelligence. Singapore:World Scientific,1992:343-348.

[19] GUAN Xiaoqiang. Research on the classifying Algorithm based on decision tree[D].Taiyuan: Shanxi University,2006(in Chinese).[关晓蔷.基于决策树的分类算法研究[D].太原:山西大学,2006.]

[20] WANG Yong, WITTEN L. Induction of model trees for predicting continuous classes[M]. Prague, Czechoslovakia: Faculty of Informatics and Statistics,1996.

[21] WANG Yuanyuan, CHEN Yunhao, LI Jing. Application of model tree and support vector regression in the hyperspectral remote sensing[J]. Journal of China University of Mining & Technology,2006,35(6):818-823(in Chinese).[王圆圆,陈云浩,李 京.模型树和支持向量回归在高光谱遥感中的应用[J].中国矿业大学学报,2006,35(6):818-823.]

[22] ZHANG Jianmin, LIU Dengtao, WU Guangzhong, et al. Working condition characteristics identification for extraction unit by using M5’ model tree and measured data[J]. Proceedings of the CSEE,2011,31(23):21-26(in Chinese).[章坚民,刘登涛,吴光中,等.采用M5’模型树和测量数据识别抽汽式机组汽耗量特性[J].中国电机工程学报,2011,31(23):21-26.]

[23] ETEMAD SHAHIDI A. Predicting longitudinal dispersion coefficient in natural streams using M5’ model tree[J]. Journal of Hydraulic Engineering,2012,138(6):542-554.

[24] BONAKDAR L, ETEMAD SHAHIDI A. Predicting wave run-up on rubble-mound structures using M5 model tree[J]. Ocean Engineering,2011,38(1):111-118.

[25] ETEMAD SHAHIDI A, MAHJOOBI J. Comparison between M5′ model tree and neural networks for prediction of significant wave height in lake superior[J]. Ocean Engineering,2009,36(15):1175-1181.

[26] GOYAL M K, OJHA C S P. Estimation of scour downstream of a ski-jump bucket using support vector and M5 model tree[J]. Water Resources Management,2011,25(9):2177-2195.

[27] SINGH K K, PAL M, SINGH V P. Estimation of mean annual flood in Indian catchments using backpropagation neural network and M5 model tree[J]. Water Resources Management,2010,24(10):2007-2019.

[28] MONTGOMERY D C, PECK E A, VINING G G. Introduction to linear regression analysis[M]. New York, N.Y.,USA:John Wiley & Sons,2015.

[29] FRIGGE M, IGLEWICZ B. Some implementations of the boxplot[J]. American Statistician,1989,43(1):50-54.

[30] GUAN Wenjiang, CHEN Xinjun. Fishing efficiency for mac-

kerel and scad in the large light purse seine fishery estimated by generalized linear model[J]. Journal of Fisheries of China,2009,33(2):220-228(in Chinese).[官文江,陈新军.应用一般线性模型估算鲐、鲹大型灯光围网渔业的捕捞效率[J].水产学报,2009,33(2):220-228.]

[31] HU Xiaosu, HONG K S, GE S S, et al. Kalman estimator-and general linear model-based on-line brain activation mapping by near-infrared spectroscopy[J]. Biomedical Engineering Online,2010,9(1):82.

[32] THORNTON R C, RODIONOV R, LAUFS H, et al. Imaging haemodynamic changes related to seizures:comparison of EEG-based general linear model, independent component analysis of fMRI and intracranial EEG[J]. Neuroimage,2010,53(1):196-205.