不确定条件下航空发动机大修周期预测方法
2018-03-19贾晓亮
陈 振,贾晓亮
(西北工业大学 现代设计与集成制造技术教育部重点实验室,陕西 西安 710072)
0 引言
作为现代工业“皇冠上的明珠”,航空发动机的研制难度极高,其大修过程也异常复杂,有很高的技术含量。航空发动机大修是指按照技术标准对发动机进行全面恢复技术状态的修理,是航空发动机最高等级、技术最复杂的修理[1]。由于航空发动机结构复杂,每一台航空发动机由于其本身的技术质量状态、零部件损伤形式/损坏程度、维修资源以及维修差错等存在不确定性,常使大修周期呈现出不确定波动,大大增加了大修周期预测的难度,若大修周期的不确定波动过大,会降低生产效率、影响生产进度,因此有必要对航空发动机大修周期进行准确预测,为航空发动机大修进度控制与工艺流程优化提供科学依据。
航空发动机大修是一个计划性非常强的复杂项目,减少大修周期、预测大修生产瓶颈、降低大修成本是大修工艺流程优化的目标。计划评审技术(Program Evaluation and Review Technique, PERT)常用于复杂项目进度管理中,是进行项目工期预测、评价项目进度的有效方法。余芬等[2]利用PERT构建B747飞机大修流程网络图,计算了网络图中的工序时间参数,并利用削峰法对大修流程进行了人员优化;马晓乐等[3]以飞机大修厂的批次进度为数据,结合大修工艺路线和作业进度,利用PERT确定整机大修的关键路径和总工期;Atli等[4]对传统PERT方法进行了改进,用模糊数表示工序持续时间,提出运用模糊关键路径法构建航空发动机大修流程网络图,根据模糊数运算规则计算修理活动时间,得出航空发动机大修流程的关键路径与模糊周期;李成川等[5]针对工艺路线不确定性问题,建立了基于图形评审技术的工艺路线模型,该模型可以很好地描述再制造工艺路线的不确定性特点;杨铭等[6]针对传统PERT方法的不足,提出一种改进的PERT对航空项目进行风险评价,有效提高了航空项目风险评价的可靠性。然而,实际的航空发动机大修过程是以出现耗损的零部件为对象,质量状态的高度不确定性是其主要特点[7],这些不确定性因素对大修周期的影响虽然难以显式表达,但都隐含在大修过程各项作业的持续时间中,导致大修过程中实际修理时间分布规律的不确定性[8],因此在使用传统PERT方法分析航空发动机大修周期和关键线路时必然会产生较大的偏差。近年来,一些学者提出新的工期预测建模方法。汤新民[9]将Petri网建模分析技术引入航空发动机维修车间的服务能力评价中,揭示了影响航空发动机车间维修进度的瓶颈工段;李聪波等[10]针对工艺时间不确定性问题,提出一个废旧零部件不确定性再制造工艺时间的模糊学习系统,基于废旧零部件的质量状况信息对其工艺时间展开模糊学习;朱海平等[11]在分析影响产品完工期的不确定因素的基础上,利用神经网络集成方法对产品完工期建立预测模型,实现了对预测结果的点估计和区间估计;Li等[12]研究了装配时间不确定条件下,复杂装配件装配完工时间的求解方法。然而,这些方法所构建的模型十分复杂,所需样本数据量较大,难以应用在航空发动机大修这种“多品种、小批量”生产模式中。
蒙特卡洛(Monte Carlo, MC)方法作为处理不确定性问题的典型方法,自提出以来,在不同领域得到了一定的应用与发展。王利明等[13]将蒙特卡洛方法应用到装备保障方案评估方面,综合考虑工序逻辑约束、保障车辆约束和飞机部件可靠性等因素的影响,得到不同因素对保障工作及时性的影响程度;在施工进度仿真领域中,钟登华等[14]通过构建不同施工工序相应的工时概率分布模型,运用蒙特卡洛仿真技术得出施工工期的统计分布、关键路线和工序关键度,为施工进度控制奠定了基础。
综上所述,目前国内外学者已经开展了关于复杂装备大修、再制造等这类以不确定性为主要特点的过程系统研究,主要集中在零部件的工艺路线优化、工艺时间计算、大修网络图等方面,对不确定条件下航空发动机大修周期的预测研究鲜有涉及;另外,蒙特卡洛方法作为一种研究不确定性问题的方法,在其他工程领域得到了研究与应用,但对航空发动机大修周期的预测还未见报道。
航空发动机大修过程的众多不确定性因素,使得大修周期预测比传统制造过程周期的预测更为复杂,而大修周期对航空发动机大修进度控制和工艺流程优化有非常重要的影响,因此亟需开展不确定条件下航空发动机大修周期准确预测方法的研究。本文将综合考虑航空发动机大修过程的相关不确定性因素,开展航空发动机大修周期准确预测方法的研究。首先对航空发动机大修周期不确定性问题进行描述,在此基础上提出一种融合PERT和蒙特卡洛仿真的预测方法,通过得到的航空发动机大修周期概率分布、关键线路和工序关键度进行大修周期的准确预测,为航空发动机大修进度控制和精细化管理提供依据。
1 航空发动机大修周期预测不确定性描述
航空发动机结构复杂,大修过程中要将航空发动机彻底分解,分解的零部件要进行相应的检查、修理或更换[9]。由于零部件的技术质量状态、损伤形式、损坏程度、维修资源和维修差错等不确定因素的影响,每一项大修工序的实际完成时间是不确定的,从而导致整个大修周期不确定。
与航空发动机的制造过程相比较,其大修过程有以下特点:
(1)工艺路线的不确定性 航空发动机大修时,其零部件的修理工艺路线具有不确定性[15]。一般情况下,航空发动机制造中针对零部件的制造过程有确定的工艺路线,而在大修过程中待处理的多是出现耗损的零部件,零部件的工艺路线由很多因素决定,如零部件的损坏形式、损坏程度和航空发动机的质量状态条件(健康状况、航空发动机服役时间及维修后的整机状况),这些因素最终导致航空发动机的大修工艺路线不确定,不确定性是这类系统面临的最大挑战[16]。
(2)工序时间的不确定性 航空发动机大修过程中的另一个特点是工序时间的不确定性。与航空发动机的制造过程相比,大修时间具有更大的不确定性。因为零部件损伤状况的不同会导致大修工艺路线的不确定,而不同的大修工艺路线对应的大修时间也不同,所以不同损伤程度的零部件在大修过程所需的大修时间会有很大不同。
由以上分析可知,航空发动机大修周期预测是受航空发动机技术质量状态、故障出现形式及程度、维修工艺路线和工艺时间等不确定性因素影响的复杂不确定性问题。
传统PERT方法求解工期不确定性问题的理论基础是假定工序持续时间服从β分布,并且用三时估计得到的期望和方差来代替β分布的期望和方差,最后将不确定型网络转化成确定型网络来计算。该方法的局限性在于:首先,复杂航空装备大修活动的持续时间不一定均满足β分布;此外,将不确定型网络当作确定型网络来计算,得到的期望时间偏小,并且只得到一条关键线路,忽视了非关键线路上的大修活动对完工概率的影响。
针对传统PERT方法的局限性,本文提出的融合PERT和蒙特卡洛方法具有如下优势:
(1)航空发动机大修工序时间的概率分布不再统一假设服从β分布,而是根据实际情况统计得到大修工序的时间概率分布。
(2)利用蒙特卡洛抽样技术对大修工序持续时间进行随机抽样,抽样次数越多,得到的结果越准确,从而避免了传统PERT网络繁琐的计算,而且每次仿真计算的时间参数都不同,得到的关键线路不止一条,关键活动也会发生变化,从而可以预测关键线路及关键活动的分布情况。
(3)定义了航空发动机的大修工序关键度,航空发动机大修决策者可以依据这两个指标确定需要重点关注的大修活动,从而为航空发动机大修决策提供实际指导。
2 不确定条件下航空发动机大修周期预测建模
在航空发动机大修工艺流程中,由于工序时间和工艺路线都具有不确定性,本文提出一种融合计划评审和蒙特卡洛仿真的方法进行大修周期求解,该方法是在传统PERT的基础上,融入蒙特卡洛仿真对不确定性变量进行模拟,可以很好地解决不确定条件下的航空发动机大修周期预测问题。
2.1 不确定条件下航空发动机大修工序逻辑关系
航空发动机大修工序逻辑关系指航空发动机大修工序之间的依赖和相互关系,并根据这种逻辑关系安排各项活动的先后顺序。为便于模型构建,本节将复杂的逻辑关系分类为4种,并抽象成相应的网络图,网络图中的每个节点表示一个大修活动,如图1所示。抽象后的网络图表达简单直观,便于数学求解。

(1)串行关系 是大修流程中最简单的逻辑关系,其中各大修工序按顺序依次进行,前一个大修工序完成是下一个大修工序开始的必要条件。
(2)并行关系 并行关系中的各工序可以同时开始,并且这些工序均完成后才能进行下一道大修工序作业。
(3)汇聚关系 指两个或多个紧前大修活动完成后才能进行下一道工序作业的情况,这种情况在单元体装配或整机总装中最常见。
(4)发散关系 指某一道工序完成后,可以有两个或多个紧后大修工序同时作业的情况,这种情况在单元体分解工序中最常见。
2.2 不确定条件下航空发动机大修工序时间参数描述
PERT[17]是一种以时序网络为基础的计划和调度方法,主要用于具有不确定性因素的项目/工程管理分析。PERT网络中的时间参数主要包括最早开始时间(ES)、最早完成时间(EF)、最迟开始时间(LS)、最迟完成时间(LF)、总时差(TF)和自由时差(FF),总时差为零的工序即为关键工序,由关键工序连接的从起点节点到终点节点的线路为关键线路。以i表示网络图中某一大修工序,h表示工序i的紧前工序,j表示工序i的紧后工序,Di表示工序持续时间。工序的时间参数计算如下:
ESi=max{ESh+Di};
(1)
EFi=ESi+Di;
(2)
LSi=min{LSj-Di};
(3)
LFi=LSi+Di;
(4)
TFi=LSi-ESi=LFi-EFi;
(5)
FFi=ESj-EFi。
(6)
传统PERT方法假设工序持续时间服从β分布,然而航空发动机大修受多方面不确定性因素的影响,大修工序的持续时间具有很强的随机性,即式(1)~式(4)中的Di服从不同概率分布类型,应根据实际大修生产数据确定。
蒙特卡洛方法也称随机模拟方法或随机抽样技术,由美国曼哈顿工程的成员John von Neumann和Stanislaw Ulam率先于20世纪40年代提出,当时主要用于核聚变的研究。蒙特卡洛方法可以对服从任意分布的随机变量进行抽样,从而很好地解决航空发动机的大修工序持续时间不确定性问题。本文采用蒙特卡洛方法对Di进行随机抽样,其流程如图2所示。
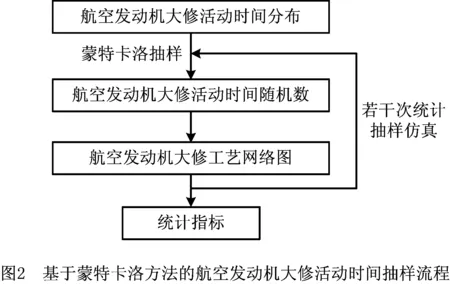
从每个航空发动机大修工序时间的概率分布中随机抽取一个值,表示一个输入变量,定义为一种随机数,将其代入式(1)~式(6),得到相应的输出值,即大修周期样本值。整个过程重复计算n次,得到n个随机数,相应地得到n个大修周期样本值。
2.3 不确定条件下航空发动机大修周期预测模型
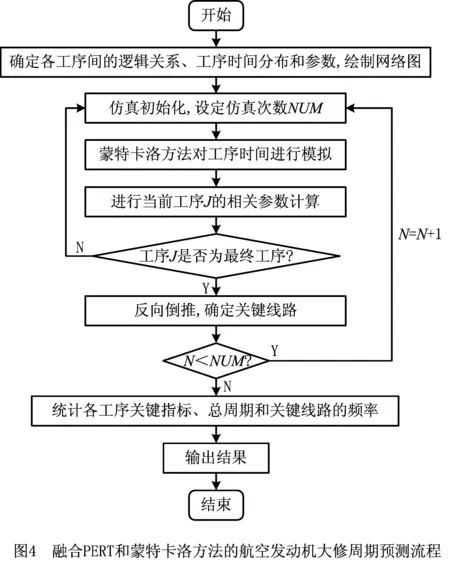
航空发动机大修过程由一系列单元体大修组成,每个单元体大修又包括零部件的清洗、检测、修理等工序。由于待修航空发动机技术质量状态不同,如服役时间、健康状况及上次维修后的状况,导致航空发动机大修工作范围多变,大修工序之间的逻辑关系复杂,工序时间的不确定性较大。因此,要准确预测航空发动机大修周期,既需要分析大修过程中大修工序的逻辑关系,又要分析大修工序时间的不确定性。如图3所示为所建立的航空发动机大修周期预测模型,其模型构建的一般步骤为:
(1)根据航空发动机大修工艺流程规程,将工艺流程中的大修活动抽象为网络节点,根据大修活动之间的逻辑关系建立航空发动机大修工艺流程网络图。
(2)根据航空发动机大修活动分解后得到的大修工艺路线不确定性分析数据和历史数据,建立航空发动机大修活动持续时间概率分布。
(3)运用融合PERT和蒙特卡洛仿真方法对模型进行求解及不确定性分析。

3 融合PERT和蒙特卡洛方法的航空发动机大修周期预测
融合PERT和蒙特卡洛方法进行航空发动机大修周期预测就是在蒙特卡洛仿真的基础上,综合PERT技术寻求关键路径与关键工序[18-20],探寻航空发动机大修周期的分布规律,在全面掌握关键线路分布情况的基础上,更加准确地描述航空发动机大修过程的不确定性,从而实现航空发动机大修周期的准确预测。
3.1 基本概念
定义1航空发动机大修周期。指航空发动机大修从入场经过故检、分解、修理等工艺流程到试车出厂所经历的时间周期,大修周期具有高度不确定性,通过一次仿真可以得到该仿真条件下的一个大修周期,对所有仿真得到的大修周期进行统计,可以得到航空发动机大修周期的分布规律及完工概率。
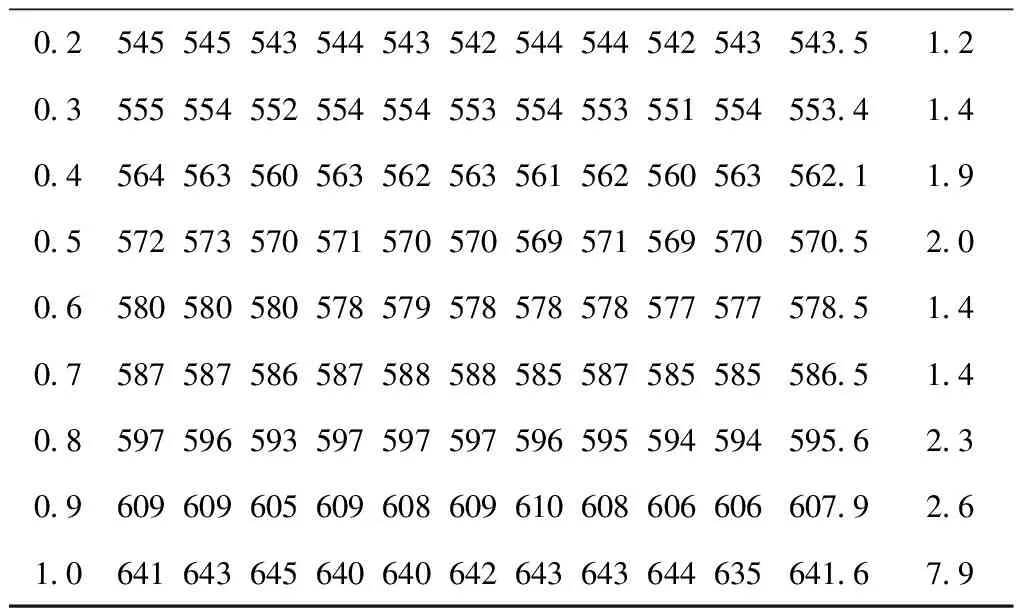
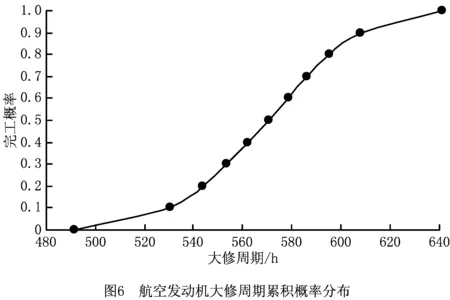
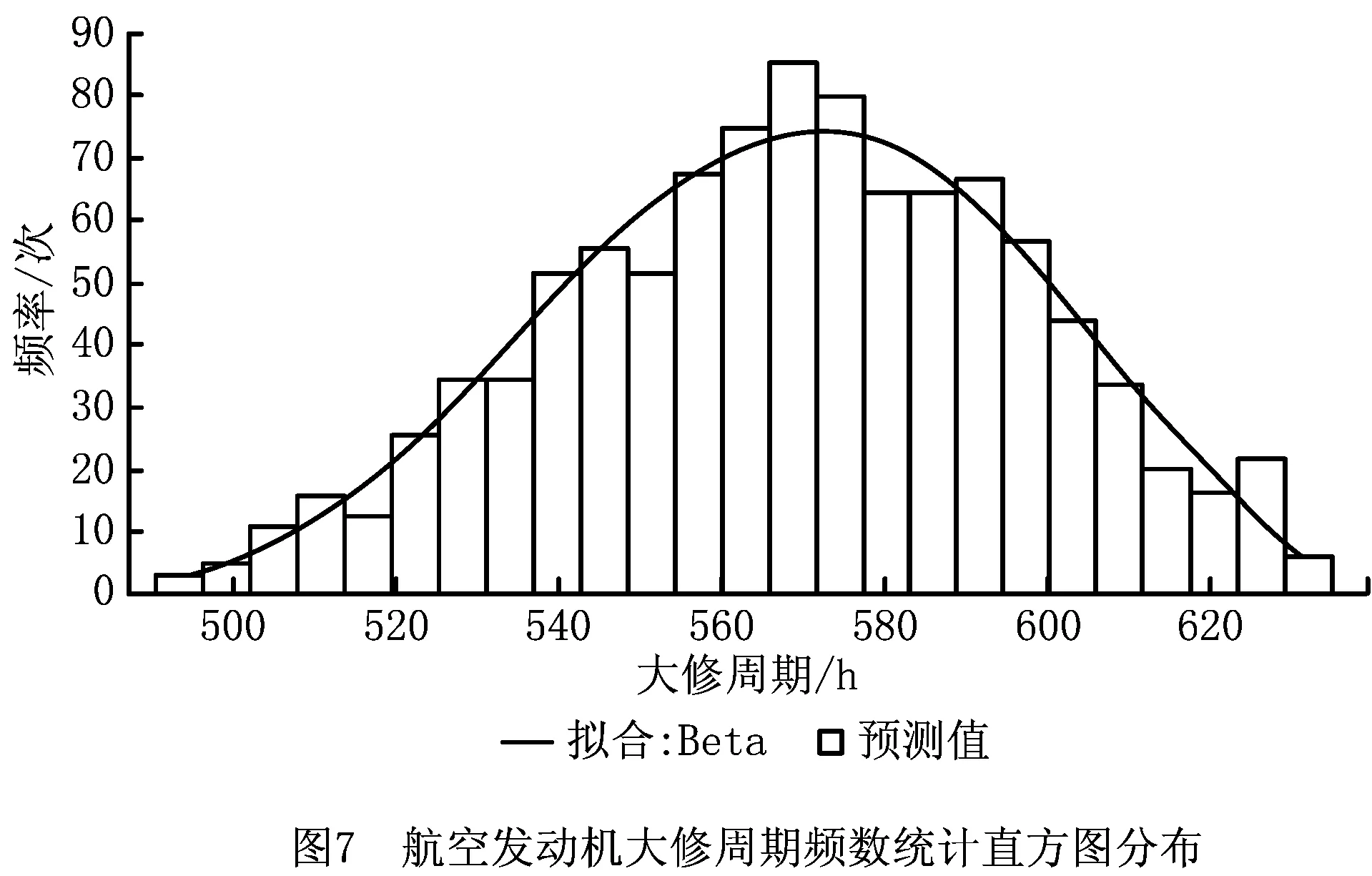
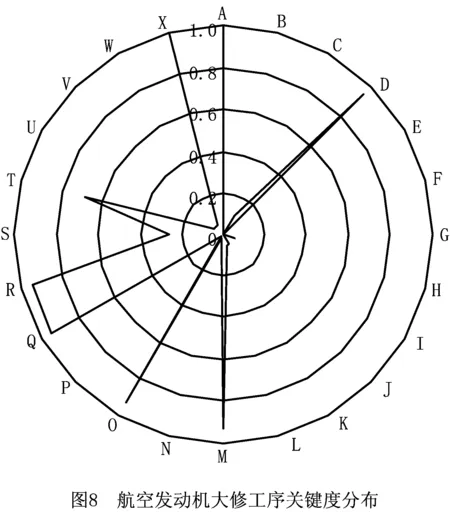
定义2线路关键概率。指某一大修工艺路线为关键线路的概率。设N次模拟中网络中共出现了r条关键线路,分别用l1,l2,…,lr表示,关键线路出现的频数分别为m1,m2,…,mr(r PCPi=mi/N(1≤mi≤N,1≤i≤r, 0≤PCPi≤1)。 (7) 定义3工序关键度(Activity Critical Degree, ACP)。在PERT网络中,采用蒙特卡洛方法对工序i时间模拟N次,统计N次模拟条件下工序i落在关键路线上的次数,记为Mi,则工序i的关键度A=Mi/N。 定义4仿真关键线路指多次仿真运行中成为关键线路次数最多的线路。 工序关键度和线路关键概率可以通过蒙特卡洛仿真得到。航空发动机大修过程中通过控制工序关键度较大的工序,可以有效控制大修生产进度,降低大修周期的不确定性。 蒙特卡洛仿真是通过构建随机变量的概率模型,利用蒙特卡洛方法对概率模型进行抽样实验,并用实验结果作为求解结果的一种仿真方法。因此,随机变量概率分布模型的构造以及抽样公式的选择是影响仿真结果的决定性因素。 已有研究指出,随机变量概率分布的构建可先根据先验知识对该工序的实际内容和在整个工艺过程中的作用进行定性判断,确定其可能属于哪几种分布类型,然后再进一步分析,逐步缩小选择范围。若某项工序由大量简单重复作业组成,则可判定该工序时间服从正态分布。航空发动机大修工序时间常见的概率分布有正态分布和三角分布[14],其抽样公式分别如下: (1)正态分布抽样公式 工序时间满足正态分布的抽样公式为 (8) 式中:xi为正态分布随机抽样时间;μ为期望值;σ为均方差;r1,r2为[0,1]区间上均匀分布的一对伪随机数。 (2)三角分布抽样公式 工序时间满足三角分布的抽样公式为 xi= (9) 式中:xi为三角分布随机抽样时间;a,b,m为三点估计值;ri为[0,1]区间上的伪随机数。 综上所述,融合PERT和蒙特卡洛方法的航空发动机大修周期预测过程如下: (1)根据航空发动机大修工艺流程要求确定大修工序逻辑关系,绘制航空发动机大修流程网络计划图。 (2)确定各工序的概率分布类型并给出分布参数,计算仿真次数NUM,本文利用文献[11]中的方法确定仿真次数。 (3)根据各工序的概率模型及具体参数进行一次模拟,产生符合相应工序概率模型的随机数。 (4)每一次仿真运行中,根据(3)得到的随机数用PERT算法计算各工序的时间参数,根据输出值确定本次仿真条件下航空发动机大修周期、关键线路等网络参数。 (5)重复(4)的过程,直到仿真次数达到NUM。 统计NUM次仿真结果,可以得到大修周期的频率分布以及各工序在关键线路上的频次,得到航空发动机大修周期概率分布、关键线路和关键工序,其仿真模拟流程如图4所示。 某大修厂新承担某型航空发动机的大修工作,由于该航空发动机使用时间较长,零部件受损情况复杂,导致大修工艺流程十分复杂,涉及的工序繁多,工序之间逻辑关系复杂,大修厂亟需了解改型航空发动机大修周期的分布规律以及关键线路的规律,从而进行有效的航空发动机大修进度管理与控制。本算例运用本文提出的航空发动机大修周期预测方法和传统PERT方法对其进行大修周期预测,比较预测结果后说明了本文所提方法的正确性。 本文针对该型航空发动机大修工艺流程建立了网络计划图,利用Crystal Ball软件进行蒙特卡洛仿真分析。其中,工序时间的概率分布选择往往决定着仿真结果的有效性,本文根据不同的大修工序选择相应的大修时间概率分布,如表1所示。 根据航空发动机大修工艺流程网络图中各工序节点的相互关系绘制形成单代号网络图,如图5所示。图中圆圈中的字母表示大修工序,箭线表示工序之间的逻辑关系。 由文献[14]的方法确定仿真次数,设定β=0.95,查N(0,1)表,得U=1.9;假设ε=3,最终可得n=1 010。 相同条件下对大修周期进行多次仿真运行,并随机抽取10次仿真结果,得出相同完工概率对应下的大修周期预测值,如表2所示。通过方差分析结果表明,每组预测值的变化浮动很小,仿真结果趋于稳定。通过数据拟合可得航空发动机大修周期累积概率密度曲线,如图6所示。根据该曲线,航空发动机大修在580 h可完成总任务的64%,其600 h内完工的概率为84.5%。 表2 完工概率对应下的航空发动机大修周期预测值 续表2 由仿真计算得到该航空发动机大修周期频数统计直方图,如图7所示。从图7可见,航空发动机大修周期分布在495 h~645 h之间,频数最高的集中在570 h附近,随着大修周期的缩短和增长,频数呈现递减趋势。通过拟合,航空发动机大修周期满足β分布,其参数为:期望值为570 h,标准方差为30,α=5.25,β=4.17。 通过仿真可以预测航空发动机大修关键线路的分布情况和大修工序关键度,表3所示为统计得到的大修线路关键概率,表4所示为列出的大修工序关键度,图8所示为该航空发动机大修工序关键度分布,通过该图可以很直观地了解到各大修工序的关键水平。大修线路A-D-M-O-Q-R-T-X出现的频次最高,故为该航空发动机大修的仿真关键线路。关键线路敏感度定义为:次关键线路出现的频数与出现频数最多的关键线路之比。敏感度越小,表明关键线路越稳定。依据这个概念,编号为2的关键线路的敏感度为0.39;编号为3,4的关键线路的敏感度分别为0.07和0.03。表明编号为2的关键线路敏感度较高,而编号为3和4的关键线路稳定,不容易向编号3和4转移。 表3 航空发动机大修线路关键概率统计 表4 航空发动机大修工序关键度 通过比较分析可以发现,本文所提方法预测的航空发动机大修周期延长了20 h,在一定程度上修正了传统PERT方法估算大修周期偏小的问题。另外,实际航空发动机大修过程中受多方面不确定因素的影响,工序的持续时间和工程的控制线路均不确定,因此采用单一的传统PERT方法进行大修进度分析存在很大的局限性。而运用本文方法预测的航空发动机大修关键线路不止一条,从预测结果中可以把握关键线路的转移情况,并且能够得到各工序关键度的分布情况,从而掌握航空发动机大修过程中需要重点关注的大修工序,以便控制航空发动机大修的进度,具有更好的实际大修过程指导作用。 通过对航空发动机大修周期预测结果进行分析,从表3、表4和图7可以得出以下结论,并根据这些结论对实际航空发动机大修进行指导: (1)航空发动机大修过程中,A-D-M-O-Q-R-T-X为该航空发动机大修的仿真关键线路,是影响航空发动机大修周期的关键线路,建议在生产中着重控制;编号为2的关键线路敏感度较高,表明容易向该线路发生转移,生产中也应重点关注该线路。 (2)大修工序中的分解和拆除涡轮盖并移除转子、涡轮转子性能恢复、平衡涡轮转子、修理涡轮转子、修理涡轮盖及试车等大修工序较为关键,在大修过程中需要重点控制。进一步分析可以发现,与转子有关的大修活动的关键度均在0.93以上,表明转子的修理是影响航空发动机大修如期完工的关键,大修过程中应当分配足够的人力物力。 (3)优化关键路线的网络图可以缩短大修周期,例如可以将关键线路中的工序准备、转工环节调整至次要路线,或在关键线路的工序之间设置缓冲时间等。 此外,可以通过更新硬件设施设备、降低设备故障率、实施大修计划网络图管理、优化大修工艺、消除维修差错因素、编制个性化大修工卡、降低大修工序时间不确定性等方法提高大修完工概率,保证航空发动机大修进度。 本文针对不确定条件下航空发动机大修周期预测问题,指出航空发动机大修过程是受多种因素影响的复杂不确定系统,提出一种融合PERT和蒙特卡洛仿真的求解方法。通过分析引起航空发动机大修周期的不确定因素,基于对大修工序逻辑关系的分析,构建符合实际大修过程的大修工序时间概率分布,结合PERT与蒙特卡洛方法,得出航空发动机大修周期的概率分布、关键线路分布及工序关键度。最后以某型航空发动机大修流程为例,验证了所提方法的有效性,使大修生产管理人员可以预先准确把握大修周期、关键线路、工序关键度的变化规律,为航空发动机大修进度控制与工艺优化提供了科学依据。然而,由于影响航空发动机大修周期不确定性的因素众多,且为动态变化,全部识别出对大修周期性影响显著的工艺参数、大修工序以及工艺参数之间的关系会直接影响预测结果的准确性。下一步工作将利用实际生产数据,依据预测结果与实际生产进行对比分析,进一步改进优化预测模型,同时结合全局综合敏感性分析方法对大修周期的不确定性展开更深入的研究,以进一步提高预测结果的准确性。 [1] ZHANG Xuebin, CHEN Yunxiang, WANG Chao, et al. Method on military aircraft engine overhaul capacity evaluation[J]. Fire Control & Command Control,2016,41(1):37-40(in Chinese).[张学斌,陈云翔,王 超,等.军用航空发动机大修能力评估方法[J].火力与指挥控制,2016,41(1):37-40.] [2] YU Fen, YU Yilin, ZHU Shixing, et al. Research on process optimization of B747 overhaul[J].Manufactring Automation,2012,34(14):32-35(in Chinese).[余 芬,喻益琳,祝世兴,等.B747飞机大修作业流程优化研究[J].制造业自动化,2012,34(14):32-35.] [3] MA Xiaole, MA Tao, WANG Hong. Simulation analysis on aircraft overhaul based on network plan technology[J]. Journal of Naval Aeronautical and Astronautical University,2016,15(1):83-88(in Chinese).[马晓乐,马 涛,王 宏.基于网络图的飞机大修进度模拟分析[J].海军航空工程学院学报,2016,15(1):83-88.] [4] ATLI O, KAHRAMAN C. Aircraft maintenance planning using fuzzy critical path analysis[J].International Journal of Computational Intelligence Systems,2012,5(3):553-567. [5] LI Chengchuan, LI Congbo. Uncertain remanufacturing proc-ess routings model for used components based on GERT network[J]. Computer Integrated Manufacturing Systems,2012,18(2):298-305(in Chinese).[李成川,李聪波.基于GERT图的废旧零部件不确定性再制造工艺路线模型[J].计算机集成制造系统,2012,18(2):298-305.] [6] YANG Ming, LI Yuan, ZHANG Kaifu, et al. Approach bas-ed on improved-PERT for better risk evaluation of aviation project[J]. Computer Integrated Manufacturing Systems,2008,14(1):192-196(in Chinese).[杨 铭,李 原,张开富,等.基于改进的计划评审技术的航空项目风险评价技术研究[J].计算机集成制造系统,2008,14(1):192-196.] [7] LI Xiaolong, PAN Guoqiang, WU Wenguang. Simple study on the overhaul’s characteristic which is based on the overhaul process and contrast with production[J]. Equipment Manufactring Technology,2011,10(8):144-145(in Chinese).[李小龙,潘国强,武文光.基于装备大修过程的大修与生产特点对比浅析[J].装备制造技术,2011,10(8):144-145.] [8] XU Hang, ZHU Yifan, CHEN Chunliang. Simple study on the overhaul’s characteristic which is based on the overhaul process and contrast with production[J]. Journal of System Simulation,2006,18(10):2945-2947(in Chinese).[徐 航,朱一凡,陈春良.战伤装甲装备修理工时仿真及其分布规律研究[J].系统仿真学报,2006,18(10):2945-2947.] [9] TANG Xinmin. Aero-engine workshop maintenance procedure modeling based on Petri-nets and its application[D]. Harbin:Harbin Institute of Technology,2007(in Chinese).[汤新民.基于Petri网的航空发动机车间维修过程建模及其应用研究[D].哈尔滨:哈尔滨工业大学,2007.] [10] LI Congbo, LI Lingling, CAO Huajun, et al. Fuzzy learning system for uncertain remanufacturing process time of used components[J]. Journal of Mechanical Engineering,2013,49(15):137-146(in Chinese).[李聪波,李玲玲,曹华军,等.废旧零部件不确定性再制造工艺时间的模糊学习系统[J].机械工程学报,2013,49(15):137-146.] [11] ZHU Haiping, ZHAO Yu, WU Jun, et al. Application of neural network ensemble in prediction of product due date[J]. Computer Integrated Manufacturing Systems,2007,13(11):2140-2144(in Chinese).[朱海平,赵 玉,吴 军,等.神经网络集成方法在产品完工期预测中的应用[J].计算机集成制造系统,2007,13(11):2140-2144.] [12] LI Ming, YAO Li, YANG Jin, et al. Due date assignment and dynamic scheduling of one-of-a-kind assembly production with uncertain processing time[J]. International Journal of Computer Integrated Manufacturing,2015,28(6):616-627. [13] WANG Liming, SHI Fenglong, ZHU Huayuan, et al. Equipment support program evaluation based on Monte Carlo method[J]. Ordnance Industry Automation,2016,35(1):23-27(in Chinese).[王利明,史凤隆,祝华远,等.基于蒙特卡罗法的装备保障方案评估[J].兵工自动化,2016,35(1):23-27.] [14] ZHONG Denghua, LIU Kuijian, YANG Xiaogang. Uncertainty analysis for construction scheduling with flexible network sinmlation[J]. Systems Engineering—Theory & Practice,2005,25(2):107-112(in Chinese).[钟登华,刘奎建,杨晓刚.施工进度计划柔性网络仿真的不确定性研究[J].系统工程理论与实践,2005,25(2):107-112.] [15] REMÉNYI C, STAUDACHER S. Systematic simulation based approach for the identification and implementation of a scheduling rule in the aircraft engine maintenance[J]. International Journal of Production Economics,2014,147(5):94-107. [16] SU Chun, CAO Baixue. Dynamic bottleneck analysis for remanufacturing system considering quality uncertainty[J].Computer Integrated Manufacturing Systems,2014,20(5):1062-1069(in Chinese).[苏 春,曹白雪.考虑质量不确定性的再制造系统动态瓶颈分析[J].计算机集成制造系统,2014,20(5):1062-1069.] [17] SUN Lu. Research on schedule management of aerospace project[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012(in Chiense).[孙 璐.航天型号研制项目进度计划管理研究[D].南京:南京航空航天大学,2012.] [18] ELMAGHRABY S E. On criticality and sensitivity in activity networks[J]. European Journal of Operational Research,2000,127(2):220-238. [19] LIU Kuijian. Real-time control for construction scheduling of large scale underground structure group[D].Tianjin:Tianjin University,2007(in Chinese).[刘奎建.大型地下洞室群施工进度实时控制研究[D].天津:天津大学,2007.] [20] SUN Erman, XU Cheng. Monte Carlo simulation and analysis of equipment development schedule’s critical path[J]. Ordnance Industry Automation,2016,35(1):15-19(in Chinese).[孙尔蔓,许 诚.装备研制进度关键路径的Monte Carlo模拟与分析[J].兵工自动化,2016,35(1):15-19.]3.2 工序时间概率分布及抽样公式
4 算例分析
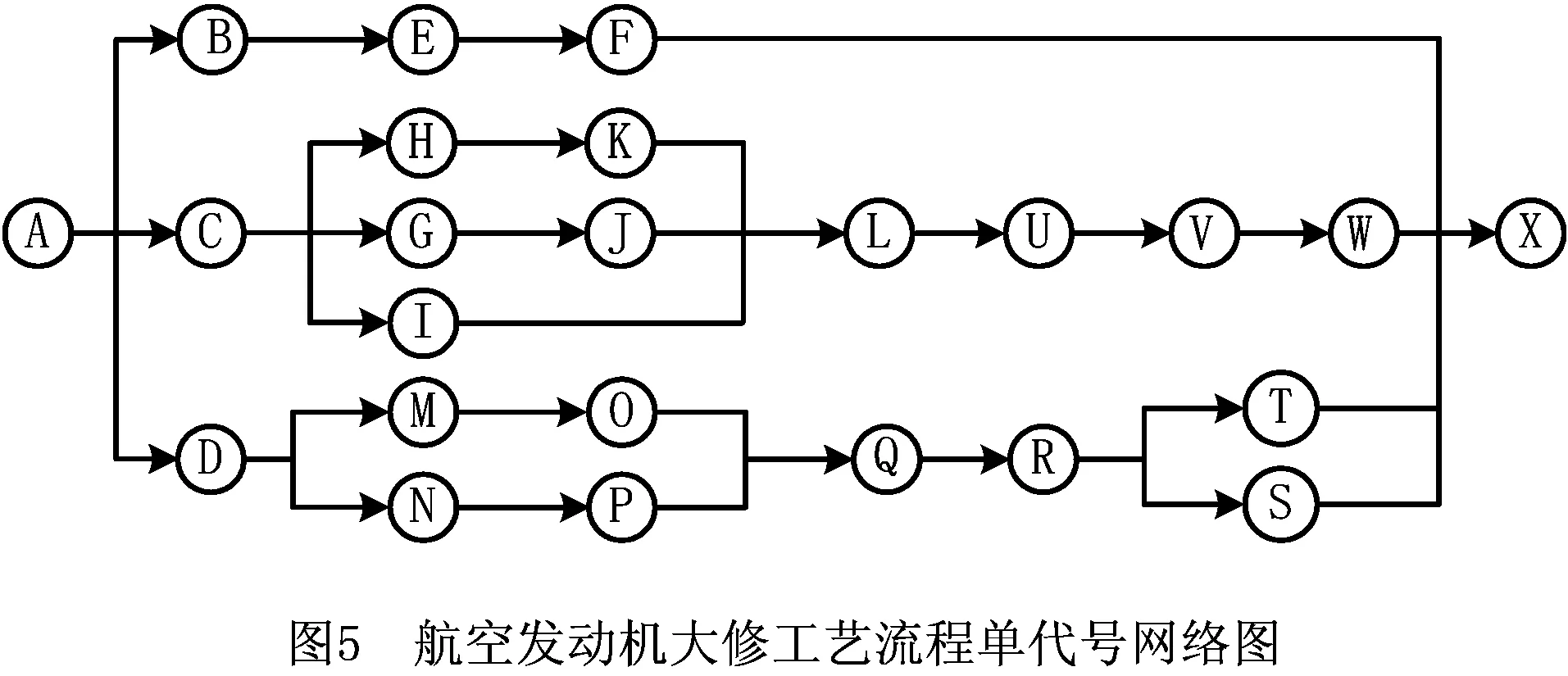
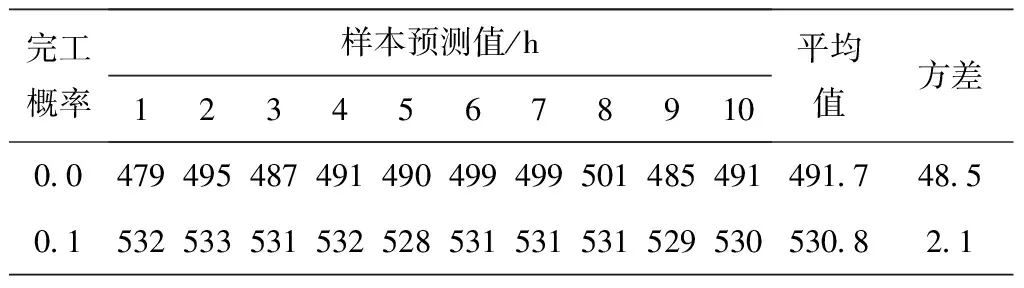


5 结束语
