基于混合模型与流形调节的晶圆表面缺陷识别

卢笑蕾，余建波

(同济大学 机械与能源工程学院，上海 200000)

0 引言

半导体制造是一个复杂且耗资巨大的过程。在制造过程中，由于工艺的繁杂与动态性，半导体晶圆表面容易出现缺陷。通常,晶圆表面的缺陷分为全局缺陷和局部缺陷两类[1]，全局缺陷常因一些随机因素导致(如灰尘)，分布于整个晶圆的表面，而局部缺陷一般由可寻原因导致，如人为因素、设备故障等。局部缺陷一般以各种簇的形式存在，常见的有线形、曲线形和椭球形。对于工程师而言，缺陷簇的位置、大小和几何形状等都可以反映生产过程中的问题[2]，例如晶圆与设备之间摩擦产生刮痕，容易导致线形缺陷，因此准确识别局部缺陷簇的形状，不仅可以避免因大批量晶圆缺陷而造成的成本损失，更重要的是可以根据缺陷原因找出生产线上存在的故障源，从而进行调整与改进，减少晶圆生产中的返工率和废品率，提高晶圆质量和生产效率。

传统的缺陷检测往往通过电子扫描显微镜完成，因为生产数量庞大，这种人工检测已经不能解决实际问题[2]，所以越来越多的研究开始集中在缺陷自动检测领域。Friedman等[3]采用奈A型分布(Neyman type-A distribution)拟合晶圆表面的缺陷，Cunningham等[4]基于晶圆缺陷点的空间位置、形状等展开量化分析。这些研究仅集中于晶圆缺陷模式的统计分析，很难进一步识别出缺陷模式的具体形状。Su等[5]研究了一套有监督神经网络系统用于晶圆缺陷检测，包括反向传播、径向基函数和学习矢量量化;Chen等[6]采用无监督神经网络，即采用自适应共振理论(Adaptive Resonance Theory, ART)识别晶圆表面缺陷。同时也有很多学者利用有监督机器学习，通过收集先验数据建立训练库，从而对线上采集的缺陷模式进行分类识别，如K最近邻[7](K-Nearest Neighbor, KNN)、C4.5决策树[7]、支持向量机[8](Support Vector Machine, SVM)。在晶圆表面缺陷检测中，这些方法都有一定的效果，但仍存在很多不足[2]，例如基于监督/无监督的方法不能检测出一个晶圆表面存在的多种缺陷模式，而且对于决策函数的参数估计通常需要大量的训练样本，计算量庞大，非常耗时。

近年来，越来越多的学者集中研究可直接识别晶圆表面缺陷的基于模型聚类的方法。与上述方法相比，基于模型聚类的缺陷检测有两个突出的优势[9]：①不需要训练数据，可直接在线检测晶圆表面缺陷，而且可以很好地应对线上出现的新缺陷模式；②基于模型聚类的结果，在检测出晶圆表面缺陷的同时也能够识别缺陷模式。在基于模型聚类的方法中，晶圆表面的所有晶粒服从混合分布，其中一个缺陷簇中的点属于相同分布模型，如多元正态分布。Hwang等[10]提出两步聚类法：①采用二元正态分布对晶圆表面所有缺陷簇进行聚类，并采用贝叶斯信息准则确定簇的数目；②采用主曲线对所有缺陷簇进行聚类。通过比较两种模型中每个簇的似然概率值，判定该簇是否为曲线形。虽然两步聚类法在晶圆缺陷检测上取得了很好的应用，但是当晶圆表面存在曲线形缺陷模式时，这套算法容易过多地估计缺陷簇的数目，因为它假设晶圆表面所有缺陷服从二元正态分布。Yuan等[9]对两步聚类法进行改进，加入了主曲线模型，可以同时对曲线形、线形和椭球形进行建模，并提出分类期望最大化(Classification Expectation Maximization，CEM)算法估计模型参数。Yuan提出的模型在仿真案例中具有一定的适用性，但在实际生产中面对大量的晶圆，其缺陷检测十分耗时。

本文提出一套基于混合学习模型和流形调节的晶圆表面缺陷检测与识别系统，旨在检测晶圆表面缺陷的同时准确地判断缺陷簇的个数和识别缺陷簇的形状。该系统首先利用层次聚类的方法将晶圆表面的局部缺陷划分为缺陷簇，并提出一种基于轮廓系数(silhouette coefficient)[11]的标准确定最优缺陷簇个数，准确判定晶圆表面存在的缺陷簇数目。针对晶圆表面缺陷模式的分布情况，该系统充分考虑数据在空间子流形上的分布，采用基于流形调节的局部连续高斯模型[12](Gaussian Mixture Model with Local Consistency, LCGMM)，很好地描述了晶圆表面线形、椭球形缺陷簇的分布，同时针对曲线形缺陷模式，加入主曲线模型[13](Principal Curve, PC)，实现了对晶圆表面几种常见缺陷模式的统计描述建模。在完成初始建模识别的基础上，本文提出集成LCGMM和PC的混合模型，并采用CEM(classification-expectation-maximization)算法[1]估计混合模型参数。本文提出的晶圆表面缺陷检测与识别系统的最主要贡献在于：①提出一种基于轮廓系数[11]的缺陷簇个数选择指标，可以有效判断晶圆表面缺陷簇的个数；②构建基于LCGMM和PC的混合模型，提高了晶圆表面缺陷识别的准确性。在仿真案例和实际案例上的实验结果表明，本文提出的晶圆表面缺陷检测与识别系统具有很好的适用性。

1 晶圆缺陷检测与识别系统

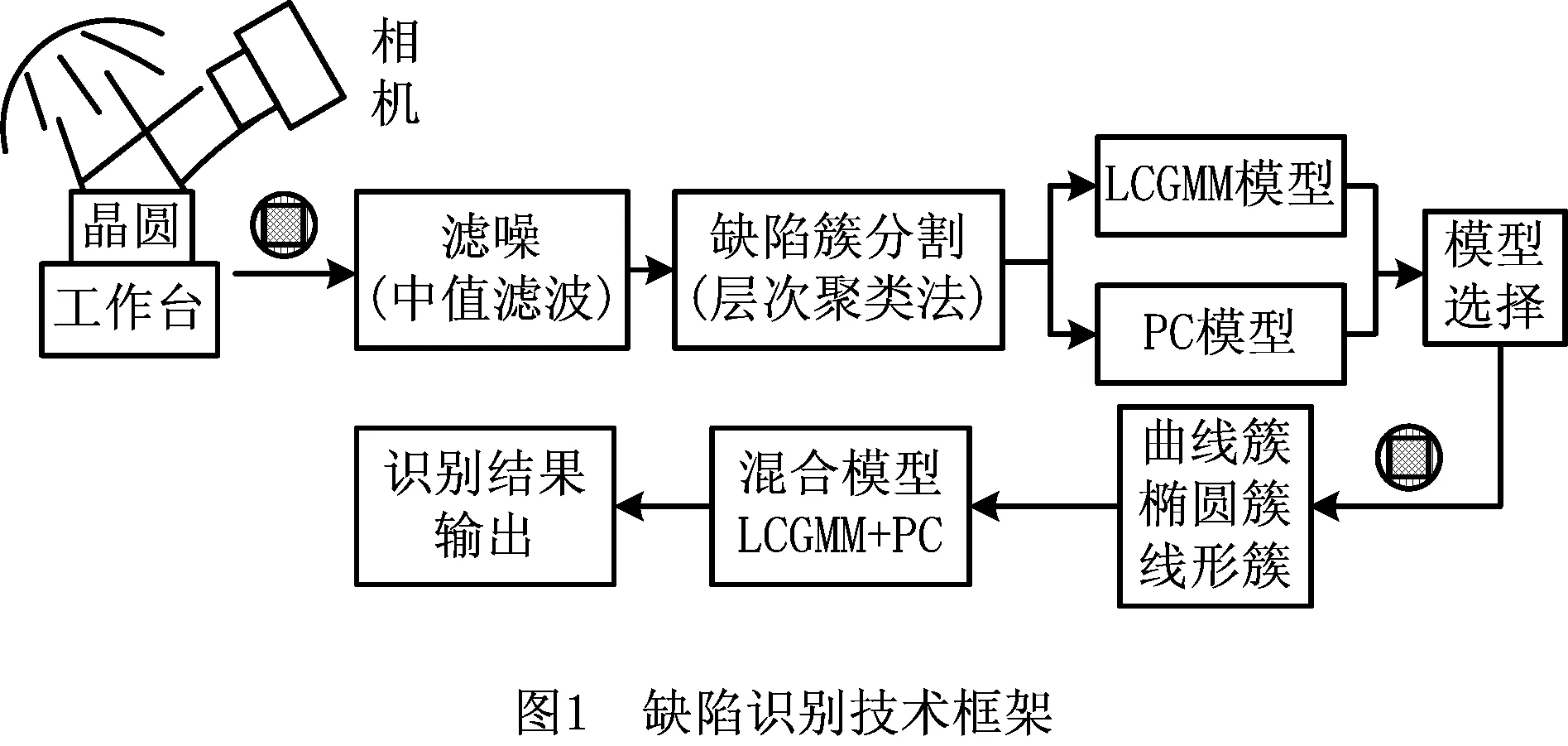
本文提出的晶圆表面缺陷检测和识别系统方案如图1所示。由于半导体制造过程中多源随机因素的影响，晶圆图通常混杂各种噪声，系统首先采用中值滤波技术对晶圆图进行滤噪处理，有效保留晶圆表面的局部缺陷，提高系统检测与识别的性能。晶圆表面的局部缺陷通常以簇的形式存在，为了准确划分缺陷簇并判定其数目，该系统使用层次聚类法有效地分离晶圆表面的缺陷簇，并采用轮廓系数指标[12]选择最优簇数目。在缺陷簇形状识别中，本文在高斯混合模型(Gaussian Mixture Model, GMM)的基础上引入流形调节，采用LCGMM，并加入PC模型，将缺陷识别转化为模型选择的问题。由于初始聚类仅依赖晶粒之间的距离，在完成初始建模识别的基础上，系统通过融合LCGMM和主曲线模型构建混合模型,对晶圆表面缺陷重新建模识别，来提高缺陷簇划分和识别的准确性。

1.1 缺陷聚类

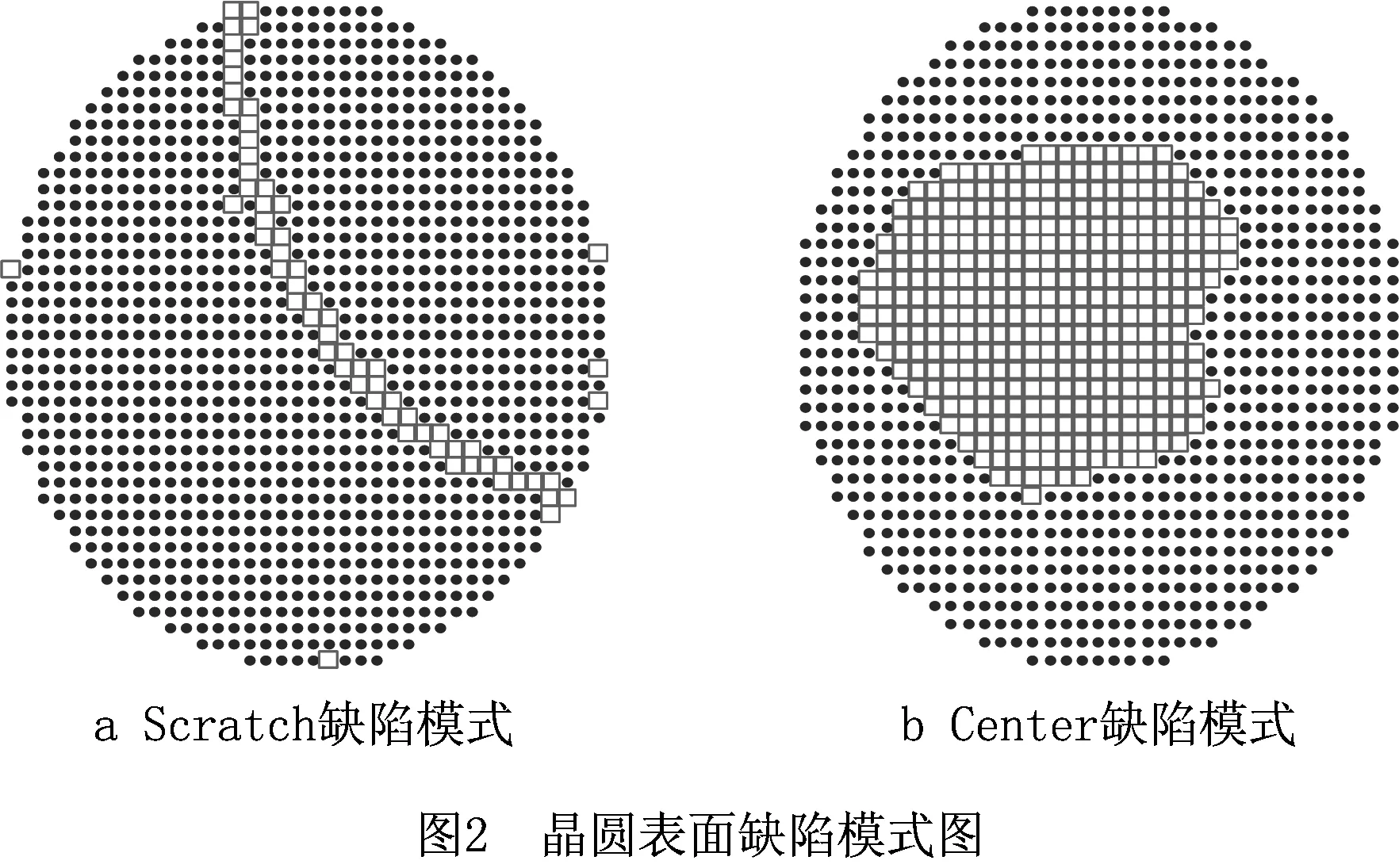
半导体晶圆表面的局部缺陷通常以簇的形式存在，准确划分缺陷簇对识别缺陷模式具有重要意义，图2所示为晶圆表面常见的两种缺陷形状(曲线形和椭球形)。本文选取层次聚类法划分晶圆表面的缺陷簇。层次聚类法是根据给定的簇间距离度量准则，构造和维护一棵由簇和子簇形成的聚类树，直至满足某个终结条件为止。一般有两种类型的层次聚类方法[11]：①凝聚层次聚类，将每个对象作为一个簇，合并这些簇直至所有的对象都在一个簇中；②分裂层次聚类，将所有对象置于一个簇中，逐步细分为越来越小的簇，直至每个对象自成一簇。对于任意两个簇之间的距离度量，常用的有最小距离(single-link)、最大距离(complete-link)、平均距离(average-link)和最小方差法(ward-link)等。图3所示为利用4种距离度量方法对一个晶圆表面所有缺陷点聚类的情况。

晶圆表面通常同时存在几种缺陷模式，利用层次聚类法完成划分时，如果判定缺陷簇个数不准确，则将直接影响后面的缺陷识别。为了确定晶圆表面缺陷簇的个数，本文采用轮廓系数[11]指标进行判断。轮廓系数结合每个样本与自身所在簇的分离度和与其他簇的凝聚度，其值越大，聚类效果越好。事先确定多个簇数目，通过计算每个簇个数条件下的轮廓系数，选取轮廓系数最大所对应的簇个数为最优值。图4所示为4种晶圆缺陷模式(如图5)下的聚类簇数目判别情况，所有模式均在K=2时取得最大值，说明每种模式中含有两个缺陷簇，判定结果正确。

1.2 缺陷识别

晶圆表面缺陷簇常见的有线形、曲线形和椭球形，每种形状均可反映半导体生产过程中存在的问题，例如晶圆与设备之间摩擦产生的刮痕容易导致线形缺陷，因此准确识别晶圆表面缺陷簇的形状，可辅助识别与调整生产线上的故障源。本文将缺陷识别分为两步进行：①应用LCGMM和PC模型，针对不同的缺陷簇选用不同的模型分别建模，将缺陷模式的识别视为模型选择的过程；②初始建模识别完成后，晶圆表面缺陷簇的个数和形状已知，通过融合LCGMM和PC模型构建一个混合模型，对晶圆表面缺陷簇进行识别来提高识别的准确性。

下面详细介绍LCGMM、PC模型和混合模型的各自建模过程。

1.2.1 局部连续高斯混合模型

针对晶圆表面线形、椭球形缺陷模式，一般采用高斯混合模型[9]对其进行建模。通常晶圆表面缺陷数据的自由度比实际维度低很多[14]，高斯混合模型并没有考虑缺陷数据分布在环绕空间的子流形上，因此在拟合线形、椭球形这些缺陷模式时，高斯混合模型很容易出现过拟合现象[12]。本文采用Liu提出的LCGMM，通过对高斯混合模型的似然函数引入正则化，充分考虑缺陷数据边缘分布的内部几何信息，从而准确地拟合缺陷簇分布。高斯混合模型可以很好地对椭圆簇或线形簇[15]进行建模，一个d维多元正态分布(Multivariate Normal Distribution，MVN)为

(1)

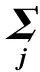
高斯混合模型可以看作不同高斯分布的线性叠加，即

(2)

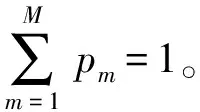
由于观测值中的样本各自属于第几个高斯分布未知，即p(c|x)为隐变量(c表示第c个高斯分布)，一般通过EM(expectation-maxmization)算法[15]对模型进行参数估计，E步计算p(c|x)的期望值，M步通过最大化完全似然概率求取参数，不断迭代直至满足收敛条件。对于一组观测变量X=(x1,x2,…,xN)，模型的不完全似然概率函数如式(3)所示，完全似然概率函数如式(4)所示。

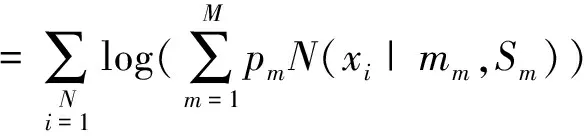
(3)

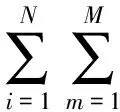
logN(xi|mm,Sm))。

(4)

LCGMM通过对似然函数(3)引入正则化，充分考虑了数据边缘分布的内部几何信息。首先构建近邻图描述非线性流形结构[16]，边缘权重矩阵

(5)

式中Np(xi)表示xi的p最近邻。

通过KL散度(KL-divergence)衡量两种分布Pi(c)和Pj(c)之间的相似度，即

(6)

为了保证对称，可写作

(7)

令Pi(c)=P(c|xi)，根据上述近邻图的权重矩阵，通过式(8)描述近邻图中P(c|x)的平滑度：

Pj(c))+D(Pj(c)‖Pi(c)))Wij。

(8)

式中R越小，P(c|x)在图中越平滑。通过整合R和GMM的似然概率函数，得出目标函数如下：

总体来说，在水利工程的施工建设过程中，导致出现堤坝渗漏问题的直接因素与间接因素很多，虽然长期以来这些问题一直存在，但却需要我们慎重对待，不仅要对防渗漏问题予以高度的重视，而且还应加大力度改进加固技术。在施工过程中，还要注重结合工程具体情况，使其既能制定出具有针对性的解决方案，同时还能确保方案的有效落实与执行，务必在保证施工质量得以全面优化控制下，使水利工程堤坝防渗加固工作得以切实有效地开展。

=L-λR

(D(Pi(c)‖Pj(c))+D(Pj(c)‖Pi(c))))Wij。

(9)

式中:Pi(c)为P(c|xi)的缩写，λ为正则化系数。可通过EM算法对目标函数进行参数估计。

1.2.2 主曲线模型

对于曲线形缺陷簇，LCGMM不能很好地描述其特性，而PC可以有效地对曲线的缺陷模式进行建模。Standford等[17]假设曲线上的特征点服从正态分布，均值为0，方差为sj，PC的概率密度函数为

(10)

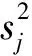
1.2.3 基于LCGMM和PC的混合学习模型

本文设计的系统利用层次聚类法划分晶圆表面的局部缺陷簇，由于初始聚类仅依赖晶粒之间的距离，对缺陷簇边界的晶粒很容易出现误分的情况，从而影响后续的缺陷模式识别。本文在完成初始聚类识别后，构建基于LCGMM和PC的混合模型，该模型可对晶圆表面的缺陷簇进行建模识别，修正缺陷簇边界晶粒误分情况，提高缺陷模式识别的准确性。混合模型的目标函数为

(11)

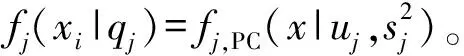
(1)求期望

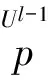
(13)

i=1,…,n,j=0,…,N。

(14)

(2)分类

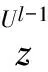
(3)最大化

(15)

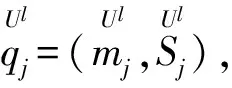
(16)

(17)

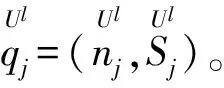
不断重复步骤1)～3)，直至满足收敛条件

(18)

2 实验与结果分析

为了验证本文提出的晶圆表面缺陷检测与识别系统的有效性，分别通过仿真案例和工业案例进行实验分析。在仿真案例中，通过事先确定的缺陷簇形状，根据聚类和识别的准确性测试系统的性能，工业案例中则选取几种常见的晶圆缺陷模式测试系统的性能。

2.1 仿真案例分析

首先采用仿真缺陷模式验证所提方法的有效性。实验中，仿真产生曲线形、椭圆形、圆形3种常见的缺陷模式，并通过组合的方式使其呈现在晶圆表面，例如图5a和图5b为分离模式，图5c为交叉模式，图5d为邻接模式。椭圆形和圆形均通过对二元正态分布随机采样获得，曲线形是截取圆形的一段。图6所示为利用层次聚类法进行晶圆表面缺陷聚类的结果。

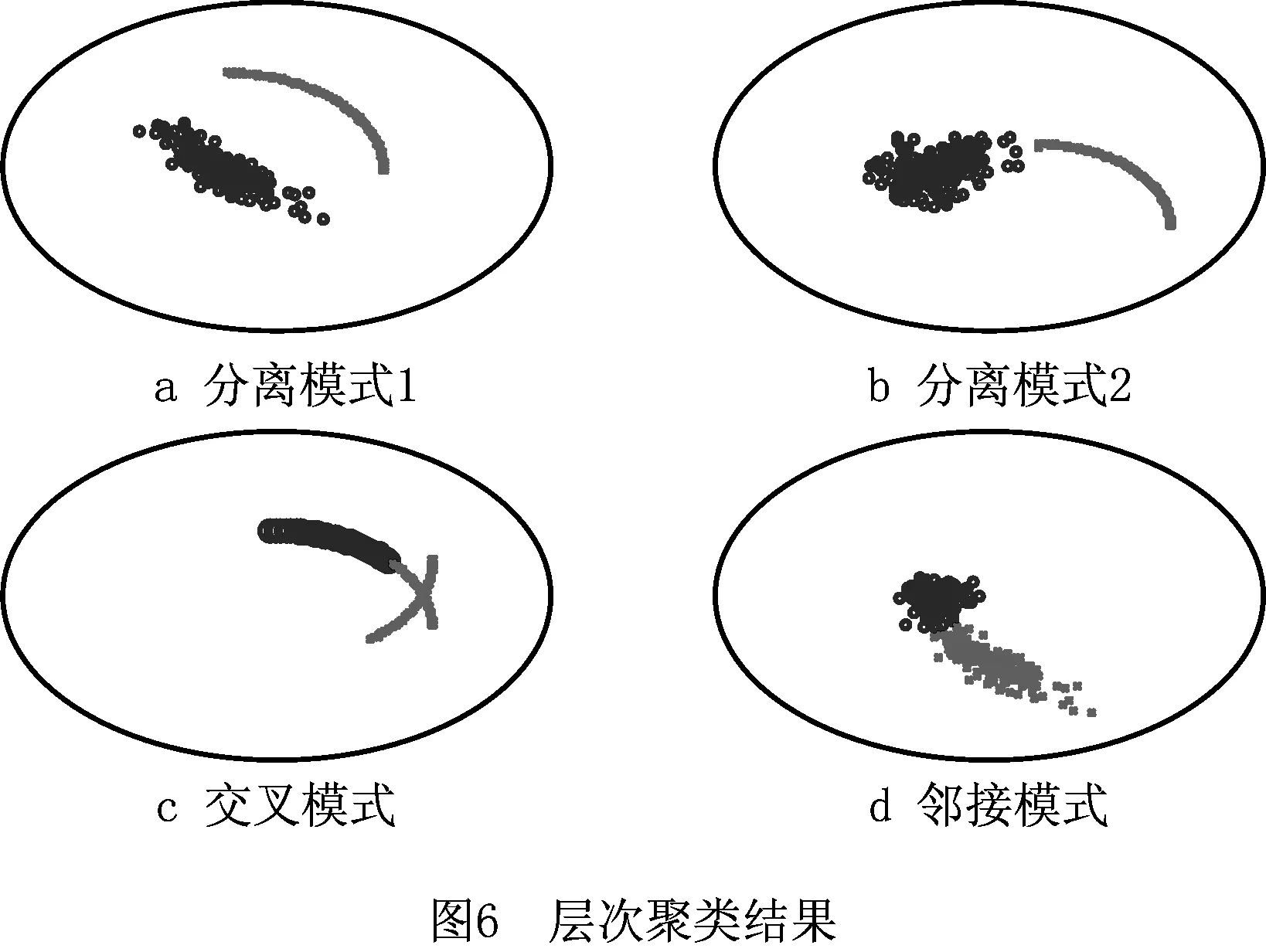
为了测试层次聚类法和基于LCGMM与PC的混合模型聚类法的性能，本文选取典型的K-means和模糊C聚类[18]进行对比，因为这两种方法已应用于晶圆表面缺陷识别[19]。K-means对大规模数据进行聚类时效率较高，属于基于划分的聚类方法，该方法通过初试随机划分K个簇，采用平方误差准则不断重复迭代直至其最小；不同于K-means为代表的硬聚类方法，模糊C聚类采用隶属度确定每个数据点属于某个簇的程度，通过构建隶属矩阵实现模糊C划分。表1所示为几种方法的聚类性能，可以看出，这几种聚类方法都可以很好地区分分离模式1和模式2，但是混合模型在识别交叉模式和分离模式时显著好于其他方法，该结果进一步证明了所提方法的有效性。

表1 晶圆缺陷识别率 %

注：抓取率=正确分类缺陷数/总缺陷数。

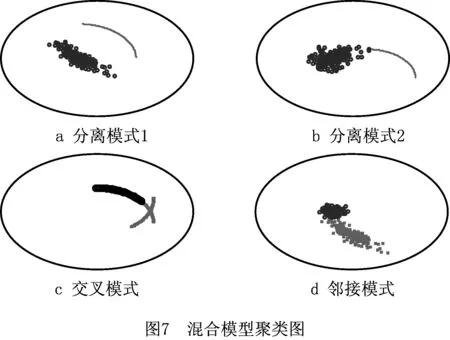
当系统完成晶圆表面缺陷簇的分割后，便通过LCGMM模型和PC模型分别对每个缺陷簇进行建模识别。表2所示为各个簇在每种模型中的似然概率值，PC模型和LCGMM模型能够很好地区分曲线形和椭圆形。例如图5a中，对于曲线形，PC的似然概率值大于LCGMM的似然概率值，而椭圆形则相反。LCGMM模型识别出的簇，可根据协方差的特征值进一步判别簇的形状，例如图6d中，空心圆簇的特征值之比为0.75，接近1，可判定为圆形；圆心簇的特征值之比为0.103 2，远小于1，则判定为椭圆。当晶圆表面缺陷簇的个数和形状已知时，通过构建混合模型重新对缺陷簇进行建模识别，结果如图7所示。表1同时列出了基于混合模型的缺陷簇划分正确率，例如图6c中，交叉模式的准确率提升了4.32%，邻接模式的准确率也提了2.25%，可以看出通过混合模型重新建模识别的方法显著提高了晶圆表面缺陷簇划分的准确性。

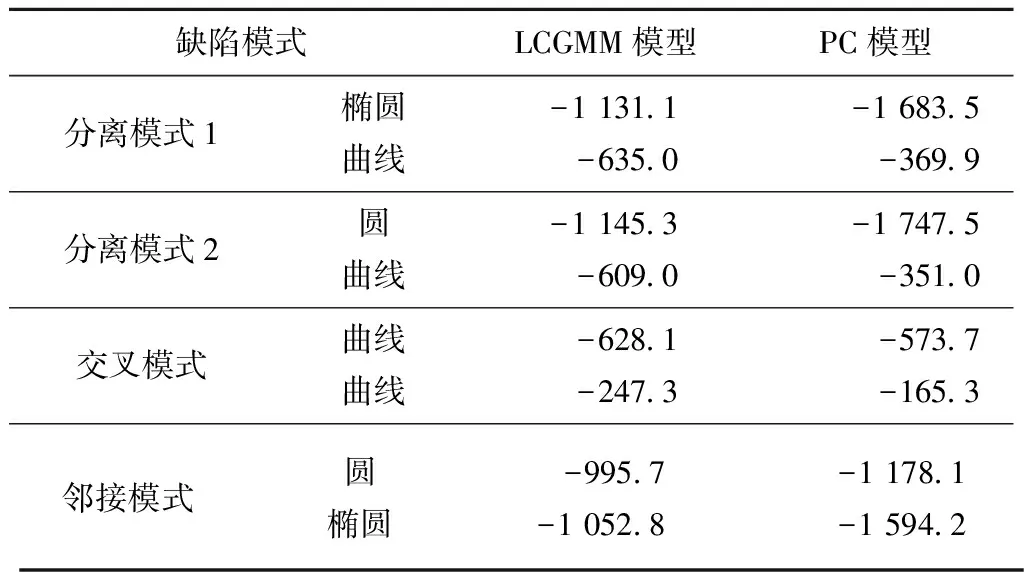
表2 晶圆缺陷模式建模比较

2.2 工业案例分析

本文采用实际半导体制造过程中采集的晶圆图像数据(称为WM-811K数据)验证所提晶圆缺陷探测与识别方法的有效性。该数据集为工业现场采集的晶圆数据，包括811 457张晶圆图，所有晶圆图数据都已通过专家分析标定其缺陷模式，有关WM-811K数据更多的信息及数据获取方式可参考文献[20]。本文从WM-811K数据集中选取两种缺陷模式(Center和Scratch)，各取两个样本进行分析。图8和图9所示分别为两种晶圆缺陷模式的滤噪和聚类结果。完成聚类后，在识别过程中，LCGMM模型能够识别出Center模式，其中两个缺陷晶圆的特征值之比分别为0.765 4和0.768 0，接近1，可识别为圆形，即Center缺陷。对于图8中的Scratch模式，PC模型能够很好地识别出曲线形。

3 结束语

本文提出一套基于混合学习模型与流形调节的晶圆缺陷检测与模式识别系统，该系统使用轮廓系数准确判断晶圆表面的缺陷簇个数。然后提出基于LCGMM和PC模型的混合模型，实现了对晶圆表面局部缺陷模式分布的统计描述建模，从而可以有效识别晶圆表面缺陷簇的形状，如常见的线形、曲线形和椭球形缺陷模式。在仿真案例中，本文设计的系统在抓取率和形状识别的准确性上都取得了很好的结果，而且在实际案例的测试中也能够很好地识别出晶圆表面的各种缺陷模式。线上实时识别晶圆缺陷模式将加速确定缺陷产生的故障源，减少晶圆生产中的返工率和废品率，显著提高晶圆质量和生产效率。

后续工作将集中研究晶圆表面缺陷簇更多形状的统计建模，并应用到实际晶圆生产过程中的缺陷模式探测与识别。

[1] YUAN T, KUO W, BAE S J.Detection of spatial defect patterns generated in semiconductor fabrication processes[J].IEEE Transactions on Semiconductor Manufacturing，2011，24(3):392-403.

[2] WANG C H, KUO W, BENSMAIL H. Detection and classification of defect patterns on semiconductor wafers[J]. IIE Transactions,2006,38(12):1059-1068.

[3] FRIEDMAN D J, ALBIN S L. Clustered defects in IC fabrication:impact on process control charts[J]. IEEE Transactions on Semiconductor Manufacturing，1991，4(1):36-42.

[4] CUNNINGHAM S P, MACKINNON S. Statistical methods for visual defect metrology[J]. IEEE Transactions on Semiconductor Manufacturing，1998，11(1):48-53.

[5] SU C T, YANG T, KE C M. A neural-network approach for semiconductor wafer post-sawing inspection[J].IEEE Transactions on Semiconductor Manufacturing，2002，15(2):260-266.

[6] CHEN Feilong, LIU Shufan. A neural-network approach to recognize defect spatial pattern in semiconductor fabrication[J]. IEEE Transactions on Semiconductor Manufacturing,2000,13(3):366-373.

[7] DASARATHY B V. Nearest neighbor(NN)norms:NN pattern classification techniques[M]. Washington,D.C.,USA:IEEE Computer Society Press,1991.

[8] BALY R, HAJJ H. Wafer classification using support vector machines[J].IEEE Transactions on Semiconductor Manufacturing，2012,25(3):373-383.

[9] YUAN T, KUO W.A model-based clustering approach to the recognition of the spatial defect patterns produced during semiconductor fabrication[J].IIE Transactions,2007,40(2):93-101.

[10] HWANG J Y, KUO W.Model-based clustering for integrated circuit yield enhancement[J].European Journal of Operational Research,2007,178(1):143-153.

[11] ROUSSEEUW P J. Silhouettes:a graphical aid to the interpretation and validation of cluster analysis[J]. Journal of Computational and Applied Mathematics,1987,20(1):53-65.

[12] LIU Jialu, CAI Deng, HE Xiaofei. Gaussian mixture model with local consistency[C]//Proceedings of the 24th AAAI Conference on Artificial Intelligence . Menlo Park, Cal., USA:AAAI,2010:512-517.

[13] STANFORD D C, RAFTERY A E. Finding curvilinear features in spatial point patterns:principal curve clustering with noise[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2000,22(6):601-609.

[14] TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science,2000,290(5500):2319-2323.

[15] BANFIELD J D, RAFTERY A E. Model-based Gaussian and non-Gaussian clustering[J]. Biometrics,1993,49(3):803-821.

[16] DEMPSTER A P, LLIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society, Series B,1977,39(1):1-38.

[17] STANFORD D C, RAFTERY A E.Finding curvilinear features in spatial point patterns:principal curve clustering with noise[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(6):601-609.

[18] LI Jie，WANG Yunfeng，ZHU Zhaoxian，et al.Research on manufacture cell construction method based on fuzzy technology[J].Computer Integrated Manufacturing Systems，2004,10(12):1561-1566m(in Chinese).[李 杰,王云峰，朱昭贤，等.基于模糊技术的制造单元构建方法研究[J].计算机集成制造系统，2004，10(12):1561-1566.]

[19] WANG C H.Recognition of semiconductor defect patterns using spatial filtering and spectral clustering[J].Expert Systems with Applications,2008,34(3):1914-1923.

[20] WU Mingju, JANG J S R,CHEN J L.Wafer map failure pattern recognition and similarity ranking for large-scale data sets[J].IEEE Transactions on Semiconductor Manufacturing,2015,28(1):1-12.