基于RBF神经网络的航空叶片铣削残余应力预测

周金华，任军学，蔡 菊

(西北工业大学 机电学院 现代设计与集成制造技术教育部重点实验室，陕西 西安 710072)

0 引言

铣削残余应力对航空发动机薄壁叶片的表面完整性、加工精度和尺寸稳定性等有重要影响。作为航空发动机的热端部件，高温合金叶片常工作在高速、高温及高压的环境中，其失效形式往往表现为疲劳破坏。高温合金GH4169精密铣削后的残余应力一般表现为拉伸应力，而残余拉应力会促进裂纹萌生，加速裂纹扩展，进而降低航空叶片的疲劳寿命。因此，工程实践中往往希望获得压缩的残余应力，以提高叶片的疲劳寿命。

影响残余应力的因素十分复杂，包括工件的材料属性[1-2]、刀具几何结构[1-3]、切削参数[1,3-5]、走刀路径/顺序和冷却条件[1]等，因为切削残余应力对工艺参数十分敏感，它们之间的映射关系难以依靠经验函数再现，所以切削残余应力的预测十分困难。目前对切削残余应力的研究主要从基于弹塑性力学的解析法、有限元法(Finite Element Method, FEM)和实验测试3个方面展开。自Liang等[6]和Ulutan等[7]于2007年提出正交切削残余应力的解析建模方法后，解析法被扩展至更加复杂的切削工况，铣削方面仅限于相对简单的端铣刀[8]。由于刀具—工件接触关系复杂、接触应力难以计算，球头刀的铣削残余应力理论预测目前难以实现，解析法一般采用Hertz接触模型计算刀具—工件接触应力，部分地将弹性理论应用于塑性变形过程会引起一定偏差。FEM模拟切削残余应力的困难之一是耗时过长，尤其是三维复杂切削，当切削力/温度有限元仿真时，需要对刀尖邻域的刀具与工件材料进行网格细化，刀具划过后再将这部分网格稀疏化，然而进行切削残余应力仿真时，细化的网格不能再被稀疏化，因此网格规模十分庞大，计算效率较低[9]。为提高仿真效率，Valiorgue[10]避开切屑形成的仿真，将等效的热—力载荷直接施加于工件表面，完成正交切削残余应力的仿真，随后将该方法发展至车削残余应力的预报[11-12]，因为该方法并不仿真切屑的形成，所以极大地提高了仿真效率，但由于进行了大量简化，其预测精度还有待进一步验证。然而，无论采用解析方法还是FEM都是对真实切削过程的逼近，需对切削过程进行简化，例如二者均未考虑相变因素，因此预测精度仍然是一个普遍存在的问题。

实验手段不存在相变问题，是当前切削残余应力的主要研究手段之一，其中X射线法测试残余应力由于不具破坏性而被广泛应用。基于实验样本对切削残余应力进行预测的方法主要有响应曲面法(Response Surface Model, RSM)、经验模型和BP(back propagation)神经网络等[13]。Fuh等[3]应用RSM方法对铝合金2014-T6的端铣残余应力进行了预测；Saini等[14]基于BBD(Box-Behnken design)实验设计，建立了AISI H11工具钢硬态车削残余应力的响应曲面模型，并研究了切削速度、进给量、切削深度及刀尖半径对残余应力的影响;Axir[15]针对5种不同的材料建立了残余应力沿深度分布的预测模型，该模型假定残余应力分布为深度的函数，进而采用RSM建立分布函数系数与材料强度、切削速度和进给率之间的映射关系，然而该模型有过多的待定系数，并没有得到广泛应用;Zhang等[1]将BP神经网络应用于硬态车削，建立了一个残余应力的智能预测模型，与线性回归相比，该模型具有更高的精度;Umbrello等[16-17]针对轴承钢52100，结合FEM和人工神经网络(Artificial Neural Network, ANN)建立了一个切削残余应力的混合预测模型;Jafarian等[18]应用BP神经网络预测Inconel718半精车的残余应力，并采用遗传算法对切削速度、切削深度和进给率进行了优化。上述基于实验样本的统计模型适用范围狭窄，只能应用于指定工况，但在工程应用中却能起到立竿见影的效果。

本文针对球头刀的多轴铣削，以刀轴侧倾角、切削速度和每齿进给量为设计因子进行实验设计，开展铣削实验；然后应用径向基函数径向基函数(Radial Basis Function, RBF)神经网络预测已加工表面的残余应力，并与传统的线性回归经验模型及BP神经网络进行对比；最后分析了工艺参数对残余应力的交互影响规律。

1 铣削实验

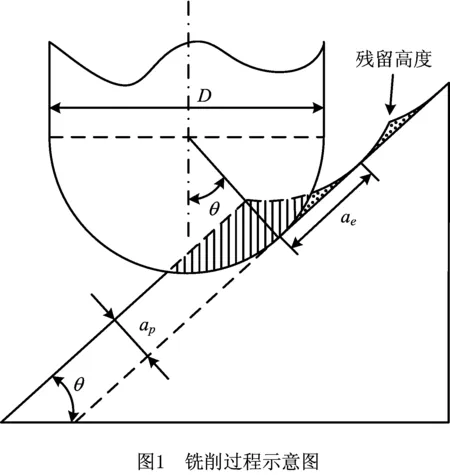
本文采用变倾角的斜面模拟航空发动机叶片的四轴精密铣削，如图1所示。工件材料为高温合金GH4169，共6块试件，其截面为梯形，高约70 mm，上底边长约30 mm，下底边因斜面倾角不同而有所不同，厚约37 mm，如图2所示;机床采用FVP-800A三坐标精密立式加工中心，铣削方式为逆铣，冷却方式为乳化液冷却。在航空发动机叶片实际生产中，改变铣削深度与铣削宽度相对比较困难，因此本文主要研究刀轴侧倾角、铣削速度和每齿进给量3个因子对铣削残余应力的影响，依据某型号叶片的工艺规范，固定铣削深度ap=0.2 mm，铣削宽度ag=0.3 mm。如图1所示，刀轴与加工表面法向之间的夹角θ为刀轴侧倾角。

为了减小刀具磨损对铣削残余应力的影响，每次实验均采用一把全新的刀具。球头铣刀所采用的材料与参数为：K44硬质合金，四齿，前角为6°，后角为10°，螺旋角为40°，直径为8 mm，总长110 mm，刃长12 mm，铣削实验时的刀具悬长76 mm。指定进给方向为x轴，y轴位于加工表面内并垂直于x轴。具体加工过程如图2所示。

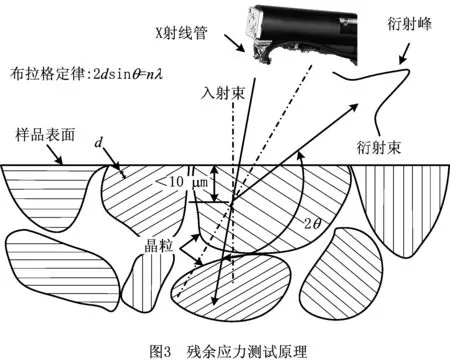
残余应力分为宏观应力、微观应力和晶内应力，本文仅针对宏观残余应力。图3所示为X射线衍射测试残余应力的原理：切削载荷导致工件表层多晶体材料的晶面间距d发生变化，基于布拉格定律，通过测量X射线的衍射角θ间接获得晶面间距d的变化，从而计算出晶格应变，最后利用胡克定律求得残余应力。

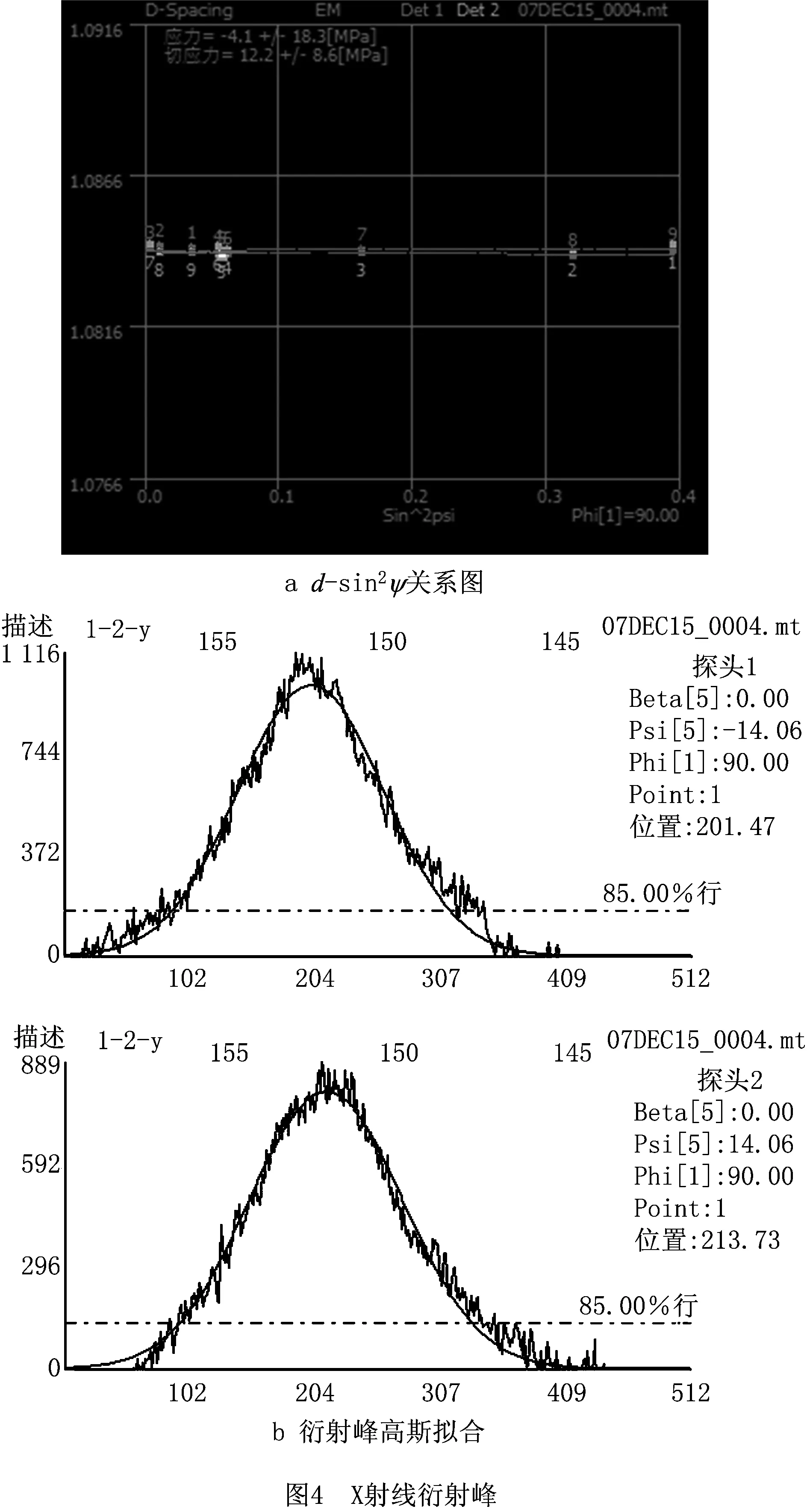
为了减小工件内部初始残余应力的影响，加工前先对工件进行热处理，以减小初始残余应力的影响。残余应力采用加拿大PROTO LXRD-MG2000 X射线衍射仪进行测试，测试处理后的表面残余应力的结果为σx=232.4±5.0 MPa，σy=133.7±5.4 MPa。为测试工件内部的初始残余应力，采用电解抛光仪对工件表面进行电解抛光，逐层测试测试残余应力直至残余应力趋近于零。当剥层深度为270 μm时，残余应力基本为零 (σx=-0.9±7.1 MPa，σy=-8.6±5.8 MPa)。图4所示为第一组实验y向残余应力的d-sin2ψ关系拟合效果及X射线衍射峰的高斯拟合效果。

热处理后工件表面有一层硬化层，并附带有一定初始残余应力，实验前先采用铣削方式去掉这一热硬化层，然而采用切削方式去除材料必然会重新引入切削残余应力，因此去掉热硬化层后，采用小切削深度(0.1 mm)预制待加工表面，以减小连续走刀对实验结果的影响。

针对航空发动机叶片的数控铣削，工艺参数的选取主要参考叶片实际生产中的工艺参数。设计变量共3个，分别为刀轴侧倾角θ角、切削速度v和每齿进给量fz。表1所示为工艺参数的变化范围及其水平设计，在参数域内每个因素取5水平。对于GH4169，过高的切削速度会迅速加剧刀具磨损，因此给定最大切削速度为80 m/min；依据工程经验，指定刀轴侧倾角在45°～85°之内，每齿进给量在0.01 mm/z～0.05 mm/z范围之内。

表1 工艺参数及其水平

采用正交实验设计方案L25(53)，共计25组实验。依据经验，采用神经网络建模，所需样本点为设计变量个数的10倍左右。另外，由正交实验方法可知，正交实验设计方案L25(53)的样本点大多位于设计空间的表面，内部实验点仅有4个(如图5)，较少的内部样本点可能使神经网络在设计空间内部区域的预测精度不足。因此在正交实验的基础上，进一步采用单因素实验，以[θ,v,fx]=[65°,50 m/min,0.03 mm/z]为对称中心均匀地增加设计空间中的内部样本量(如图5)，去掉重叠的实验点，共计35组实验。

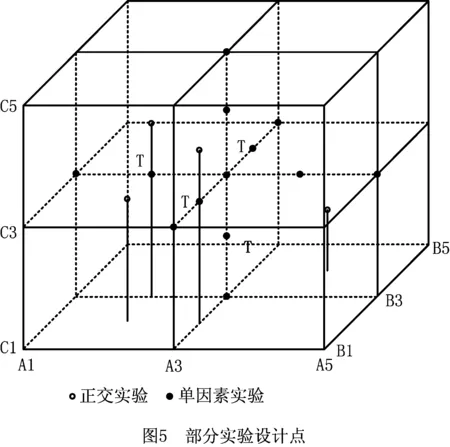
每组实验在不同位置测试两次残余应力，取均值作为实验结果。前31组实验作为训练样本，后4组用于测试，测试实验点用T进行了标识，如图5所示。表2所示为实验设计方案及相应的测试结果，其中负号表示残余应力为压应力。可以看出：测试结果大多为拉伸残余应力，仅有少量压缩残余应力，表明加工高温合金GH4169时，已加工表面更倾向于形成拉伸残余应力，这与GH4169航空叶片的实际加工经验相符，也凸显出对GH4169加工工艺进行优化的重要性；切削过程中，热载荷主要生成拉伸残余应力，而机械载荷是压缩残余应力的主要诱导因素；高切削温度是加工高温合金的一个典型特征，因此实验结果多为拉伸应力，然而通过改变刀具结构或切削用量，进而增强机械效应，则有望在已加工表面形成压应力。

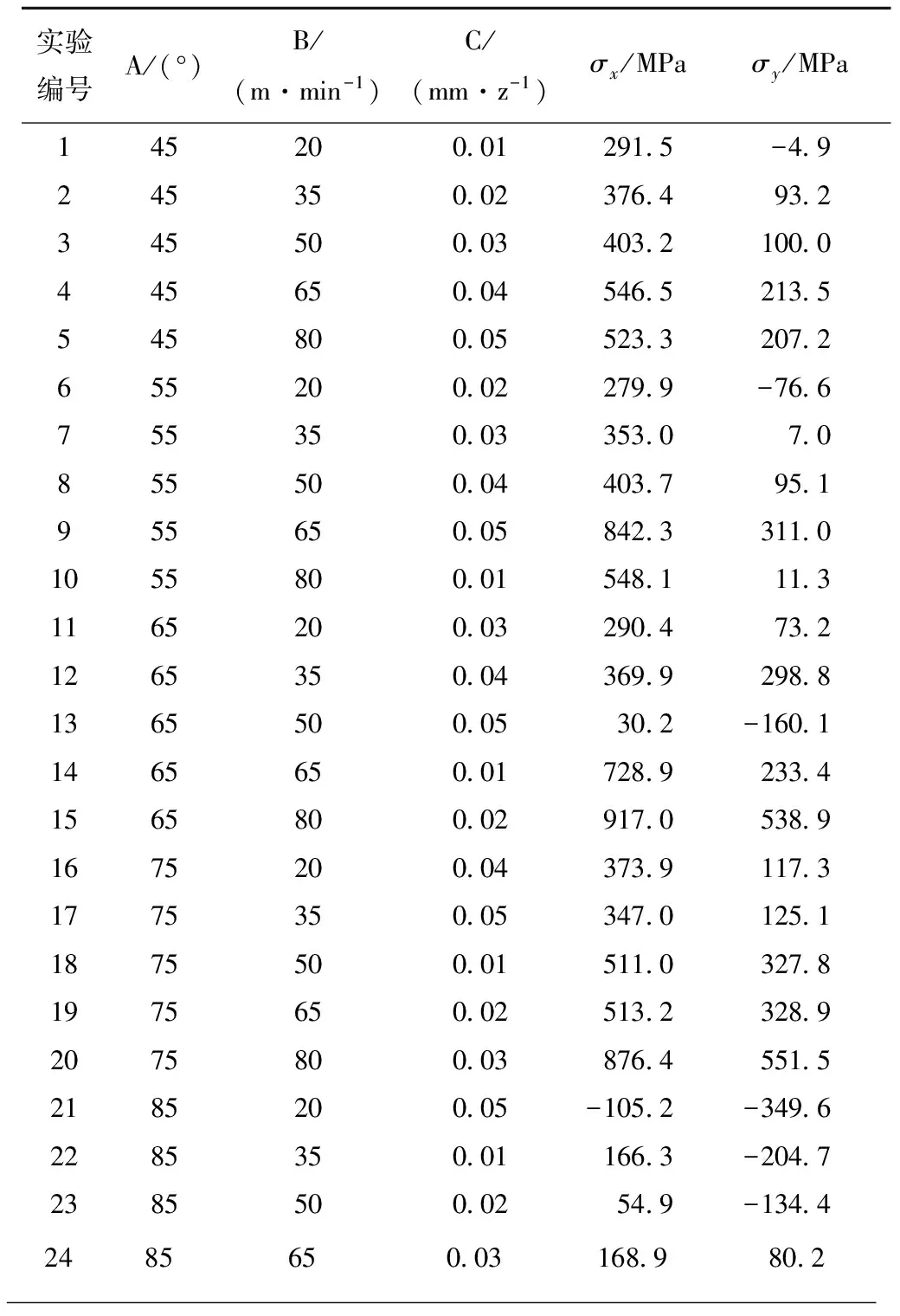
表2 实验设计与测试结果

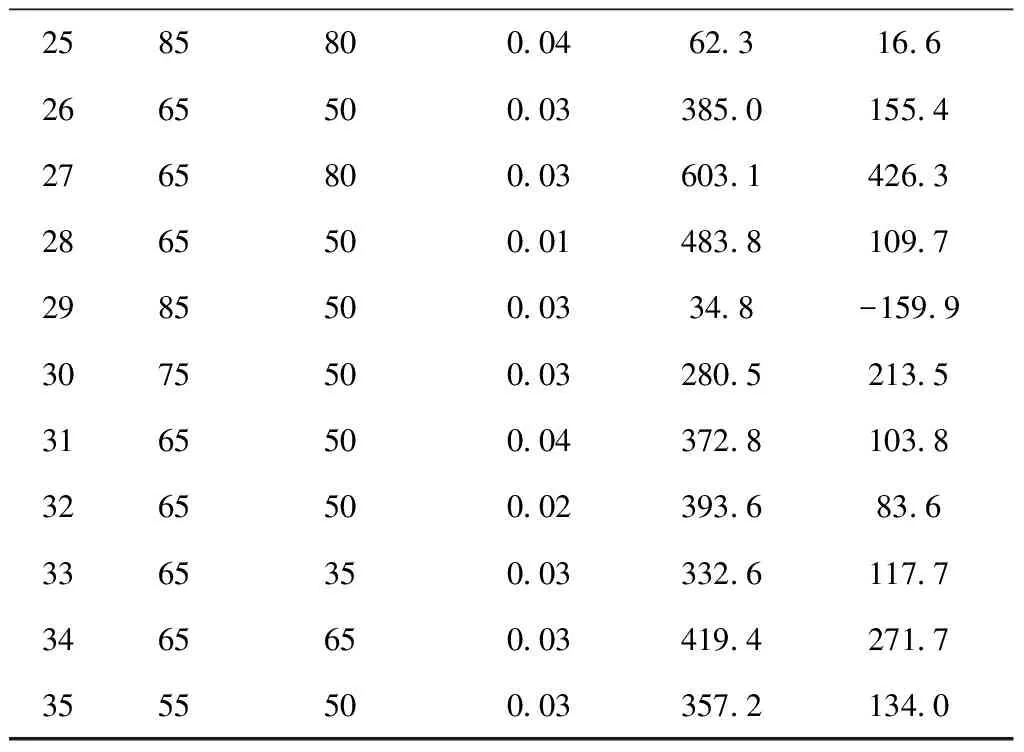
续表2

2 RBF神经网络

RBF(radial basis function)神经网络将学习的过程看作在高维空间中寻找一张能最佳拟合样本点的曲面，然后利用这张曲面对测试数据进行插值。1985年，Powell提出RBF方法来解决实多变量插值问题，随后该方法被Broomhead和Lowe(1988)应用于神经网络设计，形成RBF神经网络[19-20]。基本RBF网络结构包括输入层、隐含层和输出层3层。输入层由一些感知单元组成，连接网络与外界环境；RBF网络仅有一个隐含层，RBF作为“基”将输入矢量从输入空间非线性变换到隐含空间；网络的输出则是隐含单元的线性加权。根据Cover定理，将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的，因此隐含层往往有较高的维数，维数越高，逼近精度越高。

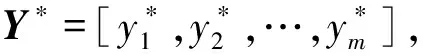
j=1,2,…,t,k=1,2,…,m。

(1)

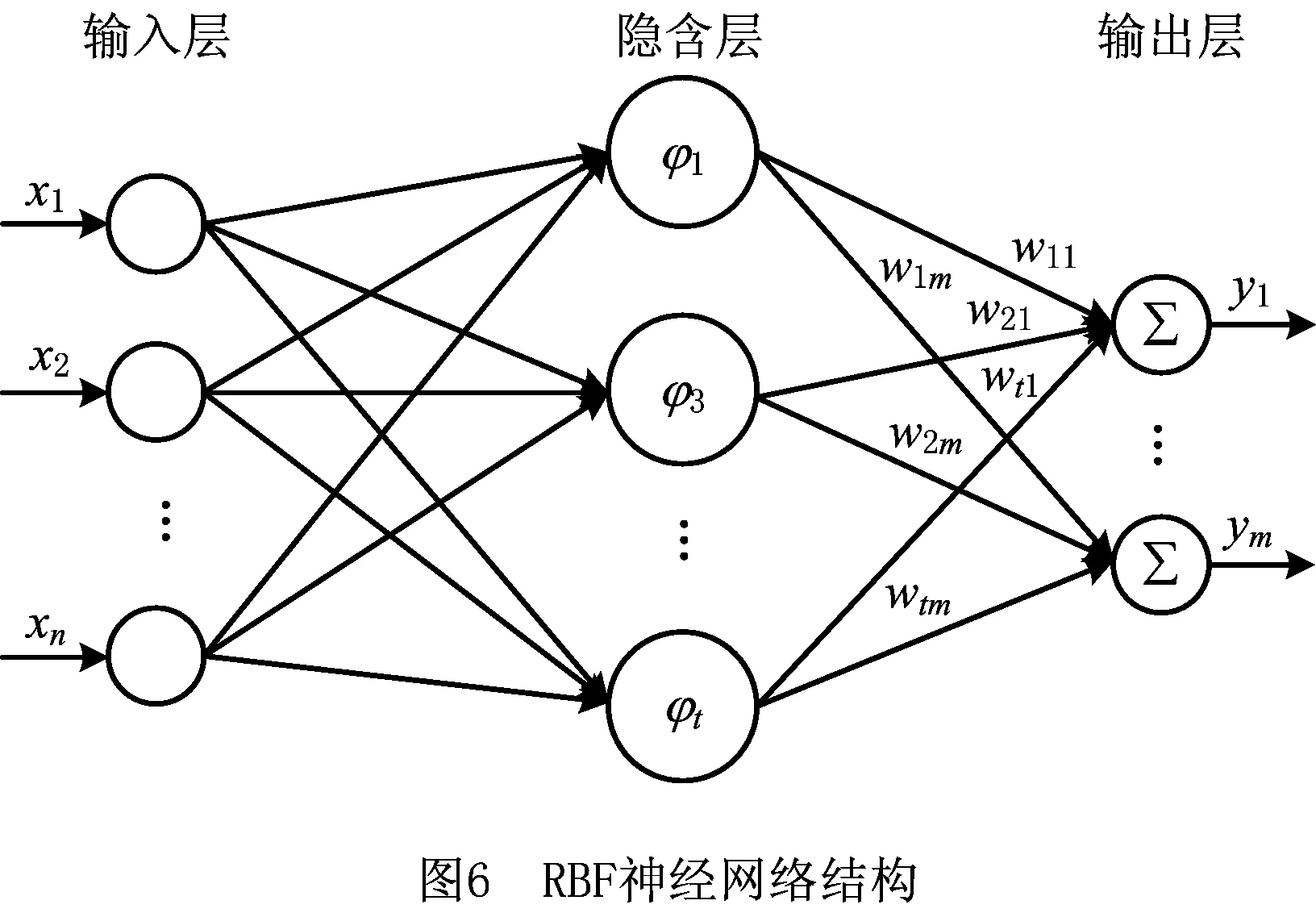
基函数对来自输入层的信号产生局部化的响应，一个隐含单元对应一个矢量c，将输入矢量与基函数中心矢量c进行比较，以产生径向对称的响应，而且仅当输入矢量落在中心邻域时，隐含单元才被激活并产生一个0～1之间的非零响应，输入矢量和中心的距离越小，该响应值越大。因此，基函数的中心选取对网络性能有十分重要的影响。RBF网络训练过程中仅有少数几个输出层的权值需要调整确定，与BP网络相比，RBF网络的学习速度有很大提高。考虑到高斯函数的表达形式简单，径向对称且光滑性良好，因此选用高斯函数作为基函数。

由于RBF神经网络具有上述结构特征，拥有最佳逼近和全局最优的性能，不易收敛于局部最优解，且网络训练需要调整的参数较少，使得这种训练高效而易行，因此RBF神经网络在解决非线性问题中得到了广泛应用。

3 基于RBF网络的铣削残余应力预测

3.1 RBF预测模型

铣削残余应力对工艺参数十分敏感，同时铣削本身又是一个高度非线性的大变形过程，理论上来说RBF神经网络适用于这一工程问题。

本文的3个输入变量分别为侧倾角θ、切削速度v和每齿进给量fz;输入矢量为x=[θ,v,fz]，三者的量纲不一致，因此对输入矢量按式(2)进行归一化处理。

(2)

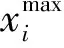
网络参数设置为：网络拟合误差目标值为0.001，扩展系数为0.22。通过MATLAB编程，建立RBF模型，采用前31组实验作为训练样本，对网络进行训练，获得最优的网络结构。对于两个方向的残余应力，隐含层单元数量均只需30个。图7所示为训练后的RBF神经网络在样本点的拟合值与实验值的对比，可以看出，RBF神经网络在实验点的拟合值几乎与实验结果完全重合，说明网络已经很好地完成了对样本点的最佳逼近。

为了测试所获得的RBF神经网络的泛化能力，采用后4组实验对网络模型进行测试，误差评价指标为

(3)

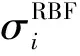
本文还分别采用BP神经网络与指数型经验模型对GH4169铣削残余应力进行预测，并与RBF神经网络预测模型进行对比。

(1)BP神经网络

基于测试实验，利用MATLAB软件建立铣削残余应力的BP神经网络模型。通过对网络调试，获得最佳的网络结构为3节点输入层、7节点隐含层、2节点输出层。

(2)指数型经验模型

假定铣削残余应力与工艺参数满足如下指数型关系：

(4)

对式(4)求对数，则

lg(σ-σ0)=lgk+algθ+blgv+clgfz。

(5)

为保证σ-σ0>0，对于σx，取σ0为-180；对于σy，取σ0为-390。采用MINITAB软件进行多元线性回归，获得残余应力的指数型经验公式为

(6)

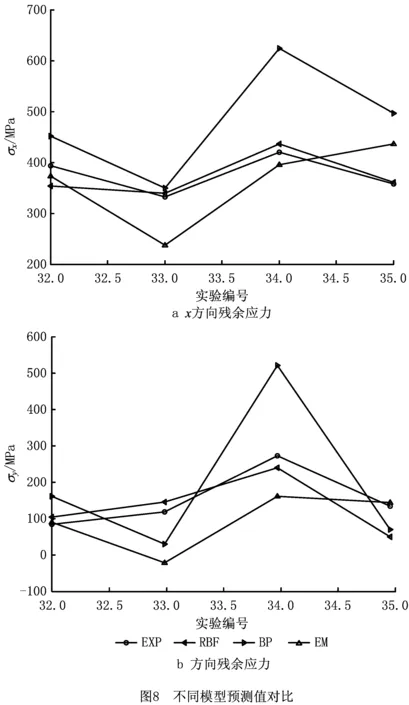
图8所示为不同模型预测结果的对比，可以看出，RBF神经网络的预测精度高于BP神经网络和指数型经验模型。对于残余应力σx，RBF神经网络的预测误差为5.89%，BP神经网络的预测误差为33.88%，指数型经验模型的预测误差为16.99%；对于残余应力σy，RBF神经网络的预测误差为31.96%，BP神经网络的预测误差为93.01%，指数型经验模型的预测误差为58.89%。可以看出，3种模型在y方向残余应力的预测误差相对较大。σy绝对值的平均值作为分母，仅为151.8 MPa，不到σx(375.7 MPa)的一半，而X射线测试残余应力的绝对误差最高可达±50 MPa，因此残余应力数值较小时相对误差就会较大。式(3)只是从总体上比较了各个模型的预测精度，在个别样本点处，RBF的预测误差可能偏大。例如第32组实验，RBF对两个方向残余应力的预测精度均略低于指数型经验公式;第35组实验，对于y方向残余应力，RBF的预测精度最低。然而，RBF预测模型具有最高的稳定性，BP预测模型和指数经验公式的预测误差则起伏不定。另外可以观察到，RBF预测模型的最大和最小绝对误差均出现在第35组实验，分别为Δσy=84.7 MPa与Δσx=3.6 MPa。

3.2 工艺参数对铣削残余应力的影响

切削是一种高度非线性的高温、大变形弹塑性行为，热-力耦合效应使材料的热关联属性呈非稳定状态，同时引起材料内部热应力-机械应力交替起伏，属于典型的材料非线性和几何非线性问题。切削过程中，刀具-工件的接触力学行为也处在时变状态，对工件表层材料内部的应力求解来说，其接触边界的时变特性使这一问题更为复杂，属典型的边界条件非线性问题。因此，工艺参数与切削响应之间的映射关系可能高度非线性，很难通过对实验数据序列进行简单变换就能获得线性映射(如指数公式)，这种非线性关系的表现形式之一，就是各工艺参数之间的交互项对切削特性有显著影响。3.1节表明，RBF神经网络能有效模拟铣削残余应力与侧倾角、切削速度和每齿进给量之间的这种非线性关系。

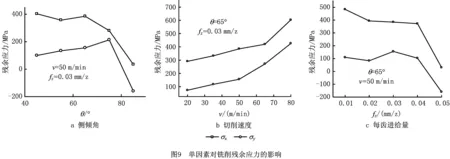
首先，采用单因素实验分析各个因子对铣削残余应力的影响趋势，如图9所示。可以看出，随着侧倾角的增加，σx整体呈下降趋势，而σy则先缓慢上升而后急剧下降，如图9a所示;切削热是引起已加工表面残余拉应力的主要原因，因此残余拉应力随切削速度的增加而增加，如图9b所示;随着每齿进给量的增加，两个方向的残余应力整体上均呈现下降趋势，并在fz=0.05 mm/z时获得y方向上的残余压应力，如图9c所示。由上述分析，容易得出最佳工艺参数水平组合为θ=85°，v=20 m/min，fz=0.05 mm/z,这样的结论并未考虑工艺参数之间的交互效应，因为铣削速度处在最低水平，所以材料去除率较低。

假定某叶片区域的刀轴侧倾角规划为70°，固定每齿进给量为0.05mm/z，按照上述规律，选择切削速度为20m/min可获得最小的残余应力。采用RBF模型计算出该参数组合下的残余应力分别为σx=232.8 MPa，σy=75.1 MPa，固定其他参数不变，通过RBF神经网络对切削速度寻优可以发现，当切削速度取56m/min时，获得的残余应力为σx=20.4 MPa，σy=-135.7 MPa，显然后者的切削效率更高，且获得了更小的残余应力，造成这种差异的原因是3个工艺因素之间存在一定的交互效应。

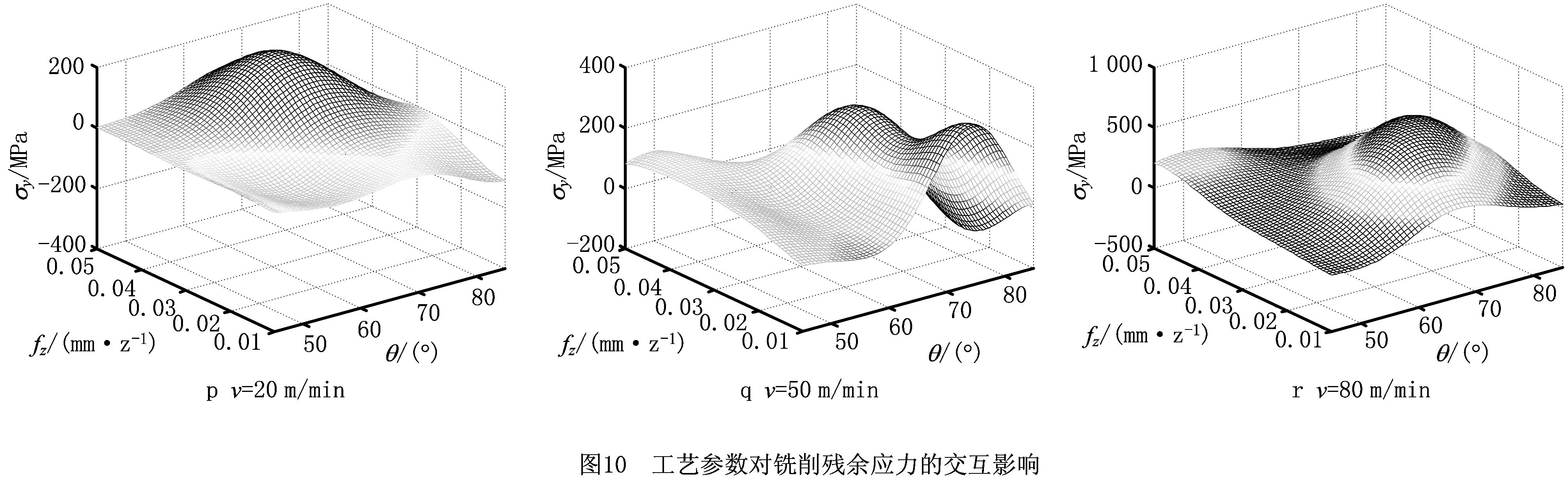
下面采用已获得的RBF模型分析这3个工艺参数对铣削残余应力的交互影响。在本文给定的参数域内，分别将侧倾角、切削速度和每齿进给量固定在高、中、低3个水平，然后采用RBF神经网络计算铣削残余应力，研究另外两个因素对残余应力的交互影响。图10所示为侧倾角、切削速度和每齿进给量对铣削残余应力σx与σy产生影响的三维曲面图。图10a～图10i所示为σx的三维响应图,图10j～图10r所示为σy的三维响应图。

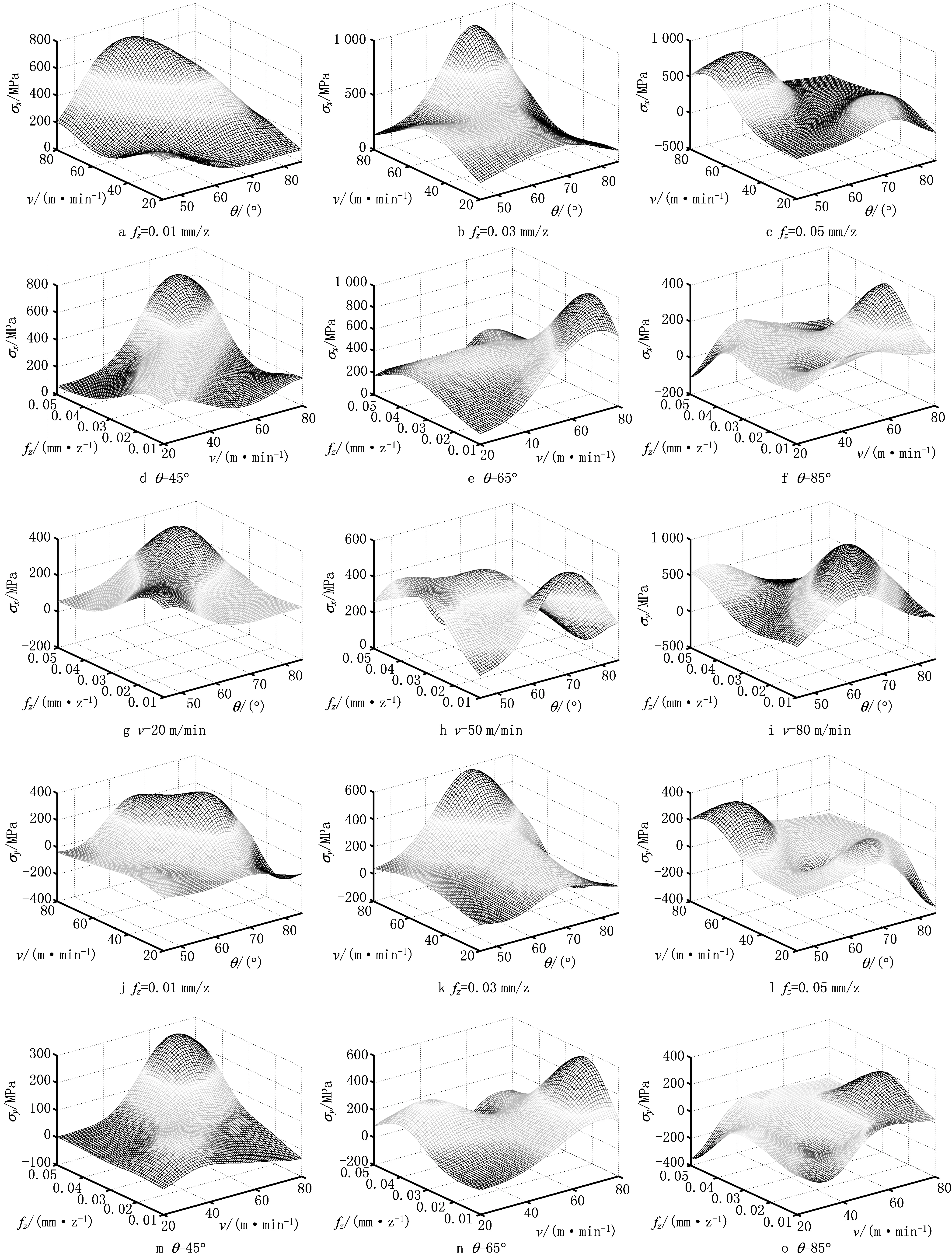
从图10a～图10c可以看出，残余应力σx的峰值一直位于最高切削速度区域，并向低侧倾角方向移动，随着每齿进给量的增加，残余应力峰值先上升而后降低。切削速度低于50 m/min时，拉应力较低，且当侧倾角等于85°时，拉应力最低。对比残余应力σy的三维响应曲面(如图10j～图10l)，曲面的形状非常相似，表明相近的规律同样适用于σy。整体上来说，残余应力曲面随每齿进给量的增加而先增后减。因此容易得出,当fz∈[0.01,0.05]mm/z时，低速、大侧倾角的铣削方式可以降低拉伸残余应力，有利于提高叶片加工表面的完整性。

图10d～图10f与图10m～图10o给出了每齿进给量与切削速度对σx和σy的交互影响，可见σx和σy的变化规律几乎完全一样。随着侧倾角由45°增加至85°，残余应力峰值由大进给率、高切削速度区域向低进给率方向移动，并且峰值均位于切削速度高于60 m/min的区域，同时最大残余应力先增后减，并在θ=85°时急剧降低，约为300 MPa左右，这时残余应力曲面整体下移，从而印证了大侧倾角有助于减小铣削残余应力。另外，低速、大进给可以获得较低的残余拉应力，尤其当侧倾角为85°时，在[fz,v]=[0.05 mm/z,20 m/min]邻域里获得了压缩的残余应力。

图10g～图10i与图10p～图10r描述了切削速度下铣削残余应力随每齿进给量与侧倾角变化的趋势。对于每齿进给量来说，残余应力峰值朝低参数区域方向移动；对于侧倾角来说，峰值位于θ=70°邻域的附近，因此在进行叶片铣削的刀轴规划时，要尽量选择较小或较大的刀轴侧倾角。对比不同切削速度下残余应力曲面的变化可以发现，随着切削速度的增加，残余应力整体上有十分显著的增加，由压应力向拉应力方向快速移动。

4 结束语

在当前国内倡导抗疲劳制造的背景下，研究典型航空材料加工表面完整性的工程应用价值显得尤为突出。目前，GH4169多轴球头铣削产生的残余应力仍然没有被很好地理解，因此本文提出一个GH4169航空叶片多轴铣削的RBF预测模型，为下一步工艺参数优化奠定了理论基础。具体结论如下：

(1)铣削残余应力与刀轴侧倾角、铣削速度及每齿进给量存在强非线性关系，并且3个工艺因子对两个方向残余应力的交互效应十分相似。

(2)RBF神经网络能有效地模拟铣削残余应力与刀轴侧倾角、铣削速度及每齿进给量之间的非线性映射关系，具有较高的预测精度并优于传统的BP神经网络和指数型经验模型。

(3)球头刀铣削高温合金GH4169时，在[45°,85°]参数域内，侧倾角的优选顺序为高水平、低水平、中间值。

[1] ZHANG Jingying, LIANG S Y, ZHANG Guowei, et al. Modeling of residual stress profile in finish hard turning[J]. Materials and Manufacturing Processes, 2006,21(1):39-45.

[2] NASR M, NG E G, ELBESTAWI M. Effects of workpiece thermal properties on machining-induced residual stresses-thermal softening and conductivity[J]. Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture, 2007,221(9):1387-1400.

[3] FUH K H, WU C F.A residual-stressmodel for the milling of aluminum alloy(2014-T6)[J].Journal of Materials Processing Technology, 1995,51(1/2/3/4):87-106.

[4] NAVAS V G, GONZALO O, BENGOETXEA I. Effect of cutting parameters in the surface residual stresses generated by turning in AISI 4340 steel[J]. International Journal of Machine Tools and Manufacture, 2012,61(4):48-57.

[5] MASMIATI N, SARHAN A A D. Optimizing cutting parameters in inclined end milling for minimum surface residual stress-Taguchi approach[J]. Measurement, 2015,60:267-275.

[6] LIANG Yuesheng, SU J C. Residual stress modeling in orthogonal machining[J]. CIRP Annals-Manufacturing Technology, 2007, 56(1):65-68.

[7] ULUTAN D, ALACA B E, LAZOGLU I. Analytical modelling of residual stresses in machining[J]. Journal of Materials Processing Technology, 2007,183(1):77-87.

[8] SU J C, YOUNG K A, MA K, et al.Modeling of residual stresses in milling[J]. International Journal of Advanced Manufacturing Technology, 2013, 65(5/6/7/8):717-733.

[9] ÖZEL T, ULUTAN D. Prediction of machining induced residual stresses in turning of titanium and nickel based alloys with experiments and finite element simulations[J].CIRP Annals-Manufacturing Technology, 2012,61(1):547-550.

[10] VALIORGUE F, RECH J, HAMDI H, et al. A new approach for the modelling of residual stresses induced by turning of 316L[J]. Journal of Materials Processing Technology, 2007,191(1):270-273.

[11] MONDELIN A, VALIORGUE F, RECH J, et al. Hybrid model for the prediction of residual stresses induced by 15-5PH steel turning[J]. International Journal of Mechanical Sciences, 2012,58(1):69-85.

[12] VALIORGUE F, RECH J, HAMDI H, et al. 3D modeling of residual stresses induced in finish turning of an AISI304L stainless steel[J]. International Journal of Machine Tools and Manufacture, 2012,53(1):77-90.

[13] SAINI S, AHUJA I S, SHARMA V S. Residual stresses, surface roughness, and tool wear in hard turning:a comprehensive review[J]. Materials and Manufacturing Processes, 2012,27(6):583-598.

[14] SAINI S, AHUJA I S, SHARMA V S. Modelling the effects of cutting parameters on residual stresses in hard turning of AISI H11 tool steel[J]. The International Journal of Advanced Manufacturing Technology, 2012,65(5/6/7/8):667-678.

[15] AXIR M H E. A method of modeling residual stress distribution in turning for different materials[J]. International Journal of Machine Tools and Manufacture,2002,42(9):1055-1064.

[16] UMBRELLO D, AMBROGIO G, FILICE L, et al. An ANN approach for predicting subsurface residual stresses and the desired cutting conditions during hard turning[J]. Journal of Materials Processing Technology, 2007,189(1):143-152.

[17] UMBRELLO D, AMBROGIO G, FILICE L, et al.A hybrid finite element method-artificial neural network approach for predicting residual stresses and the optimal cutting conditions during hard turning of AISI 52100 bearing steel[J]. Materials & Design, 2008,29(4):873-883.

[18] JAFARIAN F, AMIRABADI H, SADRI J. Experimental measurement and optimization of tensile residual stress in turning process of Inconel718 superalloy[J]. Measurement, 2015,63:1-10.

[19] BROOMHEAD D S, LOWE D. Radial basis functions, multi-variable functional interpolation and adaptive networks[J]. Advances in Neural Information Processing Systems,1988,4148:728-734.

[20] HAYKIN S. Neural networks[M]. Beijing:China Machine Press, 2004:183-224(in Chinese).[Haykin S.神经网络原理[M].北京:机械工业出版社，2004:183-224.]